沪教版(上海)数学高三上册-15.4几何体的表面积 (教案)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.4几何体的表面积 (教案) |

|
|
| 格式 | doc | ||
| 文件大小 | 116.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:40:06 | ||
图片预览

文档简介
几何体的表面积
【教学目标】
1.知识与技能
(1)通过对柱、锥、台体的研究,掌握柱、锥、台的表面积的求法。
(2)能运用公式求解,柱体、锥体和台全的全面积,并且熟悉台体与体和锥体之间的转换关系。
(3)培养学生空间想象能力和思维能力。
2.过程与方法
(1)让学生经历几何全的侧面展一过程,感知几何体的形状。
(2)让学生通对照比较,理顺柱体、锥体、台体三间的面积的关系。
3.情感与价值
通过学习,使学生感受到几何体面积的求解过程,对自己空间思维能力影响。从而增强学习的积极性。
【教学重难点】
重点:柱体、锥体、台体的表面积计算。
难点:台体表面积公式的推导
【教学过程】
一、引例
在初中已经学过正方体和长方体的表面积,你知道正方体和长方体的展开图的面积与其表面积的关系吗?
多面体是由一些平面多边形围成的几何体,沿着多面体的某些棱将它剪开,各个面就可展开在一个平面内,得到一个平面图形,这个平面图形叫做该多面体的平面展开图。
二、问题。
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
正六棱柱的侧面展开图是什么?如何计算它的表面积?
正五棱锥的侧面展开图是什么?如何计算它的表面积
正四棱台的侧面展开图是什么?如何计算它的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和。
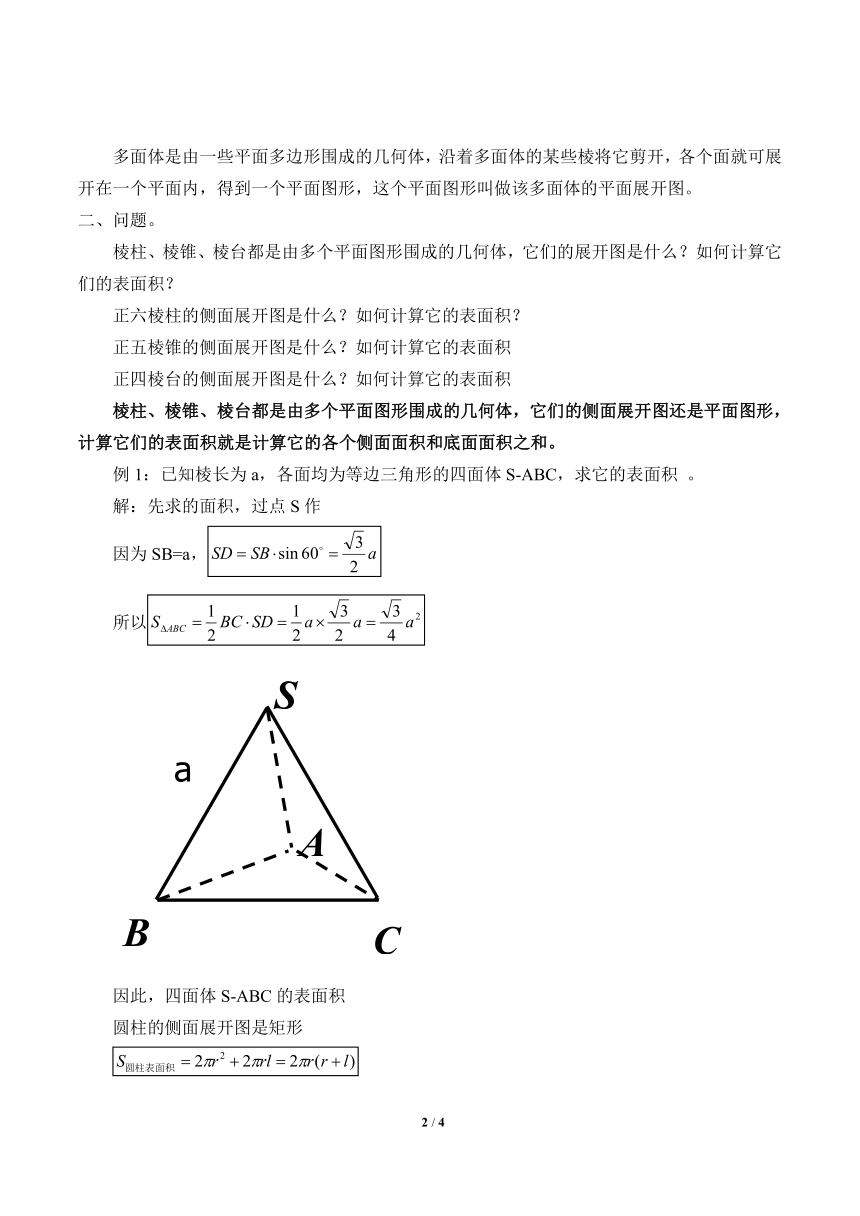
例1:已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积
。
解:先求的面积,过点S作
因为SB=a,
所以
因此,四面体S-ABC的表面积
圆柱的侧面展开图是矩形
圆锥的侧面展开图是扇形
圆台的侧面展开图是扇环
例2:如图,一个圆台形花盆盆口直径20
cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm。那么花盆的表面积约是多少平方厘米(取3.14,结果精确到1)?
解:由圆台的表面积公式得
花盆的表面积:
答:花盆的表面积约是999
三、小结
圆柱
柱体、锥体、台体的表面积
圆台
圆锥
1.有一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积为:
A.24πcm2
B.15πcm2,
C.26πcm2,
D.以上都不正确
2.棱长都是1的三棱锥的表面积为(
)
A.
B.2
C.3
D.4
3.将圆心角为1200,面积为3的扇形,作为圆锥的侧面,求圆锥的表面积?
4.已知圆锥的表面积为a
㎡,且它的侧面展开图是一个半圆,则这个圆锥的底面直径为
。
参考答案
1.A
2.A;
3.解:l=3,R=1;S=4;
4.
B
C
A
S
a
展开图
各面面积之和
6
5
1
/
1
【教学目标】
1.知识与技能
(1)通过对柱、锥、台体的研究,掌握柱、锥、台的表面积的求法。
(2)能运用公式求解,柱体、锥体和台全的全面积,并且熟悉台体与体和锥体之间的转换关系。
(3)培养学生空间想象能力和思维能力。
2.过程与方法
(1)让学生经历几何全的侧面展一过程,感知几何体的形状。
(2)让学生通对照比较,理顺柱体、锥体、台体三间的面积的关系。
3.情感与价值
通过学习,使学生感受到几何体面积的求解过程,对自己空间思维能力影响。从而增强学习的积极性。
【教学重难点】
重点:柱体、锥体、台体的表面积计算。
难点:台体表面积公式的推导
【教学过程】
一、引例
在初中已经学过正方体和长方体的表面积,你知道正方体和长方体的展开图的面积与其表面积的关系吗?
多面体是由一些平面多边形围成的几何体,沿着多面体的某些棱将它剪开,各个面就可展开在一个平面内,得到一个平面图形,这个平面图形叫做该多面体的平面展开图。
二、问题。
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
正六棱柱的侧面展开图是什么?如何计算它的表面积?
正五棱锥的侧面展开图是什么?如何计算它的表面积
正四棱台的侧面展开图是什么?如何计算它的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和。
例1:已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积
。
解:先求的面积,过点S作
因为SB=a,
所以
因此,四面体S-ABC的表面积
圆柱的侧面展开图是矩形
圆锥的侧面展开图是扇形
圆台的侧面展开图是扇环
例2:如图,一个圆台形花盆盆口直径20
cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm。那么花盆的表面积约是多少平方厘米(取3.14,结果精确到1)?
解:由圆台的表面积公式得
花盆的表面积:
答:花盆的表面积约是999
三、小结
圆柱
柱体、锥体、台体的表面积
圆台
圆锥
1.有一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积为:
A.24πcm2
B.15πcm2,
C.26πcm2,
D.以上都不正确
2.棱长都是1的三棱锥的表面积为(
)
A.
B.2
C.3
D.4
3.将圆心角为1200,面积为3的扇形,作为圆锥的侧面,求圆锥的表面积?
4.已知圆锥的表面积为a
㎡,且它的侧面展开图是一个半圆,则这个圆锥的底面直径为
。
参考答案
1.A
2.A;
3.解:l=3,R=1;S=4;
4.
B
C
A
S
a
展开图
各面面积之和
6
5
1
/
1
