沪教版(上海)数学高三上册-14.3 空间直线与平面的位置关系 (课件)(共29张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-14.3 空间直线与平面的位置关系 (课件)(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 787.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:39:26 | ||
图片预览




文档简介
(共29张PPT)
空间直线与平面的位置关系
复习旧知
1.
简述空间两条不重合直线间的位置关系.
相交
平行
异面
复习旧知
2.
由直线与平面的公共点的个数总结直线与平面间的不同位置关系:
→直线与平面相交
→直线与平面平行
→直线在平面上
1个公共点
2个公共点
0个公共点
(无数个)
复习旧知
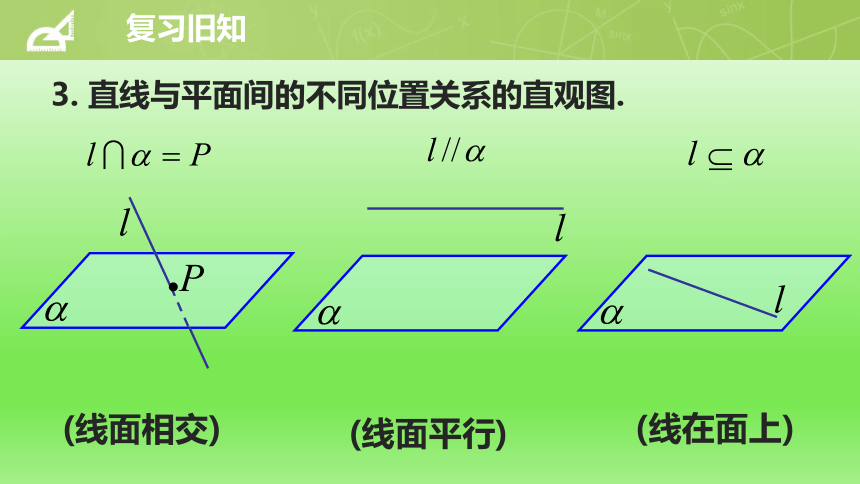
3.
直线与平面间的不同位置关系的直观图.
(线面相交)
(线面平行)
(线在面上)
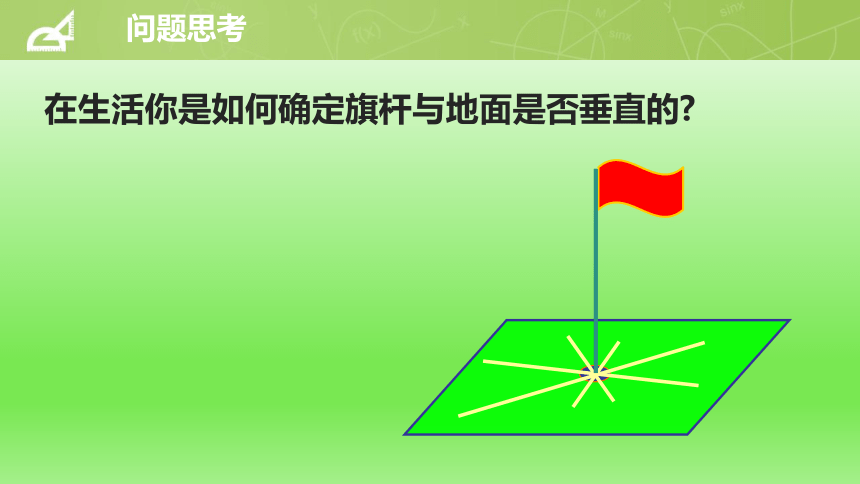
问题思考
在生活你是如何确定旗杆与地面是否垂直的
知识讲解
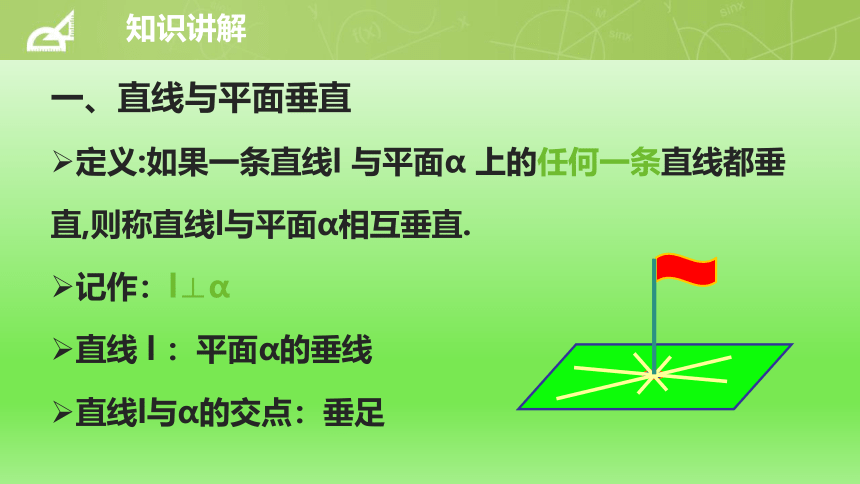
一、直线与平面垂直
定义:如果一条直线l
与平面α
上的任何一条直线都垂
直,则称直线l与平面α相互垂直.
记作:l⊥α
直线
l
:平面α的垂线
直线l与α的交点:垂足
知识讲解
一、直线与平面垂直
定义:如果一条直线l
与平面α
上的任何一条直线都垂
直,则称直线l与平面α相互垂直.
说明:判断线与线的垂直关系:
线面垂直
线线垂直
知识讲解
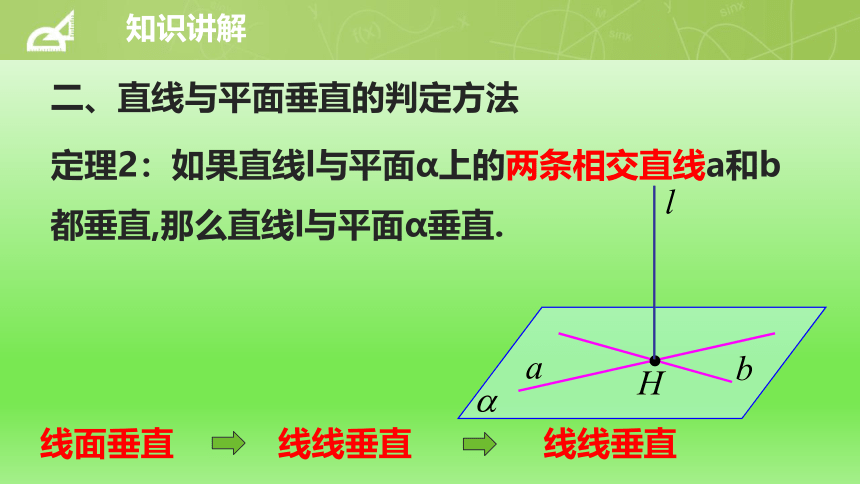
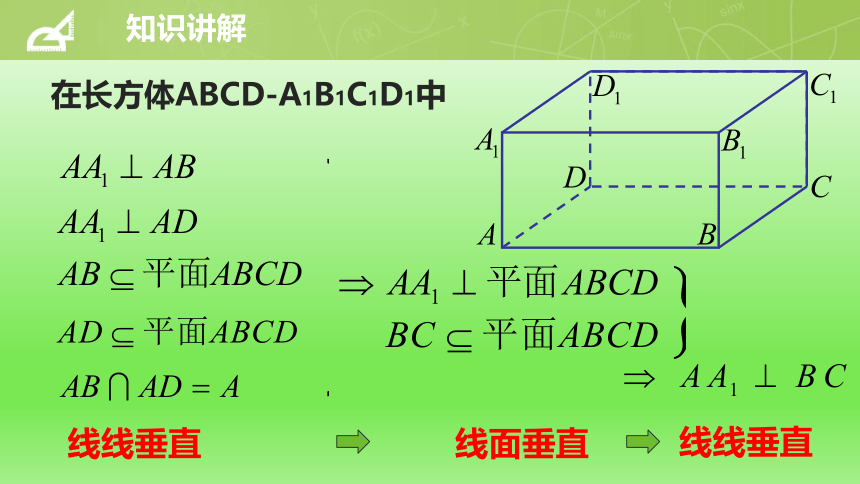
二、直线与平面垂直的判定方法
定理2:如果直线l与平面α上的两条相交直线a和b都垂直,那么直线l与平面α垂直.
线面垂直
线线垂直
线线垂直
知识讲解
在长方体ABCD-A1B1C1D1中
线面垂直
线线垂直
线线垂直
知识讲解
三、空间图形中有关的距离的定义
①点M和平面α的距离:M是平面α外一点;
过点M作平面α的垂线,垂足为N;
MN:点M和平面α的距离.
知识讲解
三、空间图形中有关的距离的定义
②直线
l
和平面α的距离:
l
∥
平面α;
l上任取点M;
线段MN:直线
l和平面α的距离.
知识讲解
三、空间图形中有关的距离的定义
③平面α和平面β的距离:
α
∥β
α上任取点M;
线段MN:直线
l和平面α的距离.
知识讲解
三、空间图形中有关的距离的定义
④异面直线a和b的距离:a、b是异面直线,
点M、N分别在a和b上;
MN⊥a
且MN⊥b;
直线MN:a和b的公垂线;
线段MN:a和b的距离.
例1
已知长方体ABCD-A'B'C'D'的棱长AA'、AB
和AD的长分别为3cm、4cm和5cm.
(1)求点A和点C'的距离;
(2)求点A到棱B'C'的距离;
(3)求棱AB和平面A'B'C'D'的距离;
(4)求异面直线AD和A'B'的距离.
例题讲解
判断证明
计算求距
如果直线和平面不垂直,
此时又该如何刻画直线
和平面的这种关系呢
问题思考
四、直线与平面的夹角
平面的斜线:
直线PA和平面α相交,但不垂直
这条直线叫做该平面的斜线
斜线和平面的交点A叫做斜足.
知识讲解
P
A
斜足
斜线
斜线
斜足
射影
垂足
垂线
知识讲解
2.直线与平面所成的角
过斜线上斜足以外的一点向平面引垂线PO
斜线在平面上的射影:直线AO
直线与平面所成的角:
斜线与平面上的射影所成锐角
知识讲解
2.直线与平面所成的角
规定:
一条直线垂直于平面,我们说它所成的角是直角
一条直线平行于平面,或在平面内,我们说它所成
的角是00的角.
思考:
直线与平面所成的角θ的取值范围是什么
巩固练习
1.判断下列说法是否正确
①两平行直线在同一平面内的射影一定是平行直线
②两相交直线在同一平面内的射影一定是相交直线
③两异面直线在同一平面内的射影要么是平行直线,要么是相交直线
④若斜线段长相等,则它们在平面内的射影长相等
×
×
×
×
例2
如图,在正方体ABCD-A1B1C1D1的棱长为a
①求A1B和平面ABCD所成的角
②求D1B和平面ABCD所成的角
例题讲解
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
A1
D1
C1
B1
A
D
C
B
O
线段B1O
巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(2)AB1在面A1B1CD中的射影
E
线段B1E
巩固练习
A1
D1
C1
B1
A
D
C
B
2.如图:正方体ABCD-A1B1C1D1中,求:
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
线段C1D
巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
A1
D1
C1
B1
A
D
C
B
0o
巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(2)
A1C1与面BB1D1D所成的角
A1
D1
C1
B1
A
D
C
B
90o
巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(3)
A1C1与面BB1C1C所成的角
A1
D1
C1
B1
A
D
C
B
45o
巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
E
30o
巩固练习
例3
已知平面与平面相互平行,平面与它们的交线
分别为a、b,求证:a∥b
例题讲解
知识总结
1.
空间直线与平面垂直的定义及判定:定理2
2.
空间图形中有关的距离的定义:点、直线、面
3.
直线与平面所成的角:斜线、射影
判断证明
计算求距
空间直线与平面的位置关系
复习旧知
1.
简述空间两条不重合直线间的位置关系.
相交
平行
异面
复习旧知
2.
由直线与平面的公共点的个数总结直线与平面间的不同位置关系:
→直线与平面相交
→直线与平面平行
→直线在平面上
1个公共点
2个公共点
0个公共点
(无数个)
复习旧知
3.
直线与平面间的不同位置关系的直观图.
(线面相交)
(线面平行)
(线在面上)
问题思考
在生活你是如何确定旗杆与地面是否垂直的
知识讲解
一、直线与平面垂直
定义:如果一条直线l
与平面α
上的任何一条直线都垂
直,则称直线l与平面α相互垂直.
记作:l⊥α
直线
l
:平面α的垂线
直线l与α的交点:垂足
知识讲解
一、直线与平面垂直
定义:如果一条直线l
与平面α
上的任何一条直线都垂
直,则称直线l与平面α相互垂直.
说明:判断线与线的垂直关系:
线面垂直
线线垂直
知识讲解
二、直线与平面垂直的判定方法
定理2:如果直线l与平面α上的两条相交直线a和b都垂直,那么直线l与平面α垂直.
线面垂直
线线垂直
线线垂直
知识讲解
在长方体ABCD-A1B1C1D1中
线面垂直
线线垂直
线线垂直
知识讲解
三、空间图形中有关的距离的定义
①点M和平面α的距离:M是平面α外一点;
过点M作平面α的垂线,垂足为N;
MN:点M和平面α的距离.
知识讲解
三、空间图形中有关的距离的定义
②直线
l
和平面α的距离:
l
∥
平面α;
l上任取点M;
线段MN:直线
l和平面α的距离.
知识讲解
三、空间图形中有关的距离的定义
③平面α和平面β的距离:
α
∥β
α上任取点M;
线段MN:直线
l和平面α的距离.
知识讲解
三、空间图形中有关的距离的定义
④异面直线a和b的距离:a、b是异面直线,
点M、N分别在a和b上;
MN⊥a
且MN⊥b;
直线MN:a和b的公垂线;
线段MN:a和b的距离.
例1
已知长方体ABCD-A'B'C'D'的棱长AA'、AB
和AD的长分别为3cm、4cm和5cm.
(1)求点A和点C'的距离;
(2)求点A到棱B'C'的距离;
(3)求棱AB和平面A'B'C'D'的距离;
(4)求异面直线AD和A'B'的距离.
例题讲解
判断证明
计算求距
如果直线和平面不垂直,
此时又该如何刻画直线
和平面的这种关系呢
问题思考
四、直线与平面的夹角
平面的斜线:
直线PA和平面α相交,但不垂直
这条直线叫做该平面的斜线
斜线和平面的交点A叫做斜足.
知识讲解
P
A
斜足
斜线
斜线
斜足
射影
垂足
垂线
知识讲解
2.直线与平面所成的角
过斜线上斜足以外的一点向平面引垂线PO
斜线在平面上的射影:直线AO
直线与平面所成的角:
斜线与平面上的射影所成锐角
知识讲解
2.直线与平面所成的角
规定:
一条直线垂直于平面,我们说它所成的角是直角
一条直线平行于平面,或在平面内,我们说它所成
的角是00的角.
思考:
直线与平面所成的角θ的取值范围是什么
巩固练习
1.判断下列说法是否正确
①两平行直线在同一平面内的射影一定是平行直线
②两相交直线在同一平面内的射影一定是相交直线
③两异面直线在同一平面内的射影要么是平行直线,要么是相交直线
④若斜线段长相等,则它们在平面内的射影长相等
×
×
×
×
例2
如图,在正方体ABCD-A1B1C1D1的棱长为a
①求A1B和平面ABCD所成的角
②求D1B和平面ABCD所成的角
例题讲解
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
A1
D1
C1
B1
A
D
C
B
O
线段B1O
巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(2)AB1在面A1B1CD中的射影
E
线段B1E
巩固练习
A1
D1
C1
B1
A
D
C
B
2.如图:正方体ABCD-A1B1C1D1中,求:
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
线段C1D
巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
A1
D1
C1
B1
A
D
C
B
0o
巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(2)
A1C1与面BB1D1D所成的角
A1
D1
C1
B1
A
D
C
B
90o
巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(3)
A1C1与面BB1C1C所成的角
A1
D1
C1
B1
A
D
C
B
45o
巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
E
30o
巩固练习
例3
已知平面与平面相互平行,平面与它们的交线
分别为a、b,求证:a∥b
例题讲解
知识总结
1.
空间直线与平面垂直的定义及判定:定理2
2.
空间图形中有关的距离的定义:点、直线、面
3.
直线与平面所成的角:斜线、射影
判断证明
计算求距
