沪教版(上海)数学高三上册-第14章 空间直线与平面 复习(课件)(共38张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-第14章 空间直线与平面 复习(课件)(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 00:00:00 | ||
图片预览





文档简介
(共38张PPT)
第14章
空间直线与平面
复习课件
知识梳理
达标检测
题型探究
内容索引
知识梳理
1.四个公理
公理1:如果一条直线上的
在一个平面内,那么这条直线上所有的点都在这个平面内.
公理2:过
的三点,有且只有一个平面.
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有
.
公理4:平行于同一条直线的两条直线互相
.
两点
不在同一条直线上
一条过该点的公共直线
平行
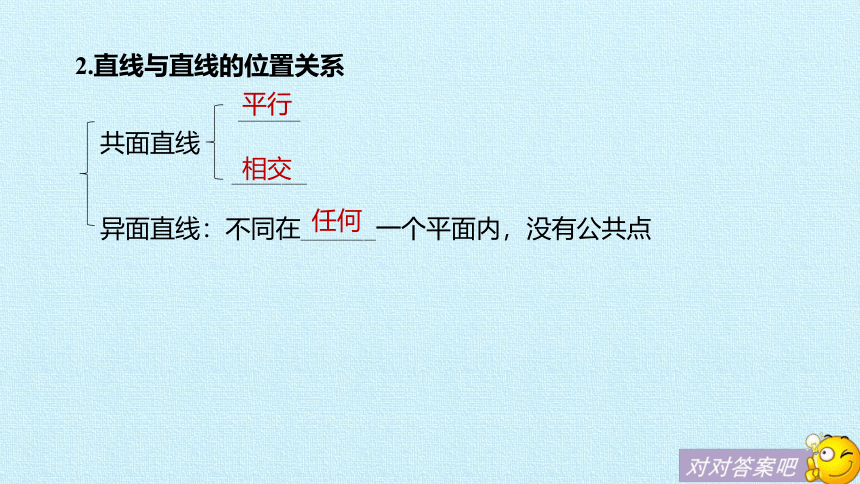
2.直线与直线的位置关系
_____
共面直线
______
异面直线:不同在______一个平面内,没有公共点
平行
任何
相交
判定
性质
定义
定理
图形
条件
________
___________
______
_______
____________
________
结论
a∥α
b∥α
a∩α=
a∥b
3.平行的判定与性质
(1)直线与平面平行的判定与性质
a∩α=
a α,b α,
a∥b
a∥α,a β,
α∩β=b
a∥α
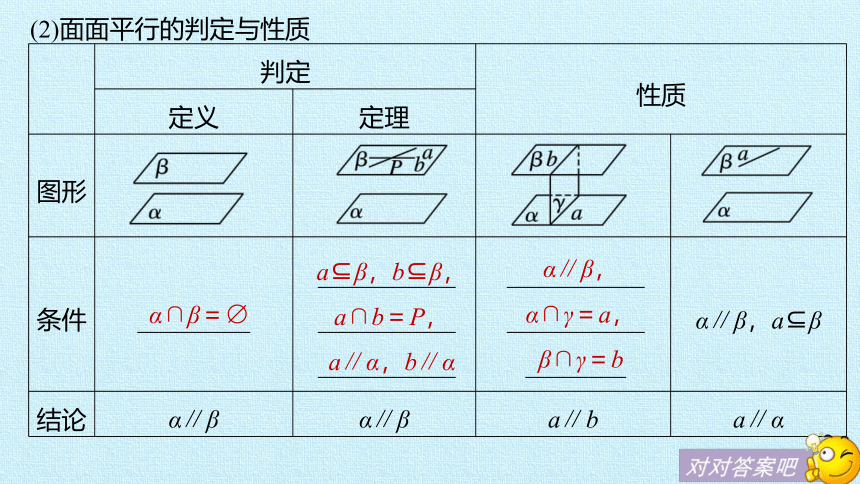
(2)面面平行的判定与性质
α∩β=
判定
性质
定义
定理
图形
条件
_________
___________
___________
___________
___________
___________
________
α∥β,a β
结论
α∥β
α∥β
a∥b
a∥α
a β,b β,
a∩b=P,
a∥α,b∥α
α∥β,
α∩γ=a,
β∩γ=b
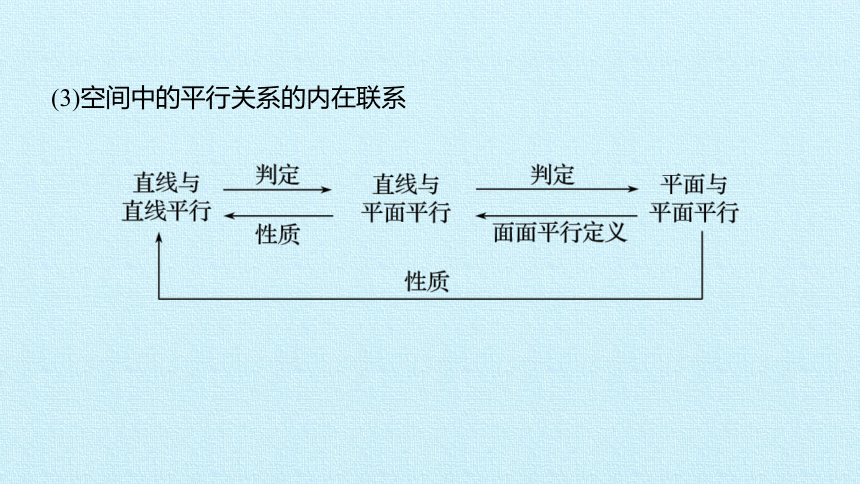
(3)空间中的平行关系的内在联系
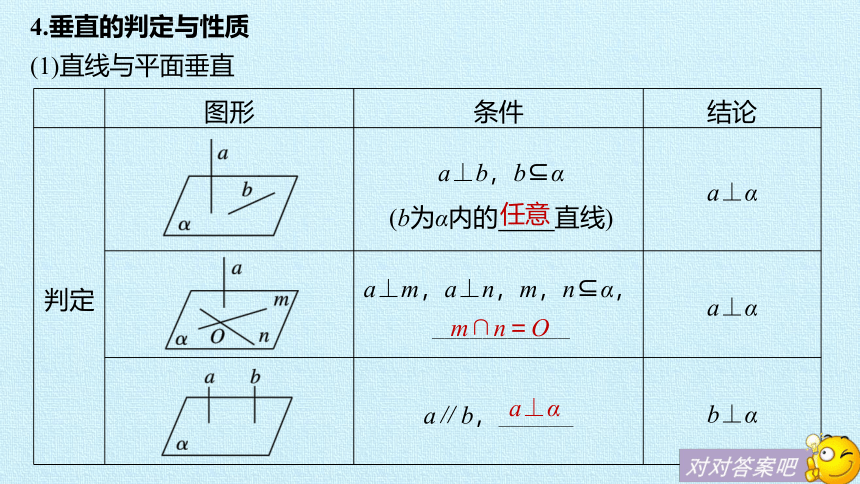
4.垂直的判定与性质
(1)直线与平面垂直
任意
图形
条件
结论
判定
a⊥b,b α
(b为α内的
直线)
a⊥α
a⊥m,a⊥n,m,n α,
___________
a⊥α
a∥b,______
b⊥α
m∩n=O
a⊥α
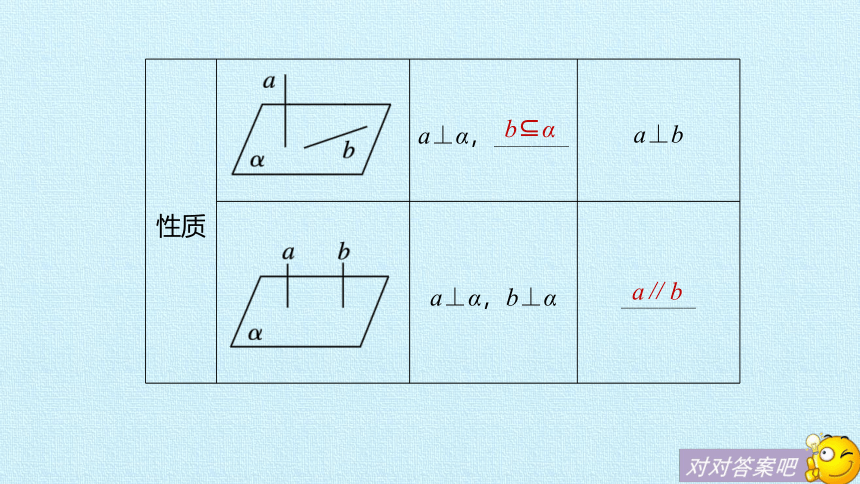
性质
a⊥α,______
a⊥b
a⊥α,b⊥α
______
b α
a∥b
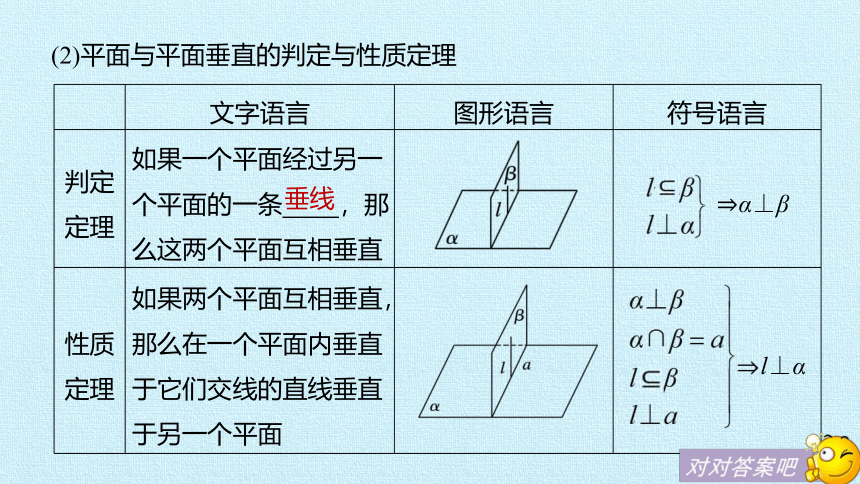
(2)平面与平面垂直的判定与性质定理
文字语言
图形语言
符号语言
判定
定理
如果一个平面经过另一个平面的一条
,那么这两个平面互相垂直
α⊥β
性质
定理
如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面
l⊥α
垂线
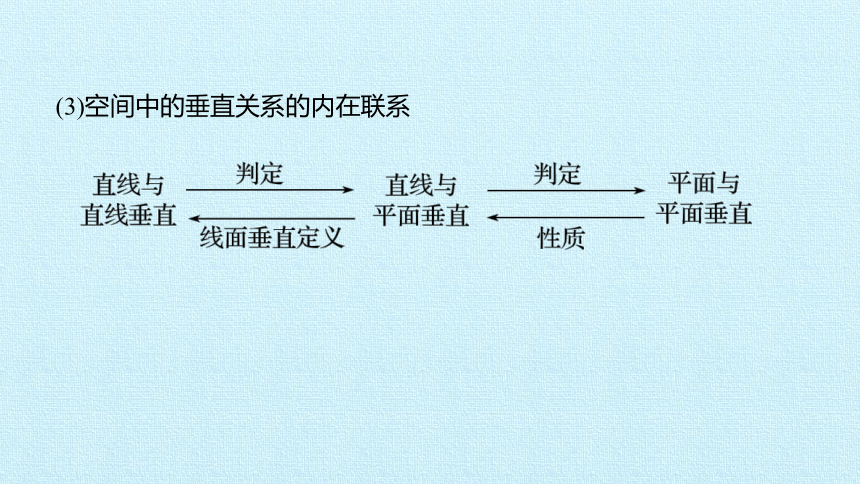
(3)空间中的垂直关系的内在联系
1.设m,n是两条不同的直线,α,β是两个不同的平面,若m∥α,n∥β,α∥β,则m∥n.(
)
2.已知a,b是两异面直线,a⊥b,点P a且P b,一定存在平面α,使P∈α,a∥α且b∥α.(
)
3.平面α∥平面β,直线a∥α,直线b⊥β,那么直线a与直线b的位置关系一定是垂直.(
)
4.球的任意两个大圆的交点的连线是球的直径.(
)
5.若m,n在平面α内的射影依次是一个点和一条直线,且m⊥n,则n α或n∥α.(
)
[思考辨析
判断正误]
√
×
√
√
√
题型探究
类型一 平行问题
例1 如图所示,四边形ABCD是平行四边形,PB⊥平面ABCD,MA∥PB,PB=2MA.在线段PB上是否存在一点F,使平面AFC∥平面PMD?若存在,请确定点F的位置;若不存在,请说明理由.
解答
解 当点F是PB的中点时,平面AFC∥平面PMD,
证明如下:如图连接AC和BD交于点O,连接FO,
∵四边形ABCD是平行四边形,
∴O是BD的中点.∴OF∥PD.
又OF 平面PMD,PD 平面PMD,
∴PF∥MA,PF=MA.
∴四边形AFPM是平行四边形.
∴AF∥PM.
又AF 平面PMD,PM 平面PMD.
∴AF∥平面PMD.
又AF∩OF=F,AF 平面AFC,OF 平面AFC.
∴平面AFC∥平面PMD.
反思与感悟 (1)证明线线平行的依据
①平面几何法(常用的有三角形中位线、平行四边形对边平行);②公理4;③线面平行的性质定理;④面面平行的性质定理;⑤线面垂直的性质定理.
(2)证明线面平行的依据
①定义;②线面平行的判定定理;③面面平行的性质.
(3)证明面面平行的依据
①定义;②面面平行的判定定理;③线面垂直的性质;④面面平行的传递性.
跟踪训练1 如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
(1)证明:GH∥EF;
证明
证明 因为BC∥平面GEFH,BC 平面PBC,
且平面PBC∩平面GEFH=GH,
所以GH∥BC.
同理可证EF∥BC,
因此GH∥EF.
(2)若EB=2,求四边形GEFH的面积.
解答
解 连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,
同理可得PO⊥BD.
又BD∩AC=O,且AC,BD 平面ABCD,
所以PO⊥平面ABCD.
又因为平面GEFH⊥平面ABCD,
所以平面GEFH必过平面ABCD的一条垂线,
所以PO平行于这条垂线,
且PO 平面GEFH,所以PO∥平面GEFH.
又因为平面PBD∩平面GEFH=GK,PO 平面PBD,
所以PO∥GK,
所以GK⊥平面ABCD.
又EF 平面ABCD,
所以GK⊥EF,所以GK是梯形GEFH的高.
由AB=8,EB=2,得EB∶AB=KB∶DB=1∶4,
所以GK=3,
类型二 垂直问题
例2 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
证明:(1)CD⊥AE;
证明 在四棱锥P-ABCD中,
∵PA⊥底面ABCD,CD 平面ABCD,
∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,PA,AC 平面PAC,
∴CD⊥平面PAC.
而AE 平面PAC,∴CD⊥AE.
证明
(2)PD⊥平面ABE.
证明
证明 由PA=AB=BC,∠ABC=60°,可得AC=PA.
∵E是PC的中点,
∴AE⊥PC.
由(1)知,AE⊥CD,
且PC∩CD=C,PC,CD 平面PCD,
∴AE⊥平面PCD.
而PD 平面PCD,
∴AE⊥PD.
∵PA⊥底面ABCD,AB 底面ABCD,
∴PA⊥AB.
又∵AB⊥AD且PA∩AD=A,PA,AD 平面PAD,
∴AB⊥平面PAD,而PD 平面PAD,
∴AB⊥PD.
又∵AB∩AE=A,AB,AE 平面ABE,
∴PD⊥平面ABE.
反思与感悟 (1)两条异面直线相互垂直的证明方法
①定义;
②线面垂直的性质.
(2)直线和平面垂直的证明方法
①线面垂直的判定定理;
②面面垂直的性质定理.
(3)平面和平面相互垂直的证明方法
①定义;
②面面垂直的判定定理.
证明
跟踪训练2 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面ABC上的射影恰好是BC的中点,且BC=CA=AA1.
(1)求证:平面ACC1A1⊥平面B1C1CB;
证明 设BC的中点为M,
∵点B1在底面ABC上的射影恰好是点M,
∴B1M⊥平面ABC.
∵AC 平面ABC,
∴B1M⊥AC.
又∵BC⊥AC,B1M∩BC=M,B1M,BC 平面B1C1CB,
∴AC⊥平面B1C1CB.
又∵AC 平面ACC1A1,
∴平面ACC1A1⊥平面B1C1CB.
证明
(2)求证:BC1⊥AB1.
证明 连接B1C.
∵AC⊥平面B1C1CB,
∴AC⊥BC1.
在斜三棱柱ABC-A1B1C1中,
∵BC=CC1.
∴四边形B1C1CB是菱形,
∴B1C⊥BC1.
又∵B1C∩AC=C,
∴BC1⊥平面ACB1,
∴BC1⊥AB1.
达标检测
解析 ②如果m γ,则m不平行于γ;
③若m∥α,n∥α,则m,n相交,平行或异面,
④若α⊥γ,β⊥γ,则α,β相交或平行.
解析
答案
1.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个说法:
①若m⊥α,n∥α,则m⊥n;②若α∥β,β∥γ,m∥α,则m∥γ;③若m∥α,n∥α,则m∥n;④若α⊥γ,β⊥γ,则α∥β.
其中正确说法的序号是
A.①
B.②③
C.③④
D.①④
√
证明
2.如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.
(1)求证:VB∥平面MOC;
证明 因为O,M分别为AB,VA的中点,
所以OM∥VB.
又因为VB 平面MOC,OM 平面MOC,
所以VB∥平面MOC.
证明
(2)求证:平面MOC⊥平面VAB.
证明 因为AC=BC,O为AB的中点,
所以OC⊥AB.
又因为平面VAB⊥平面ABC,
平面VAB∩平面ABC=AB,
且OC 平面ABC,
所以OC⊥平面VAB.
又因为OC 平面MOC,
所以平面MOC⊥平面VAB.
谢
谢
第14章
空间直线与平面
复习课件
知识梳理
达标检测
题型探究
内容索引
知识梳理
1.四个公理
公理1:如果一条直线上的
在一个平面内,那么这条直线上所有的点都在这个平面内.
公理2:过
的三点,有且只有一个平面.
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有
.
公理4:平行于同一条直线的两条直线互相
.
两点
不在同一条直线上
一条过该点的公共直线
平行
2.直线与直线的位置关系
_____
共面直线
______
异面直线:不同在______一个平面内,没有公共点
平行
任何
相交
判定
性质
定义
定理
图形
条件
________
___________
______
_______
____________
________
结论
a∥α
b∥α
a∩α=
a∥b
3.平行的判定与性质
(1)直线与平面平行的判定与性质
a∩α=
a α,b α,
a∥b
a∥α,a β,
α∩β=b
a∥α
(2)面面平行的判定与性质
α∩β=
判定
性质
定义
定理
图形
条件
_________
___________
___________
___________
___________
___________
________
α∥β,a β
结论
α∥β
α∥β
a∥b
a∥α
a β,b β,
a∩b=P,
a∥α,b∥α
α∥β,
α∩γ=a,
β∩γ=b
(3)空间中的平行关系的内在联系
4.垂直的判定与性质
(1)直线与平面垂直
任意
图形
条件
结论
判定
a⊥b,b α
(b为α内的
直线)
a⊥α
a⊥m,a⊥n,m,n α,
___________
a⊥α
a∥b,______
b⊥α
m∩n=O
a⊥α
性质
a⊥α,______
a⊥b
a⊥α,b⊥α
______
b α
a∥b
(2)平面与平面垂直的判定与性质定理
文字语言
图形语言
符号语言
判定
定理
如果一个平面经过另一个平面的一条
,那么这两个平面互相垂直
α⊥β
性质
定理
如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面
l⊥α
垂线
(3)空间中的垂直关系的内在联系
1.设m,n是两条不同的直线,α,β是两个不同的平面,若m∥α,n∥β,α∥β,则m∥n.(
)
2.已知a,b是两异面直线,a⊥b,点P a且P b,一定存在平面α,使P∈α,a∥α且b∥α.(
)
3.平面α∥平面β,直线a∥α,直线b⊥β,那么直线a与直线b的位置关系一定是垂直.(
)
4.球的任意两个大圆的交点的连线是球的直径.(
)
5.若m,n在平面α内的射影依次是一个点和一条直线,且m⊥n,则n α或n∥α.(
)
[思考辨析
判断正误]
√
×
√
√
√
题型探究
类型一 平行问题
例1 如图所示,四边形ABCD是平行四边形,PB⊥平面ABCD,MA∥PB,PB=2MA.在线段PB上是否存在一点F,使平面AFC∥平面PMD?若存在,请确定点F的位置;若不存在,请说明理由.
解答
解 当点F是PB的中点时,平面AFC∥平面PMD,
证明如下:如图连接AC和BD交于点O,连接FO,
∵四边形ABCD是平行四边形,
∴O是BD的中点.∴OF∥PD.
又OF 平面PMD,PD 平面PMD,
∴PF∥MA,PF=MA.
∴四边形AFPM是平行四边形.
∴AF∥PM.
又AF 平面PMD,PM 平面PMD.
∴AF∥平面PMD.
又AF∩OF=F,AF 平面AFC,OF 平面AFC.
∴平面AFC∥平面PMD.
反思与感悟 (1)证明线线平行的依据
①平面几何法(常用的有三角形中位线、平行四边形对边平行);②公理4;③线面平行的性质定理;④面面平行的性质定理;⑤线面垂直的性质定理.
(2)证明线面平行的依据
①定义;②线面平行的判定定理;③面面平行的性质.
(3)证明面面平行的依据
①定义;②面面平行的判定定理;③线面垂直的性质;④面面平行的传递性.
跟踪训练1 如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
(1)证明:GH∥EF;
证明
证明 因为BC∥平面GEFH,BC 平面PBC,
且平面PBC∩平面GEFH=GH,
所以GH∥BC.
同理可证EF∥BC,
因此GH∥EF.
(2)若EB=2,求四边形GEFH的面积.
解答
解 连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,
同理可得PO⊥BD.
又BD∩AC=O,且AC,BD 平面ABCD,
所以PO⊥平面ABCD.
又因为平面GEFH⊥平面ABCD,
所以平面GEFH必过平面ABCD的一条垂线,
所以PO平行于这条垂线,
且PO 平面GEFH,所以PO∥平面GEFH.
又因为平面PBD∩平面GEFH=GK,PO 平面PBD,
所以PO∥GK,
所以GK⊥平面ABCD.
又EF 平面ABCD,
所以GK⊥EF,所以GK是梯形GEFH的高.
由AB=8,EB=2,得EB∶AB=KB∶DB=1∶4,
所以GK=3,
类型二 垂直问题
例2 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
证明:(1)CD⊥AE;
证明 在四棱锥P-ABCD中,
∵PA⊥底面ABCD,CD 平面ABCD,
∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,PA,AC 平面PAC,
∴CD⊥平面PAC.
而AE 平面PAC,∴CD⊥AE.
证明
(2)PD⊥平面ABE.
证明
证明 由PA=AB=BC,∠ABC=60°,可得AC=PA.
∵E是PC的中点,
∴AE⊥PC.
由(1)知,AE⊥CD,
且PC∩CD=C,PC,CD 平面PCD,
∴AE⊥平面PCD.
而PD 平面PCD,
∴AE⊥PD.
∵PA⊥底面ABCD,AB 底面ABCD,
∴PA⊥AB.
又∵AB⊥AD且PA∩AD=A,PA,AD 平面PAD,
∴AB⊥平面PAD,而PD 平面PAD,
∴AB⊥PD.
又∵AB∩AE=A,AB,AE 平面ABE,
∴PD⊥平面ABE.
反思与感悟 (1)两条异面直线相互垂直的证明方法
①定义;
②线面垂直的性质.
(2)直线和平面垂直的证明方法
①线面垂直的判定定理;
②面面垂直的性质定理.
(3)平面和平面相互垂直的证明方法
①定义;
②面面垂直的判定定理.
证明
跟踪训练2 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面ABC上的射影恰好是BC的中点,且BC=CA=AA1.
(1)求证:平面ACC1A1⊥平面B1C1CB;
证明 设BC的中点为M,
∵点B1在底面ABC上的射影恰好是点M,
∴B1M⊥平面ABC.
∵AC 平面ABC,
∴B1M⊥AC.
又∵BC⊥AC,B1M∩BC=M,B1M,BC 平面B1C1CB,
∴AC⊥平面B1C1CB.
又∵AC 平面ACC1A1,
∴平面ACC1A1⊥平面B1C1CB.
证明
(2)求证:BC1⊥AB1.
证明 连接B1C.
∵AC⊥平面B1C1CB,
∴AC⊥BC1.
在斜三棱柱ABC-A1B1C1中,
∵BC=CC1.
∴四边形B1C1CB是菱形,
∴B1C⊥BC1.
又∵B1C∩AC=C,
∴BC1⊥平面ACB1,
∴BC1⊥AB1.
达标检测
解析 ②如果m γ,则m不平行于γ;
③若m∥α,n∥α,则m,n相交,平行或异面,
④若α⊥γ,β⊥γ,则α,β相交或平行.
解析
答案
1.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个说法:
①若m⊥α,n∥α,则m⊥n;②若α∥β,β∥γ,m∥α,则m∥γ;③若m∥α,n∥α,则m∥n;④若α⊥γ,β⊥γ,则α∥β.
其中正确说法的序号是
A.①
B.②③
C.③④
D.①④
√
证明
2.如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.
(1)求证:VB∥平面MOC;
证明 因为O,M分别为AB,VA的中点,
所以OM∥VB.
又因为VB 平面MOC,OM 平面MOC,
所以VB∥平面MOC.
证明
(2)求证:平面MOC⊥平面VAB.
证明 因为AC=BC,O为AB的中点,
所以OC⊥AB.
又因为平面VAB⊥平面ABC,
平面VAB∩平面ABC=AB,
且OC 平面ABC,
所以OC⊥平面VAB.
又因为OC 平面MOC,
所以平面MOC⊥平面VAB.
谢
谢
