沪教版(上海)数学高三下册-18.1 总体和样本 (课件)(共30张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三下册-18.1 总体和样本 (课件)(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
总体和样本
随着社会的发展,一个城市的人口构成发生
变化,为了了解整个城市乃至全国的人口
情况,国家会每隔一段时间进行一次人口普查,
并从中发现问题,制定对策。
一个人生病后去医院看病,很可能就要验血,医生从病人手指上采一滴血,就能查出病人的病因所在。
环境监测人员从河水中取一瓶水,就能查出河水是否受到污染或受污染的严重程度。
如何从调查所获得的数据中得出有用的信息,
是数学的一个分支——统计学研究的范畴。
1、总体与个体
在统计问题中,我们把研究对象的全体
叫做总体,总体中的每一个对象叫做个体。
从总体所含个体的数量上看,总体可分为
有限总体和无限总体两类。
高中阶段只讨论有限总体的问题
如果总体有N个个体,他们的值分别为
那么
叫做总体均值。
总体均值表示总体中所有个体的
平均大小,即一般水平。
总体均值在很多方面有着广泛的应用。
2、总体均值
例如:
在讨论上海的家庭户规模时,我们
要考察家庭户的人口数。根据2000年
第五次人口普查资料,上海共有529.91万
户,1478.2万人口,那么每个家庭户的人口数总体均值是多少?
我要工作!
案例:
只有3.5万?!
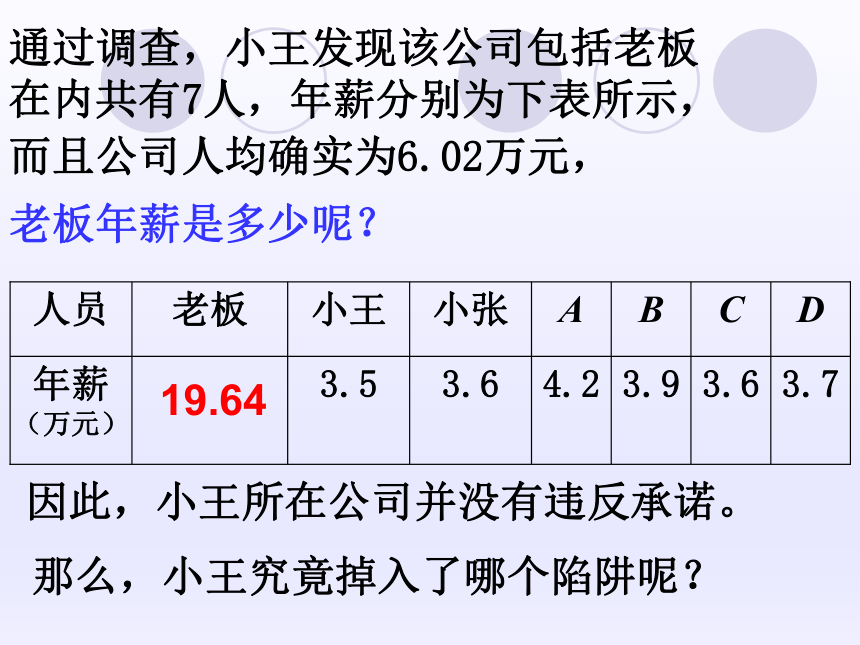
通过调查,小王发现该公司包括老板
在内共有7人,年薪分别为下表所示,
3.7
3.6
3.9
4.2
3.6
3.5
年薪
(万元)
D
C
B
A
小张
小王
老板
人员
19.64
因此,小王所在公司并没有违反承诺。
那么,小王究竟掉入了哪个陷阱呢?
而且公司人均确实为6.02万元,
老板年薪是多少呢?
依由小到大的顺序排列,当N为奇数时,位于该数列正中位置的数叫做总体的中位数,记作m。当N为偶数时,位于该数列正中位置的两个数的平均数叫做总体的中位数。
把总体中的各个个体
中位数把总体分成个数相等的两个部分,其中一部分的值都大于或等于中位数,另一部分的值小于或等于中位数。
3、总体的中位数
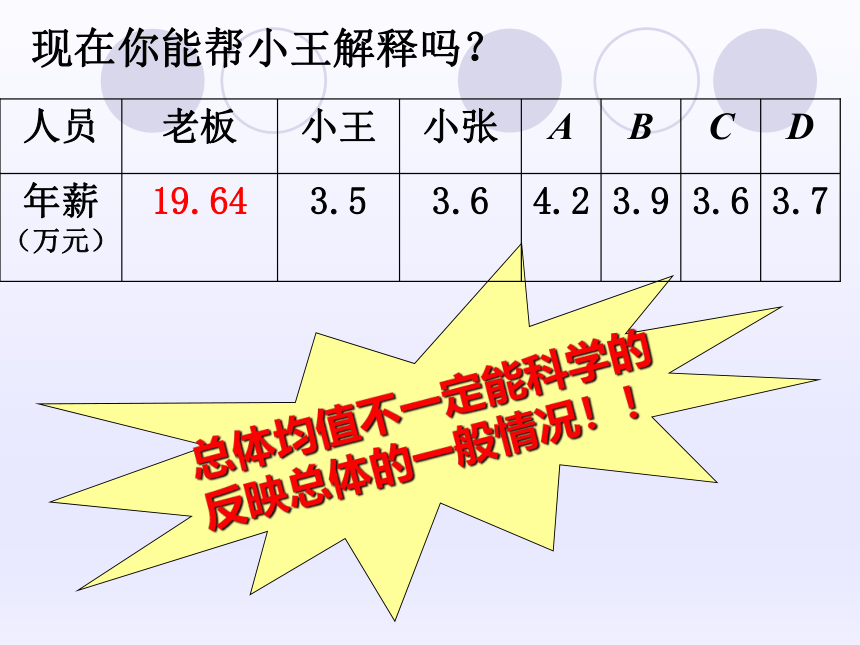
现在你能帮小王解释吗?
总体均值不一定能科学的
反映总体的一般情况!!
3.7
3.6
3.9
4.2
3.6
3.5
19.64
年薪
(万元)
D
C
B
A
小张
小王
老板
人员
杨家有财一千万,
富豪村
九个邻居穷光蛋,
取个平均算一算,
家家都是杨百万。
你认为这个村名副其实吗?
为什么呢?
从这个案例中,我们可以看到总体均值
和总体中位数虽然都反映了总体中各个
个体的“平均”水平。
但实质却不同:
总体均值反映总体中各个个体的平均大小,
总体中位数反映总体的中间值(中等水平)。
之后,小王和小张再次来到招聘会现场。
招聘启事
本公司招聘新工……
平均年薪6万元,
中位数6万元,……
印度洋有限公司
经查,小王所在公司共有10人,
小张所在公司共有8人,
一年后,小王得到的年薪是3.6万元。
小张得到的年薪是5.2万元。
年薪分别为:
人员
老板
小王
A
B
C
年薪
(万元)
13.6
3.6
4.1
2.3
9.2
人员
D
E
F
G
H
年薪
(万元)
10.2
2.5
6.4
7.1
6.7
人员
老板
小张
I
J
年薪
(万元)
9.1
5.2
5.1
6.1
人员
K
L
M
N
年薪
(万元)
6.7
6.3
7.3
5.4
请计算他们的总体均值和中位数。
4、总体方差
设总体有N个个体,分别为
各个个体与总体均值的差的平方分别是
我们把它们的平均数叫做总体方差,
记作
总体方差反映了个体之间的差异,
即数据偏离平均数的程度。
方差越大,总体中各个个体之间的
差别越大;
方差越小,总体中各个个体之间的差别越小。
总体方差也可表示为:
5、总体标准差
总体方差的算术平方根叫做总体标准差,
即:
人员
老板
小王
A
B
C
年薪
(万元)
13.6
3.6
4.1
2.3
9.2
人员
D
E
F
G
H
年薪
(万元)
10.2
2.5
6.4
7.1
6.7
人员
老板
小张
I
J
年薪
(万元)
9.1
5.2
5.1
6.1
人员
K
L
M
N
年薪
(万元)
6.7
6.3
7.3
5.4
请计算他们的总体方差。
甲、乙两个公司各有五人,其中
甲公司五人的年薪分别为5,9,8,10,8;乙公司五人的年薪为6,10,3,12,9;
问:
(1)哪家公司的平均年薪高些?
(2)哪家公司内部的年薪差别小些?
要是你会选择哪家公司呢?
思考1:
已知某公司10名职工的年薪由小到大
依次为3,5,5,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5。
若要使他们之间工资差别最小,则a、b的值分别是
。
思考2:
某公司的每位员工工资都加上80元
构成一组新数据,则这组新数据的
方差是4.4,那么原来他们工资的方差为
。
你能从总体方差的含义上解释这个结果吗?
思考3:
练习:
(1)在一个班级50名学生中,30名男生的平均身高是1.60米,20名女生的平均身高是1.50米,那么这个班学生的平均身高是________米.
(2)若2,7,6和
x
四个数的平均数是5;18,1,6,15,x
与
y
六个数的中位数是10,则
y
=_______.
(3)已知在n个数据中,x1出现
f1
次,x2出现
f2,…,xk出现
fk次
(f1+f2+f3+…+fk=n),x
是这
n
个数据的平均数,求:
f1(x1–x)
+
f2(x2–x)
+…+
fk(xk–x)
(4)从同一家工厂生产的20瓦日光灯中抽出6支,40瓦日光灯中抽出8支进行使用寿命(单位:小时)测试,结果如下:
20瓦
457
443
459
451
464
438
40瓦
466
452
438
467
455
459
464
439
哪种日光灯的寿命长?哪种日光灯的质量比较稳定?
(5)设等差数列
的公差为
,若
的方差为1,则
=________.
(6)已知
x
是1,2,3,x,5,6,7这七个数的中位数,且1,3,x2,-y
这四个
数的平均数为1,那么
的最小值为__________
(7)已知点A1(x1
,y1),A2(x2
,y2),…,
An(xn
,yn)均在直线
y
=
2x-3
上,若x1
,x2
,…,
xn
的标准差和平均数分别为
2
和
3
,则
y1
,
y2
,…,
yn
的标准差和平均数分别为___________
(8)在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
(A)甲地:总体均值为3,中位数为4
(B)乙地:总体均值为1,总体方差大于0
(C)丙地:中位数为2,众数为3
(D)丁地:总体均值为2,总体方差为3
总体和样本
随着社会的发展,一个城市的人口构成发生
变化,为了了解整个城市乃至全国的人口
情况,国家会每隔一段时间进行一次人口普查,
并从中发现问题,制定对策。
一个人生病后去医院看病,很可能就要验血,医生从病人手指上采一滴血,就能查出病人的病因所在。
环境监测人员从河水中取一瓶水,就能查出河水是否受到污染或受污染的严重程度。
如何从调查所获得的数据中得出有用的信息,
是数学的一个分支——统计学研究的范畴。
1、总体与个体
在统计问题中,我们把研究对象的全体
叫做总体,总体中的每一个对象叫做个体。
从总体所含个体的数量上看,总体可分为
有限总体和无限总体两类。
高中阶段只讨论有限总体的问题
如果总体有N个个体,他们的值分别为
那么
叫做总体均值。
总体均值表示总体中所有个体的
平均大小,即一般水平。
总体均值在很多方面有着广泛的应用。
2、总体均值
例如:
在讨论上海的家庭户规模时,我们
要考察家庭户的人口数。根据2000年
第五次人口普查资料,上海共有529.91万
户,1478.2万人口,那么每个家庭户的人口数总体均值是多少?
我要工作!
案例:
只有3.5万?!
通过调查,小王发现该公司包括老板
在内共有7人,年薪分别为下表所示,
3.7
3.6
3.9
4.2
3.6
3.5
年薪
(万元)
D
C
B
A
小张
小王
老板
人员
19.64
因此,小王所在公司并没有违反承诺。
那么,小王究竟掉入了哪个陷阱呢?
而且公司人均确实为6.02万元,
老板年薪是多少呢?
依由小到大的顺序排列,当N为奇数时,位于该数列正中位置的数叫做总体的中位数,记作m。当N为偶数时,位于该数列正中位置的两个数的平均数叫做总体的中位数。
把总体中的各个个体
中位数把总体分成个数相等的两个部分,其中一部分的值都大于或等于中位数,另一部分的值小于或等于中位数。
3、总体的中位数
现在你能帮小王解释吗?
总体均值不一定能科学的
反映总体的一般情况!!
3.7
3.6
3.9
4.2
3.6
3.5
19.64
年薪
(万元)
D
C
B
A
小张
小王
老板
人员
杨家有财一千万,
富豪村
九个邻居穷光蛋,
取个平均算一算,
家家都是杨百万。
你认为这个村名副其实吗?
为什么呢?
从这个案例中,我们可以看到总体均值
和总体中位数虽然都反映了总体中各个
个体的“平均”水平。
但实质却不同:
总体均值反映总体中各个个体的平均大小,
总体中位数反映总体的中间值(中等水平)。
之后,小王和小张再次来到招聘会现场。
招聘启事
本公司招聘新工……
平均年薪6万元,
中位数6万元,……
印度洋有限公司
经查,小王所在公司共有10人,
小张所在公司共有8人,
一年后,小王得到的年薪是3.6万元。
小张得到的年薪是5.2万元。
年薪分别为:
人员
老板
小王
A
B
C
年薪
(万元)
13.6
3.6
4.1
2.3
9.2
人员
D
E
F
G
H
年薪
(万元)
10.2
2.5
6.4
7.1
6.7
人员
老板
小张
I
J
年薪
(万元)
9.1
5.2
5.1
6.1
人员
K
L
M
N
年薪
(万元)
6.7
6.3
7.3
5.4
请计算他们的总体均值和中位数。
4、总体方差
设总体有N个个体,分别为
各个个体与总体均值的差的平方分别是
我们把它们的平均数叫做总体方差,
记作
总体方差反映了个体之间的差异,
即数据偏离平均数的程度。
方差越大,总体中各个个体之间的
差别越大;
方差越小,总体中各个个体之间的差别越小。
总体方差也可表示为:
5、总体标准差
总体方差的算术平方根叫做总体标准差,
即:
人员
老板
小王
A
B
C
年薪
(万元)
13.6
3.6
4.1
2.3
9.2
人员
D
E
F
G
H
年薪
(万元)
10.2
2.5
6.4
7.1
6.7
人员
老板
小张
I
J
年薪
(万元)
9.1
5.2
5.1
6.1
人员
K
L
M
N
年薪
(万元)
6.7
6.3
7.3
5.4
请计算他们的总体方差。
甲、乙两个公司各有五人,其中
甲公司五人的年薪分别为5,9,8,10,8;乙公司五人的年薪为6,10,3,12,9;
问:
(1)哪家公司的平均年薪高些?
(2)哪家公司内部的年薪差别小些?
要是你会选择哪家公司呢?
思考1:
已知某公司10名职工的年薪由小到大
依次为3,5,5,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5。
若要使他们之间工资差别最小,则a、b的值分别是
。
思考2:
某公司的每位员工工资都加上80元
构成一组新数据,则这组新数据的
方差是4.4,那么原来他们工资的方差为
。
你能从总体方差的含义上解释这个结果吗?
思考3:
练习:
(1)在一个班级50名学生中,30名男生的平均身高是1.60米,20名女生的平均身高是1.50米,那么这个班学生的平均身高是________米.
(2)若2,7,6和
x
四个数的平均数是5;18,1,6,15,x
与
y
六个数的中位数是10,则
y
=_______.
(3)已知在n个数据中,x1出现
f1
次,x2出现
f2,…,xk出现
fk次
(f1+f2+f3+…+fk=n),x
是这
n
个数据的平均数,求:
f1(x1–x)
+
f2(x2–x)
+…+
fk(xk–x)
(4)从同一家工厂生产的20瓦日光灯中抽出6支,40瓦日光灯中抽出8支进行使用寿命(单位:小时)测试,结果如下:
20瓦
457
443
459
451
464
438
40瓦
466
452
438
467
455
459
464
439
哪种日光灯的寿命长?哪种日光灯的质量比较稳定?
(5)设等差数列
的公差为
,若
的方差为1,则
=________.
(6)已知
x
是1,2,3,x,5,6,7这七个数的中位数,且1,3,x2,-y
这四个
数的平均数为1,那么
的最小值为__________
(7)已知点A1(x1
,y1),A2(x2
,y2),…,
An(xn
,yn)均在直线
y
=
2x-3
上,若x1
,x2
,…,
xn
的标准差和平均数分别为
2
和
3
,则
y1
,
y2
,…,
yn
的标准差和平均数分别为___________
(8)在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
(A)甲地:总体均值为3,中位数为4
(B)乙地:总体均值为1,总体方差大于0
(C)丙地:中位数为2,众数为3
(D)丁地:总体均值为2,总体方差为3
