沪教版(上海)数学高三上册-16.5 二项式定理 课件8(共24张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.5 二项式定理 课件8(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:41:59 | ||
图片预览







文档简介
(共24张PPT)
二
项
式
定
理
复习提问
1.二项式定理的内容
(a+b)n=
Cnan+Cnan-1b+…+Cnan-kbk+…+Cnbn
0
1
k
n
右边多项式叫(a+b)n的二项展开式;
2.二项式系数:
3.二项展开式的通项Tk+1=
针对(a+b)n的
标准形式而言
(b+a)n,(a-b)n的通项则分别为:
4.在定理中,令a=1,b=x,则
二项式定理的逆用
例1
计算并求值
解(1):将原式变形
例1
计算并求值
解:(2)原式
逆向应用公式和变形应用公式是高中数学的难点,也是重点,只有熟练掌握公式的正用,才能掌握逆向应用和变式应用
观察猜想
展开式的二项式系数有什么变化规律?
二项式系数最大的是哪一项?
(a+b)n=
Cnan+Cnan-1b+…+Cnan-rbr+…+Cnbn
0
1
r
n
研究它的一般规律,我们先来观察
n为特殊值时,二项展开式中二项式系
数有什么特点?
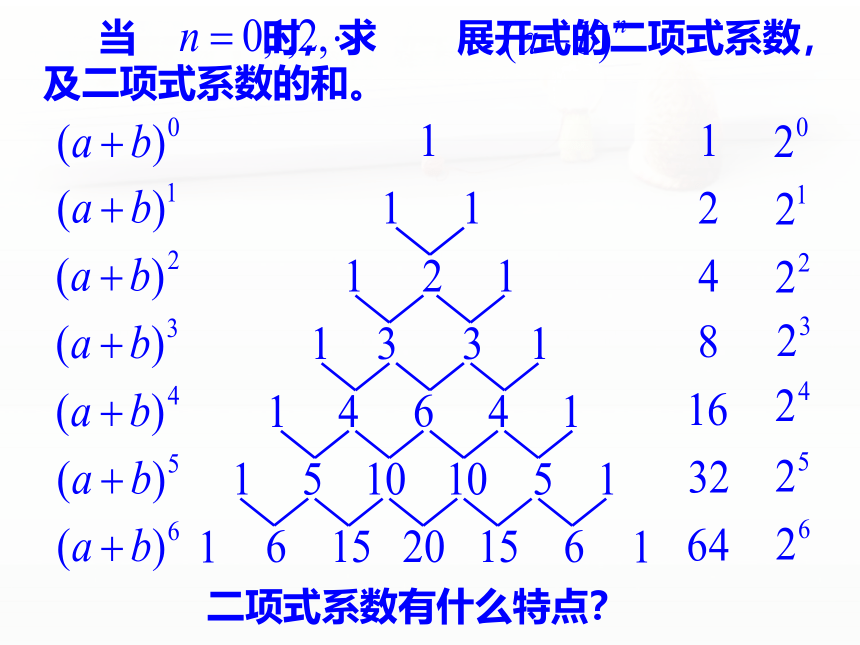
当
时,求
展开式的二项式系数,及二项式系数的和。
二项式系数有什么特点?
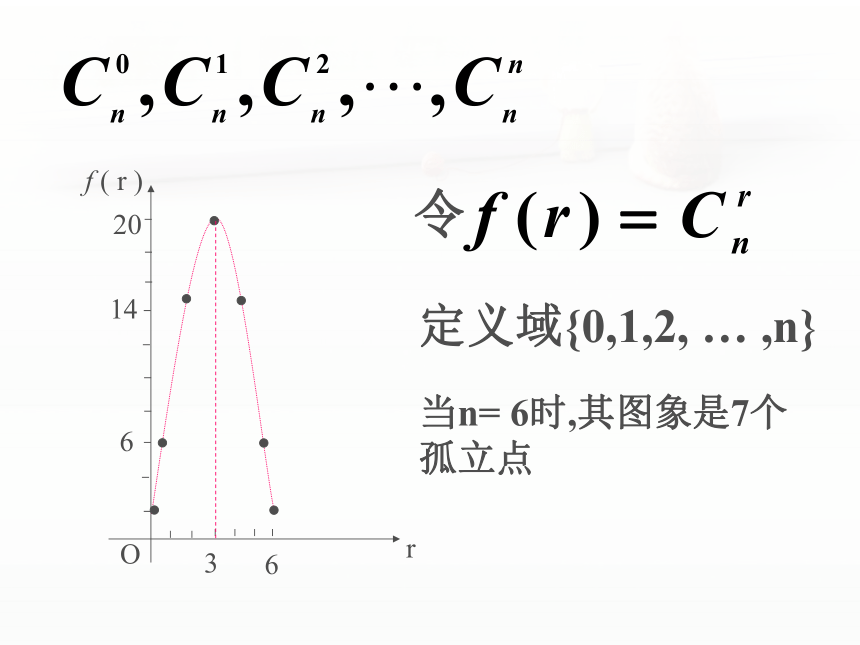
定义域{0,1,2,
…
,n}
6
14
20
O
6
3
r
f
(
r
)
令
当n=
6时,其图象是7个孤立点
归纳提高
性质1 (对称性):
在二项展开式中,与首末两端“等距”的
两项的二项式系数相等。即
一般地,
展开式的二项式系数
有如下性质:
注:在杨辉三角表里,每一个数都等于它肩上两个数的和
归纳提高
性质2(增减性与最大值):
若n为偶数
中间一项(第
项)的二项式系数取得
最大值;即最
大
。
当r≤
时,
单调递增;
当r≥
时,
单调递减;
归纳提高
性质2(增减性与最大值):
中间两项(第
、
项)的二项式系数相等,且同时取得最大值。即
若n为奇数
当r≤
时,
单调递增;
当r≥
时,
单调递减;
例题分析
例2
证明:
(1)(a
+
b)n
的展开式中,各二项式系数
的和为2n;
(2)
(a
+
b)n的展开式中,奇数项的二
项式系数的和等于偶数项的二项式
系数的和。
小结:求解二项式系数和时,灵活运用赋值
法可以使问题简单化。通常选取赋值
时取-1,1。
性质3(各二项式系数的和)
:
性质4(奇数项的二项式系数和等于偶数项
的二项式系数和):
归纳提高
求奇数(次)项偶数(次)项系数的和
(1)
(2)
求奇数(次)项偶数(次)项系数的和
所以
(3)
例题点评
求二项展开式系数和,常常得用赋值法,设
二项式中的字母为1或-1,得到一个或几个等
式,再根据结果求值
求多项式的展开式中特定的项(系数)
例4
的展开式中,
的系数等于___________
解:仔细观察所给已知条件可直接求得
的系
数是
解法2
运用等比数列求和公式得
在
的展开式中,含有
项的系数为
所以
的系数为-20
求复杂的代数式的展开式中某项(某项的系数),可以逐项分析求解,常常对所给代数式进行化简,可以减小计算量
例题点评
例5
求
的展开式中
项
的系数.
解
的通项是
的通项是
的通项是
由题意知
解得
所以
的系数为:
例题点评
对于较为复杂的二项式与二项式乘积利用两
个通项之积比较方便运算
求展开式中系数最大(小)的项
解:
设
项是系数最大的项,则
二项式系数最大的项为第11项,即
所以它们的比是
例
7
在
的展开式中,系数绝对值最大的项
解:设系数绝对值最大的项是第r+1项,则
所以当
时,系数绝对值最大的项为
解决系数最大问题,通常设第
项是系数最
大的项,则有
由此确定r的取值
例题点评
三项式转化为二项式
解:三项式不能用二项式定理,必须转化为二项式
再利用二项式定理逐项分析常数项得
=1107
___________
解:
原式化为
其通项公式为
240
例题点评
括号里含有三项的情况可以把某两项合并为一项,合并时要注意选择的科学性.也可因式分解化为乘积二项式.
二
项
式
定
理
复习提问
1.二项式定理的内容
(a+b)n=
Cnan+Cnan-1b+…+Cnan-kbk+…+Cnbn
0
1
k
n
右边多项式叫(a+b)n的二项展开式;
2.二项式系数:
3.二项展开式的通项Tk+1=
针对(a+b)n的
标准形式而言
(b+a)n,(a-b)n的通项则分别为:
4.在定理中,令a=1,b=x,则
二项式定理的逆用
例1
计算并求值
解(1):将原式变形
例1
计算并求值
解:(2)原式
逆向应用公式和变形应用公式是高中数学的难点,也是重点,只有熟练掌握公式的正用,才能掌握逆向应用和变式应用
观察猜想
展开式的二项式系数有什么变化规律?
二项式系数最大的是哪一项?
(a+b)n=
Cnan+Cnan-1b+…+Cnan-rbr+…+Cnbn
0
1
r
n
研究它的一般规律,我们先来观察
n为特殊值时,二项展开式中二项式系
数有什么特点?
当
时,求
展开式的二项式系数,及二项式系数的和。
二项式系数有什么特点?
定义域{0,1,2,
…
,n}
6
14
20
O
6
3
r
f
(
r
)
令
当n=
6时,其图象是7个孤立点
归纳提高
性质1 (对称性):
在二项展开式中,与首末两端“等距”的
两项的二项式系数相等。即
一般地,
展开式的二项式系数
有如下性质:
注:在杨辉三角表里,每一个数都等于它肩上两个数的和
归纳提高
性质2(增减性与最大值):
若n为偶数
中间一项(第
项)的二项式系数取得
最大值;即最
大
。
当r≤
时,
单调递增;
当r≥
时,
单调递减;
归纳提高
性质2(增减性与最大值):
中间两项(第
、
项)的二项式系数相等,且同时取得最大值。即
若n为奇数
当r≤
时,
单调递增;
当r≥
时,
单调递减;
例题分析
例2
证明:
(1)(a
+
b)n
的展开式中,各二项式系数
的和为2n;
(2)
(a
+
b)n的展开式中,奇数项的二
项式系数的和等于偶数项的二项式
系数的和。
小结:求解二项式系数和时,灵活运用赋值
法可以使问题简单化。通常选取赋值
时取-1,1。
性质3(各二项式系数的和)
:
性质4(奇数项的二项式系数和等于偶数项
的二项式系数和):
归纳提高
求奇数(次)项偶数(次)项系数的和
(1)
(2)
求奇数(次)项偶数(次)项系数的和
所以
(3)
例题点评
求二项展开式系数和,常常得用赋值法,设
二项式中的字母为1或-1,得到一个或几个等
式,再根据结果求值
求多项式的展开式中特定的项(系数)
例4
的展开式中,
的系数等于___________
解:仔细观察所给已知条件可直接求得
的系
数是
解法2
运用等比数列求和公式得
在
的展开式中,含有
项的系数为
所以
的系数为-20
求复杂的代数式的展开式中某项(某项的系数),可以逐项分析求解,常常对所给代数式进行化简,可以减小计算量
例题点评
例5
求
的展开式中
项
的系数.
解
的通项是
的通项是
的通项是
由题意知
解得
所以
的系数为:
例题点评
对于较为复杂的二项式与二项式乘积利用两
个通项之积比较方便运算
求展开式中系数最大(小)的项
解:
设
项是系数最大的项,则
二项式系数最大的项为第11项,即
所以它们的比是
例
7
在
的展开式中,系数绝对值最大的项
解:设系数绝对值最大的项是第r+1项,则
所以当
时,系数绝对值最大的项为
解决系数最大问题,通常设第
项是系数最
大的项,则有
由此确定r的取值
例题点评
三项式转化为二项式
解:三项式不能用二项式定理,必须转化为二项式
再利用二项式定理逐项分析常数项得
=1107
___________
解:
原式化为
其通项公式为
240
例题点评
括号里含有三项的情况可以把某两项合并为一项,合并时要注意选择的科学性.也可因式分解化为乘积二项式.
