沪教版(上海)数学高三上册-15.5 几何体的体积_(课件)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.5 几何体的体积_(课件) |  | |
| 格式 | ppt | ||
| 文件大小 | 403.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 22:20:02 | ||
图片预览



文档简介
(共10张PPT)
复习引入
一.回顾几种常见的平面多边形的面积公式及一些复杂多边形的面积的计算方法.
二.由长方体(直四棱柱)的体积公式:V
=
S×h
.
对于一般的棱柱其体积的计算方法是怎样的呢
问题的提出:
新课讲解
一.介绍(祖暅原理)的具体内容:
我国古代数学家祖暅在“开立圆术”一书中指出:
(约在公元5世纪)
“夫叠棊(棋)成立积,缘幂势既同,则积不容异”
现代文解释为:
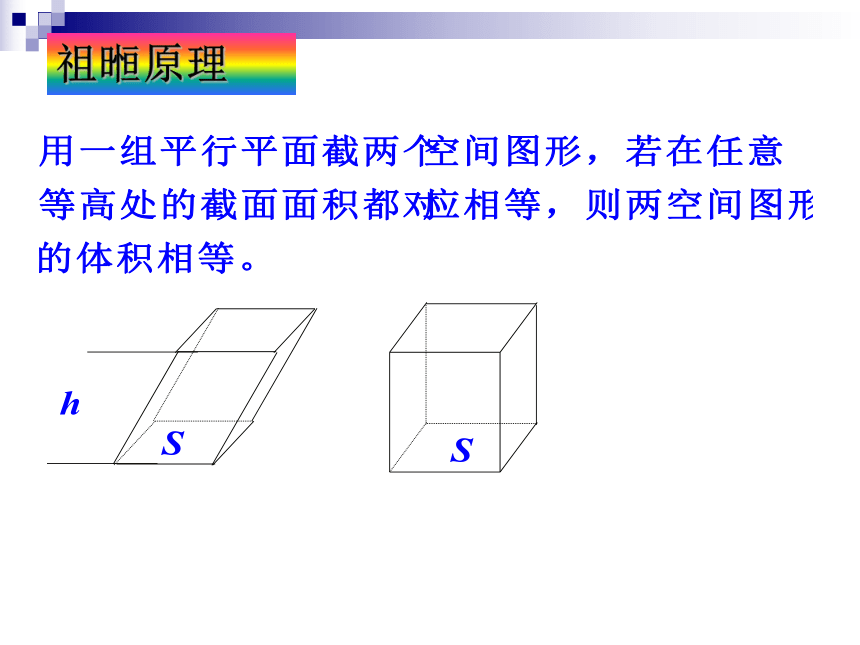
体积可以看成是由面积叠加而成,用一组平行的平面截两个空间图形,若在任意高处的截面面积都对应相等,则两个空间图形的体积必然相等.
说明
①上述论述称为祖暅原理,其正确性可以验证.
②利用叠书法加以理解和感悟.
祖暅原理
S
h
S
S
h
新课讲解
二.棱柱体积公式的推导:
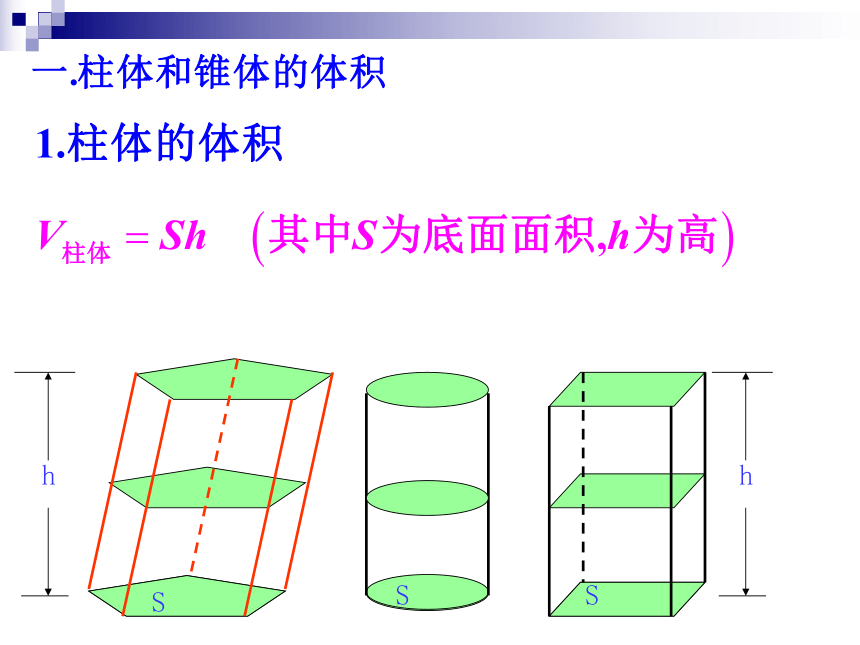
由长方体的体积公式V=S×h.利用祖暅原理,结合推导出:
(棱柱体积公式)--
V棱柱=
S×h
.
新课讲解
例题1
三.棱柱体积的计算.
已知三棱柱
的底面为直角三角形,两直角边AC和BC的长分别为4cm和3cm,侧棱
的长为10cm,求满足下列条件的三棱柱的体积.
(1)侧棱
垂直于底面;
(2)侧棱
与底面所成的角为60°.
例题1
已知三棱柱
的底面为直角三角形,两直角边AC和BC的长分别为4cm和3cm,侧棱
的长为10cm,求满足下列条件的三棱柱的体积.
(1)侧棱
垂直于底面;
(2)侧棱
与底面所成的角为60°.
例题1
已知三棱柱
的底面为直角三角形,两直角边AC和BC的长分别为4cm和3cm,侧棱
的长为10cm,求满足下列条件的三棱柱的体积.
(1)侧棱
垂直于底面;
(2)侧棱
与底面所成的角为60°.
归纳总结
①计算棱柱体积,关键是计算棱柱的底面积和棱柱的高.
②为方便计算棱柱的底面积,可以把棱柱的底面多边形画成其平面图形.
③注意区分棱柱的侧棱与棱柱的高之间的区别.
在直棱柱中:
侧棱=高;
而在一般的斜棱柱中:侧棱与高并不相等,但侧棱与高加上侧棱在底面上的射影构成一个Rt△.
复习引入
一.回顾几种常见的平面多边形的面积公式及一些复杂多边形的面积的计算方法.
二.由长方体(直四棱柱)的体积公式:V
=
S×h
.
对于一般的棱柱其体积的计算方法是怎样的呢
问题的提出:
新课讲解
一.介绍(祖暅原理)的具体内容:
我国古代数学家祖暅在“开立圆术”一书中指出:
(约在公元5世纪)
“夫叠棊(棋)成立积,缘幂势既同,则积不容异”
现代文解释为:
体积可以看成是由面积叠加而成,用一组平行的平面截两个空间图形,若在任意高处的截面面积都对应相等,则两个空间图形的体积必然相等.
说明
①上述论述称为祖暅原理,其正确性可以验证.
②利用叠书法加以理解和感悟.
祖暅原理
S
h
S
S
h
新课讲解
二.棱柱体积公式的推导:
由长方体的体积公式V=S×h.利用祖暅原理,结合推导出:
(棱柱体积公式)--
V棱柱=
S×h
.
新课讲解
例题1
三.棱柱体积的计算.
已知三棱柱
的底面为直角三角形,两直角边AC和BC的长分别为4cm和3cm,侧棱
的长为10cm,求满足下列条件的三棱柱的体积.
(1)侧棱
垂直于底面;
(2)侧棱
与底面所成的角为60°.
例题1
已知三棱柱
的底面为直角三角形,两直角边AC和BC的长分别为4cm和3cm,侧棱
的长为10cm,求满足下列条件的三棱柱的体积.
(1)侧棱
垂直于底面;
(2)侧棱
与底面所成的角为60°.
例题1
已知三棱柱
的底面为直角三角形,两直角边AC和BC的长分别为4cm和3cm,侧棱
的长为10cm,求满足下列条件的三棱柱的体积.
(1)侧棱
垂直于底面;
(2)侧棱
与底面所成的角为60°.
归纳总结
①计算棱柱体积,关键是计算棱柱的底面积和棱柱的高.
②为方便计算棱柱的底面积,可以把棱柱的底面多边形画成其平面图形.
③注意区分棱柱的侧棱与棱柱的高之间的区别.
在直棱柱中:
侧棱=高;
而在一般的斜棱柱中:侧棱与高并不相等,但侧棱与高加上侧棱在底面上的射影构成一个Rt△.
