3.1.2函数的表示法 课件(共26张PPT)
文档属性
| 名称 | 3.1.2函数的表示法 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 09:34:53 | ||
图片预览




文档简介
(共26张PPT)
3.1.2函数的表示法
2019人教A版
必修一
函数的定义
设A、B是非空数集,如果按照
某种确定的对应关系
f,使对于集
合A中的任意一个数
x,在集合B中
都有唯一确定的数
f(x)
和它对应,
就称f:
A→B
为从集合A到集合
B的一个函数,记作:
y=f(x)
,
x∈A
区间的概念
新知导入
复习巩固
新知导入
解(1)
(2)
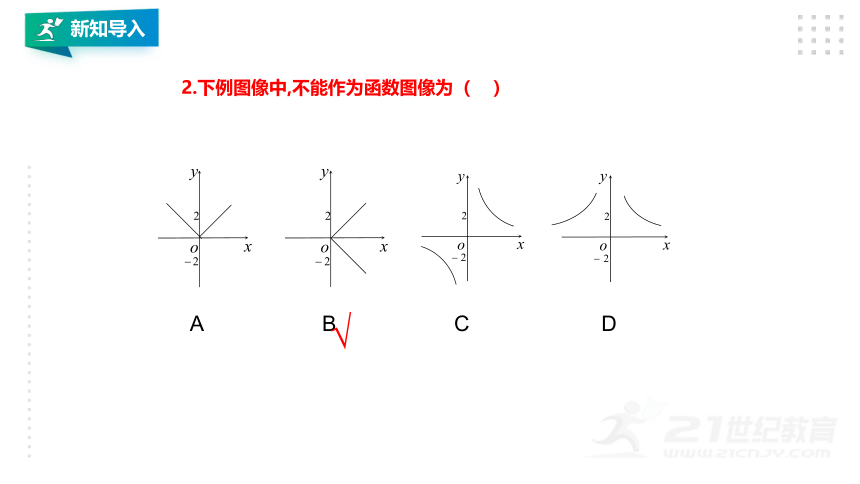
2.下例图像中,不能作为函数图像为(
)
A
B
C
D
新知导入
√
新知讲解
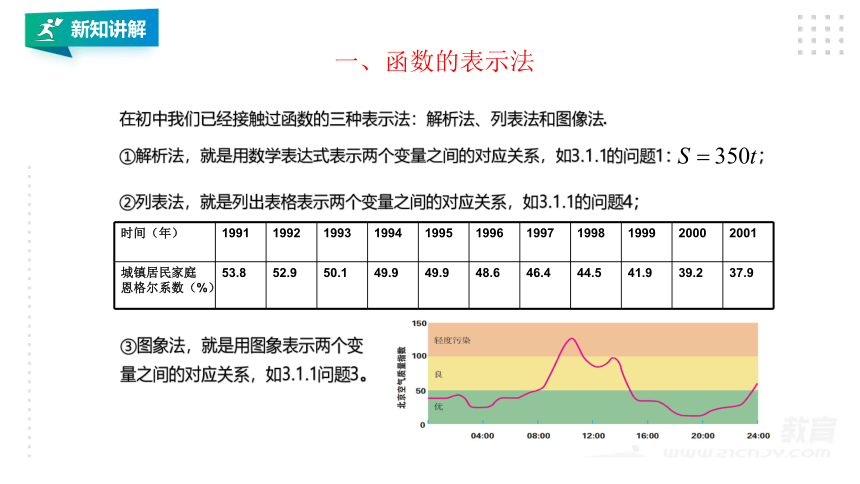
一、函数的表示法
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
城镇居民家庭恩格尔系数(%)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
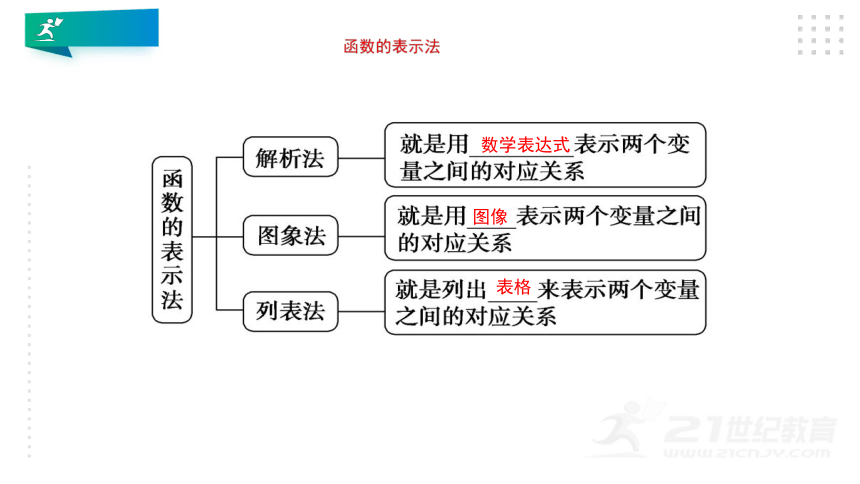
函数的表示法
数学表达式
图像
表格
新知讲解
同一函数问题多种表示方法
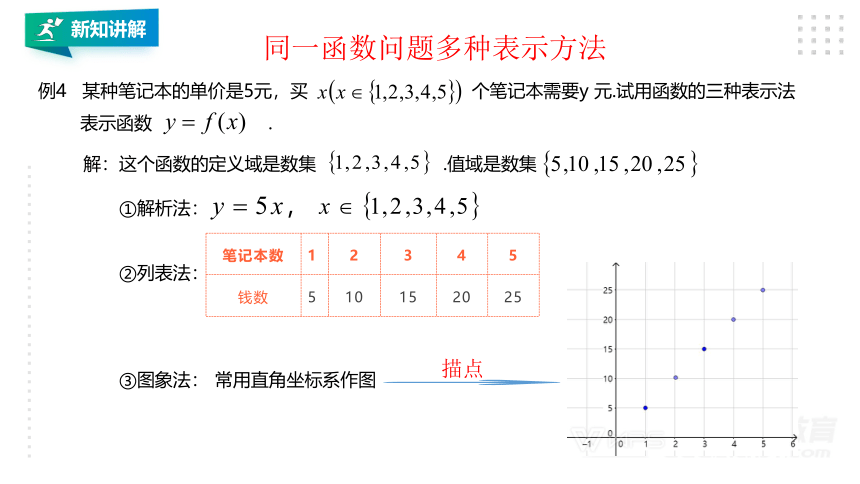
例4
某种笔记本的单价是5元,买
个笔记本需要y
元.试用函数的三种表示法
表示函数
.
解:这个函数的定义域是数集
.值域是数集
①解析法:
②列表法:
笔记本数
1
2
3
4
5
钱数
5
10
15
20
25
③图象法:
常用直角坐标系作图
描点
新知讲解
函数的三种表示法,它们各自的特点
解析法
对应关系清楚、简明,通过解析式可求出定义域内任意
自变量对应的函数值,便于研究函数性质.
列表法
不用计算,看表就知道函数值,但当自变量较多时,列表不易实现.
图象法
能形象、直观地表示出函数的变化情况,但求函数值比较困难,只能求近似值,且误差较大.
新知讲解
二、分段函数
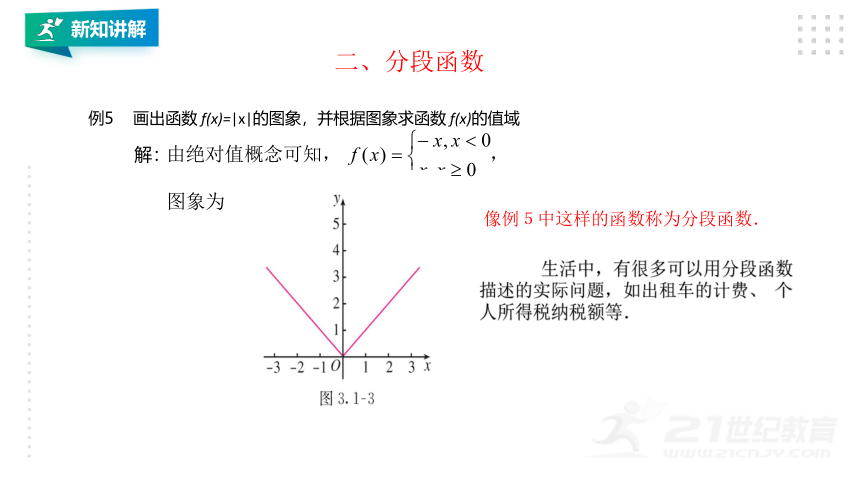
例5
画出函数
f(x)=|x|的图象,并根据图象求函数
f(x)的值域
解:
像例5中这样的函数称为分段函数.
新知讲解
(一)分段函数的概念
在自变量的不同取值区间,有不同对应关系的函数叫做分段函数.
注意:分段函数是一个函数,不是几个函数。定义域是各段自变量取值区间的并
集,值域是各段函数在对应自变量取值范围内值域的并集.
试一试,画出下列函数的图象并写出其定义域值域:
y=x2-2x(x>1,或x<-1)
定义域:
值域:
合作探究
结合图像
合作探究
合作探究
合作探究
1.函数f(x)的图象如图所示,则f(x)的定
义域是
,值域是
.
[-1,0)∪(0,2]
[-1,1)
2.已知分段函数
(1)求
;(2)画出函数图像,并求出定义域和值域。
解:(1)
同理
课堂练习
2.已知分段函数
(1)求
;(2)画出函数图像,并求出定义域和值域。
课堂练习
解:(2)定义域为R
,
当
时,
,先画出
的函数图象,如图:
同理,当
时,
先画出
的函数图像,如图,再取右边部分。
图象只取左边部分;
的图象如右图:
由图,函数的值域为
.
课堂练习
新知讲解
三、求函数解析式部分方法
1、待定系数法:已知函数的类型(如一次函数、二次函数),比如二次函数可设为f(x)=ax2+bx+c(a≠0),其
中a、b、c是待定系数,根据题设条件列出方程组,解出待定系数
解:设f(x)=kx+b(k≠0)
则f(f(x))=f(kx+b)
=k(kx+b)+b
=k2x+kb+b
=4x-1
新知讲解
2、配凑法.已知f(h(x))=g(x),求f(x)的问题,往往把右边的g(x)整理或配凑成只含h(x)的式子,用x将h(x)代换
例2.已知
,求(x)的解析式。
解:∵
新知讲解
3、换元法.已知f(h(x))=g(x),求f(x)时,往往可设h(x)=t,从中解出x,代入g(x)进行换元
举例解:例2中,令
4.解方程组法.已知f(x)满足某个等式,根据已知等式再构造其他等式组成方程组,通过解方程
组求出f(x).
例3已知函数f(x)满足
,求f(x)的解析式。
(3)由
得
,
联立得
①+②×2得f(x)=x+4f(x)+ ,
则f(x)=-
- x.
课堂练习
2、已知f(x+1)=x2+2x+2,求f(x)
解:
法一:配凑法
f(x+1)=x2+2x+2=(x+1)2+1,
∴f(x)=x2+1.
法二:换元法
令t=x+1
则x=t-1
f(t)=(t-1) +2(t-1)
=t -2t+1+2t-2
=t -1
∴f(x)=x2+1
√
课堂总结
1、函数的基本表示法(列表法、图象法、解析法)
2、描点法画一些简单函数的图象。
3、分段函数
4、求函数解析式的待定系数法、配凑法、换元法、消元法、
这节课我们学到了什么?
板书设计
函数的基本表示法
解析法
列表法
图象法
分段函数
定义
图像
求函数解析式
待定系数法
配凑法
换元法
消元法
作业布置
一、课本P72页,3、4、6、7
二、课本P73页,12、13
https://www.21cnjy.com/help/help_extract.php
3.1.2函数的表示法
2019人教A版
必修一
函数的定义
设A、B是非空数集,如果按照
某种确定的对应关系
f,使对于集
合A中的任意一个数
x,在集合B中
都有唯一确定的数
f(x)
和它对应,
就称f:
A→B
为从集合A到集合
B的一个函数,记作:
y=f(x)
,
x∈A
区间的概念
新知导入
复习巩固
新知导入
解(1)
(2)
2.下例图像中,不能作为函数图像为(
)
A
B
C
D
新知导入
√
新知讲解
一、函数的表示法
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
城镇居民家庭恩格尔系数(%)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
函数的表示法
数学表达式
图像
表格
新知讲解
同一函数问题多种表示方法
例4
某种笔记本的单价是5元,买
个笔记本需要y
元.试用函数的三种表示法
表示函数
.
解:这个函数的定义域是数集
.值域是数集
①解析法:
②列表法:
笔记本数
1
2
3
4
5
钱数
5
10
15
20
25
③图象法:
常用直角坐标系作图
描点
新知讲解
函数的三种表示法,它们各自的特点
解析法
对应关系清楚、简明,通过解析式可求出定义域内任意
自变量对应的函数值,便于研究函数性质.
列表法
不用计算,看表就知道函数值,但当自变量较多时,列表不易实现.
图象法
能形象、直观地表示出函数的变化情况,但求函数值比较困难,只能求近似值,且误差较大.
新知讲解
二、分段函数
例5
画出函数
f(x)=|x|的图象,并根据图象求函数
f(x)的值域
解:
像例5中这样的函数称为分段函数.
新知讲解
(一)分段函数的概念
在自变量的不同取值区间,有不同对应关系的函数叫做分段函数.
注意:分段函数是一个函数,不是几个函数。定义域是各段自变量取值区间的并
集,值域是各段函数在对应自变量取值范围内值域的并集.
试一试,画出下列函数的图象并写出其定义域值域:
y=x2-2x(x>1,或x<-1)
定义域:
值域:
合作探究
结合图像
合作探究
合作探究
合作探究
1.函数f(x)的图象如图所示,则f(x)的定
义域是
,值域是
.
[-1,0)∪(0,2]
[-1,1)
2.已知分段函数
(1)求
;(2)画出函数图像,并求出定义域和值域。
解:(1)
同理
课堂练习
2.已知分段函数
(1)求
;(2)画出函数图像,并求出定义域和值域。
课堂练习
解:(2)定义域为R
,
当
时,
,先画出
的函数图象,如图:
同理,当
时,
先画出
的函数图像,如图,再取右边部分。
图象只取左边部分;
的图象如右图:
由图,函数的值域为
.
课堂练习
新知讲解
三、求函数解析式部分方法
1、待定系数法:已知函数的类型(如一次函数、二次函数),比如二次函数可设为f(x)=ax2+bx+c(a≠0),其
中a、b、c是待定系数,根据题设条件列出方程组,解出待定系数
解:设f(x)=kx+b(k≠0)
则f(f(x))=f(kx+b)
=k(kx+b)+b
=k2x+kb+b
=4x-1
新知讲解
2、配凑法.已知f(h(x))=g(x),求f(x)的问题,往往把右边的g(x)整理或配凑成只含h(x)的式子,用x将h(x)代换
例2.已知
,求(x)的解析式。
解:∵
新知讲解
3、换元法.已知f(h(x))=g(x),求f(x)时,往往可设h(x)=t,从中解出x,代入g(x)进行换元
举例解:例2中,令
4.解方程组法.已知f(x)满足某个等式,根据已知等式再构造其他等式组成方程组,通过解方程
组求出f(x).
例3已知函数f(x)满足
,求f(x)的解析式。
(3)由
得
,
联立得
①+②×2得f(x)=x+4f(x)+ ,
则f(x)=-
- x.
课堂练习
2、已知f(x+1)=x2+2x+2,求f(x)
解:
法一:配凑法
f(x+1)=x2+2x+2=(x+1)2+1,
∴f(x)=x2+1.
法二:换元法
令t=x+1
则x=t-1
f(t)=(t-1) +2(t-1)
=t -2t+1+2t-2
=t -1
∴f(x)=x2+1
√
课堂总结
1、函数的基本表示法(列表法、图象法、解析法)
2、描点法画一些简单函数的图象。
3、分段函数
4、求函数解析式的待定系数法、配凑法、换元法、消元法、
这节课我们学到了什么?
板书设计
函数的基本表示法
解析法
列表法
图象法
分段函数
定义
图像
求函数解析式
待定系数法
配凑法
换元法
消元法
作业布置
一、课本P72页,3、4、6、7
二、课本P73页,12、13
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
