1.3怎样描述速度变化的快慢

(共43张PPT)
复习回顾“速度”
速度的物理意义：
速度的定义、
大小和方向：
位移对时间的变化率
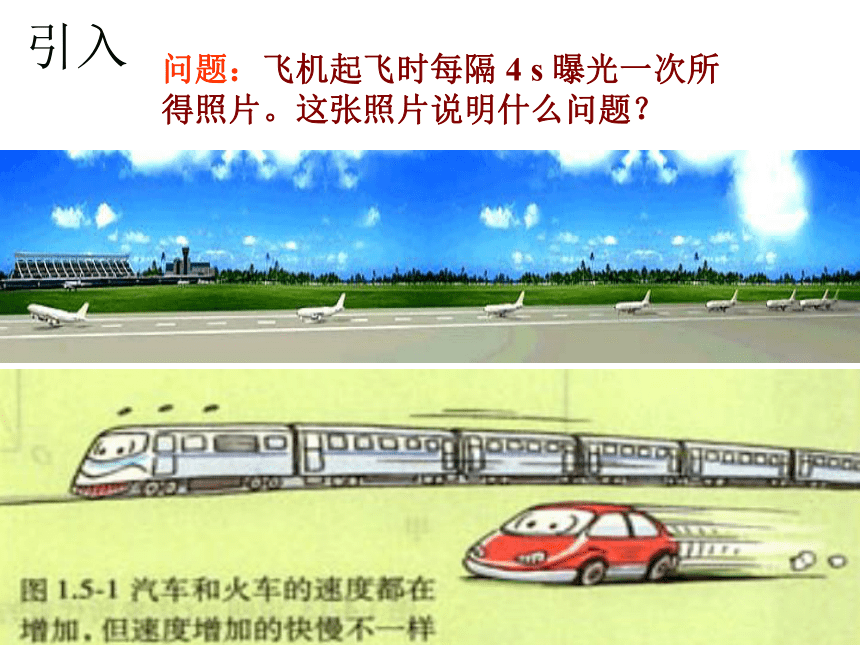
问题：飞机起飞时每隔 4 s 曝光一次所得照片。这张照片说明什么问题？
引入
随着生活水平的提高，许多家庭都有购车的计划，人们需对汽车的性能、价格等作出综合判断。
汽车的启动、制动性能是重要的指标。
如何比较不同汽车的启动、制动性能呢？
跑车加速性能的比较
观察
比较速度变化快慢
相同的时间内,速度变化大的速度变化快
相同的速度变化,用时越少速度变化越快
如何比较１和３谁的速度变化快呢？
速度的变化（量）
＋
v1
v2
△v=7m/s2
v1
v2
△v=-9m/s2
·
v1
v2
△v=-25m/s2
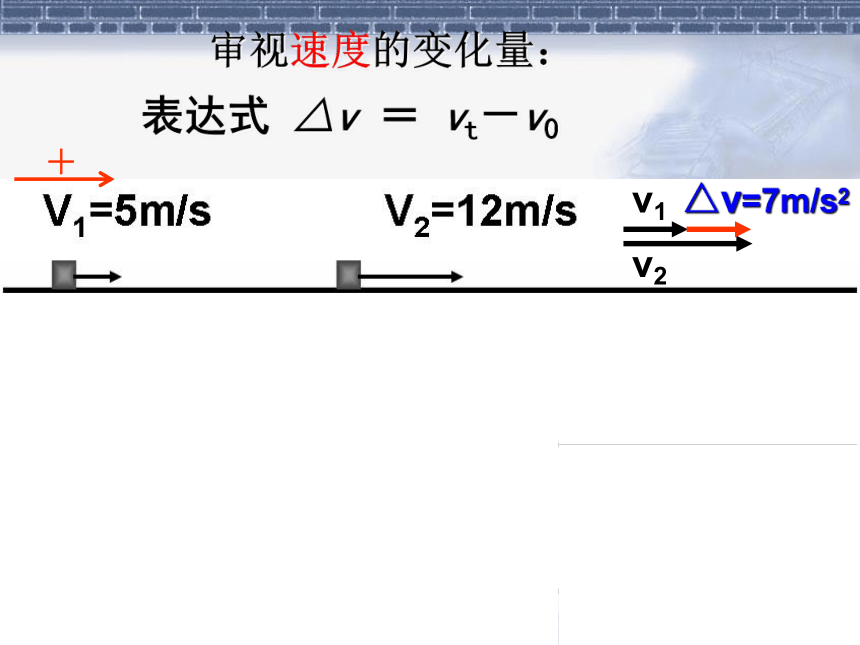
审视速度的变化量：
表达式 △v ＝ vt－v0
审视速度的变化 △v
（1）表达式 △v ＝ vt－v0
（2）△v ：矢量，有方向
加速运动， △v 和初速度同向，为正值；
减速运动， △v 和初速度反向，为负值
规定正方向：一般取初速度的方向为正方向
体会： △v 也有方向，
正负号的含义
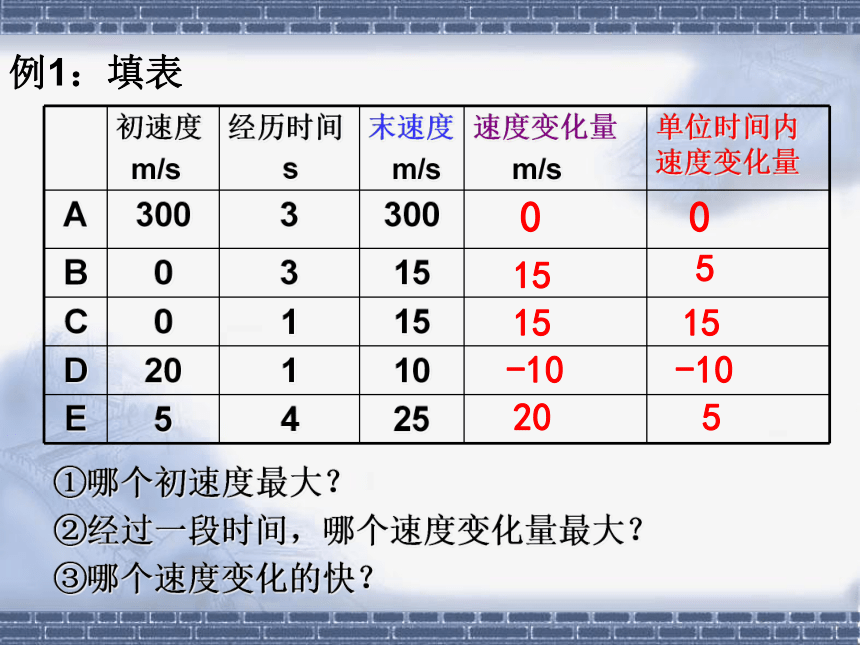
例1：填表
初速度
m/s 经历时间
s 末速度
m/s 速度变化量
m/s 单位时间内速度变化量
A 300 3 300
B 0 3 15
C 0 1 15
D 20 1 10
E 5 4 25
0
0
15
5
15
15
-10
-10
①哪个初速度最大？
②经过一段时间，哪个速度变化量最大？
③哪个速度变化的快？
20
5
物体速度变化快慢与物体速度的大小无关；与速度变化量的大小无关；只与单位时
间内速度的变化量有关，即：取决于
规定正方向：一般取初速度的方向为正方向
确定初、末速度的正负号：
方向跟正方向相同的取正号
方向跟正方向相反的取负号
一维情况下，把矢量运算简化为标量运算
足球以12m/s的速度与墙壁相碰后，以8m/s的速度反向弹回，球与墙的接触时间为0.1s，求足球的速度变化的大小和方向。
解：设初速度方向为正方向，即指向墙为正方向
所以足球的速度改变大小为20m/s，方向指向足球被反弹的方向。
则：v0=12m/s, vt=-8m/s t=0.1s

思维体操
描述变速运动，比较变速运动，需要哪些物理量？
位移、时间、
初速度、末速度、平均速度、
速度的变化、
¨¨¨
够了吗
必须引入新的物理量！
描述什么？如何定义？
许多物体做变速直线运动时，速度变化的快慢往往不同
为了描述物体运动速度变化的快慢，物理学中引入新的物理量
加速度
矢量
类比速度给加速度下定义
位置变化的快慢
速度变化的快慢
位置的改变
位移的变化率
单位：复合单位 ※
速度对时间的变化率
运动物体速度的变化跟发生这一变化所用时间的比值叫加速度
用来描述物体运动速度改变的快慢
单位时间内速度的改变量
规定 正方向：一般取初速度方向为正方向
判断 初、末速度的正负号
代人加速度定义式计算
加速度的方向
△v
v0
vt
△v
v0
vt
加速度的方向与速度变化量△v 的方向相同
a
a
物体作直线运动：当加速度与初速度方向相同时，物体做加速运动。当加速度与初速度方向相反时，物体做减速运动。
若规定v0方向为正方向（ v0> 0），
加速：a>0; 减速a<0
飞机起飞时，在大约30s内，速度由0增加到约300Km/h
[83m/s]
迫击炮在射击时，炮弹在炮筒中的速度在0.005s内就可以由0增加到250m/s
炮弹速度的变化，比飞机起飞速度的变化快得多！
体验加速度的方向：
足球以12m/s的速度与墙壁相碰后，以8m/s的速度反向弹回，球与墙的接触时间为0.1s，求足球加速度的大小和方向。
解：设初速度方向为正方向，即指向墙为正方向
所以足球的加速度大小为200m/s2，方向指向足球被反弹的方向。
则：v0=12m/s, vt=-8m/s t=0.1s
北京时间9月23日，2006年上海黄金大奖赛结束焦点战110栏的争夺，中国飞人刘翔以13秒07力挫劲敌阿兰-约翰逊夺得冠军成功卫冕。
研究人员对刘翔110米栏夺冠全过程进行了研究分析，由于情况比较复杂. 我们取三个运动的阶段:
第一个阶段：从起跑到起跑后到达第一个栏时，速度由零增加到9.53m/s，共用时间2.421s；
第二阶段：从第八个栏到第十个栏时，速度由9.32m/s减小到8.81m/s,共用时间2.062s；
第三阶段：最后的冲刺阶段，速度由8.81m/s增加到9.55m/s，共用时间1.507s。
请计算各个阶段的加速度分别为多少？(结果取两位有效数字。）
例题1：
速度:
速度的变化:
加速度（速度对时间的变化率）:
区别
⑴速度大，加速度不一定大；
加速度大, 速度不一定大。
⑵加速度为零，速度不一定为零;
速度为零，加速度也不一定为零
2、加速度和速度的区别
①它们的含义不同
速度描述的是位置变化的快慢
加速度描述的是速度变化的快慢
②看它们的大小情况
加速度大小和速度大小没必然联系；但 若a不为零，V一定变化
加速度 a = ( vt - v0 ) / t
某一物理量的变化跟发生这一变化所用的时间的比值，叫做该量对时间的变化率。加速度是速度对时间的 变化率
3、加速度和速度的变化量（Δv = vt - vo）：
速度的变化量表示速度改变了多少。等于物体末速度和初速度的矢量差（也为 矢量）.
所以：速度变化量大，加速度不一定大;
a 与Δv 也无直接联系
匀变速直线运动
计算出飞机在第一个10S内，第二个10S内，第三个10S内的
加速度大小为-------，并判断出加速度的方向是-------。
飞机在加速运动过程中的加速度大小和方向都保持不变
飞机在减速运动过程中加速度大小和方向都保持不变
物体做变速直线运动时，如果加速度大小和方向都保持不变，
就叫做匀变速直线运动
单位时间内速度的改变量不变
均匀增大 匀加速直线运动
均匀减小 匀减速直线运动
物体运动的速度在均匀变化：
例如：匀加速直线运动
a=2m/s2: 0， 2， 4， 6， 8， 10， 12，……
第一秒
第二秒
第三秒
第四秒
第五秒
第六秒
后一秒比前一秒增大2m/s
每一秒末比每一秒初增大2m/s
第n秒比第m秒增大（n—m)a
第n秒末比第m秒初增大（n—m+1)a
每秒内增大2m/s
任意相等时间内速度的改变量相同
匀变速直线运动是理想化运动模型
一物体从静止开始做直线运动，每秒末的速度为：
2， 4， 6， 8， 10， 12，……
请判断此物体是否做匀加速直线运动？为什么？
不一定
任意相等时间内速度 改变量相同
匀变速直线运动中，所有的矢量方向都在一条直线上，通常选取物体初速度v0的方向为正方向,于是：
匀减速直线运动
a﹤0 (表示a的方向与v0的方向相反)
匀加速直线运动
a﹥0 (表示a的方向与v0的方向相同)
小试牛刀
2.如图所示是一个物体向东运动的速度图象.由图可知在0~10s内物体的加速度大小是 , 方向是 ,在10~40s内物体的加速度大小是 ,在40~60s内物体的加速度大小是 ,方向是 .
3m/s2
向东
0
1.5m/s2
向西
3 .关于速度，速度改变量，加速度，正确的说法是：
A、物体运动的速度改变量很大，它的加速度一定很大
B、速度很大的物体，其加速度可以很小，可以为零
C、某时刻物体的速度为零，其加速度不可能为零
D、加速度很大时，运动物体的速度一定很大
( B )