2021-2022学年八年级数学上册 华东师大版 14.1.1直角三角形三边的关系 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年八年级数学上册 华东师大版 14.1.1直角三角形三边的关系 同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 463.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 21:33:23 | ||
图片预览



文档简介
2021-2022学年八年级数学上册(华东师大版)
14.1.1直角三角形三边的关系-同步练习
时间:60分钟
一、单选题
1.直角三角形中一直角边的长为18,另两边长为连续偶数,则直角三角形的周长为(
).
A.242
B.240
C.180
D.不能确定
2.下列说法正确的是(
)
A.若a、b、c是△ABC的三边,则a2b2c2;
B.若a、b、c是Rt△ABC的三边,则a2b2c2;
C.若a、b、c是Rt△ABC的三边,∠A=90°,则a2b2c2;
D.若a、b、c是Rt△ABC的三边,∠C=90°,则a2b2c2;
3.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4
B.3
C.4.5
D.5
4.已知中,,若,,则的面积是(
).
A.
B.
C.
D.
5.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是()
A.CD、EF、GH
B.AB、EF、GH
C.AB、CD、GH
D.AB、CD、EF
6.如果3,a,5是勾股数,则a的值是( )
A.4
B.
C.4或
D.4或34
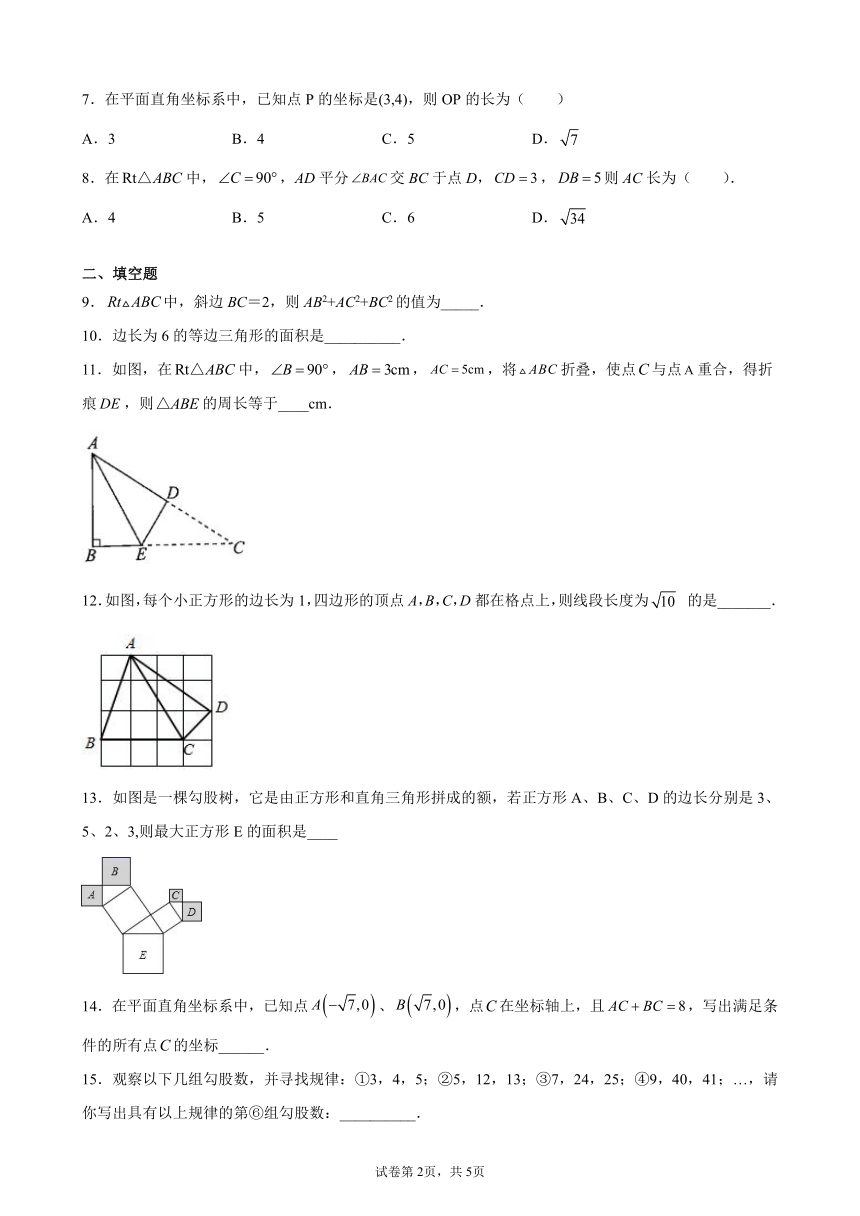
7.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为(
)
A.3
B.4
C.5
D.
8.在中,,AD平分交BC于点D,,则AC长为(
).
A.4
B.5
C.6
D.
二、填空题
9.中,斜边BC=2,则AB2+AC2+BC2的值为_____.
10.边长为6的等边三角形的面积是__________.
11.如图,在中,,,,将折叠,使点与点重合,得折痕,则的周长等于____cm.
12.如图,每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则线段长度为
的是_______.
13.如图是一棵勾股树,它是由正方形和直角三角形拼成的额,若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是____
14.在平面直角坐标系中,已知点、,点在坐标轴上,且,写出满足条件的所有点的坐标______.
15.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:__________.
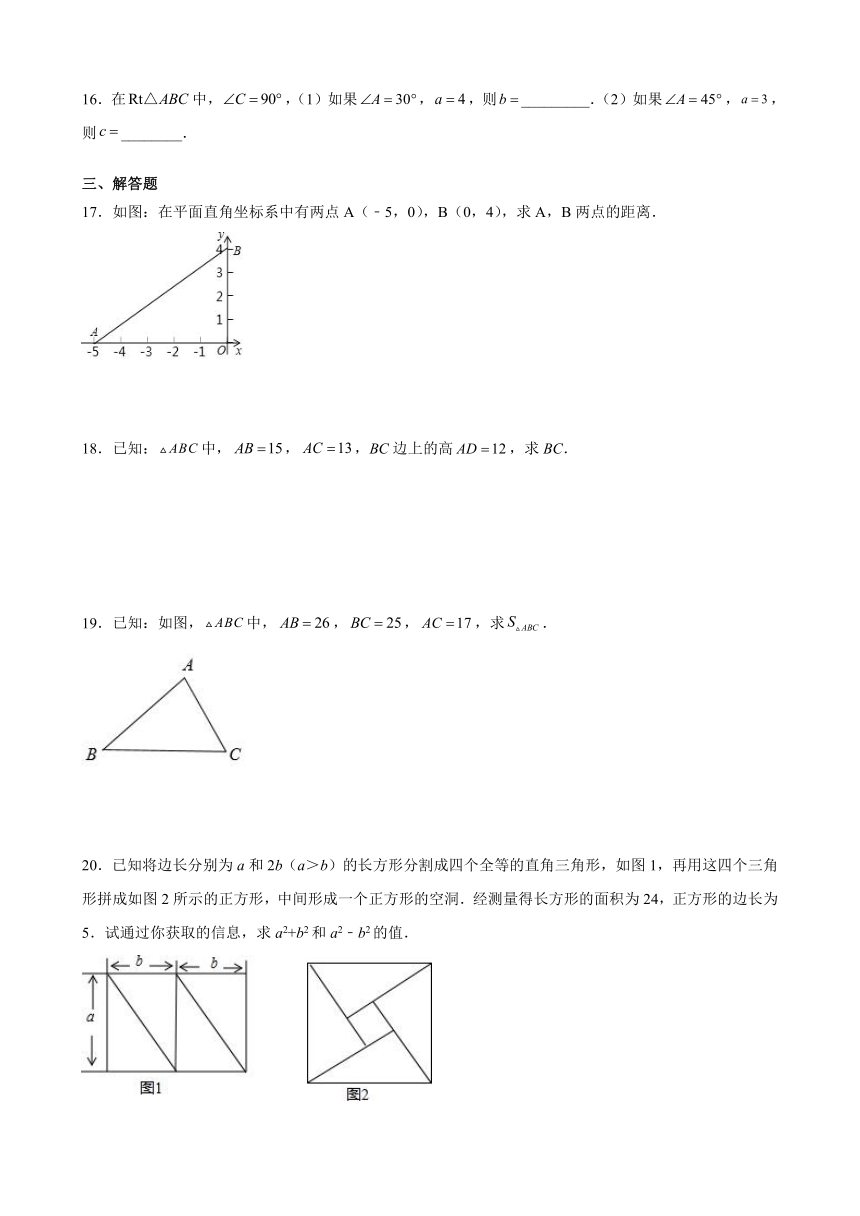
16.在中,,(1)如果,,则_________.(2)如果,,则________.
三、解答题
17.如图:在平面直角坐标系中有两点A(﹣5,0),B(0,4),求A,B两点的距离.
18.已知:中,,,BC边上的高,求BC.
19.已知:如图,中,,,,求.
20.已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
21.如图所示,有一个直角三角形纸片,两直角边,,现将直角边沿直线折叠,使它落在斜边上且与重合,你能求出的长吗?
22.先观察图形(如图所示),然后回答问题:
(1)设每个小方格的边长是1,则正方形的面积是______,正方形的面积是______,正方形的面积是______.
(2)正方形,正方形,正方形的面积之间有何关系?你能发现、、的关系吗?
23.如图:四边形ABCD中,
AB=BC=,
,
DA=1,
且AB⊥CB于B.
试求:(1)∠BAD的度数;(2)四边形ABCD的面积.
24.(1)按规律填表:
4
6
8
…
…
3
8
15
…
…
5
10
17
…
…
(2)上表中,每列三个数为一组,这组数有什么特点?
(3)如果一个直角三角形的两条直角边长分别为20和99,你能很快得到斜边的长吗?
试卷第1页,共3页
参考答案
1.C
【解析】解:∵另两边长为连续偶数,
∴设另一条直角边为,则斜边为,
根据勾股定理得:
解得:,
∴直角三角形的另一条直角边是,斜边为,
直角三角形的周长为:,
故选:C.
2.D
【解析】A、勾股定理只限于在直角三角形里应用,故错误;
B、虽然给出的是直角三角形,但没有给出哪一个是直角,故B错误;
C、在Rt△ABC中,直角所对的边是斜边,C中的斜边应为a,得出的表达式应为b2+c2=a2,故C也错误;
D、符合勾股定理,正确.
故答案为:D.
3.A
【解析】解:∵点C′是AB边的中点,AB=6,
∴BC′=3,
由图形折叠特性知,C′F=CF=BC﹣BF=9﹣BF,
在Rt△C′BF中,BF2+BC′2=C′F2,
∴BF2+9=(9﹣BF)2,
解得,BF=4,
故选:A.
4.A
【解析】,
中,,
故选A
5.B
【解析】解:设小正方形的边长为1,
则AB2=22+22=8,
CD2=22+42=20,
EF2=12+22=5,
GH2=22+32=13.
因为AB2+EF2=GH2,
所以能构成一个直角三角形三边的线段是AB、EF、GH.
故选:B.
6.A
【解析】解:∵3,a,5是勾股数,∴或
∴a=(舍去
)或a=4
故选A.
7.C
【解析】如图所示:
∵P(3,4),
∴OP==5.
故选C.
8.C
【解析】解:过作,垂足为
∵为角平分线,,
∴
∵,
∴
∴
在中,
∴
∴整理可得:
∴
解得:
故选:
9.8
【解析】∵中,BC为斜边,且,
∴,
∴,
故答案为:8.
10.
【解析】如图,在中,作,
故答案为:.
11.7
【解析】在中,,,,由勾股定理,得,由翻折的性质,得,的周长为7(cm).
12.AB
【解析】解:由勾股定理可得:,BC=3,,,
故长度为是AB,
故答案为AB.
13.47
【解析】解:如图所示:
∵正方形A、B、C、D的边长分别是3、5、2、3,
∴正方形A、B、C、D的面积分别是32=9,52=25,22=4,32=9,
∵∠GFH=90°,
∴GH2=GF2+FH2=9+25=34,
∴正方形GHMN的面积=34,
同理:正方形MKLS的面积=4+9=13,
同理:正方形E的面积=34+13=47;
故答案为:47
14.,,,
【解析】解:①当点C位于x轴上时,设点C坐标为(x,0),则,解得x=4或x=-4;
②当点C在y轴上时,由勾股定理得,解得y=±3
综上所述,满足条件的所有点C的坐标为(4,0)(-4,0)(0,3)(0,-3)
15.13,84,85
【解析】由题意得,每组第一个数是奇数,且逐步递增2,第二、第三个数相差为一
故第⑥组的第一个数是13
设第二个数为x,第三个数为x+1
根据勾股定理得
解得
则第⑥组勾股数:13,84,85
故答案为:13,84,85.
16.(1);
(2)
【解析】解:在中,,则为斜边;
(1)∵,,
∴,
∴;
故答案为:;
(2)∵,,
∴,
∴;
故答案为:.
17.
【解析】解:AO=5,BO=4,
由勾股定理得:.
18.4或14
【解析】解:①∵在Rt△ABD中,
∴BD=,
在Rt△ADC中,CD=,
故BC=BD+CD=14;
②在Rt△ABD中,
BD=,
在Rt△ADC中,CD=,
故BC=BD CD=4,
∴BC的长为或4或14.
19.204
【解析】作于D,设,则,
在Rt△ABD中,Rt△BCD中有
∴
即:,
∴,
∵
∴,
∴.
故答案为:204.
20.a2+b2=25,a2﹣b2=7.
【解析】解:根据题意得
a2+b2=52=25,
a 2b=24,
∴a2+b2+2ab=49,
∴a+b=7,
由图2得(a-b)2=52-24=1,
∵a>b,
∴a-b=1,
∴a2﹣b2=(a+b)(a-b)=7×1=7,
∴a2+b2=25,a2﹣b2=7.
21.3
【解析】在三角形ABC中,由勾股定理可知:
.
由折叠的性质可知:
,,.
∴,.
设,则.
在中,由勾股定理得:
,即.
解得:.
∴.
22.(1)1,1,2;(2)正方形的面积+正方形的面积=正方形的面积..
【解析】解:(1)根据题意,可得:
正方形的面积=,
正方形的面积=,
正方形的面积=;
故答案为:1,1,2.
(2)由(1)知,,
∴正方形的面积+正方形的面积=正方形的面积;
∵正方形的面积=,正方形的面积=,正方形的面积=,
∴.
23.(1)135°(2)2
【解析】(1)连接AC,∵AB=BC=,
∴AC=
∴∠BAC=45°,
∵AD2+AC2=1+4=5=CD2,
∴△ACD为直角三角形.
∴∠BAD=90°+45°=135°,
(2)S四边形ABCD=S△ABC+
S△ADC==1+1=2
24.(1),;(2)都是勾股数;(3).
【解析】(1)由图表可以得出:
4=2×2,3=22-1,5=22+1,
6=2×3,8=32-1,10=32+1,
8=2×4,15=42-1,17=42+1,
…
∴2n,n2-1,n2+1.
(2)由表可得:每一列的三个数组成了勾股数.
(3)∵一个直角三角形的两条直角边长分别为20和99,
∴斜边长为:.
答案第1页,共2页
答案第1页,共2页
14.1.1直角三角形三边的关系-同步练习
时间:60分钟
一、单选题
1.直角三角形中一直角边的长为18,另两边长为连续偶数,则直角三角形的周长为(
).
A.242
B.240
C.180
D.不能确定
2.下列说法正确的是(
)
A.若a、b、c是△ABC的三边,则a2b2c2;
B.若a、b、c是Rt△ABC的三边,则a2b2c2;
C.若a、b、c是Rt△ABC的三边,∠A=90°,则a2b2c2;
D.若a、b、c是Rt△ABC的三边,∠C=90°,则a2b2c2;
3.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4
B.3
C.4.5
D.5
4.已知中,,若,,则的面积是(
).
A.
B.
C.
D.
5.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是()
A.CD、EF、GH
B.AB、EF、GH
C.AB、CD、GH
D.AB、CD、EF
6.如果3,a,5是勾股数,则a的值是( )
A.4
B.
C.4或
D.4或34
7.在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为(
)
A.3
B.4
C.5
D.
8.在中,,AD平分交BC于点D,,则AC长为(
).
A.4
B.5
C.6
D.
二、填空题
9.中,斜边BC=2,则AB2+AC2+BC2的值为_____.
10.边长为6的等边三角形的面积是__________.
11.如图,在中,,,,将折叠,使点与点重合,得折痕,则的周长等于____cm.
12.如图,每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则线段长度为
的是_______.
13.如图是一棵勾股树,它是由正方形和直角三角形拼成的额,若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是____
14.在平面直角坐标系中,已知点、,点在坐标轴上,且,写出满足条件的所有点的坐标______.
15.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:__________.
16.在中,,(1)如果,,则_________.(2)如果,,则________.
三、解答题
17.如图:在平面直角坐标系中有两点A(﹣5,0),B(0,4),求A,B两点的距离.
18.已知:中,,,BC边上的高,求BC.
19.已知:如图,中,,,,求.
20.已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
21.如图所示,有一个直角三角形纸片,两直角边,,现将直角边沿直线折叠,使它落在斜边上且与重合,你能求出的长吗?
22.先观察图形(如图所示),然后回答问题:
(1)设每个小方格的边长是1,则正方形的面积是______,正方形的面积是______,正方形的面积是______.
(2)正方形,正方形,正方形的面积之间有何关系?你能发现、、的关系吗?
23.如图:四边形ABCD中,
AB=BC=,
,
DA=1,
且AB⊥CB于B.
试求:(1)∠BAD的度数;(2)四边形ABCD的面积.
24.(1)按规律填表:
4
6
8
…
…
3
8
15
…
…
5
10
17
…
…
(2)上表中,每列三个数为一组,这组数有什么特点?
(3)如果一个直角三角形的两条直角边长分别为20和99,你能很快得到斜边的长吗?
试卷第1页,共3页
参考答案
1.C
【解析】解:∵另两边长为连续偶数,
∴设另一条直角边为,则斜边为,
根据勾股定理得:
解得:,
∴直角三角形的另一条直角边是,斜边为,
直角三角形的周长为:,
故选:C.
2.D
【解析】A、勾股定理只限于在直角三角形里应用,故错误;
B、虽然给出的是直角三角形,但没有给出哪一个是直角,故B错误;
C、在Rt△ABC中,直角所对的边是斜边,C中的斜边应为a,得出的表达式应为b2+c2=a2,故C也错误;
D、符合勾股定理,正确.
故答案为:D.
3.A
【解析】解:∵点C′是AB边的中点,AB=6,
∴BC′=3,
由图形折叠特性知,C′F=CF=BC﹣BF=9﹣BF,
在Rt△C′BF中,BF2+BC′2=C′F2,
∴BF2+9=(9﹣BF)2,
解得,BF=4,
故选:A.
4.A
【解析】,
中,,
故选A
5.B
【解析】解:设小正方形的边长为1,
则AB2=22+22=8,
CD2=22+42=20,
EF2=12+22=5,
GH2=22+32=13.
因为AB2+EF2=GH2,
所以能构成一个直角三角形三边的线段是AB、EF、GH.
故选:B.
6.A
【解析】解:∵3,a,5是勾股数,∴或
∴a=(舍去
)或a=4
故选A.
7.C
【解析】如图所示:
∵P(3,4),
∴OP==5.
故选C.
8.C
【解析】解:过作,垂足为
∵为角平分线,,
∴
∵,
∴
∴
在中,
∴
∴整理可得:
∴
解得:
故选:
9.8
【解析】∵中,BC为斜边,且,
∴,
∴,
故答案为:8.
10.
【解析】如图,在中,作,
故答案为:.
11.7
【解析】在中,,,,由勾股定理,得,由翻折的性质,得,的周长为7(cm).
12.AB
【解析】解:由勾股定理可得:,BC=3,,,
故长度为是AB,
故答案为AB.
13.47
【解析】解:如图所示:
∵正方形A、B、C、D的边长分别是3、5、2、3,
∴正方形A、B、C、D的面积分别是32=9,52=25,22=4,32=9,
∵∠GFH=90°,
∴GH2=GF2+FH2=9+25=34,
∴正方形GHMN的面积=34,
同理:正方形MKLS的面积=4+9=13,
同理:正方形E的面积=34+13=47;
故答案为:47
14.,,,
【解析】解:①当点C位于x轴上时,设点C坐标为(x,0),则,解得x=4或x=-4;
②当点C在y轴上时,由勾股定理得,解得y=±3
综上所述,满足条件的所有点C的坐标为(4,0)(-4,0)(0,3)(0,-3)
15.13,84,85
【解析】由题意得,每组第一个数是奇数,且逐步递增2,第二、第三个数相差为一
故第⑥组的第一个数是13
设第二个数为x,第三个数为x+1
根据勾股定理得
解得
则第⑥组勾股数:13,84,85
故答案为:13,84,85.
16.(1);
(2)
【解析】解:在中,,则为斜边;
(1)∵,,
∴,
∴;
故答案为:;
(2)∵,,
∴,
∴;
故答案为:.
17.
【解析】解:AO=5,BO=4,
由勾股定理得:.
18.4或14
【解析】解:①∵在Rt△ABD中,
∴BD=,
在Rt△ADC中,CD=,
故BC=BD+CD=14;
②在Rt△ABD中,
BD=,
在Rt△ADC中,CD=,
故BC=BD CD=4,
∴BC的长为或4或14.
19.204
【解析】作于D,设,则,
在Rt△ABD中,Rt△BCD中有
∴
即:,
∴,
∵
∴,
∴.
故答案为:204.
20.a2+b2=25,a2﹣b2=7.
【解析】解:根据题意得
a2+b2=52=25,
a 2b=24,
∴a2+b2+2ab=49,
∴a+b=7,
由图2得(a-b)2=52-24=1,
∵a>b,
∴a-b=1,
∴a2﹣b2=(a+b)(a-b)=7×1=7,
∴a2+b2=25,a2﹣b2=7.
21.3
【解析】在三角形ABC中,由勾股定理可知:
.
由折叠的性质可知:
,,.
∴,.
设,则.
在中,由勾股定理得:
,即.
解得:.
∴.
22.(1)1,1,2;(2)正方形的面积+正方形的面积=正方形的面积..
【解析】解:(1)根据题意,可得:
正方形的面积=,
正方形的面积=,
正方形的面积=;
故答案为:1,1,2.
(2)由(1)知,,
∴正方形的面积+正方形的面积=正方形的面积;
∵正方形的面积=,正方形的面积=,正方形的面积=,
∴.
23.(1)135°(2)2
【解析】(1)连接AC,∵AB=BC=,
∴AC=
∴∠BAC=45°,
∵AD2+AC2=1+4=5=CD2,
∴△ACD为直角三角形.
∴∠BAD=90°+45°=135°,
(2)S四边形ABCD=S△ABC+
S△ADC==1+1=2
24.(1),;(2)都是勾股数;(3).
【解析】(1)由图表可以得出:
4=2×2,3=22-1,5=22+1,
6=2×3,8=32-1,10=32+1,
8=2×4,15=42-1,17=42+1,
…
∴2n,n2-1,n2+1.
(2)由表可得:每一列的三个数组成了勾股数.
(3)∵一个直角三角形的两条直角边长分别为20和99,
∴斜边长为:.
答案第1页,共2页
答案第1页,共2页
