沪教版(上海)数学高三上册-16.3 计数原理II——加法原理_(课件)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.3 计数原理II——加法原理_(课件) |

|
|
| 格式 | ppt | ||
| 文件大小 | 336.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 00:00:00 | ||
图片预览




文档简介
(共10张PPT)
计数原理II---加法原理
1.
通过实例,学习和掌握计数原理II----分类加法原理,
2.区分分步与分类的差别,理解乘法与加法原理的异同点,掌握解决计数问题的最基本方法:“枚举法”或“树型图”在乘法和加法原理中的区别
3.
利用加法原理解决简单的实际问题
教学目标:
一.引入
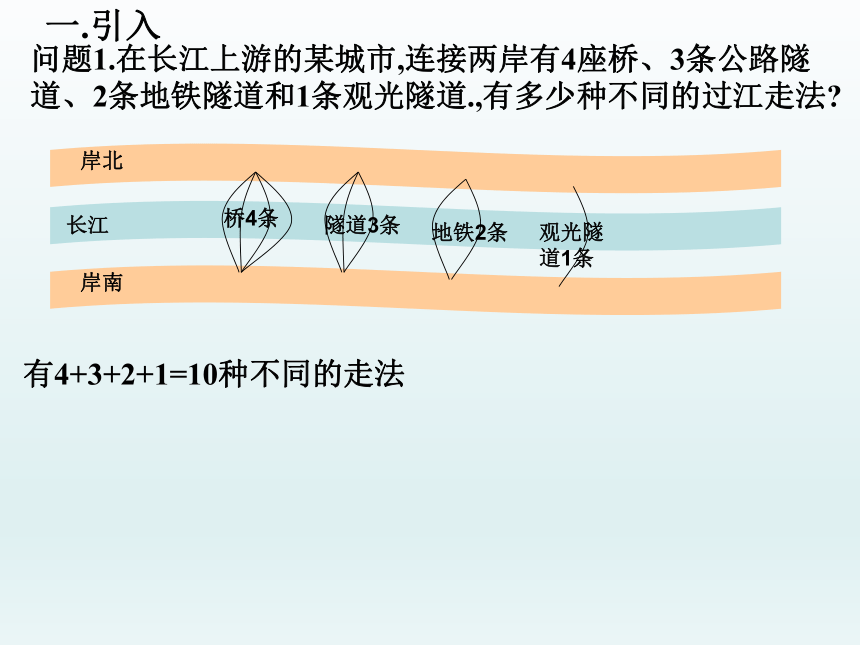
问题1.在长江上游的某城市,连接两岸有4座桥、3条公路隧道、2条地铁隧道和1条观光隧道.,有多少种不同的过江走法
长江
桥4条
隧道3条
地铁2条
观光隧道1条
岸北
岸南
有4+3+2+1=10种不同的走法
二.分类加法原理:
③“类与类”之间是“或”的关系;
而“步与步”之间是“且”的关关系;
“分类加法”原理:如果完成一件事需要n类办法,
在第1类办法中有m1种不同方法,在第2类办法中有m2种不同方法,
…
,在第n类办法中有mn种不同方法,那么完成这件事共有:
N=m1+m2+…+mn种不同办法.
“分类”理解:①类与类之间不能重复也不能遗漏;
②“分类”与“分步”的不同点:
“分类”中的每一类方法都能独立完成一件事;
“分步”中的每一部的方法都无法独立完成一件事;
④“分类”与“分步”的图示区别:完成“从A到B”事件
第1类
第2类
第n类
A
B
……
分类
分步
A
B
第1步
第2步
第n步
……
三.计数原理II—分类加法原理的简单应用
例1.从甲地到乙地可以乘火车,也可以乘汽车或轮船.如果一天中火车有6班、汽车有5班轮船有3班,那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法
解:由题意知:独立坐火车(或汽车或轮船)可以完成从甲到乙事件,故分三类:
共有6+5+3=14种走法.
火车6
汽车5
轮船3
甲
乙
分类
例2.用红黄蓝的小旗各一面挂在旗杆上表示信号,每次可以挂一面或二面或3三面,并且不同的顺序表示不同的信号,共可表示多少种不同的信号
解:N=P3
+
P3
+P3
=15种不同的信号
1
2
3
析:题意中出现的数字是一个四位数,其限制条件是首位是3~7之间的整数,末位是奇数的各位数上数字均不同.
完成四位奇数必须分二类:①首位是3~7的奇数;
②首位是3~7的偶数
例3.在3000到8000之间,有多少个没有重复数字的奇数
解:第①类首位选取的数是3,5,7之一的数有P3种,此时末位只能在余下4个奇数中选1个放末位
有P4种,
在余下8个数中选2个排放在十、百位上
有P8种,
∴有P3
P4
P8
种;
1
1
2
1
1
2
第②类首位选取的数是4,6之一的数有P2种,此时末位是5个奇数中选1个放末位
有P5种,
在余下8个数中选2个排放在十、百位上
有P8种,
∴有P2
P5
P8
种;
1
1
2
1
1
2
∴
P3
P4
P8
+
P2
P5
P8
=1232个
1
1
2
1
1
2
P8
2
P3
1
P4
1
P8
2
P2
1
P5
1
例4.
如果从7名运动员中选4名运动员组成接力队,参加4×100接力赛,那么甲、乙两人不跑中间两棒的安排方法有多少种
析:按照4名运动员中,
①含甲、乙两人;
②含甲、乙两人之一;
③不含甲、乙两人进行分类
解:①含甲、乙两人,但甲、乙两人不跑中间两棒有:P2
P5
种
2
2
②含甲、乙之一,但该人不跑中间两棒有:P2
P2
P5
种
1
1
3
③不含甲、乙,
有:P5
种
4
由加法原理得到:共有
P2
P5
+
P2
P2
P5
+
P5
=400种
1
2
1
2
3
4
中间两棒有:P5
2
中间两棒有:P5
3
③不含甲、乙的有P5
4
①甲、乙跑1、4棒有P2
2
②甲、乙之一跑1、4棒有P2
P2
1
1
例5.
用数字0、1、2、3、4、5可组成多少个无重复数字且比240135大的整数
析:按首位数字:比2大且小于等于5和等于2(再按次首位数字比4大或等于4分类;…)进行大分类;
解:1.首位 3的六位数有:P3
P5
1
5
2.首位=2的六位数分:
2
(1)次首位 5的六位数有:P1
P4
1
4
(2)次首位=4的六位数分:
4
此时千位数字若 1的六位数有:P3
P3
1
3
若=0的六位数分:
0
2
1
百位数字若 2的六位数有:P2
P2
1
百位数字若=1的六位数有:P1
1
3
由加法原理:P3
P5
+
P1
P4
+P3
P3
+P2
P2
+P1=407
1
4
1
1
1
1
5
2
例5.
用数字0、1、2、3、4、5可组成多少个无重复数字且比240135大的整数
析:采用排除法使解决问题的过程简化
∴符合题意的数有:P3
P5
+
P2
P4
-1
=407
1
5
1
4
◎善于观察,在24××××中,注意到0135是符合条件的四位数中最小数,换作其它的数,还是要按前面解法.
②首位是2,则第二位是4,5的数有P2
P4
=48;
1
4
2
其中要排除240135一个数,
4
解:①首位是3,4,5的六位数都符合题意
P3
1
P5
5
1
5
P3
P5
=360;
例6.
将a、b、c、d、e、f
六个不同元素排成一列
,
其中a不排在首位
,
b不排在末位,有几种排法
分析:
该问题有2个特殊元素,同时有2个特殊位置,应符合优先原则,先排.
注意:a不排在首位
,
a可排在末位,b同理
解:
①
a不在首位,a在末位,有:P5
5
a
②a不在首位且a不在末位,则a排放方法有:P4
,
1
1
再考虑元素b不在末位,
有:P4
,
其余元素的排放方法有:P4
4
∴符合题意排法有:P5
+
P4
P4
P4
=504
5
1
1
4
解二
(排除法):没有限制条件的排列有:P6
6
排除:a在首位的排列有:P5
5
b在末位的排列有:P5
5
排除过程中:a在首位且b在末位的排列重复的两次有:P4
4
∴符合条件排法有:P6
-2
P5
+
P4
=504
6
5
4
计数原理II---加法原理
1.
通过实例,学习和掌握计数原理II----分类加法原理,
2.区分分步与分类的差别,理解乘法与加法原理的异同点,掌握解决计数问题的最基本方法:“枚举法”或“树型图”在乘法和加法原理中的区别
3.
利用加法原理解决简单的实际问题
教学目标:
一.引入
问题1.在长江上游的某城市,连接两岸有4座桥、3条公路隧道、2条地铁隧道和1条观光隧道.,有多少种不同的过江走法
长江
桥4条
隧道3条
地铁2条
观光隧道1条
岸北
岸南
有4+3+2+1=10种不同的走法
二.分类加法原理:
③“类与类”之间是“或”的关系;
而“步与步”之间是“且”的关关系;
“分类加法”原理:如果完成一件事需要n类办法,
在第1类办法中有m1种不同方法,在第2类办法中有m2种不同方法,
…
,在第n类办法中有mn种不同方法,那么完成这件事共有:
N=m1+m2+…+mn种不同办法.
“分类”理解:①类与类之间不能重复也不能遗漏;
②“分类”与“分步”的不同点:
“分类”中的每一类方法都能独立完成一件事;
“分步”中的每一部的方法都无法独立完成一件事;
④“分类”与“分步”的图示区别:完成“从A到B”事件
第1类
第2类
第n类
A
B
……
分类
分步
A
B
第1步
第2步
第n步
……
三.计数原理II—分类加法原理的简单应用
例1.从甲地到乙地可以乘火车,也可以乘汽车或轮船.如果一天中火车有6班、汽车有5班轮船有3班,那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法
解:由题意知:独立坐火车(或汽车或轮船)可以完成从甲到乙事件,故分三类:
共有6+5+3=14种走法.
火车6
汽车5
轮船3
甲
乙
分类
例2.用红黄蓝的小旗各一面挂在旗杆上表示信号,每次可以挂一面或二面或3三面,并且不同的顺序表示不同的信号,共可表示多少种不同的信号
解:N=P3
+
P3
+P3
=15种不同的信号
1
2
3
析:题意中出现的数字是一个四位数,其限制条件是首位是3~7之间的整数,末位是奇数的各位数上数字均不同.
完成四位奇数必须分二类:①首位是3~7的奇数;
②首位是3~7的偶数
例3.在3000到8000之间,有多少个没有重复数字的奇数
解:第①类首位选取的数是3,5,7之一的数有P3种,此时末位只能在余下4个奇数中选1个放末位
有P4种,
在余下8个数中选2个排放在十、百位上
有P8种,
∴有P3
P4
P8
种;
1
1
2
1
1
2
第②类首位选取的数是4,6之一的数有P2种,此时末位是5个奇数中选1个放末位
有P5种,
在余下8个数中选2个排放在十、百位上
有P8种,
∴有P2
P5
P8
种;
1
1
2
1
1
2
∴
P3
P4
P8
+
P2
P5
P8
=1232个
1
1
2
1
1
2
P8
2
P3
1
P4
1
P8
2
P2
1
P5
1
例4.
如果从7名运动员中选4名运动员组成接力队,参加4×100接力赛,那么甲、乙两人不跑中间两棒的安排方法有多少种
析:按照4名运动员中,
①含甲、乙两人;
②含甲、乙两人之一;
③不含甲、乙两人进行分类
解:①含甲、乙两人,但甲、乙两人不跑中间两棒有:P2
P5
种
2
2
②含甲、乙之一,但该人不跑中间两棒有:P2
P2
P5
种
1
1
3
③不含甲、乙,
有:P5
种
4
由加法原理得到:共有
P2
P5
+
P2
P2
P5
+
P5
=400种
1
2
1
2
3
4
中间两棒有:P5
2
中间两棒有:P5
3
③不含甲、乙的有P5
4
①甲、乙跑1、4棒有P2
2
②甲、乙之一跑1、4棒有P2
P2
1
1
例5.
用数字0、1、2、3、4、5可组成多少个无重复数字且比240135大的整数
析:按首位数字:比2大且小于等于5和等于2(再按次首位数字比4大或等于4分类;…)进行大分类;
解:1.首位 3的六位数有:P3
P5
1
5
2.首位=2的六位数分:
2
(1)次首位 5的六位数有:P1
P4
1
4
(2)次首位=4的六位数分:
4
此时千位数字若 1的六位数有:P3
P3
1
3
若=0的六位数分:
0
2
1
百位数字若 2的六位数有:P2
P2
1
百位数字若=1的六位数有:P1
1
3
由加法原理:P3
P5
+
P1
P4
+P3
P3
+P2
P2
+P1=407
1
4
1
1
1
1
5
2
例5.
用数字0、1、2、3、4、5可组成多少个无重复数字且比240135大的整数
析:采用排除法使解决问题的过程简化
∴符合题意的数有:P3
P5
+
P2
P4
-1
=407
1
5
1
4
◎善于观察,在24××××中,注意到0135是符合条件的四位数中最小数,换作其它的数,还是要按前面解法.
②首位是2,则第二位是4,5的数有P2
P4
=48;
1
4
2
其中要排除240135一个数,
4
解:①首位是3,4,5的六位数都符合题意
P3
1
P5
5
1
5
P3
P5
=360;
例6.
将a、b、c、d、e、f
六个不同元素排成一列
,
其中a不排在首位
,
b不排在末位,有几种排法
分析:
该问题有2个特殊元素,同时有2个特殊位置,应符合优先原则,先排.
注意:a不排在首位
,
a可排在末位,b同理
解:
①
a不在首位,a在末位,有:P5
5
a
②a不在首位且a不在末位,则a排放方法有:P4
,
1
1
再考虑元素b不在末位,
有:P4
,
其余元素的排放方法有:P4
4
∴符合题意排法有:P5
+
P4
P4
P4
=504
5
1
1
4
解二
(排除法):没有限制条件的排列有:P6
6
排除:a在首位的排列有:P5
5
b在末位的排列有:P5
5
排除过程中:a在首位且b在末位的排列重复的两次有:P4
4
∴符合条件排法有:P6
-2
P5
+
P4
=504
6
5
4
