沪教版(上海)数学高三上册-16.4 组合 课件3(共54张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.4 组合 课件3(共54张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:36:11 | ||
图片预览











文档简介
(共54张PPT)
组合的综合应用
类型一
无限制条件的组合问题
【典型例题】
1.某人决定投资3种股票和4种债券,经纪人向他推荐了6种股票和5种债券,则此人不同的投资方式有______种.
2.某高中学生会由6名男生和4名女生组成.
(1)从中选4名学生参与学校卫生大检查,共有多少种不同的选法?
(2)从男生和女生中各选2名学生去“阳光敬老院”进行某项社会调查,共有多少种不同的选法?
【解题探究】
1.题1中投资需分几步?每步选法如何用组合数表示?
2.题2(2)中完成此件事需分几步走?分别是什么?
探究提示:
1.投资需分两步:第一步投资股票有
种,第二步,投资
债券有
种.
2.分两步走,第一步从6名男生中任选2名学生.第二步从4名
女生中任选2名学生.
【解析】1.需分两步:
第一步,根据经纪人的推荐在6种股票中选3种,共有
种选
法;
第二步,根据经纪人的推荐在5种债券中选4种,共有
种选
法.
根据分步乘法计数原理,此人有
种不同的投资方
式.
答案:100
2.(1)本问题相当于从10个不同的元素中,任取4个元素,所
以共有
种不同的选法.
(2)完成这件事分两步走:第一步从6名男生中任选2名学生,
共有
种不同的选法;第二步从4名女生中任选2
名学生,共有
种不同的选法.由分步乘法计数原
理得,共有15×6=90种不同的选法.
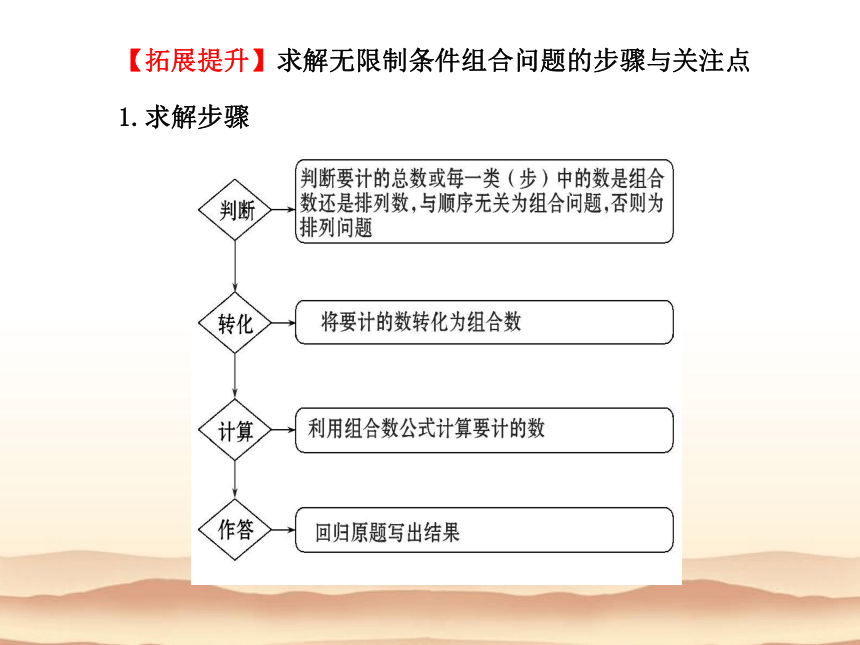
【拓展提升】求解无限制条件组合问题的步骤与关注点
1.求解步骤
2.关注点及注意点:要关注将要计的数是分类还是分步,在分类和分步时,一定要注意有无重复或遗漏.
【变式训练】(2013·成都高二检测)给一个正方体的六个面涂上四种不同颜色(红、黄、绿、蓝),要求相邻两个面涂不同的颜色,则共有涂色方法多少种(涂色后,任意翻转正方体,能使正方体各面颜色一致,我们认为是同一种涂色方法)(
)
A.6种
B.12种
C.24种
D.48种
【解析】选A.由于涂色过程中,要保证满足条件(用四种颜
色,相邻的面不同色),正方体的三对面,必然有两对同色,
一对不同色,而且三对面具有“地位对等性”,因此,只需
从四种颜色中选择2种涂在其中一对面上,剩下的两种颜色涂
在另外两对面即可.因此共有
(种)不同的涂法.
类型二
有限制条件的组合问题
【典型例题】
1.以正方体的顶点为顶点,可以确定______个四面体.
2.(2013·青岛高二检测)某医院从10名医疗专家中抽调6名奔赴灾区救灾,其中这10名医疗专家中有4名是外科专家.问:
(1)抽调的6名专家中恰有2名是外科专家的抽调方法有多少种?
(2)抽调的6名专家中至少有2名外科专家的抽调方法有多少种?
(3)抽调的6名专家中至多有2名外科专家的抽调方法有多少种?
【解题探究】
1.构成四面体的四个点需具备什么限制条件?
2.题2中“恰有2名外科专家”“至少有2名外科专家”与“至多有2名外科专家”的含义分别是什么?
探究提示:
1.构成四面体的四个点需具备不共面这一限制条件.
2.“恰有2名外科专家”指的是抽调的6名专家中有2名是外科专家,其余4名是非外科专家.
“至少有2名外科专家”指的是有可能是2名外科专家,也可能是3名或4名.
“至多有2名外科专家”指的是可能有2名外科专家,也可能1名或没有.
【解析】1.正方体8个顶点可构成
个四点组,其中共面的
四点组有正方体的6个表面的四个顶点和正方体相对棱分别所
在6个平面的四个顶点,故可以确定的四面体有
(个).
答案:58
2.(1)分步:首先从4名外科专家中任选2名,有
种选法,
再从除外科专家的6人中选取4人,有
种选法,所以共有
种抽调方法.
(2)“至少”的含义是不低于,有两种解答方法,
方法一(直接法):按选取的外科专家的人数分类:
①选2名外科专家,共有
种选法;
②选3名外科专家,共有
种选法;
③选4名外科专家,共有
种选法.
根据分类加法计数原理,共有
种抽调方法.
方法二(间接法):不考虑是否有外科专家,共有
种选法,
考虑选取1名外科专家参加,有
种选法;没有外科专家
参加,有
种选法,所以共有
种抽调方
法.
(3)“至多2名”包括“没有”“有1名”“有2名”三种情
况,分类解答.
①没有外科专家参加,有
种选法;
②有1名外科专家参加,有
种选法;
③有2名外科专家参加,有
种选法.
所以共有
种抽调方法.
【拓展提升】有限制条件的组合应用题的常见类型及求解思路
1.“含”与“不含”问题
这类问题的解题思路是将限制条件视为特殊元素和特殊位置,一般来讲,特殊要先满足,其余则“一视同仁”.若正面入手不易,则从反面入手,寻找问题的突破口,即采用间接法.解题时要注意分清“恰有”“有且仅有”“至多”“至少”“全是”“都不是”“不都是”等词语的确切含义,准确把握分类标准.
2.几何中的计数问题
在处理几何问题中的组合应用问题时,应先明确几何中的点、线、面及构型,明确平面图形和立体图形中的点、线、面之间的关系,将几何问题抽象成组合问题来解决.
【变式训练】1.在四棱锥P-ABCD中,顶点为P,从其他的顶点和各棱的中点中取3个,使它们和点P在同一平面内,不同的取法有(
)
A.40种
B.48种
C.56种
D.62种
【解析】选C.如图,
满足题设的取法可分为三类:
①在四棱锥的每个侧面上除
点P外任取3点,有
(种)不同的取法;
②在两个对角面上除点P外任取3点,共有
(种)不同
的取法;
③过点P的每一条棱上的三点和与这条棱异面的棱的中点也共
面,共有
(种)不同的取法.
故不同的取法共有40+8+8=56(种).
2.一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出3个球,共有多少种取法
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法
【解析】(1)
(种).
(2)从7个白球中任选2个,共有
(种).
(3)从7个白球中任选3个,共有
(种).
类型三
排列、组合的综合应用
【典型例题】
1.(2013·长春高二检测)某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数有(
)
A.6种
B.24种
C.180种
D.90种
2.(2013·安阳高二检测)从1到9的九个数字中取三个偶数四个奇数.试问:
(1)能组成多少个没有重复数字的七位数?
(2)上述七位数中三个偶数排在一起的有几个?
(3)(1)中的七位数中,偶数排在一起,奇数也排在一起的有几个?
(4)(1)中任意两个偶数都不相邻的七位数有几个?
【解题探究】
1.题1中的4名学生安排到两个班级是平均分组还是非平均分组 分组后还要分配吗?
2.题2(1)中组成没有重复数字的七位数,需要分几步完成?各是什么问题?
题2(2)中七位数中要求三个偶数排在一起,应如何安排?
题2(3)中的七位数应如何排?
题2(4)中的七位数应如何排?
探究提示:
1.是平均分组,且分组后需要分配.
2.组成题2(1)中的七位数,需分三步即第1步取3个偶数为组合问题,第二步取4个奇数为组合问题,第3步将取出的7个数排序,为排列问题.
题2(2)可用“捆绑法”安排.
题2(3)分别用“捆绑法”安排.
题2(4)可对偶数用插空法安排.
【解析】1.选D.先把4名学生分两组有
(种),然后
再把这两组给这6个班中的两个班有
(种),根据分步乘
法计数原理得不同的安排方案种数有3×30=90(种).
2.(1)分步完成:第一步在4个偶数中取3个,可有
种情
况;第二步在5个奇数中取4个,可有
种情况;第三步3
个偶数,4个奇数进行排列,可有
种情况,所以符合题
意的七位数有
(个).
(2)上述七位数中,三个偶数排在一起的有
=14
400(个).
(3)上述七位数中,3个偶数排在一起,4个奇数也排在一起的
有
(个).
(4)上述七位数中,偶数都不相邻,可先把4个奇数排好,再
将3个偶数分别插入5个空档,共有
(个).
【拓展提升】
1.解答排列、组合综合问题的一般思路和注意点
(1)一般思路:“先选后排”,也就是把符合题意的元素都选出来,再对元素或位置进行排列.
(2)注意点:①元素是否有序是区分排列与组合的基本方法,无序的问题是组合问题,有序的问题是排列问题.
②对于有多个限制条件的复杂问题,应认真分析每个限制条件,然后再考虑是分类还是分步,这是处理排列、组合的综合问题的一般方法.
2.分组、分配问题的求解策略
(1)分组问题属于“组合”问题,按组合问题求解,常见的分组问题有三种:
①完全均匀分组,每组的元素个数均相等;
②部分均匀分组,应注意不要重复,若有n组均匀,最后必须除以n!;
③完全非均匀分组,这种分组不考虑重复现象.
(2)分配问题属于“排列”问题,可以按要求逐个分配,也可以分组后再分配.
【变式训练】1.(2013·嘉兴高二检测)将红、黑、蓝、黄4个不同的小球放入3个不同的盒子,每个盒子至少放一个球,且红球和蓝球不能放在同一个盒子,则不同的放法有(
)
A.18种
B.24种
C.30种
D.36种
【解析】选C.将4个小球放入3个不同的盒子,先在4个小球中
任取2个作为1组,再将其与其他2个小球对应3个盒子,共有
种情况,若红球和蓝球放到同一个盒子,则黑、黄
球放进其余的盒子里,有
种情况,则红球和蓝球不放
到同一个盒子的放法种数为36-6=30种.
2.6本不同的书,按下列要求各有多少种不同的分法:
(1)分给甲、乙、丙三人,每人两本.
(2)分为三份,每份两本.
(3)分为三份,一份一本,一份两本,一份三本.
(4)分给甲、乙、丙三人,一人一本,一人两本,一人三本.
【解析】(1)根据分步乘法计数原理得有
种.
(2)分给甲、乙、丙三人,每人两本有
种方法,这个
过程可以分两步完成:第一步分为三份,每份两本设有x种方
法;第二步再将这三份分给甲、乙、丙三名同学有
种方法.
根据分步乘法计数原理可得:
所以
因此分为三份,每份两本一共有15种方法.
(3)这是“不均匀分组”问题,一共有
种方法.
(4)在(3)的基础上再进行全排列,所以一共有
=360种方法.
【易错误区】组合应用问题中考虑不周致误
【典例】已知集合A={1,2,3,4,5},则至少含一个偶数的集合A的子集个数为______.
【解析】直接法:
当子集中含有1个偶数时,①共有个数
(个);
当子集中含有2个偶数时:①共有
(个);
满足题意的集合A的子集个数为:16+8=24(个).
间接法:
集合A的子集共有
(个),②
不符合题意的子集有空集、分别只含有1,2,3个奇数的子
集,有
(个),故符合题意的子集个数为32
-8=24(个).
答案:24
【误区警示】
【防范措施】
1.分类不重复、不遗漏
分类时要选择一个确定的分类标准,其原则是分类不能重复,不能遗漏.如本例中对偶数个数的分类.
2.重视特殊情况在解题中的作用
解题过程中要注意分析特殊元素、特殊情况对结果的影响,并注意总结、避免因考虑问题不全面而失分.如本例中子集的特殊情况空集就容易遗漏.
【类题试解】从5名男学生、4名女学生中选3名学生组成一个
研究性学习小组,要求其中男、女学生都有,则不同的选法
有______.
【解析】根据题意,共有9名学生,从中任取3人,有
(种)取法,其中只有男生的有
(种)取法,只有女生的
有
(种)取法,则男、女学生都有的选法有84-10-4=
70(种).
答案:70种
1.楼道里有12盏灯,为了节约用电,需关掉3盏不相邻的灯,
则关灯方案有(
)
A.72种
B.84种
C.120种
D.168种
【解析】选C.需关掉3盏不相邻的灯,即将这3盏灯插入9盏亮
着的灯的空中,所以关灯方案共有
(种).
2.今有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人
承担,现从10人中选派4人承担这三项任务,不同的选派方法
有(
)
A.1
260种
B.2
025种
C.2
520种
D.5
054种
【解析】选C.先从10人中选出4个人,再在这4个人中选两
个从事甲任务,剩下的两个人从事乙、丙任务,故可得出:
(种).
3.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程
中恰有1门相同的选法有(
)
A.6种
B.12种
C.24种
D.30种
【解析】选C.所有两人各选修2门的种数是
两人所选两
门都相同和都不同的种数均为
故只恰好有1门相同的选法
有
(种).
4.如图,要用三根数据线将四台电脑A,B,C,D连接起来以
实现资源共享,则不同的连接方案的种数是(
)
A.16
B.18
C.20
D.22
【解析】选A.画一个正方形和它的两条对角线,在这6条线
段中,选3条的选法有
(种).其中4个直角三角形不是
连接方案,故不同的连接方案共有
(种).
5.某科技小组有女同学2名、男同学x名,现从中选出3名去参
加展览.若恰有1名女生入选时的不同选法有20种,则该科技
小组中男生的人数为______.
【解析】由题意得
解得x=5.
答案:5
6.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有1名女生当选.
(2)两名队长当选.
(3)至少有1名队长当选.
(4)至多有2名女生当选.
(5)既要有队长,又要有女生当选.
【解析】(1)1名女生,4名男生,故共有
(种).
(2)将两名队长作为一类,其他11人作为一类,故共有
(种).
(3)方法一:至少有1名队长含有两类:只有1名队长;2名
队长,故共有选法
(种).
方法二:采用间接法共有
(种).
(4)至多有2名女生含有三类:有2名女生;只有1名女生;
没有女生.
故选法共有
(种).
(5)分类:第1类,女队长当选:
种;第2类,女队长不
当选:
种.故选法共有
(种).
组合的综合应用
类型一
无限制条件的组合问题
【典型例题】
1.某人决定投资3种股票和4种债券,经纪人向他推荐了6种股票和5种债券,则此人不同的投资方式有______种.
2.某高中学生会由6名男生和4名女生组成.
(1)从中选4名学生参与学校卫生大检查,共有多少种不同的选法?
(2)从男生和女生中各选2名学生去“阳光敬老院”进行某项社会调查,共有多少种不同的选法?
【解题探究】
1.题1中投资需分几步?每步选法如何用组合数表示?
2.题2(2)中完成此件事需分几步走?分别是什么?
探究提示:
1.投资需分两步:第一步投资股票有
种,第二步,投资
债券有
种.
2.分两步走,第一步从6名男生中任选2名学生.第二步从4名
女生中任选2名学生.
【解析】1.需分两步:
第一步,根据经纪人的推荐在6种股票中选3种,共有
种选
法;
第二步,根据经纪人的推荐在5种债券中选4种,共有
种选
法.
根据分步乘法计数原理,此人有
种不同的投资方
式.
答案:100
2.(1)本问题相当于从10个不同的元素中,任取4个元素,所
以共有
种不同的选法.
(2)完成这件事分两步走:第一步从6名男生中任选2名学生,
共有
种不同的选法;第二步从4名女生中任选2
名学生,共有
种不同的选法.由分步乘法计数原
理得,共有15×6=90种不同的选法.
【拓展提升】求解无限制条件组合问题的步骤与关注点
1.求解步骤
2.关注点及注意点:要关注将要计的数是分类还是分步,在分类和分步时,一定要注意有无重复或遗漏.
【变式训练】(2013·成都高二检测)给一个正方体的六个面涂上四种不同颜色(红、黄、绿、蓝),要求相邻两个面涂不同的颜色,则共有涂色方法多少种(涂色后,任意翻转正方体,能使正方体各面颜色一致,我们认为是同一种涂色方法)(
)
A.6种
B.12种
C.24种
D.48种
【解析】选A.由于涂色过程中,要保证满足条件(用四种颜
色,相邻的面不同色),正方体的三对面,必然有两对同色,
一对不同色,而且三对面具有“地位对等性”,因此,只需
从四种颜色中选择2种涂在其中一对面上,剩下的两种颜色涂
在另外两对面即可.因此共有
(种)不同的涂法.
类型二
有限制条件的组合问题
【典型例题】
1.以正方体的顶点为顶点,可以确定______个四面体.
2.(2013·青岛高二检测)某医院从10名医疗专家中抽调6名奔赴灾区救灾,其中这10名医疗专家中有4名是外科专家.问:
(1)抽调的6名专家中恰有2名是外科专家的抽调方法有多少种?
(2)抽调的6名专家中至少有2名外科专家的抽调方法有多少种?
(3)抽调的6名专家中至多有2名外科专家的抽调方法有多少种?
【解题探究】
1.构成四面体的四个点需具备什么限制条件?
2.题2中“恰有2名外科专家”“至少有2名外科专家”与“至多有2名外科专家”的含义分别是什么?
探究提示:
1.构成四面体的四个点需具备不共面这一限制条件.
2.“恰有2名外科专家”指的是抽调的6名专家中有2名是外科专家,其余4名是非外科专家.
“至少有2名外科专家”指的是有可能是2名外科专家,也可能是3名或4名.
“至多有2名外科专家”指的是可能有2名外科专家,也可能1名或没有.
【解析】1.正方体8个顶点可构成
个四点组,其中共面的
四点组有正方体的6个表面的四个顶点和正方体相对棱分别所
在6个平面的四个顶点,故可以确定的四面体有
(个).
答案:58
2.(1)分步:首先从4名外科专家中任选2名,有
种选法,
再从除外科专家的6人中选取4人,有
种选法,所以共有
种抽调方法.
(2)“至少”的含义是不低于,有两种解答方法,
方法一(直接法):按选取的外科专家的人数分类:
①选2名外科专家,共有
种选法;
②选3名外科专家,共有
种选法;
③选4名外科专家,共有
种选法.
根据分类加法计数原理,共有
种抽调方法.
方法二(间接法):不考虑是否有外科专家,共有
种选法,
考虑选取1名外科专家参加,有
种选法;没有外科专家
参加,有
种选法,所以共有
种抽调方
法.
(3)“至多2名”包括“没有”“有1名”“有2名”三种情
况,分类解答.
①没有外科专家参加,有
种选法;
②有1名外科专家参加,有
种选法;
③有2名外科专家参加,有
种选法.
所以共有
种抽调方法.
【拓展提升】有限制条件的组合应用题的常见类型及求解思路
1.“含”与“不含”问题
这类问题的解题思路是将限制条件视为特殊元素和特殊位置,一般来讲,特殊要先满足,其余则“一视同仁”.若正面入手不易,则从反面入手,寻找问题的突破口,即采用间接法.解题时要注意分清“恰有”“有且仅有”“至多”“至少”“全是”“都不是”“不都是”等词语的确切含义,准确把握分类标准.
2.几何中的计数问题
在处理几何问题中的组合应用问题时,应先明确几何中的点、线、面及构型,明确平面图形和立体图形中的点、线、面之间的关系,将几何问题抽象成组合问题来解决.
【变式训练】1.在四棱锥P-ABCD中,顶点为P,从其他的顶点和各棱的中点中取3个,使它们和点P在同一平面内,不同的取法有(
)
A.40种
B.48种
C.56种
D.62种
【解析】选C.如图,
满足题设的取法可分为三类:
①在四棱锥的每个侧面上除
点P外任取3点,有
(种)不同的取法;
②在两个对角面上除点P外任取3点,共有
(种)不同
的取法;
③过点P的每一条棱上的三点和与这条棱异面的棱的中点也共
面,共有
(种)不同的取法.
故不同的取法共有40+8+8=56(种).
2.一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出3个球,共有多少种取法
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法
【解析】(1)
(种).
(2)从7个白球中任选2个,共有
(种).
(3)从7个白球中任选3个,共有
(种).
类型三
排列、组合的综合应用
【典型例题】
1.(2013·长春高二检测)某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数有(
)
A.6种
B.24种
C.180种
D.90种
2.(2013·安阳高二检测)从1到9的九个数字中取三个偶数四个奇数.试问:
(1)能组成多少个没有重复数字的七位数?
(2)上述七位数中三个偶数排在一起的有几个?
(3)(1)中的七位数中,偶数排在一起,奇数也排在一起的有几个?
(4)(1)中任意两个偶数都不相邻的七位数有几个?
【解题探究】
1.题1中的4名学生安排到两个班级是平均分组还是非平均分组 分组后还要分配吗?
2.题2(1)中组成没有重复数字的七位数,需要分几步完成?各是什么问题?
题2(2)中七位数中要求三个偶数排在一起,应如何安排?
题2(3)中的七位数应如何排?
题2(4)中的七位数应如何排?
探究提示:
1.是平均分组,且分组后需要分配.
2.组成题2(1)中的七位数,需分三步即第1步取3个偶数为组合问题,第二步取4个奇数为组合问题,第3步将取出的7个数排序,为排列问题.
题2(2)可用“捆绑法”安排.
题2(3)分别用“捆绑法”安排.
题2(4)可对偶数用插空法安排.
【解析】1.选D.先把4名学生分两组有
(种),然后
再把这两组给这6个班中的两个班有
(种),根据分步乘
法计数原理得不同的安排方案种数有3×30=90(种).
2.(1)分步完成:第一步在4个偶数中取3个,可有
种情
况;第二步在5个奇数中取4个,可有
种情况;第三步3
个偶数,4个奇数进行排列,可有
种情况,所以符合题
意的七位数有
(个).
(2)上述七位数中,三个偶数排在一起的有
=14
400(个).
(3)上述七位数中,3个偶数排在一起,4个奇数也排在一起的
有
(个).
(4)上述七位数中,偶数都不相邻,可先把4个奇数排好,再
将3个偶数分别插入5个空档,共有
(个).
【拓展提升】
1.解答排列、组合综合问题的一般思路和注意点
(1)一般思路:“先选后排”,也就是把符合题意的元素都选出来,再对元素或位置进行排列.
(2)注意点:①元素是否有序是区分排列与组合的基本方法,无序的问题是组合问题,有序的问题是排列问题.
②对于有多个限制条件的复杂问题,应认真分析每个限制条件,然后再考虑是分类还是分步,这是处理排列、组合的综合问题的一般方法.
2.分组、分配问题的求解策略
(1)分组问题属于“组合”问题,按组合问题求解,常见的分组问题有三种:
①完全均匀分组,每组的元素个数均相等;
②部分均匀分组,应注意不要重复,若有n组均匀,最后必须除以n!;
③完全非均匀分组,这种分组不考虑重复现象.
(2)分配问题属于“排列”问题,可以按要求逐个分配,也可以分组后再分配.
【变式训练】1.(2013·嘉兴高二检测)将红、黑、蓝、黄4个不同的小球放入3个不同的盒子,每个盒子至少放一个球,且红球和蓝球不能放在同一个盒子,则不同的放法有(
)
A.18种
B.24种
C.30种
D.36种
【解析】选C.将4个小球放入3个不同的盒子,先在4个小球中
任取2个作为1组,再将其与其他2个小球对应3个盒子,共有
种情况,若红球和蓝球放到同一个盒子,则黑、黄
球放进其余的盒子里,有
种情况,则红球和蓝球不放
到同一个盒子的放法种数为36-6=30种.
2.6本不同的书,按下列要求各有多少种不同的分法:
(1)分给甲、乙、丙三人,每人两本.
(2)分为三份,每份两本.
(3)分为三份,一份一本,一份两本,一份三本.
(4)分给甲、乙、丙三人,一人一本,一人两本,一人三本.
【解析】(1)根据分步乘法计数原理得有
种.
(2)分给甲、乙、丙三人,每人两本有
种方法,这个
过程可以分两步完成:第一步分为三份,每份两本设有x种方
法;第二步再将这三份分给甲、乙、丙三名同学有
种方法.
根据分步乘法计数原理可得:
所以
因此分为三份,每份两本一共有15种方法.
(3)这是“不均匀分组”问题,一共有
种方法.
(4)在(3)的基础上再进行全排列,所以一共有
=360种方法.
【易错误区】组合应用问题中考虑不周致误
【典例】已知集合A={1,2,3,4,5},则至少含一个偶数的集合A的子集个数为______.
【解析】直接法:
当子集中含有1个偶数时,①共有个数
(个);
当子集中含有2个偶数时:①共有
(个);
满足题意的集合A的子集个数为:16+8=24(个).
间接法:
集合A的子集共有
(个),②
不符合题意的子集有空集、分别只含有1,2,3个奇数的子
集,有
(个),故符合题意的子集个数为32
-8=24(个).
答案:24
【误区警示】
【防范措施】
1.分类不重复、不遗漏
分类时要选择一个确定的分类标准,其原则是分类不能重复,不能遗漏.如本例中对偶数个数的分类.
2.重视特殊情况在解题中的作用
解题过程中要注意分析特殊元素、特殊情况对结果的影响,并注意总结、避免因考虑问题不全面而失分.如本例中子集的特殊情况空集就容易遗漏.
【类题试解】从5名男学生、4名女学生中选3名学生组成一个
研究性学习小组,要求其中男、女学生都有,则不同的选法
有______.
【解析】根据题意,共有9名学生,从中任取3人,有
(种)取法,其中只有男生的有
(种)取法,只有女生的
有
(种)取法,则男、女学生都有的选法有84-10-4=
70(种).
答案:70种
1.楼道里有12盏灯,为了节约用电,需关掉3盏不相邻的灯,
则关灯方案有(
)
A.72种
B.84种
C.120种
D.168种
【解析】选C.需关掉3盏不相邻的灯,即将这3盏灯插入9盏亮
着的灯的空中,所以关灯方案共有
(种).
2.今有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人
承担,现从10人中选派4人承担这三项任务,不同的选派方法
有(
)
A.1
260种
B.2
025种
C.2
520种
D.5
054种
【解析】选C.先从10人中选出4个人,再在这4个人中选两
个从事甲任务,剩下的两个人从事乙、丙任务,故可得出:
(种).
3.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程
中恰有1门相同的选法有(
)
A.6种
B.12种
C.24种
D.30种
【解析】选C.所有两人各选修2门的种数是
两人所选两
门都相同和都不同的种数均为
故只恰好有1门相同的选法
有
(种).
4.如图,要用三根数据线将四台电脑A,B,C,D连接起来以
实现资源共享,则不同的连接方案的种数是(
)
A.16
B.18
C.20
D.22
【解析】选A.画一个正方形和它的两条对角线,在这6条线
段中,选3条的选法有
(种).其中4个直角三角形不是
连接方案,故不同的连接方案共有
(种).
5.某科技小组有女同学2名、男同学x名,现从中选出3名去参
加展览.若恰有1名女生入选时的不同选法有20种,则该科技
小组中男生的人数为______.
【解析】由题意得
解得x=5.
答案:5
6.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有1名女生当选.
(2)两名队长当选.
(3)至少有1名队长当选.
(4)至多有2名女生当选.
(5)既要有队长,又要有女生当选.
【解析】(1)1名女生,4名男生,故共有
(种).
(2)将两名队长作为一类,其他11人作为一类,故共有
(种).
(3)方法一:至少有1名队长含有两类:只有1名队长;2名
队长,故共有选法
(种).
方法二:采用间接法共有
(种).
(4)至多有2名女生含有三类:有2名女生;只有1名女生;
没有女生.
故选法共有
(种).
(5)分类:第1类,女队长当选:
种;第2类,女队长不
当选:
种.故选法共有
(种).
