沪教版(上海)数学高三上册-16.1计数原理I ——乘法原理_(课件)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.1计数原理I ——乘法原理_(课件) |  | |
| 格式 | ppt | ||
| 文件大小 | 232.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 22:42:22 | ||
图片预览



文档简介
(共9张PPT)
计数原理I----乘法原理
教学目标:
1.
通过实例分析,学习和掌握计数原理I----乘法原理
2.
掌握解决计数问题的最基本方法:“枚举法”,会用:“枚举法”以及乘法原理进行计数
3.
学习与感受数学模型的概括性、典型性、普遍性之美
一.计数问题的引入
问题1.某绿地如图,某人由A入口进入绿地,顺着道路走到B出口,有几种不同的行走路线
A
B
C
先由A C:2条路径;
再由C B:3条路径.
问题2.多项式(a1+a2+…+a10)(b1+b2+…+b15)展开后出现多少个单项
答:从A到B有2×3=6种不同的行走路线
答:展开后有10×15=150个单项
二.计数原理I----分步乘法原理
“分步乘法”原理:如果完成一件事需要n个步骤,
做第1步有m1种不同方法,做第2步有m2种不同方法,
…
,做第n步有mn种不同方法,那么完成这件事共有:
N=m1×m2×…×mn种不同办法.
“分步”理解:①仅完成第k步工作时,整件事不能完成;
②当且仅当n个步骤工作都经历时,整件事算完成.
第1步
m1种
第2步
m2种
第n步
mn种
……
……
“分步乘法”原理的图示模型:完成从P到Q工作
P
Q
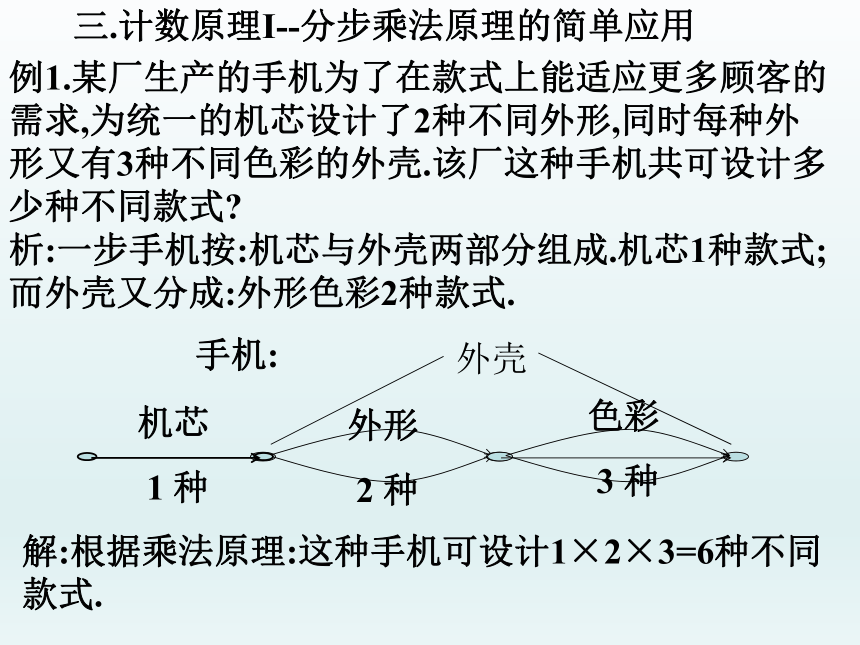
三.计数原理I--分步乘法原理的简单应用
例1.某厂生产的手机为了在款式上能适应更多顾客的需求,为统一的机芯设计了2种不同外形,同时每种外形又有3种不同色彩的外壳.该厂这种手机共可设计多少种不同款式
析:一步手机按:机芯与外壳两部分组成.机芯1种款式;而外壳又分成:外形色彩2种款式.
外形
2
种
手机:
机芯
1
种
色彩
3
种
外壳
解:根据乘法原理:这种手机可设计1×2×3=6种不同款式.
例2.如图的程序模块中,一条执行路径就是一条遵循着线段的箭头方向、从开始到结束的路径.要测试该程序模块的所有执行路径,共要测试多少次
模块开始
模块结束
子模块2
子模块1
解:根据乘法原理:共要测试3×7=21次.
例3.
630的不同正约数有多少个
解:
630=2×32×5×7
630的正约数=
2a×3b×5c×7d
形式
a可取0,1,b可取0,1,2,c可取0,1,d可取0,1
a、
b
、
c
、
d的不同取法,可得到630的不同正约数
∴630的不同正约数有:2×3×2×2=24
1.某服装厂为学校设计了4种式样的上衣,3种式样的裤子,若取其中的一件上衣和一条裤子配成校服,则可以有多少种不同式样的校服
2.某农场要在4种不同类型的土地上,试验4种(设为A、B、C、D)不同品种的小麦.共有多少种不同的试验方案
解法1:(土地选种子)第1步,第1块地从4个品种中选1种小麦进行种植试验,有4种方案;
第2步,第2块地从余下3个品种中选1种小麦进行种植试验,有3种方案;
第3步,第3块地从余下2个品种中选1种小麦进行种植试验,有2种方案;
第4步,第4块地从余下1个品种中选1种小麦进行种植试验,只有1种方案.
答:共有4×3×2×1=24种不同的试验方案
3.在一种两位的编码方式中,规定第一位用阿拉伯数字0~9,第二位用某小写26个英文字母.这种编码方式共产生多少种不同的编码
4.如果一个正整数n可分解成
,其中
均为互不相同的素数,
均为正整数,那么n的不同正约数共有多少个
p1、p2、p3
、 、
n=p1
·
p2
·
p3
解:n的正约数中,其中的p1指数 可取0,1,2,…, 共 +1个、
∴n的不同正约数共有
个.
( +1)
( +1)(
+1)
p2的指数 可取0,1,2,…, 共 +1个、
p3的指数 可取0,1,2,…, 共 +1个
5.注册一个网络免费邮箱
,其中设定个人的密码可以用0~9的数字,也可以用26个大(或小)写英文字母组成的一个6~32个字符
(不能空格)作为个人邮箱的密码.
假设某人想设定一个6位密码,且开头用一个英文大写字母,后五位都用数字,则共有多少种不同设定密码方法
解:6位密码可用6个空格代替,
第1个空格26种设定方案
26
10
第2个空格0~9这10个数字之一,有10种设定方案
10
第3个空格0~9这10个数字之一,有10种设定方案
10
第4个空格0~9这10个数字之一,有10种设定方案
10
第5个空格0~9这10个数字之一,有10种设定方案
10
第6个空格0~9这10个数字之一,有10种设定方案
∴共有26×106种不同设定密码方法.
计数原理I----乘法原理
教学目标:
1.
通过实例分析,学习和掌握计数原理I----乘法原理
2.
掌握解决计数问题的最基本方法:“枚举法”,会用:“枚举法”以及乘法原理进行计数
3.
学习与感受数学模型的概括性、典型性、普遍性之美
一.计数问题的引入
问题1.某绿地如图,某人由A入口进入绿地,顺着道路走到B出口,有几种不同的行走路线
A
B
C
先由A C:2条路径;
再由C B:3条路径.
问题2.多项式(a1+a2+…+a10)(b1+b2+…+b15)展开后出现多少个单项
答:从A到B有2×3=6种不同的行走路线
答:展开后有10×15=150个单项
二.计数原理I----分步乘法原理
“分步乘法”原理:如果完成一件事需要n个步骤,
做第1步有m1种不同方法,做第2步有m2种不同方法,
…
,做第n步有mn种不同方法,那么完成这件事共有:
N=m1×m2×…×mn种不同办法.
“分步”理解:①仅完成第k步工作时,整件事不能完成;
②当且仅当n个步骤工作都经历时,整件事算完成.
第1步
m1种
第2步
m2种
第n步
mn种
……
……
“分步乘法”原理的图示模型:完成从P到Q工作
P
Q
三.计数原理I--分步乘法原理的简单应用
例1.某厂生产的手机为了在款式上能适应更多顾客的需求,为统一的机芯设计了2种不同外形,同时每种外形又有3种不同色彩的外壳.该厂这种手机共可设计多少种不同款式
析:一步手机按:机芯与外壳两部分组成.机芯1种款式;而外壳又分成:外形色彩2种款式.
外形
2
种
手机:
机芯
1
种
色彩
3
种
外壳
解:根据乘法原理:这种手机可设计1×2×3=6种不同款式.
例2.如图的程序模块中,一条执行路径就是一条遵循着线段的箭头方向、从开始到结束的路径.要测试该程序模块的所有执行路径,共要测试多少次
模块开始
模块结束
子模块2
子模块1
解:根据乘法原理:共要测试3×7=21次.
例3.
630的不同正约数有多少个
解:
630=2×32×5×7
630的正约数=
2a×3b×5c×7d
形式
a可取0,1,b可取0,1,2,c可取0,1,d可取0,1
a、
b
、
c
、
d的不同取法,可得到630的不同正约数
∴630的不同正约数有:2×3×2×2=24
1.某服装厂为学校设计了4种式样的上衣,3种式样的裤子,若取其中的一件上衣和一条裤子配成校服,则可以有多少种不同式样的校服
2.某农场要在4种不同类型的土地上,试验4种(设为A、B、C、D)不同品种的小麦.共有多少种不同的试验方案
解法1:(土地选种子)第1步,第1块地从4个品种中选1种小麦进行种植试验,有4种方案;
第2步,第2块地从余下3个品种中选1种小麦进行种植试验,有3种方案;
第3步,第3块地从余下2个品种中选1种小麦进行种植试验,有2种方案;
第4步,第4块地从余下1个品种中选1种小麦进行种植试验,只有1种方案.
答:共有4×3×2×1=24种不同的试验方案
3.在一种两位的编码方式中,规定第一位用阿拉伯数字0~9,第二位用某小写26个英文字母.这种编码方式共产生多少种不同的编码
4.如果一个正整数n可分解成
,其中
均为互不相同的素数,
均为正整数,那么n的不同正约数共有多少个
p1、p2、p3
、 、
n=p1
·
p2
·
p3
解:n的正约数中,其中的p1指数 可取0,1,2,…, 共 +1个、
∴n的不同正约数共有
个.
( +1)
( +1)(
+1)
p2的指数 可取0,1,2,…, 共 +1个、
p3的指数 可取0,1,2,…, 共 +1个
5.注册一个网络免费邮箱
,其中设定个人的密码可以用0~9的数字,也可以用26个大(或小)写英文字母组成的一个6~32个字符
(不能空格)作为个人邮箱的密码.
假设某人想设定一个6位密码,且开头用一个英文大写字母,后五位都用数字,则共有多少种不同设定密码方法
解:6位密码可用6个空格代替,
第1个空格26种设定方案
26
10
第2个空格0~9这10个数字之一,有10种设定方案
10
第3个空格0~9这10个数字之一,有10种设定方案
10
第4个空格0~9这10个数字之一,有10种设定方案
10
第5个空格0~9这10个数字之一,有10种设定方案
10
第6个空格0~9这10个数字之一,有10种设定方案
∴共有26×106种不同设定密码方法.
