沪教版(上海)数学高三上册-14.2 空间直线与直线的位置关系 (课件)(共19张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-14.2 空间直线与直线的位置关系 (课件)(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 644.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:34:22 | ||
图片预览





文档简介
(共19张PPT)
复习引入:
1、同一平面内不重合两条直线有几种位置关系?
2、在同一平面内,平行于同一条直线的两条直线有什么位置关系?
(1)
相交:有且仅有一个公共点。
(2)
平行:在同一平面内没有公共点。
互相平行
提出问题:如果空间中的两条直线都与第三条直线平行,那么这两条直线之间的位置关系如何呢?
复习
公理4:平行于同一直线的两条直线互相平行。
注:公理4实质上是说平面上平行直线的传递性可以推广到空间。
公理4作用:判断空间两条直线平行的依据。
a∥b
c∥b
a∥c
符号表示:设空间中的三条直线分别为a,
b,
c,若
想一想:
空间中,如果两条直线都与第三条直线垂直,是否也有类似的规律
例题讲解
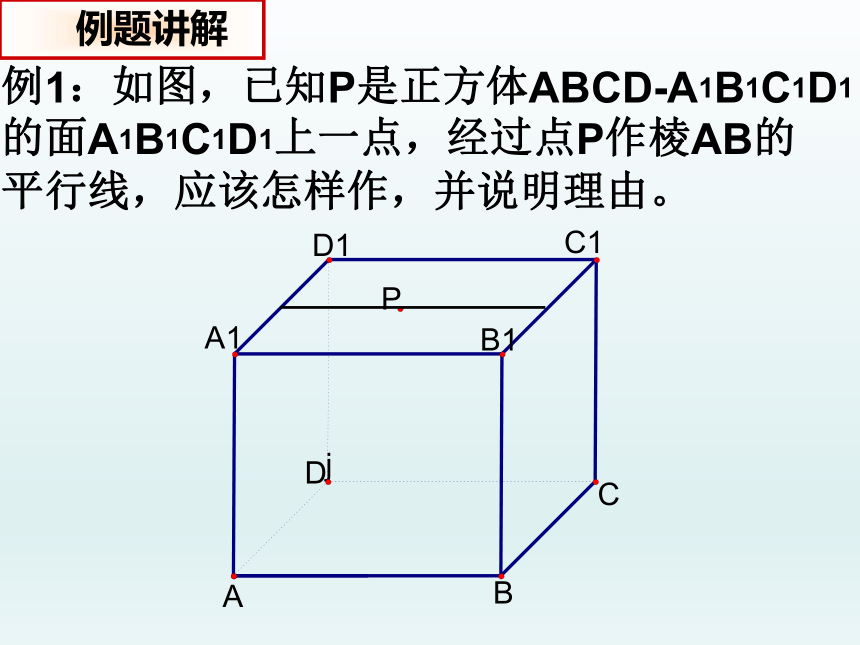
例1:如图,已知P是正方体ABCD-A1B1C1D1
的面A1B1C1D1上一点,经过点P作棱AB的
平行线,应该怎样作,并说明理由。
例题讲解
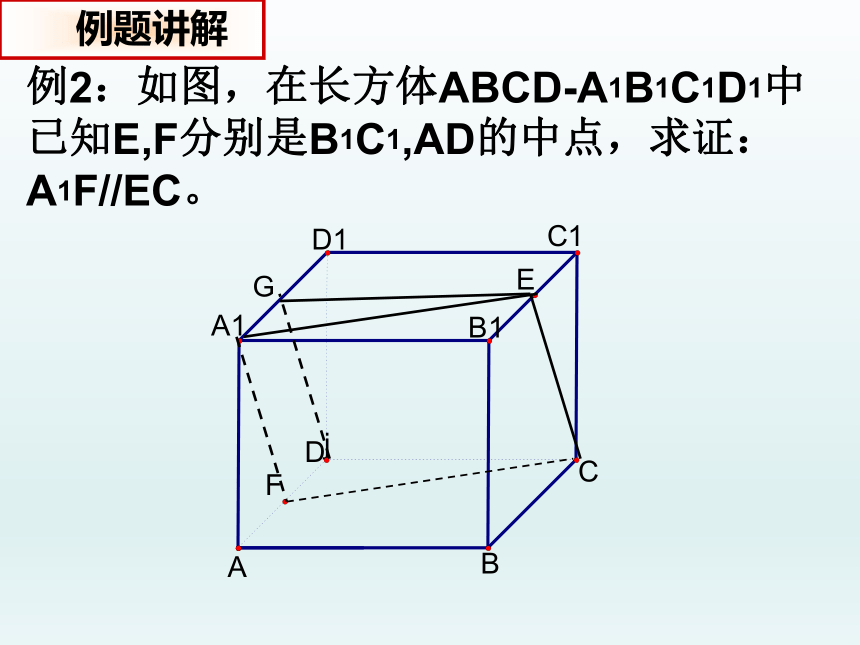
例2:如图,在长方体ABCD-A1B1C1D1中
已知E,F分别是B1C1,AD的中点,求证:
A1F//EC。
G
提出问题:
在平面上,我们有等角定理成立,即“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”。在空间中,这个结论是否仍然成立呢
复习
定理1
如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
定理1的推论:
如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
观察
定义
归纳:空间不重合的两直线位置关系
异面直线所成角
思考题:已知正四面体ABCD中,E、F分别是BC、
AD的中点,求
(1)直线EF、AC所成角的大小;
(2)直线AE、CF所成角的大小。
C
B
D
A
E
F
M
复习引入:
1、同一平面内不重合两条直线有几种位置关系?
2、在同一平面内,平行于同一条直线的两条直线有什么位置关系?
(1)
相交:有且仅有一个公共点。
(2)
平行:在同一平面内没有公共点。
互相平行
提出问题:如果空间中的两条直线都与第三条直线平行,那么这两条直线之间的位置关系如何呢?
复习
公理4:平行于同一直线的两条直线互相平行。
注:公理4实质上是说平面上平行直线的传递性可以推广到空间。
公理4作用:判断空间两条直线平行的依据。
a∥b
c∥b
a∥c
符号表示:设空间中的三条直线分别为a,
b,
c,若
想一想:
空间中,如果两条直线都与第三条直线垂直,是否也有类似的规律
例题讲解
例1:如图,已知P是正方体ABCD-A1B1C1D1
的面A1B1C1D1上一点,经过点P作棱AB的
平行线,应该怎样作,并说明理由。
例题讲解
例2:如图,在长方体ABCD-A1B1C1D1中
已知E,F分别是B1C1,AD的中点,求证:
A1F//EC。
G
提出问题:
在平面上,我们有等角定理成立,即“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”。在空间中,这个结论是否仍然成立呢
复习
定理1
如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
定理1的推论:
如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
观察
定义
归纳:空间不重合的两直线位置关系
异面直线所成角
思考题:已知正四面体ABCD中,E、F分别是BC、
AD的中点,求
(1)直线EF、AC所成角的大小;
(2)直线AE、CF所成角的大小。
C
B
D
A
E
F
M
