沪教版(上海)数学高三下册-18.5 概率统计实验 (教案)
文档属性
| 名称 | 沪教版(上海)数学高三下册-18.5 概率统计实验 (教案) |
|
|
| 格式 | doc | ||
| 文件大小 | 76.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览


文档简介
概率统计实验
【教学目标】
1.理解随机数的基本概念;
2.会用Scilab语言求一维和二维随机数;
3.掌握随机投点法在实际问题中的基本应用。
【教学重难点】
重点:随机投点法的应用。
难点:几何概率、Scilab语言。
【教学准备】
多媒体设备、网络。
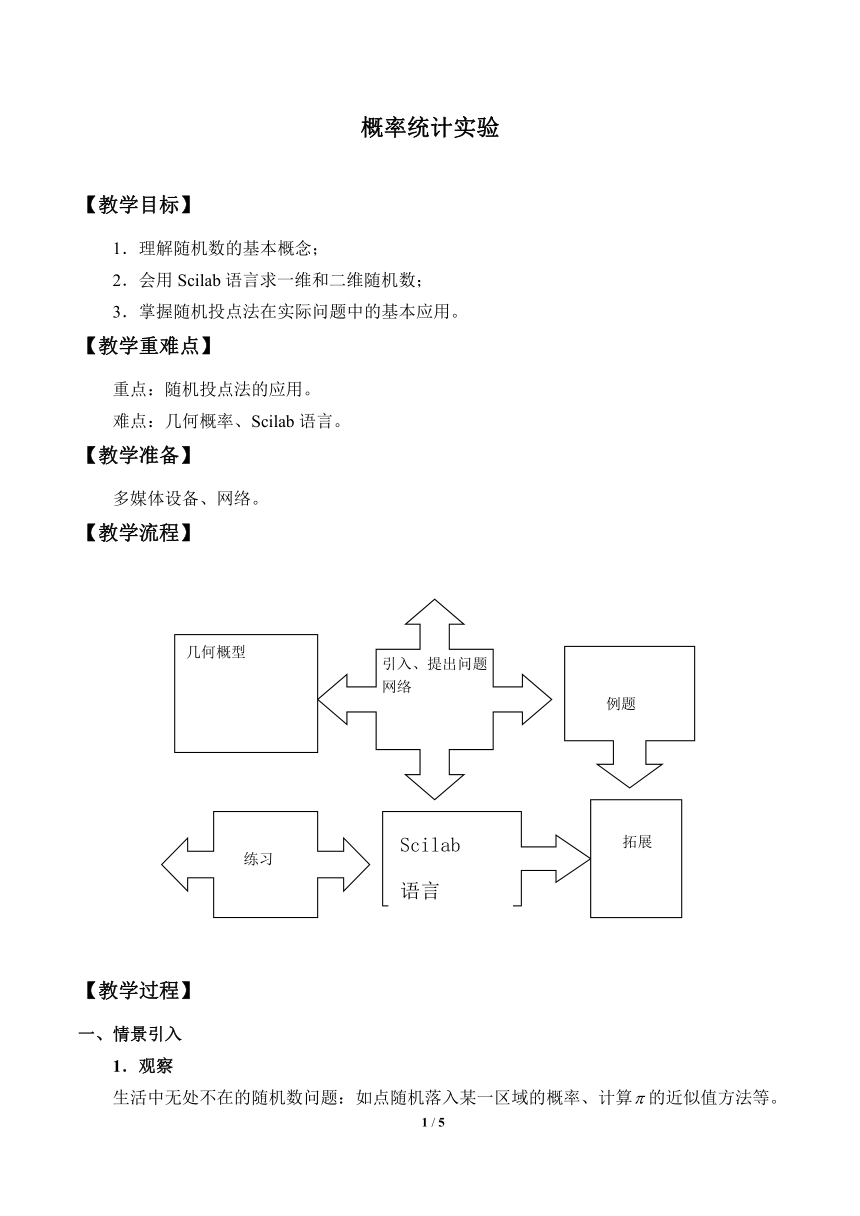
【教学流程】
【教学过程】
一、情景引入
1.观察
生活中无处不在的随机数问题:如点随机落入某一区域的概率、计算的近似值方法等。
2.思考
这容易引起我们思考用什么工具来完成上述问题,下面我们就这个问题展开讨论。
3.讨论
(1)本节中提到了几个概念?(分组讨论)
(2)对概率的基本概念是否熟悉?
二、学习新课
1.概念辨析
一维随机数:等可能地落在内的点所对应的实数叫做一维随机数。
二维随机数:直角坐标系的平面上边长为1,其一个顶点在坐标原点,两边分别在轴上的正方形内均匀分布点的坐标是二维随机数。
伪随机数:利用计算机程序产生的一维随机数和二维随机数称为伪随机数。简称随机数。
本课内容就是利用随机数在计算机上进行一些有趣的实验。
2.例题分析
例1:利用随机投点法求得近似值。
解:如图:D是正方形OABC的内接圆。正方形的边长为1,在正方形内随机投N个点,由n个点落在D内。
由几何概率:,
由此得:。
只要统计随机投点P(x,y)落在D中的点的个数n,即可求得π的近似值,只要判断是否成立即可。
统计投点落在D内的个数的计算机程序框图如下:
Scilab语言程序:
注:(1)rand(1,2)是1行2列随机数组,其中数的值均在0与1之间。
(2)s是1行2列的数组(行向量)。
(3)norm(s)表示向量的模。
对于N=1000,10000,100000,三种实验结果列表如下:
投点数N
第一次试验结果
第二次试验结果
第三次试验结果
三次试验结果平均值
1000
3.109
3.136
3.212
3.152
10000
3.1580
3.1228
3.1696
3.1501
100000
3.1378
3.1432
3.1438
3.1416
注:
(1)表中计算机显示的结果当N=1000时取3位小数,当N=10000以上时,取4位小数。
(2)关于几何概率的有关知识:
例2:用随机投点法求抛物线与x轴组成的封闭图形的面积。
解:在正方形中随机投N个点,如果其中有n个点落在所求得封闭图形(阴影部分)内,考虑到投点是等可能的,所以
,
正方形ABCD的面积是16,所以
为了得到区间上的随机数,我们把计算机中的随机数取出后进行下列计算:
(x,y)是均匀分布在正方形ABCD内的随机数。
计算投点落在阴影部分内的个数的Scilab语言程序:
得到阴影部分面积(抛物线与x轴组成的封闭图形的面积):
投点数N
第一次试验结果
第二次试验结果
第三次试验结果
三次试验结果平均值
1000
10.768
10.784
10.688
10.747
10000
10.6636
10.6288
10.5824
10.6249
100000
10.6730
10.6558
10.6339
10.6542
3.问题拓展
本节课中涉及到几何概型、Scilab语言程序
。请同学们可参阅提供的网页,自行提出问题,进行讨论
。
三、巩固练习
已知图中四点的坐标:A(-1,0)、B(1,0)、C(0,1)、D(0,),利用随机投点法求下图中月牙形(阴影部分)的面积。月牙形的边是圆心为O的圆弧,椭圆弧ADB是长轴为AB,短半轴为OD的椭圆的一部分。
四、课堂小结
本节我们在理解几何概率和随机数的前提下进行了一些有趣的实验,直到利用Scilab语言进行的概率统计试验的重要性,基本了解随机投点法在实际问题中的基本应用。
引入、提出问题
网络
几何概型
例题
拓展
Scilab
语言
练习
A
O
B
x
D
C
y
1
/
1
【教学目标】
1.理解随机数的基本概念;
2.会用Scilab语言求一维和二维随机数;
3.掌握随机投点法在实际问题中的基本应用。
【教学重难点】
重点:随机投点法的应用。
难点:几何概率、Scilab语言。
【教学准备】
多媒体设备、网络。
【教学流程】
【教学过程】
一、情景引入
1.观察
生活中无处不在的随机数问题:如点随机落入某一区域的概率、计算的近似值方法等。
2.思考
这容易引起我们思考用什么工具来完成上述问题,下面我们就这个问题展开讨论。
3.讨论
(1)本节中提到了几个概念?(分组讨论)
(2)对概率的基本概念是否熟悉?
二、学习新课
1.概念辨析
一维随机数:等可能地落在内的点所对应的实数叫做一维随机数。
二维随机数:直角坐标系的平面上边长为1,其一个顶点在坐标原点,两边分别在轴上的正方形内均匀分布点的坐标是二维随机数。
伪随机数:利用计算机程序产生的一维随机数和二维随机数称为伪随机数。简称随机数。
本课内容就是利用随机数在计算机上进行一些有趣的实验。
2.例题分析
例1:利用随机投点法求得近似值。
解:如图:D是正方形OABC的内接圆。正方形的边长为1,在正方形内随机投N个点,由n个点落在D内。
由几何概率:,
由此得:。
只要统计随机投点P(x,y)落在D中的点的个数n,即可求得π的近似值,只要判断是否成立即可。
统计投点落在D内的个数的计算机程序框图如下:
Scilab语言程序:
注:(1)rand(1,2)是1行2列随机数组,其中数的值均在0与1之间。
(2)s是1行2列的数组(行向量)。
(3)norm(s)表示向量的模。
对于N=1000,10000,100000,三种实验结果列表如下:
投点数N
第一次试验结果
第二次试验结果
第三次试验结果
三次试验结果平均值
1000
3.109
3.136
3.212
3.152
10000
3.1580
3.1228
3.1696
3.1501
100000
3.1378
3.1432
3.1438
3.1416
注:
(1)表中计算机显示的结果当N=1000时取3位小数,当N=10000以上时,取4位小数。
(2)关于几何概率的有关知识:
例2:用随机投点法求抛物线与x轴组成的封闭图形的面积。
解:在正方形中随机投N个点,如果其中有n个点落在所求得封闭图形(阴影部分)内,考虑到投点是等可能的,所以
,
正方形ABCD的面积是16,所以
为了得到区间上的随机数,我们把计算机中的随机数取出后进行下列计算:
(x,y)是均匀分布在正方形ABCD内的随机数。
计算投点落在阴影部分内的个数的Scilab语言程序:
得到阴影部分面积(抛物线与x轴组成的封闭图形的面积):
投点数N
第一次试验结果
第二次试验结果
第三次试验结果
三次试验结果平均值
1000
10.768
10.784
10.688
10.747
10000
10.6636
10.6288
10.5824
10.6249
100000
10.6730
10.6558
10.6339
10.6542
3.问题拓展
本节课中涉及到几何概型、Scilab语言程序
。请同学们可参阅提供的网页,自行提出问题,进行讨论
。
三、巩固练习
已知图中四点的坐标:A(-1,0)、B(1,0)、C(0,1)、D(0,),利用随机投点法求下图中月牙形(阴影部分)的面积。月牙形的边是圆心为O的圆弧,椭圆弧ADB是长轴为AB,短半轴为OD的椭圆的一部分。
四、课堂小结
本节我们在理解几何概率和随机数的前提下进行了一些有趣的实验,直到利用Scilab语言进行的概率统计试验的重要性,基本了解随机投点法在实际问题中的基本应用。
引入、提出问题
网络
几何概型
例题
拓展
Scilab
语言
练习
A
O
B
x
D
C
y
1
/
1
