2021-2022学年度人教版数学八年级上册 11.3.2多边形的内角和学案(无答案)
文档属性
| 名称 | 2021-2022学年度人教版数学八年级上册 11.3.2多边形的内角和学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 222.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 10:00:24 | ||
图片预览

文档简介
11.3.2多边形的内角和
[学习目标]
理解,识记并会正确运用多边形的内角和、外角和公式.
[学习过程]
一、板书课题,揭示目标
导入语:同学们,我们已经知道三角形的内角和是180°,那么四边形,五边形,六边形……的内角和是多少度呢?今天我们来学习11.3.2多边形的内角和(师板书).本节课的学习目标是什么呢?请看投影
二、
出示学习目标
过渡语:怎样才能当堂达到学习目标呢?请同学们按照自学指导认真自学.
三、出示自学指导
自学指导
认真看课本(P21—P22例1结束).要求:
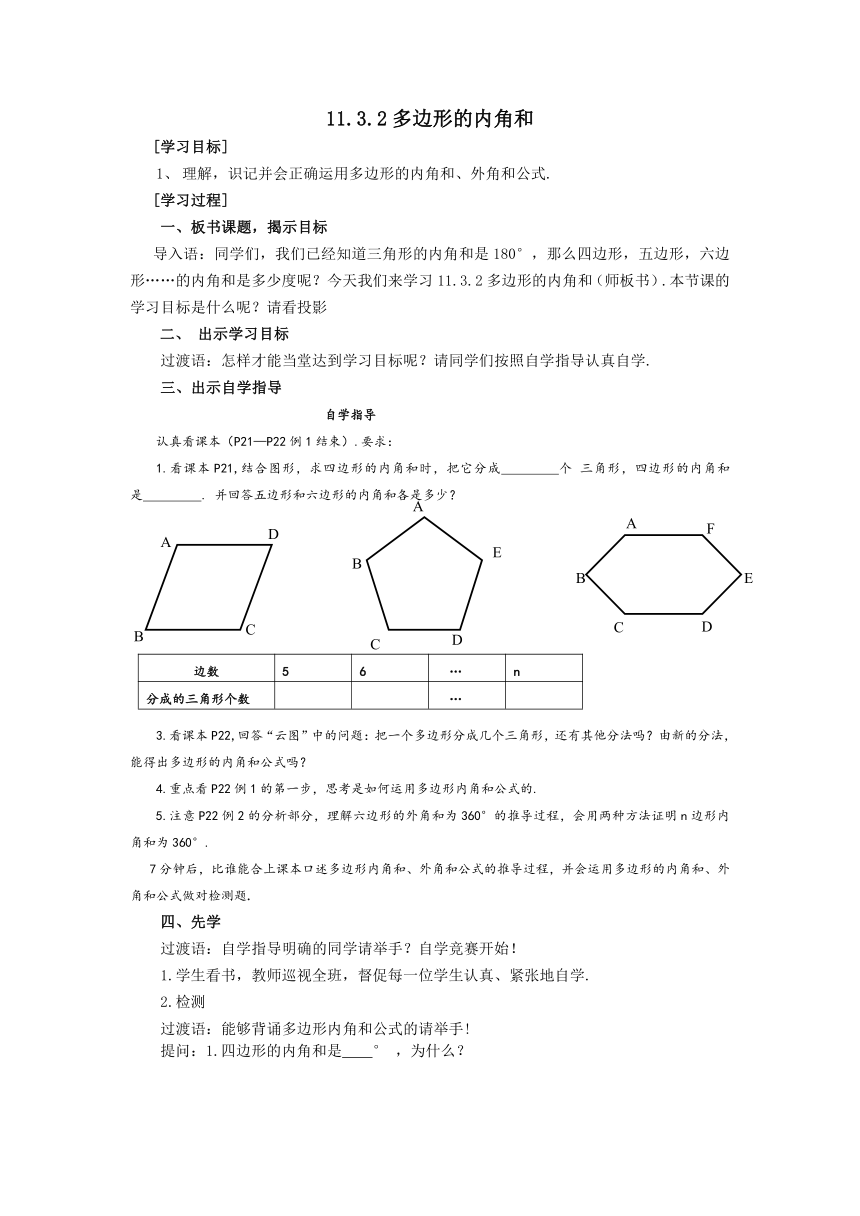
1.看课本P21,结合图形,求四边形的内角和时,把它分成
个
三角形,四边形的内角和是
.
并回答五边形和六边形的内角和各是多少?
边数
5
6
…
n
分成的三角形个数
…
3.看课本P22,回答“云图”中的问题:把一个多边形分成几个三角形,还有其他分法吗?由新的分法,能得出多边形的内角和公式吗?
4.重点看P22例1的第一步,思考是如何运用多边形内角和公式的.
5.注意P22例2的分析部分,理解六边形的外角和为360°的推导过程,会用两种方法证明n边形内角和为360°.
7分钟后,比谁能合上课本口述多边形内角和、外角和公式的推导过程,并会运用多边形的内角和、外角和公式做对检测题.
四、先学
过渡语:自学指导明确的同学请举手?自学竞赛开始!
1.学生看书,教师巡视全班,督促每一位学生认真、紧张地自学.
2.检测
过渡语:能够背诵多边形内角和公式的请举手!
提问:1.四边形的内角和是
°
,为什么?
生:分割成2个三角形,180°×2=360°.
2.五边形的内角和
°
,为什么?
生:分割成3个三角形,180°×3=540°.
3.
n边形的内角和
°
,为什么?
生:分割成(n-2)个三角形,180°×(n-2).
(3)若一个多边形的内角和是540°,则该多边形的边数是
.
4.
六边形外角和是
°
,为什么?
生:即六个平角减去六边形内角和等于六边形外角和.即6ⅹ180°-180°ⅹ(6-2)=180°ⅹ2=360°
5.
n边形外角和等于多少度?
类比推理并小结:n边形外角和等于n个平角减去n边形内角和,与边数无关.即nⅹ180°-180°ⅹ(n-2)=180°ⅹ2=360°.
另一种方法:小明家有一张六边形的地毯,小明绕各顶点走了一圈,回到起点A,并面对他出发时的方向,他的身体旋转了多少度?
一个多边形的每一个外角都是60°,那么这个多边形是(
)
A.正方形
B.正三角形
C.六边形
D.正六边形
过渡语:同学们,下面比一比看谁能正确运用多边形内角和公式做对检测题.
自学检测题
1.直接运用多边形内角和公式填表
多边形的边数
3
4
5
6
8
12
内角和
一个多边形的各个内角都等于120°,它是几边形?(设未知数,列方程)
拓展:如图,某人从点A出发,前进8m后向右转60°,再前进8m后又右转60°,按照这样的方式一直走下去,当他第一次回到出发点A时,共走了多少
m?
要求:6分钟内独立完成.
五、后教
(一)纠错
过渡语:同学们,检测题做完的请举手?好,请交换练习纸,对照答案互评,比谁全对.
1.白板逐题出示答案,学生交换试卷互评.
2.了解学情:全对的同学请举手,书写工整的请举手,好!
3.(1)若未全对的人数少,则收齐未全对的试卷,白板一类一类地出示错题(同时出示同一题的几种错).先让做错的学生根据刚学的新知识,判定自己“哪一步错”、“为什么错”;再让做对的学生帮助补充、更正,必要时让冒尖生代替老师点拨.如果学生说得对的,教师只给肯定,不必重复讲;如果所有学生都说不对的或说不全的,教师就该讲,而且要讲好,一定要让每一位学生真正解决疑难问题,既能理解、懂得“为什么”,又能灵活运用.
(2)若未全对的人数多,则不收未全对的试卷,改为教师逐项提问,让做错的学生举手说出“哪里错”,大家讨论“为什么错”,老师作必要的补充、点拨.
4.教师把学生做错的题分类放在展示台上,白板出示,集体纠错,学生说不完整的,教师补充.
预计出现的错误:
1.写几边形时,数字没有写成汉字;
2.计算错误;
(二)拓展
过渡语:老师还想考一考大家是否真的掌握了
拓展题:.若正n边形的一个外角不大于40°,则它的边数是(
)
A.
n
=
8
B.
n
=
9
C.
n
>9且n为整数
D.
n≥9且n为整数
(三)学生默读课本,自背、互背,达到堂清.
六、课堂作业
过渡语:同学们,运用新知识做作业时,要避免检测时出现的错误.
当堂训练题
1.过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的内角和是(
)
A.360°
B.720°
C.1800°
D.1440°
2.
一个多边形的内角和是1620°,则这个多边形是
边形.
3.周长为72
且内角和为1080°的正n边形的边长为____.
4.如图,在四边形ABCD中,∠A=∠C,∠B=∠D,AB与CD有怎样的位置关系?为什么?BC与AD呢?
5.如图,五边形ABCDE的内角都相等,且∠1
=
∠2,∠3=∠4,求x的值.
拓展题:
如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=
70 ,则∠AED的度数是
.
七、教学反思
[学习目标]
理解,识记并会正确运用多边形的内角和、外角和公式.
[学习过程]
一、板书课题,揭示目标
导入语:同学们,我们已经知道三角形的内角和是180°,那么四边形,五边形,六边形……的内角和是多少度呢?今天我们来学习11.3.2多边形的内角和(师板书).本节课的学习目标是什么呢?请看投影
二、
出示学习目标
过渡语:怎样才能当堂达到学习目标呢?请同学们按照自学指导认真自学.
三、出示自学指导
自学指导
认真看课本(P21—P22例1结束).要求:
1.看课本P21,结合图形,求四边形的内角和时,把它分成
个
三角形,四边形的内角和是
.
并回答五边形和六边形的内角和各是多少?
边数
5
6
…
n
分成的三角形个数
…
3.看课本P22,回答“云图”中的问题:把一个多边形分成几个三角形,还有其他分法吗?由新的分法,能得出多边形的内角和公式吗?
4.重点看P22例1的第一步,思考是如何运用多边形内角和公式的.
5.注意P22例2的分析部分,理解六边形的外角和为360°的推导过程,会用两种方法证明n边形内角和为360°.
7分钟后,比谁能合上课本口述多边形内角和、外角和公式的推导过程,并会运用多边形的内角和、外角和公式做对检测题.
四、先学
过渡语:自学指导明确的同学请举手?自学竞赛开始!
1.学生看书,教师巡视全班,督促每一位学生认真、紧张地自学.
2.检测
过渡语:能够背诵多边形内角和公式的请举手!
提问:1.四边形的内角和是
°
,为什么?
生:分割成2个三角形,180°×2=360°.
2.五边形的内角和
°
,为什么?
生:分割成3个三角形,180°×3=540°.
3.
n边形的内角和
°
,为什么?
生:分割成(n-2)个三角形,180°×(n-2).
(3)若一个多边形的内角和是540°,则该多边形的边数是
.
4.
六边形外角和是
°
,为什么?
生:即六个平角减去六边形内角和等于六边形外角和.即6ⅹ180°-180°ⅹ(6-2)=180°ⅹ2=360°
5.
n边形外角和等于多少度?
类比推理并小结:n边形外角和等于n个平角减去n边形内角和,与边数无关.即nⅹ180°-180°ⅹ(n-2)=180°ⅹ2=360°.
另一种方法:小明家有一张六边形的地毯,小明绕各顶点走了一圈,回到起点A,并面对他出发时的方向,他的身体旋转了多少度?
一个多边形的每一个外角都是60°,那么这个多边形是(
)
A.正方形
B.正三角形
C.六边形
D.正六边形
过渡语:同学们,下面比一比看谁能正确运用多边形内角和公式做对检测题.
自学检测题
1.直接运用多边形内角和公式填表
多边形的边数
3
4
5
6
8
12
内角和
一个多边形的各个内角都等于120°,它是几边形?(设未知数,列方程)
拓展:如图,某人从点A出发,前进8m后向右转60°,再前进8m后又右转60°,按照这样的方式一直走下去,当他第一次回到出发点A时,共走了多少
m?
要求:6分钟内独立完成.
五、后教
(一)纠错
过渡语:同学们,检测题做完的请举手?好,请交换练习纸,对照答案互评,比谁全对.
1.白板逐题出示答案,学生交换试卷互评.
2.了解学情:全对的同学请举手,书写工整的请举手,好!
3.(1)若未全对的人数少,则收齐未全对的试卷,白板一类一类地出示错题(同时出示同一题的几种错).先让做错的学生根据刚学的新知识,判定自己“哪一步错”、“为什么错”;再让做对的学生帮助补充、更正,必要时让冒尖生代替老师点拨.如果学生说得对的,教师只给肯定,不必重复讲;如果所有学生都说不对的或说不全的,教师就该讲,而且要讲好,一定要让每一位学生真正解决疑难问题,既能理解、懂得“为什么”,又能灵活运用.
(2)若未全对的人数多,则不收未全对的试卷,改为教师逐项提问,让做错的学生举手说出“哪里错”,大家讨论“为什么错”,老师作必要的补充、点拨.
4.教师把学生做错的题分类放在展示台上,白板出示,集体纠错,学生说不完整的,教师补充.
预计出现的错误:
1.写几边形时,数字没有写成汉字;
2.计算错误;
(二)拓展
过渡语:老师还想考一考大家是否真的掌握了
拓展题:.若正n边形的一个外角不大于40°,则它的边数是(
)
A.
n
=
8
B.
n
=
9
C.
n
>9且n为整数
D.
n≥9且n为整数
(三)学生默读课本,自背、互背,达到堂清.
六、课堂作业
过渡语:同学们,运用新知识做作业时,要避免检测时出现的错误.
当堂训练题
1.过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的内角和是(
)
A.360°
B.720°
C.1800°
D.1440°
2.
一个多边形的内角和是1620°,则这个多边形是
边形.
3.周长为72
且内角和为1080°的正n边形的边长为____.
4.如图,在四边形ABCD中,∠A=∠C,∠B=∠D,AB与CD有怎样的位置关系?为什么?BC与AD呢?
5.如图,五边形ABCDE的内角都相等,且∠1
=
∠2,∠3=∠4,求x的值.
拓展题:
如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=
70 ,则∠AED的度数是
.
七、教学反思
