2021-2022学年度人教版数学八年级上册 12.2全等三角形的判定(2)学案(无答案)
文档属性
| 名称 | 2021-2022学年度人教版数学八年级上册 12.2全等三角形的判定(2)学案(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 157.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 10:05:21 | ||
图片预览

文档简介
12.2全等三角形的判定(2)
【学习目标】
理解、识记并能正确运用三角形全等的判定定理SAS.
【学习过程】
一、板书课题,揭示目标
导入语:同学们,今天我们继续学习全等三角形的另一个判定定理--SAS.
本节课的学习目标是什么呢?请看投影
二、
出示学习目标
过渡语:怎样才能当堂达到学习目标呢?请同学们按照指导认真自学.
出示自学指导
自学指导
认真看课本(P37—P39练习前),要求:
1.按照“探究3”的要求动手作图,两个三角形全等吗?
和
分别相等的两个三角形全等(可以简写成“
”或“
”).
2.注意例2的解题格式和步骤,思考运用SAS定理时需要哪些条件,如何正确书写.
3.动手作图,思考有两边和其中一边的对角分别相等的两个三角形
全等.
如有疑问,可小声问同桌或举手问老师.
6分钟后,比谁正确作图,能运用SAS定理证明两个三角形全等.
四、学生自学
过渡语:自学指导明确的同学请举手?自学竞赛开始!
1.学生看书,教师巡视全班,督促每一位学生认真、紧张地自学.
2.检测
提问:
已知△ABC,画△A′B′C′,使A′B′=AB,A′C′=AC,∠A′
=∠A,△ABC和
△A′B′C′全等吗 (学生说一步,教师动画演示一步).
2.AB=DE,∠A=∠D,AC=DF,则△ABC≌
△DEF
,判断的依据是
SAS
.(字母简写即可),用几何语言如何表示.(师强调书写:夹角放在条件的中间位置)
看书上P39思考题,探究“SSA”能否判定两三角形全等?为什么?
判断:
如2图所示,若AB=DE,∠A=∠D,BC=EF,则△ABC≌△DEF.(
)
过渡语:同学们,我们已经知道,两边和它们的夹角分别相等的两个三角形全等,那么就让我们正确运用SAS定理证明两个三角形全等吧.
自学检测题
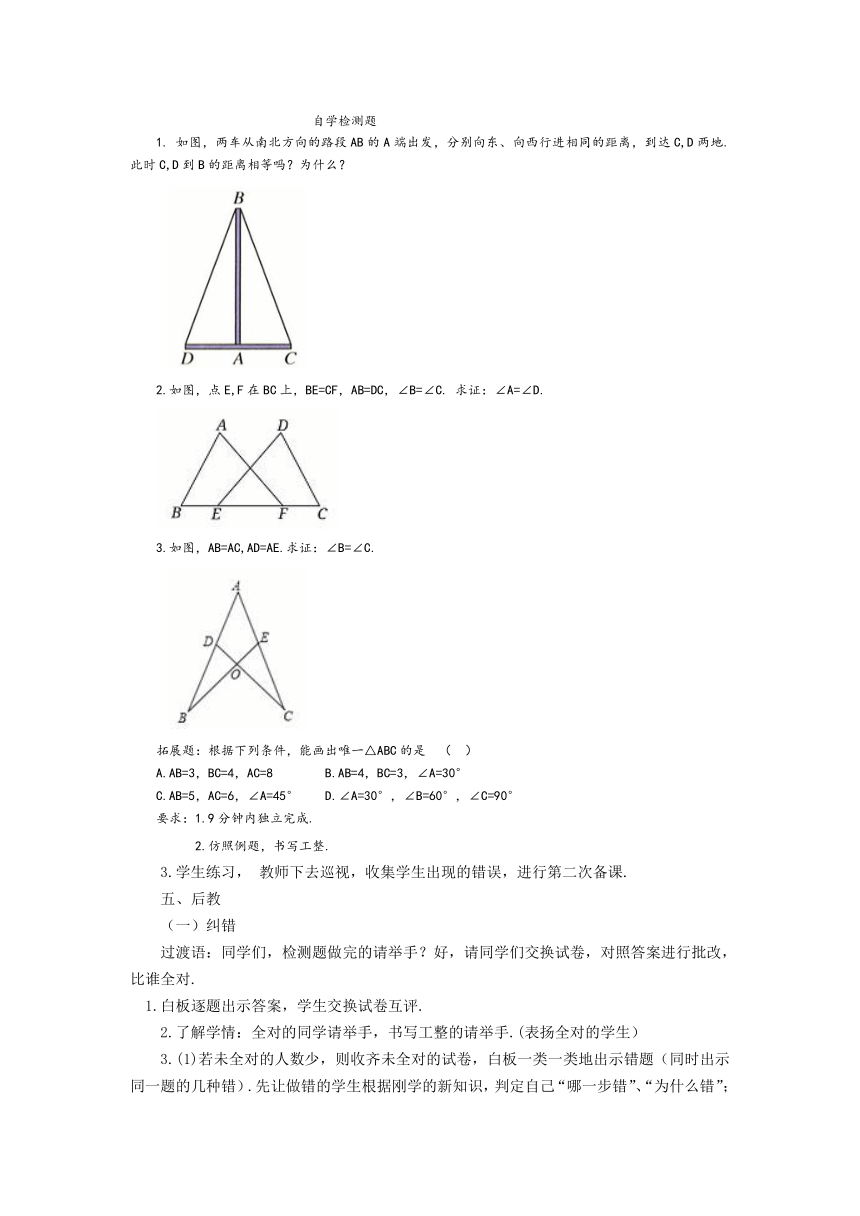
1.
如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地.此时C,D到B的距离相等吗?为什么?
2.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.
求证:∠A=∠D.
3.如图,AB=AC,AD=AE.求证:∠B=∠C.
拓展题:根据下列条件,能画出唯一△ABC的是
(
)
A.AB=3,BC=4,AC=8
B.AB=4,BC=3,∠A=30°
C.AB=5,AC=6,∠A=45°
D.∠A=30°,∠B=60°,∠C=90°
要求:1.9分钟内独立完成.
2.仿照例题,书写工整.
3.学生练习,
教师下去巡视,收集学生出现的错误,进行第二次备课.
五、后教
(一)纠错
过渡语:同学们,检测题做完的请举手?好,请同学们交换试卷,对照答案进行批改,比谁全对.
1.白板逐题出示答案,学生交换试卷互评.
2.了解学情:全对的同学请举手,书写工整的请举手.(表扬全对的学生)
3.(1)若未全对的人数少,则收齐未全对的试卷,白板一类一类地出示错题(同时出示同一题的几种错).先让做错的学生根据刚学的新知识,判定自己“哪一步错”、“为什么错”;再让做对的学生帮助补充、更正,必要时让冒尖生代替老师点拨.如果学生说得对的,教师只给肯定,不必重复讲;如果所有学生都说不对的或说不全的,教师就该讲,而且要讲好,一定要让每一位学生真正解决疑难问题,既能理解、懂得“为什么”,又能灵活运用.
(2)若未全对的人数多,则不收未全对的试卷,改为教师逐项提问,让做错的学生举手说出“哪里错”,大家讨论“为什么错”,老师作必要的补充、点拨.
4.重点讨论第1题和第3题(白板展示相关错题).
老师把学生做错的题分类放到展示台上,白板出示.先让做错的学生说说自己错在哪里?如果不会,再让做对的同学说说错在哪里?为什么?(不出示、不讨论做对的题)
预计会出现的错误:
第1题:找不到题中的隐含条件;
第3题:找不到∠A是公共角这个条件.
(二)口答
过渡语:同学们,接下来老师来考一考大家,比谁答的又对又快!
某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去,能试着说明理由吗?
(三)学生默读课本,自背、互背,达到堂清.
六、当堂训练
过渡语:同学们,运用新知识做作业时,一定要把夹角放在条件的中间位置,要避免检测时出现的错误.
当堂训练题
1.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量哪些量?为什么?
2.如图,AC和BD相交于点O,OA=OC,OB=OD,求证:DC//AB
3.
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,找出图中的全等三角形,并证明他们全等.
拓展题:如图:AD∥BC,且AD=BC,点E,A,C,F在同一条直线上,AE=CF.求证:DE∥BF.
七、教学反思:
【学习目标】
理解、识记并能正确运用三角形全等的判定定理SAS.
【学习过程】
一、板书课题,揭示目标
导入语:同学们,今天我们继续学习全等三角形的另一个判定定理--SAS.
本节课的学习目标是什么呢?请看投影
二、
出示学习目标
过渡语:怎样才能当堂达到学习目标呢?请同学们按照指导认真自学.
出示自学指导
自学指导
认真看课本(P37—P39练习前),要求:
1.按照“探究3”的要求动手作图,两个三角形全等吗?
和
分别相等的两个三角形全等(可以简写成“
”或“
”).
2.注意例2的解题格式和步骤,思考运用SAS定理时需要哪些条件,如何正确书写.
3.动手作图,思考有两边和其中一边的对角分别相等的两个三角形
全等.
如有疑问,可小声问同桌或举手问老师.
6分钟后,比谁正确作图,能运用SAS定理证明两个三角形全等.
四、学生自学
过渡语:自学指导明确的同学请举手?自学竞赛开始!
1.学生看书,教师巡视全班,督促每一位学生认真、紧张地自学.
2.检测
提问:
已知△ABC,画△A′B′C′,使A′B′=AB,A′C′=AC,∠A′
=∠A,△ABC和
△A′B′C′全等吗 (学生说一步,教师动画演示一步).
2.AB=DE,∠A=∠D,AC=DF,则△ABC≌
△DEF
,判断的依据是
SAS
.(字母简写即可),用几何语言如何表示.(师强调书写:夹角放在条件的中间位置)
看书上P39思考题,探究“SSA”能否判定两三角形全等?为什么?
判断:
如2图所示,若AB=DE,∠A=∠D,BC=EF,则△ABC≌△DEF.(
)
过渡语:同学们,我们已经知道,两边和它们的夹角分别相等的两个三角形全等,那么就让我们正确运用SAS定理证明两个三角形全等吧.
自学检测题
1.
如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地.此时C,D到B的距离相等吗?为什么?
2.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.
求证:∠A=∠D.
3.如图,AB=AC,AD=AE.求证:∠B=∠C.
拓展题:根据下列条件,能画出唯一△ABC的是
(
)
A.AB=3,BC=4,AC=8
B.AB=4,BC=3,∠A=30°
C.AB=5,AC=6,∠A=45°
D.∠A=30°,∠B=60°,∠C=90°
要求:1.9分钟内独立完成.
2.仿照例题,书写工整.
3.学生练习,
教师下去巡视,收集学生出现的错误,进行第二次备课.
五、后教
(一)纠错
过渡语:同学们,检测题做完的请举手?好,请同学们交换试卷,对照答案进行批改,比谁全对.
1.白板逐题出示答案,学生交换试卷互评.
2.了解学情:全对的同学请举手,书写工整的请举手.(表扬全对的学生)
3.(1)若未全对的人数少,则收齐未全对的试卷,白板一类一类地出示错题(同时出示同一题的几种错).先让做错的学生根据刚学的新知识,判定自己“哪一步错”、“为什么错”;再让做对的学生帮助补充、更正,必要时让冒尖生代替老师点拨.如果学生说得对的,教师只给肯定,不必重复讲;如果所有学生都说不对的或说不全的,教师就该讲,而且要讲好,一定要让每一位学生真正解决疑难问题,既能理解、懂得“为什么”,又能灵活运用.
(2)若未全对的人数多,则不收未全对的试卷,改为教师逐项提问,让做错的学生举手说出“哪里错”,大家讨论“为什么错”,老师作必要的补充、点拨.
4.重点讨论第1题和第3题(白板展示相关错题).
老师把学生做错的题分类放到展示台上,白板出示.先让做错的学生说说自己错在哪里?如果不会,再让做对的同学说说错在哪里?为什么?(不出示、不讨论做对的题)
预计会出现的错误:
第1题:找不到题中的隐含条件;
第3题:找不到∠A是公共角这个条件.
(二)口答
过渡语:同学们,接下来老师来考一考大家,比谁答的又对又快!
某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去,能试着说明理由吗?
(三)学生默读课本,自背、互背,达到堂清.
六、当堂训练
过渡语:同学们,运用新知识做作业时,一定要把夹角放在条件的中间位置,要避免检测时出现的错误.
当堂训练题
1.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量哪些量?为什么?
2.如图,AC和BD相交于点O,OA=OC,OB=OD,求证:DC//AB
3.
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,找出图中的全等三角形,并证明他们全等.
拓展题:如图:AD∥BC,且AD=BC,点E,A,C,F在同一条直线上,AE=CF.求证:DE∥BF.
七、教学反思:
