2021-2022学年度人教版数学八年级上册13.3.1 等腰三角形(1)学案 (无答案)
文档属性
| 名称 | 2021-2022学年度人教版数学八年级上册13.3.1 等腰三角形(1)学案 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 10:31:51 | ||
图片预览


文档简介
13.3.1
等腰三角形(1)
【学习目标】
理解并识记等腰三角形的定义及其性质,并会正确运用.
【学习过程】
一、板书课题,揭示目标
导入语:同学们,等腰三角形是常见的三角形,它有什么性质呢?今天我们学习13.3.1
等腰三角形(1)(板书课题),本节课的学习目标是什么呢?请看投影
二、
出示学习目标
过渡语:怎样才能当堂达到学习目标呢?请同学们按照指导认真自学.
三、
出示自学指导
自学指导
认真看课本P75—P77练习上面.要求:
1.
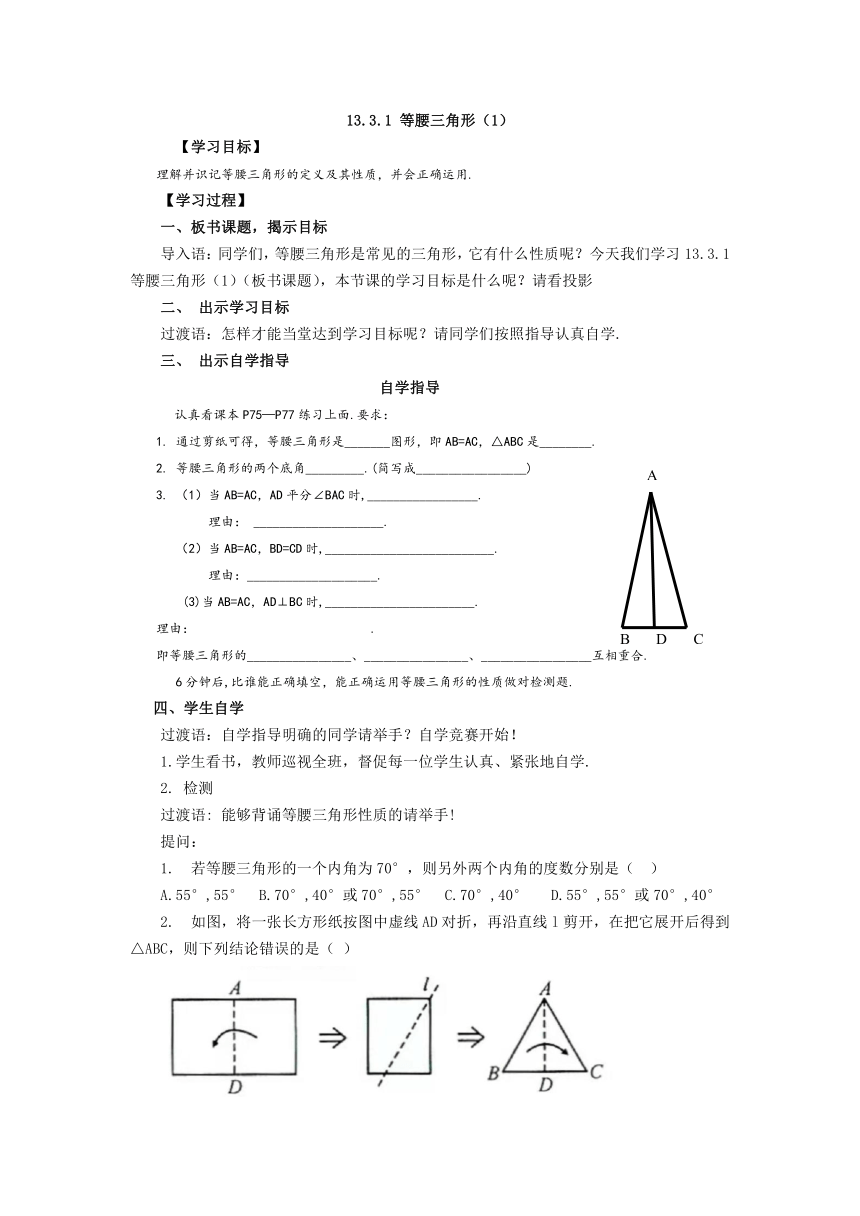
通过剪纸可得,等腰三角形是_______图形,即AB=AC,△ABC是________.
2.
等腰三角形的两个底角_________.(简写成_________________)
3.
(1)当AB=AC,AD平分∠BAC时,_________________.
理由:
____________________.
(2)当AB=AC,BD=CD时,__________________________.
理由:____________________.
(3)当AB=AC,AD⊥BC时,_______________________.
理由:
.
即等腰三角形的________________、________________、_________________互相重合.
6分钟后,比谁能正确填空,能正确运用等腰三角形的性质做对检测题.
四、学生自学
过渡语:自学指导明确的同学请举手?自学竞赛开始!
1.学生看书,教师巡视全班,督促每一位学生认真、紧张地自学.
2.
检测
过渡语:
能够背诵等腰三角形性质的请举手!
提问:
若等腰三角形的一个内角为70°,则另外两个内角的度数分别是(
)
A.55°,55°
B.70°,40°或70°,55°
C.70°,40°
D.55°,55°或70°,40°
如图,将一张长方形纸按图中虚线AD对折,再沿直线l剪开,在把它展开后得到△ABC,则下列结论错误的是(
)
A.AD⊥BC
B.BD=CD
C.∠B=∠C
D.AB=CB
1.等腰三角形的两个底角相等.(简写成“等角对等边”)
2.等腰三角形的顶角平分线,底边上的中线、底边上的高相互重合(简写成“三线合一”)
师强调:等腰三角形的三线合一非常重要,等腰三角形是轴对称图形.
过渡语:同学们,
等腰三角形的性质都会背了,下面,大家就运用等腰三角形性质做检测题
自学检测题
1.如图,在下列等腰三角形中,分别求出它们底角的度数.__________,__________
2.如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高.标出∠B,∠C,∠BAD,∠DAC的度数_____,_____,______,____,并写出图中所有相等的线段____________________________.
3.如图3,在△
ABC中,AB=AD=DC,
∠
BAD=260.求∠
B和∠
C的度数.
拓展题:如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为_________
要求:1.6分钟内独立完成.
2.仿照例题,比谁做得又对又快.
3.学生练习,
教师下去巡视,收集学生出现的错误,进行第二次备课.
五、后教
(一)纠错
过渡语:同学们,检测题做完的请举手?好,请交换练习纸,对照答案互评,比谁全对.
1.白板逐题出示答案,学生交换试卷互评.
2.了解学情:全对的同学请举手,书写工整的请举手,好!
3.(1)若未全对的人数少,则收齐未全对的试卷,白板一类一类地出示错题(同时出示同一题的几种错).先让做错的学生根据刚学的新知识,判定自己“哪一步错”、“为什么错”;再让做对的学生帮助补充、更正,必要时让冒尖生代替老师点拨.如果学生说得对的,教师只给肯定,不必重复讲;如果所有学生都说不对的或说不全的,教师就该讲,而且要讲好,一定要让每一位学生真正解决疑难问题,既能理解、懂得“为什么”,又能灵活运用.
(2)若未全对的人数多,则不收未全对的试卷,改为教师逐项提问,让做错的学生举手说出“哪里错”,大家讨论“为什么错”,老师作必要的补充、点拨.
4.教师把学生做错的题分类放在展示台上,白板出示,集体纠错,学生说不完整的,教师补充.
预计会出现的错误:
第3题:
1.方法复杂(用全等),不会运用等腰三角形性质.
2.计算出错.
(二)学生默读课本,自背、互背,达到堂清.
六、当堂训练
过渡语:同学们,运用新知识做作业时,要避免检测时出现的错误.
当堂训练题
1.(1)等腰三角形的顶角是110°时,其余两个角是____,____
(2)等腰三角形的底角是110°时,它的另外两个角________________
2.如图,厂房屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥BC,且顶角∠BAC=120°.∠B=___
∠C=___
∠BAD=___
∠CAD=___
3.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.求证BD=CE.
4.如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.求∠DBC的度数.
拓展题:已知平面直角坐标系中,点A的坐标为(-2,3),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有____________个.
七、教学反思:
等腰三角形(1)
【学习目标】
理解并识记等腰三角形的定义及其性质,并会正确运用.
【学习过程】
一、板书课题,揭示目标
导入语:同学们,等腰三角形是常见的三角形,它有什么性质呢?今天我们学习13.3.1
等腰三角形(1)(板书课题),本节课的学习目标是什么呢?请看投影
二、
出示学习目标
过渡语:怎样才能当堂达到学习目标呢?请同学们按照指导认真自学.
三、
出示自学指导
自学指导
认真看课本P75—P77练习上面.要求:
1.
通过剪纸可得,等腰三角形是_______图形,即AB=AC,△ABC是________.
2.
等腰三角形的两个底角_________.(简写成_________________)
3.
(1)当AB=AC,AD平分∠BAC时,_________________.
理由:
____________________.
(2)当AB=AC,BD=CD时,__________________________.
理由:____________________.
(3)当AB=AC,AD⊥BC时,_______________________.
理由:
.
即等腰三角形的________________、________________、_________________互相重合.
6分钟后,比谁能正确填空,能正确运用等腰三角形的性质做对检测题.
四、学生自学
过渡语:自学指导明确的同学请举手?自学竞赛开始!
1.学生看书,教师巡视全班,督促每一位学生认真、紧张地自学.
2.
检测
过渡语:
能够背诵等腰三角形性质的请举手!
提问:
若等腰三角形的一个内角为70°,则另外两个内角的度数分别是(
)
A.55°,55°
B.70°,40°或70°,55°
C.70°,40°
D.55°,55°或70°,40°
如图,将一张长方形纸按图中虚线AD对折,再沿直线l剪开,在把它展开后得到△ABC,则下列结论错误的是(
)
A.AD⊥BC
B.BD=CD
C.∠B=∠C
D.AB=CB
1.等腰三角形的两个底角相等.(简写成“等角对等边”)
2.等腰三角形的顶角平分线,底边上的中线、底边上的高相互重合(简写成“三线合一”)
师强调:等腰三角形的三线合一非常重要,等腰三角形是轴对称图形.
过渡语:同学们,
等腰三角形的性质都会背了,下面,大家就运用等腰三角形性质做检测题
自学检测题
1.如图,在下列等腰三角形中,分别求出它们底角的度数.__________,__________
2.如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高.标出∠B,∠C,∠BAD,∠DAC的度数_____,_____,______,____,并写出图中所有相等的线段____________________________.
3.如图3,在△
ABC中,AB=AD=DC,
∠
BAD=260.求∠
B和∠
C的度数.
拓展题:如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为_________
要求:1.6分钟内独立完成.
2.仿照例题,比谁做得又对又快.
3.学生练习,
教师下去巡视,收集学生出现的错误,进行第二次备课.
五、后教
(一)纠错
过渡语:同学们,检测题做完的请举手?好,请交换练习纸,对照答案互评,比谁全对.
1.白板逐题出示答案,学生交换试卷互评.
2.了解学情:全对的同学请举手,书写工整的请举手,好!
3.(1)若未全对的人数少,则收齐未全对的试卷,白板一类一类地出示错题(同时出示同一题的几种错).先让做错的学生根据刚学的新知识,判定自己“哪一步错”、“为什么错”;再让做对的学生帮助补充、更正,必要时让冒尖生代替老师点拨.如果学生说得对的,教师只给肯定,不必重复讲;如果所有学生都说不对的或说不全的,教师就该讲,而且要讲好,一定要让每一位学生真正解决疑难问题,既能理解、懂得“为什么”,又能灵活运用.
(2)若未全对的人数多,则不收未全对的试卷,改为教师逐项提问,让做错的学生举手说出“哪里错”,大家讨论“为什么错”,老师作必要的补充、点拨.
4.教师把学生做错的题分类放在展示台上,白板出示,集体纠错,学生说不完整的,教师补充.
预计会出现的错误:
第3题:
1.方法复杂(用全等),不会运用等腰三角形性质.
2.计算出错.
(二)学生默读课本,自背、互背,达到堂清.
六、当堂训练
过渡语:同学们,运用新知识做作业时,要避免检测时出现的错误.
当堂训练题
1.(1)等腰三角形的顶角是110°时,其余两个角是____,____
(2)等腰三角形的底角是110°时,它的另外两个角________________
2.如图,厂房屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥BC,且顶角∠BAC=120°.∠B=___
∠C=___
∠BAD=___
∠CAD=___
3.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.求证BD=CE.
4.如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.求∠DBC的度数.
拓展题:已知平面直角坐标系中,点A的坐标为(-2,3),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有____________个.
七、教学反思:
