河北省唐山市第十高中2022届高三上学期第一周模拟测试数学试题(Word版含答案)
文档属性
| 名称 | 河北省唐山市第十高中2022届高三上学期第一周模拟测试数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 930.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 00:00:00 | ||
图片预览




文档简介
河北省唐山市唐山第十中学2021-2022学年高三数学第一周模拟测试试题
(考试时间:120分钟
总分:150分)
第Ⅰ部分(选择题,共60分)
一、单选题(本大题共8小题,每小题5分,共40分.四个选项中只有一项符合题目要求.)
1.(2021年全国新高考Ⅰ卷数学试题)设集合,,则(
)
A.
B.
C.
D.
2.(2021年全国高考甲卷数学(理)试题)已知,则(
)
A.
B.
C.
D.
3.(2021年全国高考乙卷数学(文)试题)已知命题﹔命题﹐,则下列命题中为真命题的是(
)
A.
B.
C.
D.
4.设,,,则(
)
A.
B.
C.
D.
5.已知AD,BE分别为的边BC,AC上的中线,设,则(
)
A.
B.
C.
D.
6.电影《你好,李焕英》在2021年正月初一正式上映,一对夫妇带着他们的两个孩子去观看该影片,订购的4张电影票恰好在同一排且连在一起.
为安全起见,影院要求每个孩子都至少有一位家长相邻陪坐,则不同的坐法种数是(
)
A.20
B.16
C.12
D.8
7.已知的终边在第四象限,若,则(
)
A.
B.
C.
D.
8.已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A.
B.
C.
D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.设随机变量的分布列为,则(
)
A.
B.
C.
D.
10.已知,是椭圆的左、右焦点,是椭圆上一点,则(
)
A.当时,满足的点有2个
B.当时,满足的点有4个
C.的周长小于
D.的面积大于等于
11.已知函数,则下列说法正确的是(
)
A.函数的周期为
B.函数图象的一条对称轴为直线
C.函数在上单调递增
D.函数的最小值为
12.如图,在三棱锥中,,,,,且到平面的距离为1,则下列说法正确的是(
)
A.三棱锥的体积为
B.与所成角的大小为60°
C.
D.三棱锥外接球的表面积为
三、填空题:本题共4小题,每小题5分,共20分。
13.轴截面是直角三角形的圆锥的底面半径为,则其轴截面面积为________.
14.已知是定义在上的奇函数,且当时,,则的值为___________.
15.已知函数,则曲线在处的切线方程为___________.
16.的内角的对边分别为,若,则_______,的最大值是________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知等差数列的前项和为,,,数列的前项和.
(1)求数列和的通项公式;
(2)若数列满足,求数列的前项和.
18.在中,角的对边分别为,若,且.
(1)求角的值;
(2)若,且的面积为,求边上的中线的长.
19.已知:如图,在四棱锥中,四边形为正方形,面,且,为中点.
(1)证明:平面;
(2)证明:平面平面;
(3)求二面角的正弦值.
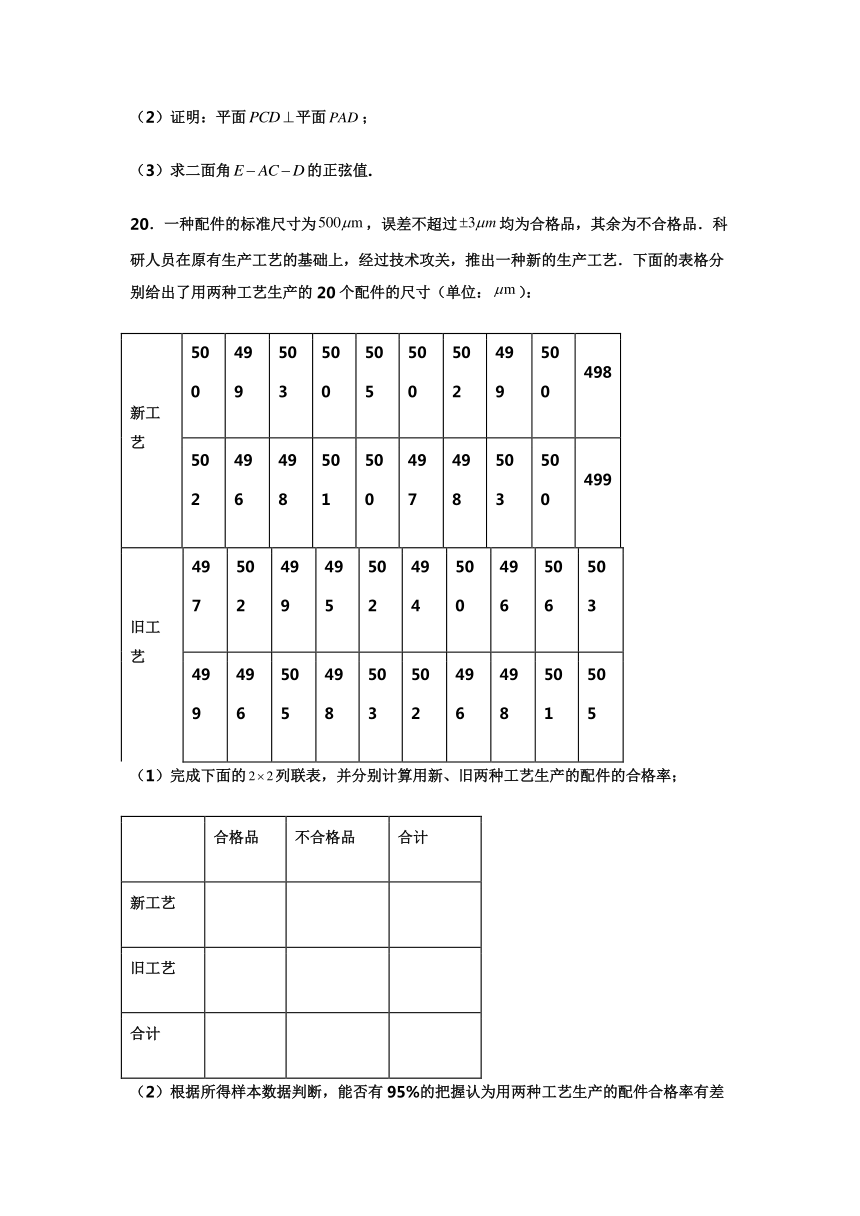
20.一种配件的标准尺寸为,误差不超过均为合格品,其余为不合格品.科研人员在原有生产工艺的基础上,经过技术攻关,推出一种新的生产工艺.下面的表格分别给出了用两种工艺生产的20个配件的尺寸(单位:):
新工艺
500
499
503
500
505
500
502
499
500
498
502
496
498
501
500
497
498
503
500
499
旧工艺
497
502
499
495
502
494
500
496
506
503
499
496
505
498
503
502
496
498
501
505
(1)完成下面的列联表,并分别计算用新、旧两种工艺生产的配件的合格率;
合格品
不合格品
合计
新工艺
旧工艺
合计
(2)根据所得样本数据判断,能否有95%的把握认为用两种工艺生产的配件合格率有差异?
,
0.15
0.050
0.025
0.005
2.072
3.841
5.024
7.879
21.双曲线的一条渐近线方程是,坐标原点到直线的距离为,其中,.
(1)求双曲线的方程;
(2)若是双曲线虚轴在轴正半轴上的端点,过点作直线交双曲线于点,,求时,直线的方程.
22.已知函数.
(1)讨论函数的单调性;
(2)若恒成立,求正实数的取值范围.
2022年高考高三数学模拟测试卷答案
一、单选题(本大题共8小题,每小题5分,共40分.四个选项中只有一项符合题目要求.)
1.(2021年全国新高考Ⅰ卷数学试题)设集合,,则(
)
A.
B.
C.
D.
【答案】B
【解】由题设有,故选:B
.
2.(2021年全国高考甲卷数学(理)试题)已知,则(
)
A.
B.
C.
D.
【答案】B,
.
故选:B.
3.(2021年全国高考乙卷数学(文)试题)已知命题﹔命题﹐,则下列命题中为真命题的是(
)
A.
B.
C.
D.
【答案】A
【解】由于,所以命题为真命题;
由于,所以,所以命题为真命题;
所以为真命题,、、为假命题.
故选:A.
4.设,,,则(
)
A.
B.
C.
D.
【答案】A
【解】
令,
因为在上单调递增,
所以在上单调递增,
所以,,
所以,且,
因为在上单调递增,所以,
所以,
故选:A.
5.已知AD,BE分别为的边BC,AC上的中线,设,则(
)
A.
B.
C.
D.
【答案】B
【解】
∵
AD为边BC上的中线,
∴
,
又BE为边AC上的中线,
∴
,
又,
∴
,
∴,
故选:B.
6.电影《你好,李焕英》在2021年正月初一正式上映,一对夫妇带着他们的两个孩子去观看该影片,订购的4张电影票恰好在同一排且连在一起.
为安全起见,影院要求每个孩子都至少有一位家长相邻陪坐,则不同的坐法种数是(
)
A.20
B.16
C.12
D.8
【答案】B
【解】
①
②
③
④
若家长在①③,则方法数有种,
若家长在①④,则方法数有种,
若家长在②③,则方法数有种,
若家长在②④,则方法数有种,
故总的方法数有种.
故选:B
7.已知的终边在第四象限,若,则(
)
A.
B.
C.
D.
【答案】A
【解】
的终边在第四象限,,
所以,
则.
故选:A
8.(2021·全国高三专题练习(文))已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A.
B.
C.
D.
【答案】B
【解】法一:如图,由已知可设,则,由椭圆的定义有.在中,由余弦定理推论得.在中,由余弦定理得,解得.
所求椭圆方程为,故选B.
法二:由已知可设,则,由椭圆的定义有.在和中,由余弦定理得,又互补,,两式消去,得,解得.所求椭圆方程为,故选B.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.设随机变量的分布列为,则(
)
A.
B.
C.
D.
【答案】AB
【解】
对于选项A,∵随机变量的分布列为,,解得,故A正确;
对于选项B,易知,故B正确;
对于选项C,易知,故C错误;
对于选项D,易知,故D错误.
故选:AB.
10.已知,是椭圆的左、右焦点,是椭圆上一点,则(
)
A.当时,满足的点有2个
B.当时,满足的点有4个
C.的周长小于
D.的面积大于等于
【答案】ABC
【解】
对于选项A和选项B,当点的坐标为或时,
最大,且当时,,易知选项A和B正确;
对于选项C,的周长为,故选项C正确;
对于选项D,的面积为,故选项D错误.
故选:ABC.
11.已知函数,则下列说法正确的是(
)
A.函数的周期为
B.函数图象的一条对称轴为直线
C.函数在上单调递增
D.函数的最小值为
【答案】ABD
【解】
解:函数
.
所以函数的周期为,故A选项正确;
当时,,所以直线是函数图象的一条对称轴,故B选项正确;
当,则,由正弦函数性质可知,此时单调递减,故C选项错误;
由可知,当时,取得最小值为,故D选项正确.
故选:ABD.
12.如图,在三棱锥中,,,,,且到平面的距离为1,则下列说法正确的是(
)
A.三棱锥的体积为
B.与所成角的大小为60°
C.
D.三棱锥外接球的表面积为
【答案】ACD
【分析】
【解】
取AC中点O,连接PO,BO.如图,
因为BC=BA,O是AC中点,所以AC⊥BO,又因为AC⊥PB,所以AC⊥平面POB.
过P点作BO的垂线,交BO的延长线于D,则AC⊥PD,所以PD⊥平面ABC,
所以PD=1,又因为,所以BD=;
结合条件BC=BA=1,AB⊥BC可知四边形ABCD为正方形,且P,A,B,C,D在边长为1的正方体上.
结合正方体的性质,,A选项说法正确.
因为AB∥CD,PC与DC所成角为45°,所以AB与PC所成角的大小为45°,B选项错误;
因为BC⊥平面PDC,所以BC⊥PC,C选项正确;
三棱锥P﹣ABC外接球即为正方体的外接球,PB为直径,所以表面积为,D选项正确.
故选:ACD
三、填空题:本题共4小题,每小题5分,共20分。
13.轴截面是直角三角形的圆锥的底面半径为,则其轴截面面积为________.
【答案】
【解】
由圆锥的结构特征可知,轴截面为等腰直角三角形,其高为,
所以.
故答案为:
14.已知是定义在上的奇函数,且当时,,则的值为___________.
【答案】
【解】
因为是定义在上的奇函数,则,
又,
所以.
故答案为:6
15.已知函数,则曲线在处的切线方程为___________.
【答案】
【解】
所以,
又,
所以曲线在处的切线方程为,即.
故答案为:
16.的内角的对边分别为,若,则_______,的最大值是________.
【答案】
(1).
(2).
【解】,
,
;
由于求的最大值,只需考虑的情况,
所以,等号成立当且仅当.
故答案为:
;.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知等差数列的前项和为,,,数列的前项和.
(1)求数列和的通项公式;
(2)若数列满足,求数列的前项和.
【答案】(1);;(2).
【解】
(1)设等差数列的公差为,∵,,
∴,,
解得:,
.
的项和,
当时,,,也符合上式.
∴.
(2),
∴数列的前项和
.
18.在中,角的对边分别为,若,且.
(1)求角的值;
(2)若,且的面积为,求边上的中线的长.
【答案】(1);(2).
【解】
(1)因为,由正弦定理得,
,,.又,所以,可得.
(2)由(1)知,若,则,,
,,(舍).
又在中,
所以.
19.已知:如图,在四棱锥中,四边形为正方形,面,且,为中点.
(1)证明:平面;
(2)证明:平面平面;
(3)求二面角的正弦值.
【答案】(1)证明见解析;(2)证明见解析;(3).
【解】
(1)证明:连接交于点,连接,则为的中点,
因为为的中点,,
平面,平面,因此,平面;
(2)证明:平面,平面,,
在正方形中,,且,所以,平面.
又平面,所以,平面平面.
(3)解:平面,且,
如图,以为坐标原点,、、所在直线分别为轴、轴、轴建立空间直角坐标系.
,所以,、、、、、.
易知平面的一个法向量为,
设平面的一个法向量为,,,
则,即,令,则,,解得.
,则,
因此,二面角的正弦值为.
20.一种配件的标准尺寸为,误差不超过均为合格品,其余为不合格品.科研人员在原有生产工艺的基础上,经过技术攻关,推出一种新的生产工艺.下面的表格分别给出了用两种工艺生产的20个配件的尺寸(单位:):
新工艺
500
499
503
500
505
500
502
499
500
498
502
496
498
501
500
497
498
503
500
499
旧工艺
497
502
499
495
502
494
500
496
506
503
499
496
505
498
503
502
496
498
501
505
(1)完成下面的列联表,并分别计算用新、旧两种工艺生产的配件的合格率;
合格品
不合格品
合计
新工艺
旧工艺
合计
(2)根据所得样本数据判断,能否有95%的把握认为用两种工艺生产的配件合格率有差异?
,
0.15
0.050
0.025
0.005
2.072
3.841
5.024
7.879
【答案】(1)填表见解析;新工艺生产的配件的合格率:,用旧工艺生产的配件的合格率:;(2)有95%的把握认为用两种工艺生产的配件合格率有差异.
【解】
(1)列联表如下:
合格品
不合格品
合计
新工艺
18
2
20
旧工艺
12
8
20
合计
30
10
40
新工艺生产的配件的合格率:,
用旧工艺生产的配件的合格率:.
(2),
因为,
所以,根据所得样本数据判断,有95%的把握认为用两种工艺生产的配件合格率有差异.
21.双曲线的一条渐近线方程是,坐标原点到直线的距离为,其中,.
(1)求双曲线的方程;
(2)若是双曲线虚轴在轴正半轴上的端点,过点作直线交双曲线于点,,求时,直线的方程.
【答案】(1);(2).
【解】
(1)设直线:,由题意,
,∴,∴双曲线方程为.
(2)由(1)得,,设,,设直线:,
∴,
∴,整理得,(1)
∴,,
,.
∵,,,
∴,即,
解得,∴代入(1)有解,∴:.
22.已知函数.
(1)讨论函数的单调性;
(2)若恒成立,求正实数的取值范围.
【答案】(1)答案见解析;(2).
【解】
(1)且,
∴时,即单调递增;
时,有,即在上单调递增;有,即在上单调递减;
综上,时在上单调递增;时在上单调递减,在上单调递增;
(2)由题设,,即恒成立,
令,则,
∴由(1)知:时有极小值也是最小值,故只需即可.
若,则,即在上递减,又,
∴时,,即恒成立.
∴正实数的范围为.
(考试时间:120分钟
总分:150分)
第Ⅰ部分(选择题,共60分)
一、单选题(本大题共8小题,每小题5分,共40分.四个选项中只有一项符合题目要求.)
1.(2021年全国新高考Ⅰ卷数学试题)设集合,,则(
)
A.
B.
C.
D.
2.(2021年全国高考甲卷数学(理)试题)已知,则(
)
A.
B.
C.
D.
3.(2021年全国高考乙卷数学(文)试题)已知命题﹔命题﹐,则下列命题中为真命题的是(
)
A.
B.
C.
D.
4.设,,,则(
)
A.
B.
C.
D.
5.已知AD,BE分别为的边BC,AC上的中线,设,则(
)
A.
B.
C.
D.
6.电影《你好,李焕英》在2021年正月初一正式上映,一对夫妇带着他们的两个孩子去观看该影片,订购的4张电影票恰好在同一排且连在一起.
为安全起见,影院要求每个孩子都至少有一位家长相邻陪坐,则不同的坐法种数是(
)
A.20
B.16
C.12
D.8
7.已知的终边在第四象限,若,则(
)
A.
B.
C.
D.
8.已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A.
B.
C.
D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.设随机变量的分布列为,则(
)
A.
B.
C.
D.
10.已知,是椭圆的左、右焦点,是椭圆上一点,则(
)
A.当时,满足的点有2个
B.当时,满足的点有4个
C.的周长小于
D.的面积大于等于
11.已知函数,则下列说法正确的是(
)
A.函数的周期为
B.函数图象的一条对称轴为直线
C.函数在上单调递增
D.函数的最小值为
12.如图,在三棱锥中,,,,,且到平面的距离为1,则下列说法正确的是(
)
A.三棱锥的体积为
B.与所成角的大小为60°
C.
D.三棱锥外接球的表面积为
三、填空题:本题共4小题,每小题5分,共20分。
13.轴截面是直角三角形的圆锥的底面半径为,则其轴截面面积为________.
14.已知是定义在上的奇函数,且当时,,则的值为___________.
15.已知函数,则曲线在处的切线方程为___________.
16.的内角的对边分别为,若,则_______,的最大值是________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知等差数列的前项和为,,,数列的前项和.
(1)求数列和的通项公式;
(2)若数列满足,求数列的前项和.
18.在中,角的对边分别为,若,且.
(1)求角的值;
(2)若,且的面积为,求边上的中线的长.
19.已知:如图,在四棱锥中,四边形为正方形,面,且,为中点.
(1)证明:平面;
(2)证明:平面平面;
(3)求二面角的正弦值.
20.一种配件的标准尺寸为,误差不超过均为合格品,其余为不合格品.科研人员在原有生产工艺的基础上,经过技术攻关,推出一种新的生产工艺.下面的表格分别给出了用两种工艺生产的20个配件的尺寸(单位:):
新工艺
500
499
503
500
505
500
502
499
500
498
502
496
498
501
500
497
498
503
500
499
旧工艺
497
502
499
495
502
494
500
496
506
503
499
496
505
498
503
502
496
498
501
505
(1)完成下面的列联表,并分别计算用新、旧两种工艺生产的配件的合格率;
合格品
不合格品
合计
新工艺
旧工艺
合计
(2)根据所得样本数据判断,能否有95%的把握认为用两种工艺生产的配件合格率有差异?
,
0.15
0.050
0.025
0.005
2.072
3.841
5.024
7.879
21.双曲线的一条渐近线方程是,坐标原点到直线的距离为,其中,.
(1)求双曲线的方程;
(2)若是双曲线虚轴在轴正半轴上的端点,过点作直线交双曲线于点,,求时,直线的方程.
22.已知函数.
(1)讨论函数的单调性;
(2)若恒成立,求正实数的取值范围.
2022年高考高三数学模拟测试卷答案
一、单选题(本大题共8小题,每小题5分,共40分.四个选项中只有一项符合题目要求.)
1.(2021年全国新高考Ⅰ卷数学试题)设集合,,则(
)
A.
B.
C.
D.
【答案】B
【解】由题设有,故选:B
.
2.(2021年全国高考甲卷数学(理)试题)已知,则(
)
A.
B.
C.
D.
【答案】B,
.
故选:B.
3.(2021年全国高考乙卷数学(文)试题)已知命题﹔命题﹐,则下列命题中为真命题的是(
)
A.
B.
C.
D.
【答案】A
【解】由于,所以命题为真命题;
由于,所以,所以命题为真命题;
所以为真命题,、、为假命题.
故选:A.
4.设,,,则(
)
A.
B.
C.
D.
【答案】A
【解】
令,
因为在上单调递增,
所以在上单调递增,
所以,,
所以,且,
因为在上单调递增,所以,
所以,
故选:A.
5.已知AD,BE分别为的边BC,AC上的中线,设,则(
)
A.
B.
C.
D.
【答案】B
【解】
∵
AD为边BC上的中线,
∴
,
又BE为边AC上的中线,
∴
,
又,
∴
,
∴,
故选:B.
6.电影《你好,李焕英》在2021年正月初一正式上映,一对夫妇带着他们的两个孩子去观看该影片,订购的4张电影票恰好在同一排且连在一起.
为安全起见,影院要求每个孩子都至少有一位家长相邻陪坐,则不同的坐法种数是(
)
A.20
B.16
C.12
D.8
【答案】B
【解】
①
②
③
④
若家长在①③,则方法数有种,
若家长在①④,则方法数有种,
若家长在②③,则方法数有种,
若家长在②④,则方法数有种,
故总的方法数有种.
故选:B
7.已知的终边在第四象限,若,则(
)
A.
B.
C.
D.
【答案】A
【解】
的终边在第四象限,,
所以,
则.
故选:A
8.(2021·全国高三专题练习(文))已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A.
B.
C.
D.
【答案】B
【解】法一:如图,由已知可设,则,由椭圆的定义有.在中,由余弦定理推论得.在中,由余弦定理得,解得.
所求椭圆方程为,故选B.
法二:由已知可设,则,由椭圆的定义有.在和中,由余弦定理得,又互补,,两式消去,得,解得.所求椭圆方程为,故选B.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.设随机变量的分布列为,则(
)
A.
B.
C.
D.
【答案】AB
【解】
对于选项A,∵随机变量的分布列为,,解得,故A正确;
对于选项B,易知,故B正确;
对于选项C,易知,故C错误;
对于选项D,易知,故D错误.
故选:AB.
10.已知,是椭圆的左、右焦点,是椭圆上一点,则(
)
A.当时,满足的点有2个
B.当时,满足的点有4个
C.的周长小于
D.的面积大于等于
【答案】ABC
【解】
对于选项A和选项B,当点的坐标为或时,
最大,且当时,,易知选项A和B正确;
对于选项C,的周长为,故选项C正确;
对于选项D,的面积为,故选项D错误.
故选:ABC.
11.已知函数,则下列说法正确的是(
)
A.函数的周期为
B.函数图象的一条对称轴为直线
C.函数在上单调递增
D.函数的最小值为
【答案】ABD
【解】
解:函数
.
所以函数的周期为,故A选项正确;
当时,,所以直线是函数图象的一条对称轴,故B选项正确;
当,则,由正弦函数性质可知,此时单调递减,故C选项错误;
由可知,当时,取得最小值为,故D选项正确.
故选:ABD.
12.如图,在三棱锥中,,,,,且到平面的距离为1,则下列说法正确的是(
)
A.三棱锥的体积为
B.与所成角的大小为60°
C.
D.三棱锥外接球的表面积为
【答案】ACD
【分析】
【解】
取AC中点O,连接PO,BO.如图,
因为BC=BA,O是AC中点,所以AC⊥BO,又因为AC⊥PB,所以AC⊥平面POB.
过P点作BO的垂线,交BO的延长线于D,则AC⊥PD,所以PD⊥平面ABC,
所以PD=1,又因为,所以BD=;
结合条件BC=BA=1,AB⊥BC可知四边形ABCD为正方形,且P,A,B,C,D在边长为1的正方体上.
结合正方体的性质,,A选项说法正确.
因为AB∥CD,PC与DC所成角为45°,所以AB与PC所成角的大小为45°,B选项错误;
因为BC⊥平面PDC,所以BC⊥PC,C选项正确;
三棱锥P﹣ABC外接球即为正方体的外接球,PB为直径,所以表面积为,D选项正确.
故选:ACD
三、填空题:本题共4小题,每小题5分,共20分。
13.轴截面是直角三角形的圆锥的底面半径为,则其轴截面面积为________.
【答案】
【解】
由圆锥的结构特征可知,轴截面为等腰直角三角形,其高为,
所以.
故答案为:
14.已知是定义在上的奇函数,且当时,,则的值为___________.
【答案】
【解】
因为是定义在上的奇函数,则,
又,
所以.
故答案为:6
15.已知函数,则曲线在处的切线方程为___________.
【答案】
【解】
所以,
又,
所以曲线在处的切线方程为,即.
故答案为:
16.的内角的对边分别为,若,则_______,的最大值是________.
【答案】
(1).
(2).
【解】,
,
;
由于求的最大值,只需考虑的情况,
所以,等号成立当且仅当.
故答案为:
;.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知等差数列的前项和为,,,数列的前项和.
(1)求数列和的通项公式;
(2)若数列满足,求数列的前项和.
【答案】(1);;(2).
【解】
(1)设等差数列的公差为,∵,,
∴,,
解得:,
.
的项和,
当时,,,也符合上式.
∴.
(2),
∴数列的前项和
.
18.在中,角的对边分别为,若,且.
(1)求角的值;
(2)若,且的面积为,求边上的中线的长.
【答案】(1);(2).
【解】
(1)因为,由正弦定理得,
,,.又,所以,可得.
(2)由(1)知,若,则,,
,,(舍).
又在中,
所以.
19.已知:如图,在四棱锥中,四边形为正方形,面,且,为中点.
(1)证明:平面;
(2)证明:平面平面;
(3)求二面角的正弦值.
【答案】(1)证明见解析;(2)证明见解析;(3).
【解】
(1)证明:连接交于点,连接,则为的中点,
因为为的中点,,
平面,平面,因此,平面;
(2)证明:平面,平面,,
在正方形中,,且,所以,平面.
又平面,所以,平面平面.
(3)解:平面,且,
如图,以为坐标原点,、、所在直线分别为轴、轴、轴建立空间直角坐标系.
,所以,、、、、、.
易知平面的一个法向量为,
设平面的一个法向量为,,,
则,即,令,则,,解得.
,则,
因此,二面角的正弦值为.
20.一种配件的标准尺寸为,误差不超过均为合格品,其余为不合格品.科研人员在原有生产工艺的基础上,经过技术攻关,推出一种新的生产工艺.下面的表格分别给出了用两种工艺生产的20个配件的尺寸(单位:):
新工艺
500
499
503
500
505
500
502
499
500
498
502
496
498
501
500
497
498
503
500
499
旧工艺
497
502
499
495
502
494
500
496
506
503
499
496
505
498
503
502
496
498
501
505
(1)完成下面的列联表,并分别计算用新、旧两种工艺生产的配件的合格率;
合格品
不合格品
合计
新工艺
旧工艺
合计
(2)根据所得样本数据判断,能否有95%的把握认为用两种工艺生产的配件合格率有差异?
,
0.15
0.050
0.025
0.005
2.072
3.841
5.024
7.879
【答案】(1)填表见解析;新工艺生产的配件的合格率:,用旧工艺生产的配件的合格率:;(2)有95%的把握认为用两种工艺生产的配件合格率有差异.
【解】
(1)列联表如下:
合格品
不合格品
合计
新工艺
18
2
20
旧工艺
12
8
20
合计
30
10
40
新工艺生产的配件的合格率:,
用旧工艺生产的配件的合格率:.
(2),
因为,
所以,根据所得样本数据判断,有95%的把握认为用两种工艺生产的配件合格率有差异.
21.双曲线的一条渐近线方程是,坐标原点到直线的距离为,其中,.
(1)求双曲线的方程;
(2)若是双曲线虚轴在轴正半轴上的端点,过点作直线交双曲线于点,,求时,直线的方程.
【答案】(1);(2).
【解】
(1)设直线:,由题意,
,∴,∴双曲线方程为.
(2)由(1)得,,设,,设直线:,
∴,
∴,整理得,(1)
∴,,
,.
∵,,,
∴,即,
解得,∴代入(1)有解,∴:.
22.已知函数.
(1)讨论函数的单调性;
(2)若恒成立,求正实数的取值范围.
【答案】(1)答案见解析;(2).
【解】
(1)且,
∴时,即单调递增;
时,有,即在上单调递增;有,即在上单调递减;
综上,时在上单调递增;时在上单调递减,在上单调递增;
(2)由题设,,即恒成立,
令,则,
∴由(1)知:时有极小值也是最小值,故只需即可.
若,则,即在上递减,又,
∴时,,即恒成立.
∴正实数的范围为.
同课章节目录
