宁夏银川三沙源上游高中校2020-2021学年高二上学期期末考试数学(理)试题(Word版含简答案)
文档属性
| 名称 | 宁夏银川三沙源上游高中校2020-2021学年高二上学期期末考试数学(理)试题(Word版含简答案) |  | |
| 格式 | doc | ||
| 文件大小 | 832.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-02 21:15:40 | ||
图片预览




文档简介
银川三沙源上游学校2020-2021学年期末考试
高二数学理科试卷
第Ⅰ卷
一、选择题(本大题共12小题,共60)
1.
把28化成二进制数为
A.
B.
C.
D.
2.
命题
“”是命题曲线表示双曲线的(
)
A.
充分不必要条件
B.
充要条件
C.
必要不充分条件
D.
既不充分也不必要条件
3.
如果数据的平均值为,方差为,则的平
均值和方差分别为
A.
和
B.
和
C.
和
D.
和
4.
下列说法中,正确的是(
)
A.
命题“若,则”的逆命题是真命题
B.
命题“或”真命题,则命题“”和命题“”均为真命题
C.
命题“,”的否定是:“,”
D.
已知,则“”是“”的充分不必要条件
5.
一袋中装有3个红球,4个白球,现从中任意取出3个球.记事件为“取出的球都是白球”,事件为“取出的球都是红球”,事件为“取出的球中至少有一个白球”,则下列结论正确的是(
)
A.
与是对立事件
B.
与是互斥事件
C.
与是对立事件
D.
与是互斥事件,但不是对立事件
6.
某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下:
甲
乙
9
8
8
1
7
7
9
9
6
1
0
2
2
5
6
7
9
9
5
3
2
0
3
0
2
3
7
1
0
4
根据上图,对这两名运动员成绩进行比较,下列四个结论中,不正确的是
A.
甲运动员得分的极差大于乙运动员得分的极差
B.
甲运动员得分的的中位数大于乙运动员得分的的中位数
C.
甲运动员的得分平均值大于乙运动员的得分平均值
D.
甲运动员的成绩比乙运动员的成绩稳定
7.
已知抛物线的焦点与椭圆的一个焦点重合,则(
)
A.
B.
C.
D.
8.
某程序框图如图所示,若该程序运行后输出的值是,则
A.
B.
C.
D.
9.
将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到200住在第一营区,从201到500住在第二营区,从501到600住在第三营区,三个营区被抽中的人数依次为(
).
A.
16,26,8
B.
17,24,9
C.
16,25,9
D.
17,25,8
10.
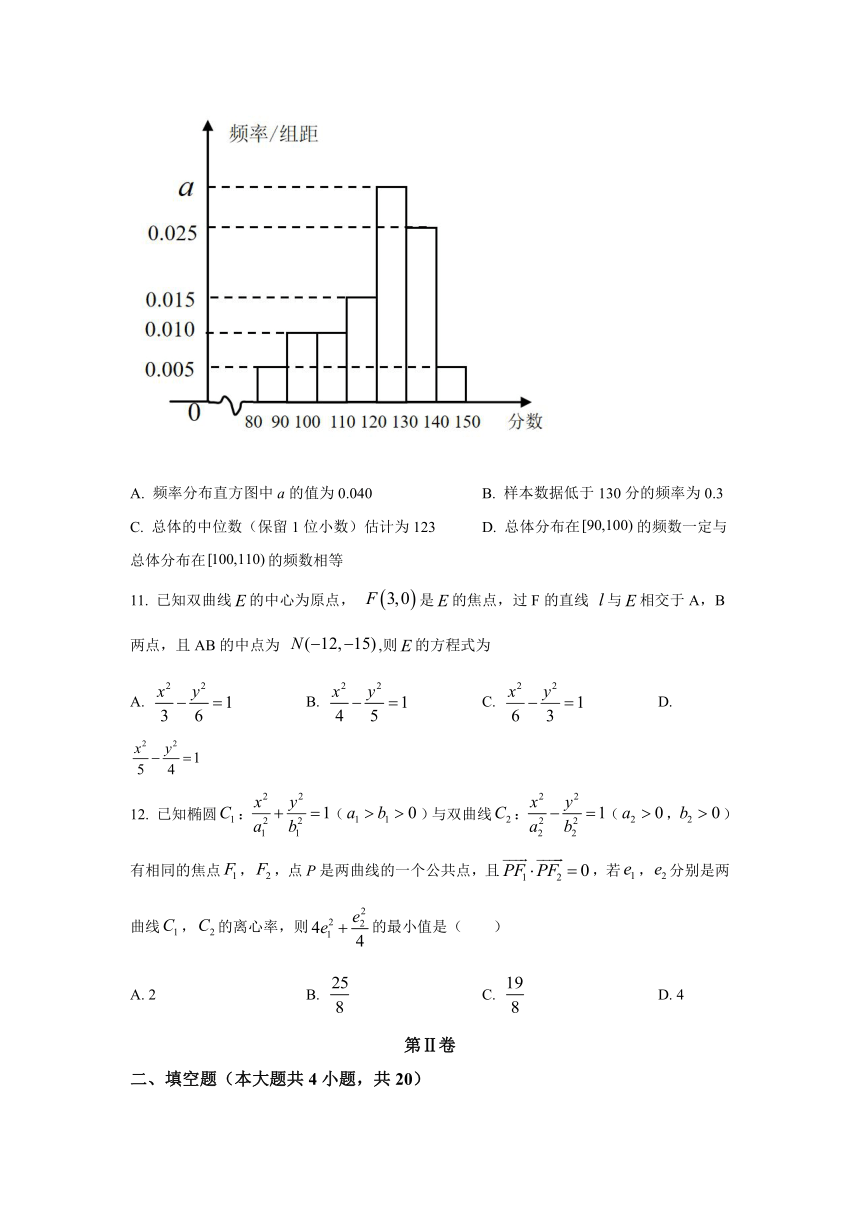
某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在内现将这100名学生的成绩按照,分组后,得到的频率分布直方图如图所示,则下列说法正确的是(
)
A.
频率分布直方图中a的值为0.040
B.
样本数据低于130分的频率为0.3
C.
总体的中位数(保留1位小数)估计为123
D.
总体分布在的频数一定与总体分布在的频数相等
11.
已知双曲线的中心为原点,
是的焦点,过F的直线
与相交于A,B两点,且AB的中点为
,则的方程式为
A.
B.
C.
D.
12.
已知椭圆:()与双曲线:(,)有相同的焦点,,点P是两曲线的一个公共点,且,若,分别是两曲线,的离心率,则的最小值是(
)
A.
2
B.
C.
D.
4
第Ⅱ卷
二、填空题(本大题共4小题,共20)
13.
某工厂生产的30个零件编号为01,02,…,29,30,现利用如下随机数表从中抽取5个进行检测,若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件的编号为__________.
34
57
07
86
36
04
68
96
08
23
23
45
78
89
07
84
42
12
53
31
25
30
07
32
86
32
21
18
34
29
78
64
54
07
32
52
42
06
44
38
12
23
43
56
77
35
78
90
56
42
14.
某公司的班车在8:00准时发车,小田与小方均在7:40至8:00之间到达发车点乘坐班车,且到达发车点的时刻是随机的,则小田比小方至少早5分钟到达发车点的概率为__________.
15.
已知是抛物线上一动点,定点,过点作轴于点,则的最小值是______.
16.
已知双曲线的左、右焦点分别为点,抛物线与双曲线在第一象限内相交于点P,若,则双曲线的离心率为______.
三、解答题(本大题共6小题,共70)
17.
已知:,:,其中.
(1)若且为真,求的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
18.
某地区2007年至2011年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份
2007
2008
2009
2010
2011
年份代号t
1
2
3
4
5
人均纯收入y
3.1
3.6
3.9
44
5
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2011年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
19.
已知圆过,两点,且圆心在上.
(1)求圆的方程;
(2)设点是直线上的动点,,是圆的两条切线,,为切点,求四边形的面积的最小值.
20.
经过多年努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
(1)按分层抽样的方法从质量落在,的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
(2)以各组数据中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:
A.所有黄桃均以20元/千克收购;
B.低于350克的黄桃以5元/个收购,高于或等于350克的以9元/个收购.
请你通过计算为该村选择收益最好的方案.
(参考数据:)
21.
已知点是圆上一动点,作轴,垂足为,且.
(1)求动点的轨迹的方程;
(2)过点斜率为的直线交曲线于,两点,直线,的斜率分别为,,求证:为定值.
22.
在平面直角坐标系中,椭圆的中心为原点,焦点,在轴上,离心率为.过的直线交于,两点,且的周长为.
(1)求椭圆的方程;
(2)圆与轴正半轴相交于两点,(点在点的左侧),过点任作一条直线与椭圆相交于,两点,连接,,求证.
银川三沙源上游学校2020-2021学年期末考试
高二数学理科试卷
答案
第Ⅰ卷
一、选择题(本大题共12小题,共60)
1.
把28化成二进制数为
A.
B.
C.
D.
答案:B
2.
命题
“”是命题曲线表示双曲线的(
)
A.
充分不必要条件
B.
充要条件
C.
必要不充分条件
D.
既不充分也不必要条件
答案:A
3.
如果数据的平均值为,方差为,则的平
均值和方差分别为
A.
和
B.
和
C.
和
D.
和
答案:B
4.
下列说法中,正确的是(
)
A.
命题“若,则”的逆命题是真命题
B.
命题“或”真命题,则命题“”和命题“”均为真命题
C.
命题“,”的否定是:“,”
D.
已知,则“”是“”的充分不必要条件
答案:C
5.
一袋中装有3个红球,4个白球,现从中任意取出3个球.记事件为“取出的球都是白球”,事件为“取出的球都是红球”,事件为“取出的球中至少有一个白球”,则下列结论正确的是(
)
A.
与是对立事件
B.
与是互斥事件
C.
与是对立事件
D.
与是互斥事件,但不是对立事件
答案:A
6.
某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下:
甲
乙
9
8
8
1
7
7
9
9
6
1
0
2
2
5
6
7
9
9
5
3
2
0
3
0
2
3
7
1
0
4
根据上图,对这两名运动员成绩进行比较,下列四个结论中,不正确的是
A.
甲运动员得分的极差大于乙运动员得分的极差
B.
甲运动员得分的的中位数大于乙运动员得分的的中位数
C.
甲运动员的得分平均值大于乙运动员的得分平均值
D.
甲运动员的成绩比乙运动员的成绩稳定
答案:D
7.
已知抛物线的焦点与椭圆的一个焦点重合,则(
)
A.
B.
C.
D.
答案:C
8.
某程序框图如图所示,若该程序运行后输出的值是,则
A.
B.
C.
D.
答案:C
9.
将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到200住在第一营区,从201到500住在第二营区,从501到600住在第三营区,三个营区被抽中的人数依次为(
).
A.
16,26,8
B.
17,24,9
C.
16,25,9
D.
17,25,8
答案:D
10.
某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在内现将这100名学生的成绩按照,分组后,得到的频率分布直方图如图所示,则下列说法正确的是(
)
A.
频率分布直方图中a的值为0.040
B.
样本数据低于130分的频率为0.3
C.
总体的中位数(保留1位小数)估计为123
D.
总体分布在的频数一定与总体分布在的频数相等
答案:C
11.
已知双曲线的中心为原点,
是的焦点,过F的直线
与相交于A,B两点,且AB的中点为
,则的方程式为
A.
B.
C.
D.
答案:B
12.
已知椭圆:()与双曲线:(,)有相同的焦点,,点P是两曲线的一个公共点,且,若,分别是两曲线,的离心率,则的最小值是(
)
A.
2
B.
C.
D.
4
答案:B
第Ⅱ卷
二、填空题(本大题共4小题,共20)
13.
某工厂生产的30个零件编号为01,02,…,29,30,现利用如下随机数表从中抽取5个进行检测,若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件的编号为__________.
34
57
07
86
36
04
68
96
08
23
23
45
78
89
07
84
42
12
53
31
25
30
07
32
86
32
21
18
34
29
78
64
54
07
32
52
42
06
44
38
12
23
43
56
77
35
78
90
56
42
答案:12
14.
某公司的班车在8:00准时发车,小田与小方均在7:40至8:00之间到达发车点乘坐班车,且到达发车点的时刻是随机的,则小田比小方至少早5分钟到达发车点的概率为__________.
答案:
15.
已知是抛物线上一动点,定点,过点作轴于点,则的最小值是______.
答案:
16.
已知双曲线的左、右焦点分别为点,抛物线与双曲线在第一象限内相交于点P,若,则双曲线的离心率为______.
答案:
三、解答题(本大题共6小题,共70)
17.
已知:,:,其中.
(1)若且为真,求的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
答案:(1);(2)
18.
某地区2007年至2011年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份
2007
2008
2009
2010
2011
年份代号t
1
2
3
4
5
人均纯收入y
3.1
3.6
3.9
44
5
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2011年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
答案:(1);(2)2007年至2011年该地区农村居民家庭人均纯收入逐年增加,2015年人均纯收入预测为千元.
19.
已知圆过,两点,且圆心在上.
(1)求圆的方程;
(2)设点是直线上的动点,,是圆的两条切线,,为切点,求四边形的面积的最小值.
答案:(1);(2).
20.
经过多年努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
(1)按分层抽样的方法从质量落在,的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
(2)以各组数据中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:
A.所有黄桃均以20元/千克收购;
B.低于350克的黄桃以5元/个收购,高于或等于350克的以9元/个收购.
请你通过计算为该村选择收益最好的方案.
(参考数据:)
答案:(1)(2)B
21.
已知点是圆上一动点,作轴,垂足为,且.
(1)求动点的轨迹的方程;
(2)过点斜率为的直线交曲线于,两点,直线,的斜率分别为,,求证:为定值.
答案:(1)(2)见解析
22.
在平面直角坐标系中,椭圆的中心为原点,焦点,在轴上,离心率为.过的直线交于,两点,且的周长为.
(1)求椭圆的方程;
(2)圆与轴正半轴相交于两点,(点在点的左侧),过点任作一条直线与椭圆相交于,两点,连接,,求证.
答案:(1);(2)见解析.
高二数学理科试卷
第Ⅰ卷
一、选择题(本大题共12小题,共60)
1.
把28化成二进制数为
A.
B.
C.
D.
2.
命题
“”是命题曲线表示双曲线的(
)
A.
充分不必要条件
B.
充要条件
C.
必要不充分条件
D.
既不充分也不必要条件
3.
如果数据的平均值为,方差为,则的平
均值和方差分别为
A.
和
B.
和
C.
和
D.
和
4.
下列说法中,正确的是(
)
A.
命题“若,则”的逆命题是真命题
B.
命题“或”真命题,则命题“”和命题“”均为真命题
C.
命题“,”的否定是:“,”
D.
已知,则“”是“”的充分不必要条件
5.
一袋中装有3个红球,4个白球,现从中任意取出3个球.记事件为“取出的球都是白球”,事件为“取出的球都是红球”,事件为“取出的球中至少有一个白球”,则下列结论正确的是(
)
A.
与是对立事件
B.
与是互斥事件
C.
与是对立事件
D.
与是互斥事件,但不是对立事件
6.
某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下:
甲
乙
9
8
8
1
7
7
9
9
6
1
0
2
2
5
6
7
9
9
5
3
2
0
3
0
2
3
7
1
0
4
根据上图,对这两名运动员成绩进行比较,下列四个结论中,不正确的是
A.
甲运动员得分的极差大于乙运动员得分的极差
B.
甲运动员得分的的中位数大于乙运动员得分的的中位数
C.
甲运动员的得分平均值大于乙运动员的得分平均值
D.
甲运动员的成绩比乙运动员的成绩稳定
7.
已知抛物线的焦点与椭圆的一个焦点重合,则(
)
A.
B.
C.
D.
8.
某程序框图如图所示,若该程序运行后输出的值是,则
A.
B.
C.
D.
9.
将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到200住在第一营区,从201到500住在第二营区,从501到600住在第三营区,三个营区被抽中的人数依次为(
).
A.
16,26,8
B.
17,24,9
C.
16,25,9
D.
17,25,8
10.
某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在内现将这100名学生的成绩按照,分组后,得到的频率分布直方图如图所示,则下列说法正确的是(
)
A.
频率分布直方图中a的值为0.040
B.
样本数据低于130分的频率为0.3
C.
总体的中位数(保留1位小数)估计为123
D.
总体分布在的频数一定与总体分布在的频数相等
11.
已知双曲线的中心为原点,
是的焦点,过F的直线
与相交于A,B两点,且AB的中点为
,则的方程式为
A.
B.
C.
D.
12.
已知椭圆:()与双曲线:(,)有相同的焦点,,点P是两曲线的一个公共点,且,若,分别是两曲线,的离心率,则的最小值是(
)
A.
2
B.
C.
D.
4
第Ⅱ卷
二、填空题(本大题共4小题,共20)
13.
某工厂生产的30个零件编号为01,02,…,29,30,现利用如下随机数表从中抽取5个进行检测,若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件的编号为__________.
34
57
07
86
36
04
68
96
08
23
23
45
78
89
07
84
42
12
53
31
25
30
07
32
86
32
21
18
34
29
78
64
54
07
32
52
42
06
44
38
12
23
43
56
77
35
78
90
56
42
14.
某公司的班车在8:00准时发车,小田与小方均在7:40至8:00之间到达发车点乘坐班车,且到达发车点的时刻是随机的,则小田比小方至少早5分钟到达发车点的概率为__________.
15.
已知是抛物线上一动点,定点,过点作轴于点,则的最小值是______.
16.
已知双曲线的左、右焦点分别为点,抛物线与双曲线在第一象限内相交于点P,若,则双曲线的离心率为______.
三、解答题(本大题共6小题,共70)
17.
已知:,:,其中.
(1)若且为真,求的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
18.
某地区2007年至2011年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份
2007
2008
2009
2010
2011
年份代号t
1
2
3
4
5
人均纯收入y
3.1
3.6
3.9
44
5
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2011年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
19.
已知圆过,两点,且圆心在上.
(1)求圆的方程;
(2)设点是直线上的动点,,是圆的两条切线,,为切点,求四边形的面积的最小值.
20.
经过多年努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
(1)按分层抽样的方法从质量落在,的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
(2)以各组数据中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:
A.所有黄桃均以20元/千克收购;
B.低于350克的黄桃以5元/个收购,高于或等于350克的以9元/个收购.
请你通过计算为该村选择收益最好的方案.
(参考数据:)
21.
已知点是圆上一动点,作轴,垂足为,且.
(1)求动点的轨迹的方程;
(2)过点斜率为的直线交曲线于,两点,直线,的斜率分别为,,求证:为定值.
22.
在平面直角坐标系中,椭圆的中心为原点,焦点,在轴上,离心率为.过的直线交于,两点,且的周长为.
(1)求椭圆的方程;
(2)圆与轴正半轴相交于两点,(点在点的左侧),过点任作一条直线与椭圆相交于,两点,连接,,求证.
银川三沙源上游学校2020-2021学年期末考试
高二数学理科试卷
答案
第Ⅰ卷
一、选择题(本大题共12小题,共60)
1.
把28化成二进制数为
A.
B.
C.
D.
答案:B
2.
命题
“”是命题曲线表示双曲线的(
)
A.
充分不必要条件
B.
充要条件
C.
必要不充分条件
D.
既不充分也不必要条件
答案:A
3.
如果数据的平均值为,方差为,则的平
均值和方差分别为
A.
和
B.
和
C.
和
D.
和
答案:B
4.
下列说法中,正确的是(
)
A.
命题“若,则”的逆命题是真命题
B.
命题“或”真命题,则命题“”和命题“”均为真命题
C.
命题“,”的否定是:“,”
D.
已知,则“”是“”的充分不必要条件
答案:C
5.
一袋中装有3个红球,4个白球,现从中任意取出3个球.记事件为“取出的球都是白球”,事件为“取出的球都是红球”,事件为“取出的球中至少有一个白球”,则下列结论正确的是(
)
A.
与是对立事件
B.
与是互斥事件
C.
与是对立事件
D.
与是互斥事件,但不是对立事件
答案:A
6.
某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下:
甲
乙
9
8
8
1
7
7
9
9
6
1
0
2
2
5
6
7
9
9
5
3
2
0
3
0
2
3
7
1
0
4
根据上图,对这两名运动员成绩进行比较,下列四个结论中,不正确的是
A.
甲运动员得分的极差大于乙运动员得分的极差
B.
甲运动员得分的的中位数大于乙运动员得分的的中位数
C.
甲运动员的得分平均值大于乙运动员的得分平均值
D.
甲运动员的成绩比乙运动员的成绩稳定
答案:D
7.
已知抛物线的焦点与椭圆的一个焦点重合,则(
)
A.
B.
C.
D.
答案:C
8.
某程序框图如图所示,若该程序运行后输出的值是,则
A.
B.
C.
D.
答案:C
9.
将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到200住在第一营区,从201到500住在第二营区,从501到600住在第三营区,三个营区被抽中的人数依次为(
).
A.
16,26,8
B.
17,24,9
C.
16,25,9
D.
17,25,8
答案:D
10.
某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在内现将这100名学生的成绩按照,分组后,得到的频率分布直方图如图所示,则下列说法正确的是(
)
A.
频率分布直方图中a的值为0.040
B.
样本数据低于130分的频率为0.3
C.
总体的中位数(保留1位小数)估计为123
D.
总体分布在的频数一定与总体分布在的频数相等
答案:C
11.
已知双曲线的中心为原点,
是的焦点,过F的直线
与相交于A,B两点,且AB的中点为
,则的方程式为
A.
B.
C.
D.
答案:B
12.
已知椭圆:()与双曲线:(,)有相同的焦点,,点P是两曲线的一个公共点,且,若,分别是两曲线,的离心率,则的最小值是(
)
A.
2
B.
C.
D.
4
答案:B
第Ⅱ卷
二、填空题(本大题共4小题,共20)
13.
某工厂生产的30个零件编号为01,02,…,29,30,现利用如下随机数表从中抽取5个进行检测,若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件的编号为__________.
34
57
07
86
36
04
68
96
08
23
23
45
78
89
07
84
42
12
53
31
25
30
07
32
86
32
21
18
34
29
78
64
54
07
32
52
42
06
44
38
12
23
43
56
77
35
78
90
56
42
答案:12
14.
某公司的班车在8:00准时发车,小田与小方均在7:40至8:00之间到达发车点乘坐班车,且到达发车点的时刻是随机的,则小田比小方至少早5分钟到达发车点的概率为__________.
答案:
15.
已知是抛物线上一动点,定点,过点作轴于点,则的最小值是______.
答案:
16.
已知双曲线的左、右焦点分别为点,抛物线与双曲线在第一象限内相交于点P,若,则双曲线的离心率为______.
答案:
三、解答题(本大题共6小题,共70)
17.
已知:,:,其中.
(1)若且为真,求的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
答案:(1);(2)
18.
某地区2007年至2011年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份
2007
2008
2009
2010
2011
年份代号t
1
2
3
4
5
人均纯收入y
3.1
3.6
3.9
44
5
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2011年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
答案:(1);(2)2007年至2011年该地区农村居民家庭人均纯收入逐年增加,2015年人均纯收入预测为千元.
19.
已知圆过,两点,且圆心在上.
(1)求圆的方程;
(2)设点是直线上的动点,,是圆的两条切线,,为切点,求四边形的面积的最小值.
答案:(1);(2).
20.
经过多年努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
(1)按分层抽样的方法从质量落在,的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
(2)以各组数据中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:
A.所有黄桃均以20元/千克收购;
B.低于350克的黄桃以5元/个收购,高于或等于350克的以9元/个收购.
请你通过计算为该村选择收益最好的方案.
(参考数据:)
答案:(1)(2)B
21.
已知点是圆上一动点,作轴,垂足为,且.
(1)求动点的轨迹的方程;
(2)过点斜率为的直线交曲线于,两点,直线,的斜率分别为,,求证:为定值.
答案:(1)(2)见解析
22.
在平面直角坐标系中,椭圆的中心为原点,焦点,在轴上,离心率为.过的直线交于,两点,且的周长为.
(1)求椭圆的方程;
(2)圆与轴正半轴相交于两点,(点在点的左侧),过点任作一条直线与椭圆相交于,两点,连接,,求证.
答案:(1);(2)见解析.
同课章节目录
