2021-2022学年苏科版九年级数学上册2.8圆锥的侧面积培优训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册2.8圆锥的侧面积培优训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 13:17:24 | ||
图片预览


文档简介
2.8圆锥的侧面积-2021-2022学年苏科版九年级数学上册
培优训练
一、选择题
1、已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于(
)
A.8
B.4
C.4
D.8
2、有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是( )
A.30π
B.48π
C.60π
D.80π
3、若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为
(
)
A.120°
B.180°
C.240°
D.300°
4、如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是(
)
A.
B.
C.
D.
5、用半径为30cm,圆心角为120 的扇形围成一个圆锥的侧面,则圆锥的底面半径为(
)
A.10
cm
B.30
cm
C.45
cm
D.300
cm
6、圆锥的地面半径为10cm.它的展开图扇形半径为30cm,则这个扇形圆心角的度数是( )
A.60°
B.90°
C.120°
D.150°
7、已知扇形的半径为,圆心角的度数为,若将此扇形围成一个圆锥的侧面,则该圆锥底面圆的周长为(
)
A.
B.
C.
D.
8、如图,从一块直径为4cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.2cm
B.cm
C.2cm
D.1
cm
9、小明用图中所示的扇形纸片作一个圆锥的侧面.已知扇形的半径为5cm,弧长是8πcm,那么这个圆锥的高是( )
A.8cm
B.6cm
C.3cm
D.4cm
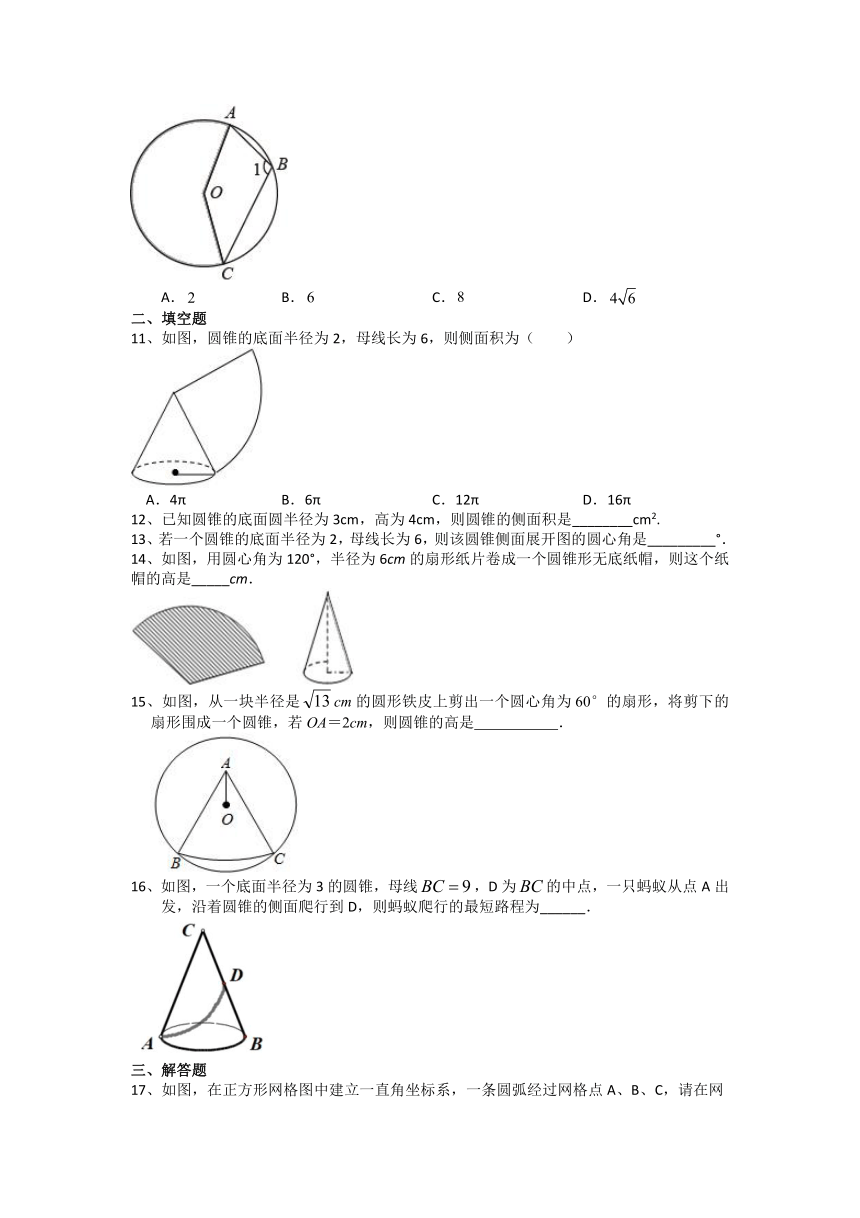
10、如图,点是上的点,已知的半径,欢欢利用图中阴影部分制作一个圆锥,则这个圆锥的高为(
)
A.
B.
C.
D.
二、填空题
11、如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
A.4π
B.6π
C.12π
D.16π
12、已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的侧面积是________cm2.
13、若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是_________°.
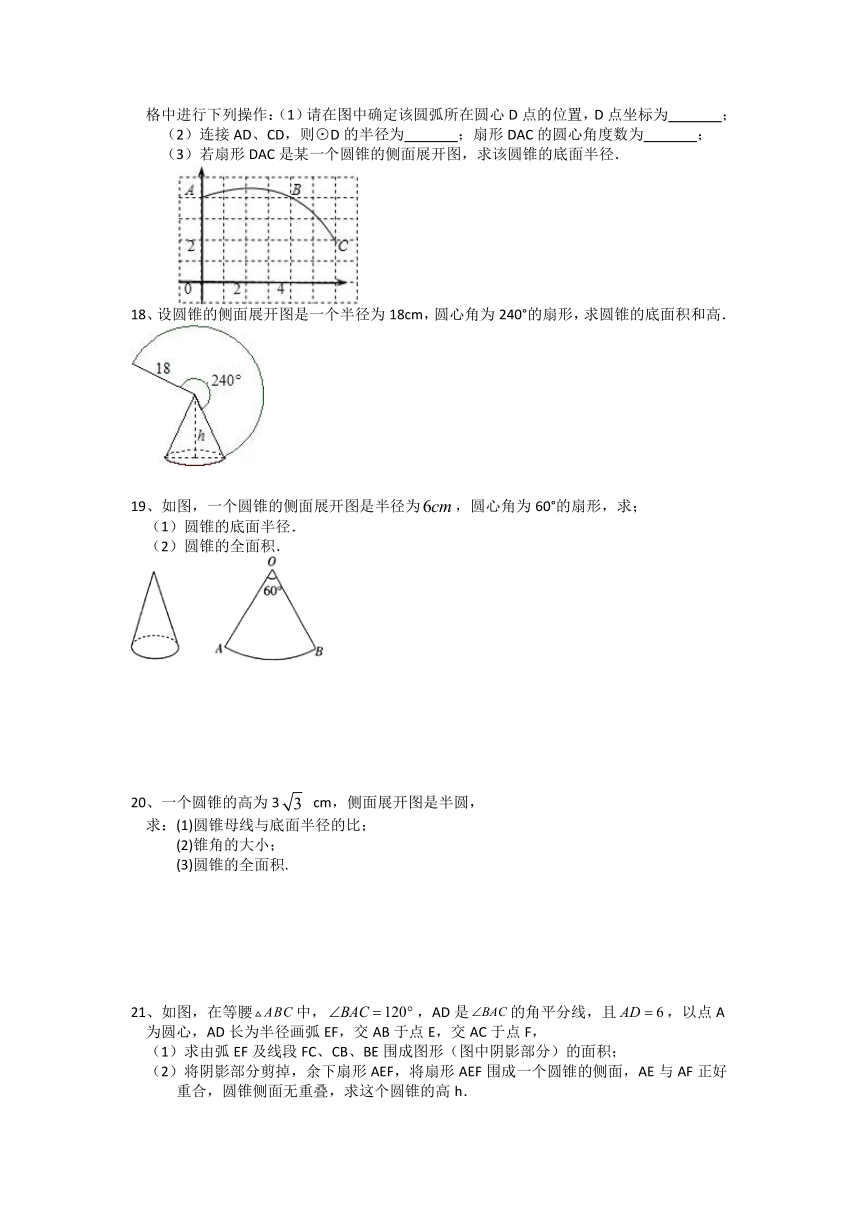
14、如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是_____cm.
15、如图,从一块半径是cm的圆形铁皮上剪出一个圆心角为60°的扇形,将剪下的扇形围成一个圆锥,若OA=2cm,则圆锥的高是
.
16、如图,一个底面半径为3的圆锥,母线,D为的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到D,则蚂蚁爬行的最短路程为______.
三、解答题
17、如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为
;
(2)连接AD、CD,则⊙D的半径为
;扇形DAC的圆心角度数为
;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
18、设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.
19、如图,一个圆锥的侧面展开图是半径为,圆心角为60°的扇形,求;
(1)圆锥的底面半径.
(2)圆锥的全面积.
20、一个圆锥的高为3
cm,侧面展开图是半圆,
求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
21、如图,在等腰中,,AD是的角平分线,且,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F,
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
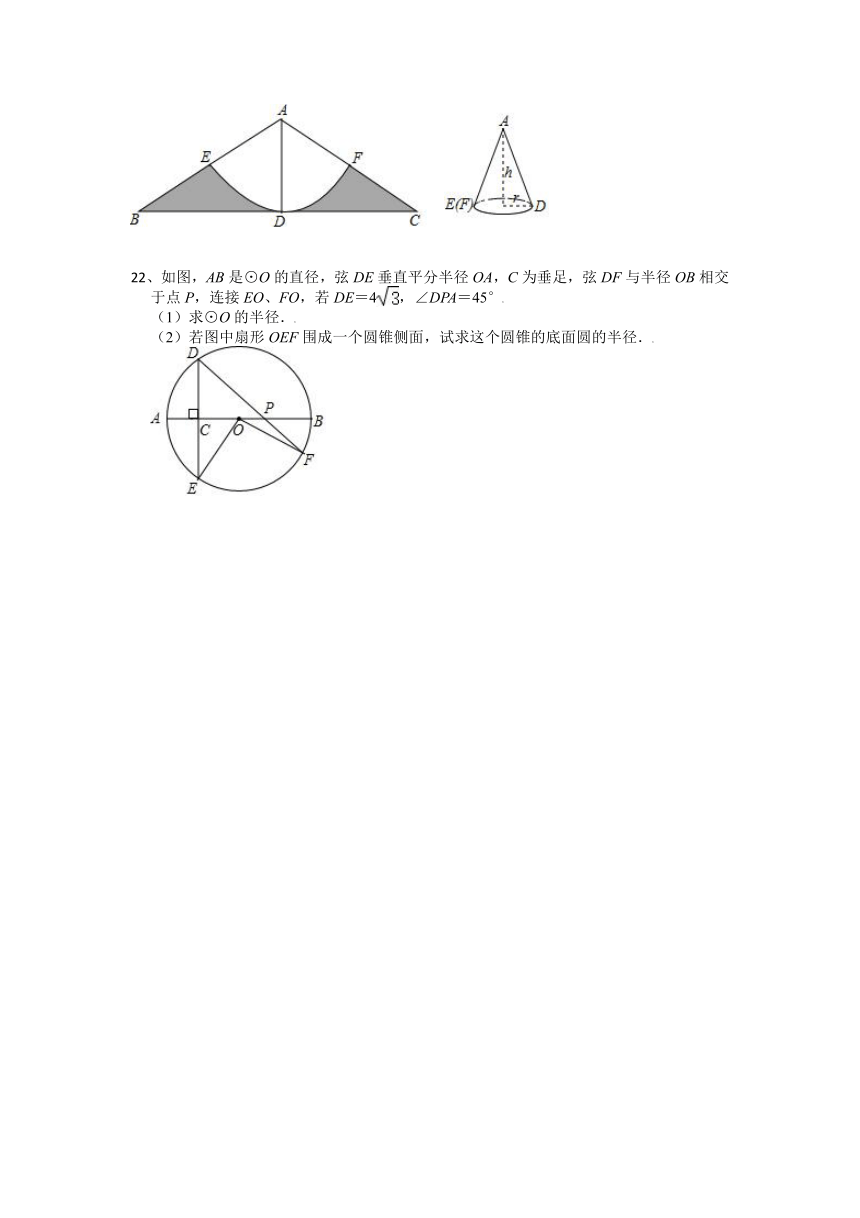
22、如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4,∠DPA=45°
(1)求⊙O的半径.
(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.
2.8圆锥的侧面积-2021-2022学年苏科版九年级数学上册
培优训练(解析)
一、选择题
1、已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于(
)
A.8
B.4
C.4
D.8
【答案】D
【分析】
根据圆锥的侧面积就等于母线长乘底面周长的一半.依此公式计算即可解决问题.
【详解】
解:圆锥的侧面积=π×2×4=8π.
故选:D.
2、有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是( )
A.30π
B.48π
C.60π
D.80π
【思路引导】先根据圆锥的底面半径和高求出母线长,圆锥的侧面积是展开后扇形的面积,计算可得.
【完整解答】解:圆锥的母线==10(cm),
圆锥的底面周长2πr=12π(cm),
圆锥的侧面积=lR=×12π×10=60π(cm2).
故选:C.
3、若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为
(
)
A.120°
B.180°
C.240°
D.300°
【答案】B
【详解】
试题分析:设母线长为R,底面半径为r,
∴底面周长=2πr,底面面积=πr2,侧面面积=πrR,
∵侧面积是底面积的2倍,
∴2πr2=πrR,
∴R=2r,
设圆心角为n,有=2πr=πR,
∴n=180°.
故选B.
4、如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是(
)
A.
B.
C.
D.
【答案】C
【解析】解:∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=5,∴AB边上的高为3×4÷5=2.4,
∴所得几何体的表面积是×2π×2.4×3+×2π×2.4×4=16.8π=.故选:C.
5、用半径为30cm,圆心角为120 的扇形围成一个圆锥的侧面,则圆锥的底面半径为(
)
A.10
cm
B.30
cm
C.45
cm
D.300
cm
【答案】A
【解析】
【分析】设圆锥底面半径为R,根据弧长公式可计算出弧长为20π,把此弧长围成一个圆锥的底面,则根据圆的周长公式得到圆锥底面半径.
【详解】
解:设圆锥底面半径为R,
扇形的弧长=
=20π,
所以20π=2πR,
解得R=10cm,
故本题答案应为:A.
6、圆锥的地面半径为10cm.它的展开图扇形半径为30cm,则这个扇形圆心角的度数是( )
A.60°
B.90°
C.120°
D.150°
【答案】C
【解析】
【分析】根据圆锥的侧面展开图为扇形,圆锥的底面圆的周长等于扇形的弧长得到圆锥的展开图扇形的弧长=2π 10,然后根据扇形的弧长公式l=
计算即可求出n.
【详解】解:设圆锥的展开图扇形的圆心角的度数为.
∵圆锥的底面圆的周长=2π 10=20π,
∴圆锥的展开图扇形的弧长=20π,
∴20π=,
∴n=120°.
故答案选:C.
7、已知扇形的半径为,圆心角的度数为,若将此扇形围成一个圆锥的侧面,则该圆锥底面圆的周长为(
)
A.
B.
C.
D.
【答案】A
【解析】解:设围成的圆锥的底面圆的半径为rcm,
根据题意得2πr=,解得r=2,
则圆锥底面圆的周长为:2πr=4πcm.故选A.
8、如图,从一块直径为4cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.2cm
B.cm
C.2cm
D.1
cm
【答案】D
【解析】∵直径BC=4,∴∠BAC=90°,AB=BC=4,
设这个圆锥的底面圆的半径为r,根据题意得2πr=,解得r=1.
故选D.
9、小明用图中所示的扇形纸片作一个圆锥的侧面.已知扇形的半径为5cm,弧长是8πcm,那么这个圆锥的高是( )
A.8cm
B.6cm
C.3cm
D.4cm
【思路引导】设圆锥底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长得到2πr=8π,解得r=4,然后利用勾股定理计算这个的圆锥的高.
【完整解答】解:设圆锥底面圆的半径为r,
根据题意得2πr=8π,
解得r=4,
所以这个的圆锥的高==3(cm).
故选:C.
10、如图,点是上的点,已知的半径,欢欢利用图中阴影部分制作一个圆锥,则这个圆锥的高为(
)
A.
B.
C.
D.
【答案】C
【分析】根据圆周角定理先求得阴影部分扇形的圆心角度数,再根据弧长公式求得的长,继而求得圆锥的底面半径的长,最后根据勾股定理求得圆锥的高.
【详解】,阴影部分扇形的圆心角,
设圆锥的底面半径为圆锥的高为,
,
故选C
二、填空题
11、如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
A.4π
B.6π
C.12π
D.16π
【答案】C
【解析】根据圆锥的侧面积公式:πrl=π×2×6=12π,
故选C.
12、已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的侧面积是________cm2.
【答案】15π
【分析】设圆锥母线长为l,根据勾股定理求出母线长,再根据圆锥侧面积公式即可得出答案.
【详解】设圆锥母线长为l,∵r=3,h=4,
∴母线l=,
∴S侧=×2πr×5=×2π×3×5=15π,
故答案为15π.
13、若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是_________°.
【答案】120.
【详解】
试题分析:圆锥侧面展开图的弧长是:2π×2=4π(cm),设圆心角的度数是n度.则=4π,解得:n=120.故答案为120.
14、如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是_____cm.
【答案】
【分析】先求出扇形弧长,再求出圆锥的底面半径,再根据勾股定理
即可出圆锥的高.
【详解】
圆心角为120°,半径为6cm的扇形的弧长为4cm
∴圆锥的底面半径为2,
故圆锥的高为=4cm
15、如图,从一块半径是cm的圆形铁皮上剪出一个圆心角为60°的扇形,将剪下的扇形围成一个圆锥,若OA=2cm,则圆锥的高是
.
【思路引导】求出弧BC的长,再求出圆锥底面圆半径,利用勾股定理求出圆锥的高即可.
【完整解答】解:连接OB,过点O作OH⊥AB于H.
由对称性可知,∠OAH=30°,
∵∠AHO=90°,AO=2cm,
∴OH=OA=1(cm),AH=OH=(cm),
∴BH===2(cm),
∴AB=3(cm),
∴的长==π(cm),
设圆锥的底面圆的半径为Rcm,则2πR=π,
∴R=,
∴圆锥的高==(cm).
故答案为:.
16、如图,一个底面半径为3的圆锥,母线,D为的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到D,则蚂蚁爬行的最短路程为______.
【答案】
【解析】画出圆锥侧面展开图如下:
如图,连接AB、AD,设圆锥侧面展开图的圆心角的度数为,
因为圆锥侧面展开图是一个扇形,扇形的弧长等于底面圆的周长,扇形的半径等于母线长,所以,解得,
则,
又,是等边三角形,
点D是BC的中点,,,
在中,,
由两点之间线段最短可知,蚂蚁爬行的最短路程为,
故答案为:.
三、解答题
17、如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为
;
(2)连接AD、CD,则⊙D的半径为
;扇形DAC的圆心角度数为
;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
【答案】(1)(2,0);(2)2,90;(3)
【解析】
(1)如图,分别作AB、BC的垂直平分线,两线交于点D,
∴D点的坐标为(2,0).
(2)连接DA、DC,如图,
则AD=,即⊙D的半径为.
∵OD=CE,OA=DE=4,∠AOD=∠CEO=90°,
∴△AOD≌△DEC,∴∠OAD=∠CDE,
∴∠ADO+∠CDE=∠ADO+∠OAD=90°,∴∠ADC=90°,
即扇形DAC的圆心角度数为90°.
(3)设圆锥的底面半径是r,则,∴,
即该圆锥的底面半径为.
18、设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.
【答案】6.
【分析】
利用弧长公式可得圆锥的侧面展开图的弧长,除以2π即为圆锥的底面半径,圆锥的底面积=π×半径2,圆锥的底面半径,母线长,高构成直角三角形,利用勾股定理即可求得圆锥的高.
【详解】
解:圆锥的弧长为:
∴圆锥的底面半径为24π÷2π=12,
∴圆锥的底面积为π×122=144π,
∴圆锥的高为
19、如图,一个圆锥的侧面展开图是半径为,圆心角为60°的扇形,求;
(1)圆锥的底面半径.
(2)圆锥的全面积.
【答案】(1);(2)
【解析】(1)设圆锥的底面半径为,
扇形的弧长,∴
解得,,即圆锥的底面半径为;
(2)圆锥的全面积.
20、一个圆锥的高为3
cm,侧面展开图是半圆,
求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
【答案】(1)2;(2)60°;(3)27π.
【解析】如图,AO为圆锥的高,经过AO的截面是等腰△ABC,则AB为圆锥母线l,BO为底面半径r.
(1)因圆锥的侧面展开图是半圆,所以2πr=πl,则=2.
(2)因=2,则有AB=2OB,∠BAO=30°,所以∠BAC=60°,即锥角为60°.
(3)因圆锥的母线l,高h和底面半径r构成直角三角形,所以l2=h2+r2;又l=2r,h=3
cm,则r=3
cm,l=6
cm.
所以S表=S侧+S底=πrl+πr2=3·6π+32π=27π(cm2).
21、如图,在等腰中,,AD是的角平分线,且,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F,
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
【答案】(1);(2).
【分析】
(1)利用等腰三角形的性质得到,,则可计算出,然后利用扇形的面积公式,利用由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积进行计算;(2)设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,解得,然后利用勾股定理计算这个圆锥的高h.
【详解】∵在等腰中,,∴,
∵AD是的角平分线,∴,,
∴,∴,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积.
(2)设圆锥的底面圆的半径为r,
根据题意得,解得,
这个圆锥的高.
22、如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4,∠DPA=45°
(1)求⊙O的半径.
(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.
【思路引导】(1)利用垂径定理得到CE=DC=DE=2,OC=OE,则∠OEC=30°,然后利用含30度的直角三角形三边的关系求出OE即可;
(2)利用圆周角定理得到∠EOF=2∠D=90°,设这个圆锥的底面圆的半径为r,利用弧长公式得到2πr=,然后解关于r的方程即可.
【完整解答】解:(1)∵弦DE垂直平分半径OA,
∴CE=DC=DE=2,OC=OE,
∴∠OEC=30°,
∴OC==2,
∴OE=2OC=4,
即⊙O的半径为4;
(2)∵∠DPA=45°,
∴∠D=45°,
∴∠EOF=2∠D=90°,
设这个圆锥的底面圆的半径为r,
∴2πr=,解得r=1,
即这个圆锥的底面圆的半径为1.
培优训练
一、选择题
1、已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于(
)
A.8
B.4
C.4
D.8
2、有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是( )
A.30π
B.48π
C.60π
D.80π
3、若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为
(
)
A.120°
B.180°
C.240°
D.300°
4、如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是(
)
A.
B.
C.
D.
5、用半径为30cm,圆心角为120 的扇形围成一个圆锥的侧面,则圆锥的底面半径为(
)
A.10
cm
B.30
cm
C.45
cm
D.300
cm
6、圆锥的地面半径为10cm.它的展开图扇形半径为30cm,则这个扇形圆心角的度数是( )
A.60°
B.90°
C.120°
D.150°
7、已知扇形的半径为,圆心角的度数为,若将此扇形围成一个圆锥的侧面,则该圆锥底面圆的周长为(
)
A.
B.
C.
D.
8、如图,从一块直径为4cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.2cm
B.cm
C.2cm
D.1
cm
9、小明用图中所示的扇形纸片作一个圆锥的侧面.已知扇形的半径为5cm,弧长是8πcm,那么这个圆锥的高是( )
A.8cm
B.6cm
C.3cm
D.4cm
10、如图,点是上的点,已知的半径,欢欢利用图中阴影部分制作一个圆锥,则这个圆锥的高为(
)
A.
B.
C.
D.
二、填空题
11、如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
A.4π
B.6π
C.12π
D.16π
12、已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的侧面积是________cm2.
13、若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是_________°.
14、如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是_____cm.
15、如图,从一块半径是cm的圆形铁皮上剪出一个圆心角为60°的扇形,将剪下的扇形围成一个圆锥,若OA=2cm,则圆锥的高是
.
16、如图,一个底面半径为3的圆锥,母线,D为的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到D,则蚂蚁爬行的最短路程为______.
三、解答题
17、如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为
;
(2)连接AD、CD,则⊙D的半径为
;扇形DAC的圆心角度数为
;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
18、设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.
19、如图,一个圆锥的侧面展开图是半径为,圆心角为60°的扇形,求;
(1)圆锥的底面半径.
(2)圆锥的全面积.
20、一个圆锥的高为3
cm,侧面展开图是半圆,
求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
21、如图,在等腰中,,AD是的角平分线,且,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F,
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
22、如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4,∠DPA=45°
(1)求⊙O的半径.
(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.
2.8圆锥的侧面积-2021-2022学年苏科版九年级数学上册
培优训练(解析)
一、选择题
1、已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于(
)
A.8
B.4
C.4
D.8
【答案】D
【分析】
根据圆锥的侧面积就等于母线长乘底面周长的一半.依此公式计算即可解决问题.
【详解】
解:圆锥的侧面积=π×2×4=8π.
故选:D.
2、有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是( )
A.30π
B.48π
C.60π
D.80π
【思路引导】先根据圆锥的底面半径和高求出母线长,圆锥的侧面积是展开后扇形的面积,计算可得.
【完整解答】解:圆锥的母线==10(cm),
圆锥的底面周长2πr=12π(cm),
圆锥的侧面积=lR=×12π×10=60π(cm2).
故选:C.
3、若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为
(
)
A.120°
B.180°
C.240°
D.300°
【答案】B
【详解】
试题分析:设母线长为R,底面半径为r,
∴底面周长=2πr,底面面积=πr2,侧面面积=πrR,
∵侧面积是底面积的2倍,
∴2πr2=πrR,
∴R=2r,
设圆心角为n,有=2πr=πR,
∴n=180°.
故选B.
4、如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是(
)
A.
B.
C.
D.
【答案】C
【解析】解:∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=5,∴AB边上的高为3×4÷5=2.4,
∴所得几何体的表面积是×2π×2.4×3+×2π×2.4×4=16.8π=.故选:C.
5、用半径为30cm,圆心角为120 的扇形围成一个圆锥的侧面,则圆锥的底面半径为(
)
A.10
cm
B.30
cm
C.45
cm
D.300
cm
【答案】A
【解析】
【分析】设圆锥底面半径为R,根据弧长公式可计算出弧长为20π,把此弧长围成一个圆锥的底面,则根据圆的周长公式得到圆锥底面半径.
【详解】
解:设圆锥底面半径为R,
扇形的弧长=
=20π,
所以20π=2πR,
解得R=10cm,
故本题答案应为:A.
6、圆锥的地面半径为10cm.它的展开图扇形半径为30cm,则这个扇形圆心角的度数是( )
A.60°
B.90°
C.120°
D.150°
【答案】C
【解析】
【分析】根据圆锥的侧面展开图为扇形,圆锥的底面圆的周长等于扇形的弧长得到圆锥的展开图扇形的弧长=2π 10,然后根据扇形的弧长公式l=
计算即可求出n.
【详解】解:设圆锥的展开图扇形的圆心角的度数为.
∵圆锥的底面圆的周长=2π 10=20π,
∴圆锥的展开图扇形的弧长=20π,
∴20π=,
∴n=120°.
故答案选:C.
7、已知扇形的半径为,圆心角的度数为,若将此扇形围成一个圆锥的侧面,则该圆锥底面圆的周长为(
)
A.
B.
C.
D.
【答案】A
【解析】解:设围成的圆锥的底面圆的半径为rcm,
根据题意得2πr=,解得r=2,
则圆锥底面圆的周长为:2πr=4πcm.故选A.
8、如图,从一块直径为4cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.2cm
B.cm
C.2cm
D.1
cm
【答案】D
【解析】∵直径BC=4,∴∠BAC=90°,AB=BC=4,
设这个圆锥的底面圆的半径为r,根据题意得2πr=,解得r=1.
故选D.
9、小明用图中所示的扇形纸片作一个圆锥的侧面.已知扇形的半径为5cm,弧长是8πcm,那么这个圆锥的高是( )
A.8cm
B.6cm
C.3cm
D.4cm
【思路引导】设圆锥底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长得到2πr=8π,解得r=4,然后利用勾股定理计算这个的圆锥的高.
【完整解答】解:设圆锥底面圆的半径为r,
根据题意得2πr=8π,
解得r=4,
所以这个的圆锥的高==3(cm).
故选:C.
10、如图,点是上的点,已知的半径,欢欢利用图中阴影部分制作一个圆锥,则这个圆锥的高为(
)
A.
B.
C.
D.
【答案】C
【分析】根据圆周角定理先求得阴影部分扇形的圆心角度数,再根据弧长公式求得的长,继而求得圆锥的底面半径的长,最后根据勾股定理求得圆锥的高.
【详解】,阴影部分扇形的圆心角,
设圆锥的底面半径为圆锥的高为,
,
故选C
二、填空题
11、如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
A.4π
B.6π
C.12π
D.16π
【答案】C
【解析】根据圆锥的侧面积公式:πrl=π×2×6=12π,
故选C.
12、已知圆锥的底面圆半径为3cm,高为4cm,则圆锥的侧面积是________cm2.
【答案】15π
【分析】设圆锥母线长为l,根据勾股定理求出母线长,再根据圆锥侧面积公式即可得出答案.
【详解】设圆锥母线长为l,∵r=3,h=4,
∴母线l=,
∴S侧=×2πr×5=×2π×3×5=15π,
故答案为15π.
13、若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是_________°.
【答案】120.
【详解】
试题分析:圆锥侧面展开图的弧长是:2π×2=4π(cm),设圆心角的度数是n度.则=4π,解得:n=120.故答案为120.
14、如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是_____cm.
【答案】
【分析】先求出扇形弧长,再求出圆锥的底面半径,再根据勾股定理
即可出圆锥的高.
【详解】
圆心角为120°,半径为6cm的扇形的弧长为4cm
∴圆锥的底面半径为2,
故圆锥的高为=4cm
15、如图,从一块半径是cm的圆形铁皮上剪出一个圆心角为60°的扇形,将剪下的扇形围成一个圆锥,若OA=2cm,则圆锥的高是
.
【思路引导】求出弧BC的长,再求出圆锥底面圆半径,利用勾股定理求出圆锥的高即可.
【完整解答】解:连接OB,过点O作OH⊥AB于H.
由对称性可知,∠OAH=30°,
∵∠AHO=90°,AO=2cm,
∴OH=OA=1(cm),AH=OH=(cm),
∴BH===2(cm),
∴AB=3(cm),
∴的长==π(cm),
设圆锥的底面圆的半径为Rcm,则2πR=π,
∴R=,
∴圆锥的高==(cm).
故答案为:.
16、如图,一个底面半径为3的圆锥,母线,D为的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到D,则蚂蚁爬行的最短路程为______.
【答案】
【解析】画出圆锥侧面展开图如下:
如图,连接AB、AD,设圆锥侧面展开图的圆心角的度数为,
因为圆锥侧面展开图是一个扇形,扇形的弧长等于底面圆的周长,扇形的半径等于母线长,所以,解得,
则,
又,是等边三角形,
点D是BC的中点,,,
在中,,
由两点之间线段最短可知,蚂蚁爬行的最短路程为,
故答案为:.
三、解答题
17、如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为
;
(2)连接AD、CD,则⊙D的半径为
;扇形DAC的圆心角度数为
;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
【答案】(1)(2,0);(2)2,90;(3)
【解析】
(1)如图,分别作AB、BC的垂直平分线,两线交于点D,
∴D点的坐标为(2,0).
(2)连接DA、DC,如图,
则AD=,即⊙D的半径为.
∵OD=CE,OA=DE=4,∠AOD=∠CEO=90°,
∴△AOD≌△DEC,∴∠OAD=∠CDE,
∴∠ADO+∠CDE=∠ADO+∠OAD=90°,∴∠ADC=90°,
即扇形DAC的圆心角度数为90°.
(3)设圆锥的底面半径是r,则,∴,
即该圆锥的底面半径为.
18、设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.
【答案】6.
【分析】
利用弧长公式可得圆锥的侧面展开图的弧长,除以2π即为圆锥的底面半径,圆锥的底面积=π×半径2,圆锥的底面半径,母线长,高构成直角三角形,利用勾股定理即可求得圆锥的高.
【详解】
解:圆锥的弧长为:
∴圆锥的底面半径为24π÷2π=12,
∴圆锥的底面积为π×122=144π,
∴圆锥的高为
19、如图,一个圆锥的侧面展开图是半径为,圆心角为60°的扇形,求;
(1)圆锥的底面半径.
(2)圆锥的全面积.
【答案】(1);(2)
【解析】(1)设圆锥的底面半径为,
扇形的弧长,∴
解得,,即圆锥的底面半径为;
(2)圆锥的全面积.
20、一个圆锥的高为3
cm,侧面展开图是半圆,
求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
【答案】(1)2;(2)60°;(3)27π.
【解析】如图,AO为圆锥的高,经过AO的截面是等腰△ABC,则AB为圆锥母线l,BO为底面半径r.
(1)因圆锥的侧面展开图是半圆,所以2πr=πl,则=2.
(2)因=2,则有AB=2OB,∠BAO=30°,所以∠BAC=60°,即锥角为60°.
(3)因圆锥的母线l,高h和底面半径r构成直角三角形,所以l2=h2+r2;又l=2r,h=3
cm,则r=3
cm,l=6
cm.
所以S表=S侧+S底=πrl+πr2=3·6π+32π=27π(cm2).
21、如图,在等腰中,,AD是的角平分线,且,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F,
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
【答案】(1);(2).
【分析】
(1)利用等腰三角形的性质得到,,则可计算出,然后利用扇形的面积公式,利用由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积进行计算;(2)设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,解得,然后利用勾股定理计算这个圆锥的高h.
【详解】∵在等腰中,,∴,
∵AD是的角平分线,∴,,
∴,∴,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积.
(2)设圆锥的底面圆的半径为r,
根据题意得,解得,
这个圆锥的高.
22、如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4,∠DPA=45°
(1)求⊙O的半径.
(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.
【思路引导】(1)利用垂径定理得到CE=DC=DE=2,OC=OE,则∠OEC=30°,然后利用含30度的直角三角形三边的关系求出OE即可;
(2)利用圆周角定理得到∠EOF=2∠D=90°,设这个圆锥的底面圆的半径为r,利用弧长公式得到2πr=,然后解关于r的方程即可.
【完整解答】解:(1)∵弦DE垂直平分半径OA,
∴CE=DC=DE=2,OC=OE,
∴∠OEC=30°,
∴OC==2,
∴OE=2OC=4,
即⊙O的半径为4;
(2)∵∠DPA=45°,
∴∠D=45°,
∴∠EOF=2∠D=90°,
设这个圆锥的底面圆的半径为r,
∴2πr=,解得r=1,
即这个圆锥的底面圆的半径为1.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
