沪教版(上海)高中数学高一下册 4.6 对数函数 课件4(共35张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 4.6 对数函数 课件4(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:31:37 | ||
图片预览











文档简介
(共35张PPT)
对数与对数函数
1.对数的概念及运算性质
(1)对数的概念
如果ab=N(a>0,a≠1),那么b叫做以a为底N的对数,记
.
以10为底的对数叫做常用对数,记作
.以无理数e=2.71828…为底的对数叫做自然对数,记作
.
(2)对数的性质
①
没有对数;②loga1=
;③logaa=
;④alogaN=N(对数恒等式).
lgN
lnN
零与负数
0
1
logaN=b(a>0,a≠1)
logaM+logaN
logaM-logaN
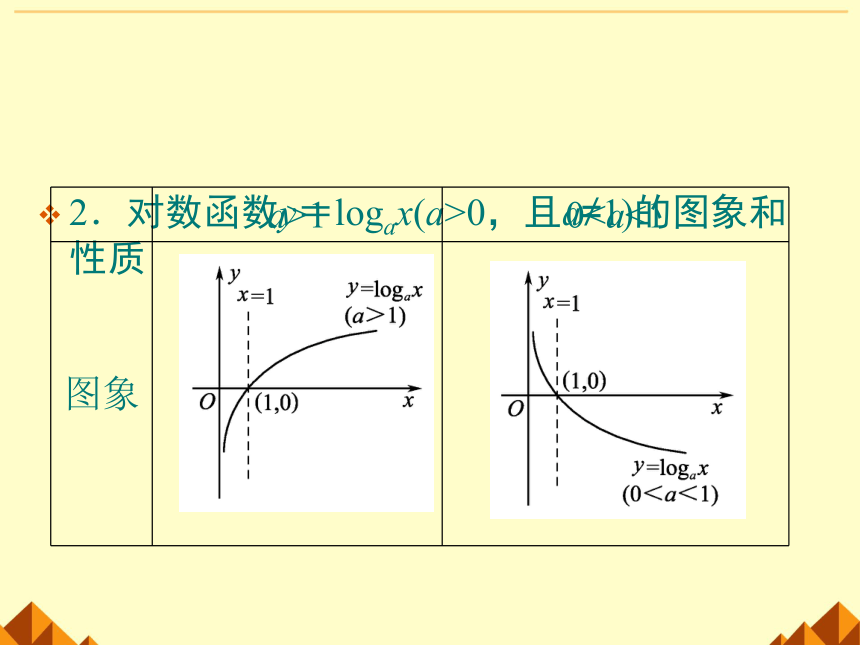
2.对数函数y=logax(a>0,且a≠1)的图象和性质
a>1
0图象
a>1
0性质
(1)定义域:
(1)定义域:
(2)值域:
(2)值域:
(3)过点
,即
(3)过点
,即
(4)当x>1时,
当0(4)当x>1时,
当0(5)是(0,+∞)上的
函数
(5)是(0,+∞)上的
函数
(0,+∞)
(0,+∞)
R
R
(1,0)
x=1时,y=0
(1,0)
x=1时,y=0
y>0
y<0
y<0
y>0
减
增
3.指数函数y=ax与对数函数y=logax互为反函数(a>0且a≠1)其图象关于直线y=x对称.
[答案] D
2.(2011·佛山一模)已知函数f(x)为奇函数,且当x>0时,f(x)=log2x.则满足不等式f(x)>0的x的取值范围是________.
[答案] (-1,0)∪(1,+∞)
3.(2010·天津文数)设a=log54,b=(log53)2,c=log45,则( )
A.a<c<b
B.b<c<a
C.a<b<c
D.b<a<c
[解析] 因为0<log53<1,所以0<(log53)2<log53,又log53<log54<1 log45>1,所以b<a<c.
[答案] D
[分析] 本题主要考查对数的基础知识以及恒等变
形的能力.
[点评与警示] 解决含多个对数式的求值化简问题,关键是熟练掌握对数的运算性质,不但要能正用、逆用这些公式,还要会变式应用,创造条件去应用.
[答案] A
[分析] 由于两组数都不是同一个函数的函数值,难以用一个函数单调性作出判断,应依据函数的性质,采用间接比较的方法.
[点评与警示]①
函数的单调性揭示了自变量的大小与函数值大小的相互转换关系;②当不能用一个函数的单调性作出判断时,应通过引入第三个过渡量(如0,1等)搭桥,进而求解.
设a=log0.70.8,b=log1.10.9,c=1.10.9,则a、b、c的大小顺序是( )
A.aB.bC.bD.c[解析] 因为01.10=1,所以选C.
[答案] C
[点评与警示] 对数函数图象的分布规律为:位于第一象
限的部分,随着底数的由小到大,图象从左到右分布.
如右图,三个对数函数的图象,若ax1=bx2=cx3>1,则x1,x2,x3的大小关系是( )
A.x1>x2>x3
B.x3>x2>x1
C.x3>x1>x2
D.x2>x1>x3
[解析] 由图可知a>1>c>b>0,作曲线c1:y=ax,c2:y=bx,c3:y=cx,并作y=2,与曲线交点坐标A(x1,2),B(x2,2),C(x3,2),知x1>x2>x3,故选A.
[答案] A
(2010·全国Ⅰ,7)已知函数f(x)=|lgx|.若a≠b,且f(a)=f(b),则a+b的取值范围是( )
A.(1,+∞)
B.[1,+∞)
C.(2,+∞)
D.[2,+∞)
设0A.(-∞,0)
B.(0,+∞)
C.(-∞,loga3)
D.(loga3,+∞)
[解析] ∵0∴由f(x)<0可得:a2x-2ax-2>1,即(ax-3)(ax+1)>0.
∴ax>3,∴x[答案] C
[点评与警示] (1)要判断函数的单调性,必须首先确定其定义域,特别是对数函数,切记真数大于零,以免产生错解;(2)注意分类讨论与灵活运用复合函数的单调性.
[分析] (1)将问题转化为求不等式的解集为全体实数时的参数的取值问题;(2)将问题转化为使函数u=x2-2ax+3的值域为R+时的参数取值问题;(3)将问题转化为求使u=x2-2ax+3>0对x∈[-1,+∞)上恒成立的参数取值;(4)命题等价于x2-2ax+3>0的解集为{x|x<1或x>3}.
(4)命题等价于x2-2ax+3>0的解集为{x|x<1或x>3}
∴x2-2ax+3=0的两根为1和3,
∴2a=1+3即a=2
[点评与警示] 对数函数的值域为R时,其真数必须取遍所有的正数.
2.对数函数的单调性受到底数a大小变化的影响,因此解题时常对底数a按0<a<1和a>1进行分类讨论.
3.形如y=logaf(x)(a>0,a≠1)的函数有如下性质
(1)定义域是函数u=f(x)定义域与不等式f(x)>0的解集的交集M;
(2)求值域时,先确定函数u=f(x)(x∈M)的值域,然后以u的值域作为函数y=logau(a>0,a≠1)的定义域,从而求得函数y=logaf(x)(a>0,a≠1)的值域.
4.对数值的大小比较的方法.
(1)化同底后利用函数的单调性;
(2)作差或作商法;
(3)利用中间量(0或1);
(4)化同真数后利用图象比较.
5.“当底数与真数同时大于1或底数与真数同时大于0而小于1时,对数值是正数,否则对数值小于0”.这一结论对解选择题,填空题很有帮助,能大大提高解题的效率.
对数与对数函数
1.对数的概念及运算性质
(1)对数的概念
如果ab=N(a>0,a≠1),那么b叫做以a为底N的对数,记
.
以10为底的对数叫做常用对数,记作
.以无理数e=2.71828…为底的对数叫做自然对数,记作
.
(2)对数的性质
①
没有对数;②loga1=
;③logaa=
;④alogaN=N(对数恒等式).
lgN
lnN
零与负数
0
1
logaN=b(a>0,a≠1)
logaM+logaN
logaM-logaN
2.对数函数y=logax(a>0,且a≠1)的图象和性质
a>1
0
a>1
0
(1)定义域:
(1)定义域:
(2)值域:
(2)值域:
(3)过点
,即
(3)过点
,即
(4)当x>1时,
当0
当0
函数
(5)是(0,+∞)上的
函数
(0,+∞)
(0,+∞)
R
R
(1,0)
x=1时,y=0
(1,0)
x=1时,y=0
y>0
y<0
y<0
y>0
减
增
3.指数函数y=ax与对数函数y=logax互为反函数(a>0且a≠1)其图象关于直线y=x对称.
[答案] D
2.(2011·佛山一模)已知函数f(x)为奇函数,且当x>0时,f(x)=log2x.则满足不等式f(x)>0的x的取值范围是________.
[答案] (-1,0)∪(1,+∞)
3.(2010·天津文数)设a=log54,b=(log53)2,c=log45,则( )
A.a<c<b
B.b<c<a
C.a<b<c
D.b<a<c
[解析] 因为0<log53<1,所以0<(log53)2<log53,又log53<log54<1 log45>1,所以b<a<c.
[答案] D
[分析] 本题主要考查对数的基础知识以及恒等变
形的能力.
[点评与警示] 解决含多个对数式的求值化简问题,关键是熟练掌握对数的运算性质,不但要能正用、逆用这些公式,还要会变式应用,创造条件去应用.
[答案] A
[分析] 由于两组数都不是同一个函数的函数值,难以用一个函数单调性作出判断,应依据函数的性质,采用间接比较的方法.
[点评与警示]①
函数的单调性揭示了自变量的大小与函数值大小的相互转换关系;②当不能用一个函数的单调性作出判断时,应通过引入第三个过渡量(如0,1等)搭桥,进而求解.
设a=log0.70.8,b=log1.10.9,c=1.10.9,则a、b、c的大小顺序是( )
A.a
[答案] C
[点评与警示] 对数函数图象的分布规律为:位于第一象
限的部分,随着底数的由小到大,图象从左到右分布.
如右图,三个对数函数的图象,若ax1=bx2=cx3>1,则x1,x2,x3的大小关系是( )
A.x1>x2>x3
B.x3>x2>x1
C.x3>x1>x2
D.x2>x1>x3
[解析] 由图可知a>1>c>b>0,作曲线c1:y=ax,c2:y=bx,c3:y=cx,并作y=2,与曲线交点坐标A(x1,2),B(x2,2),C(x3,2),知x1>x2>x3,故选A.
[答案] A
(2010·全国Ⅰ,7)已知函数f(x)=|lgx|.若a≠b,且f(a)=f(b),则a+b的取值范围是( )
A.(1,+∞)
B.[1,+∞)
C.(2,+∞)
D.[2,+∞)
设0
B.(0,+∞)
C.(-∞,loga3)
D.(loga3,+∞)
[解析] ∵0
∴ax>3,∴x
[点评与警示] (1)要判断函数的单调性,必须首先确定其定义域,特别是对数函数,切记真数大于零,以免产生错解;(2)注意分类讨论与灵活运用复合函数的单调性.
[分析] (1)将问题转化为求不等式的解集为全体实数时的参数的取值问题;(2)将问题转化为使函数u=x2-2ax+3的值域为R+时的参数取值问题;(3)将问题转化为求使u=x2-2ax+3>0对x∈[-1,+∞)上恒成立的参数取值;(4)命题等价于x2-2ax+3>0的解集为{x|x<1或x>3}.
(4)命题等价于x2-2ax+3>0的解集为{x|x<1或x>3}
∴x2-2ax+3=0的两根为1和3,
∴2a=1+3即a=2
[点评与警示] 对数函数的值域为R时,其真数必须取遍所有的正数.
2.对数函数的单调性受到底数a大小变化的影响,因此解题时常对底数a按0<a<1和a>1进行分类讨论.
3.形如y=logaf(x)(a>0,a≠1)的函数有如下性质
(1)定义域是函数u=f(x)定义域与不等式f(x)>0的解集的交集M;
(2)求值域时,先确定函数u=f(x)(x∈M)的值域,然后以u的值域作为函数y=logau(a>0,a≠1)的定义域,从而求得函数y=logaf(x)(a>0,a≠1)的值域.
4.对数值的大小比较的方法.
(1)化同底后利用函数的单调性;
(2)作差或作商法;
(3)利用中间量(0或1);
(4)化同真数后利用图象比较.
5.“当底数与真数同时大于1或底数与真数同时大于0而小于1时,对数值是正数,否则对数值小于0”.这一结论对解选择题,填空题很有帮助,能大大提高解题的效率.
