沪教版(上海)高中数学高一下册 4.6 对数函数 课件32(共20张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 4.6 对数函数 课件32(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 946.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
对数函数及其性质(一)
1.一般地,我们把函数
y=logax(a>0,且
a≠1)叫做对数函
数,其中___是自变量,函数的定义域是__________,值域是实
数集
R.
x
(0,+∞)
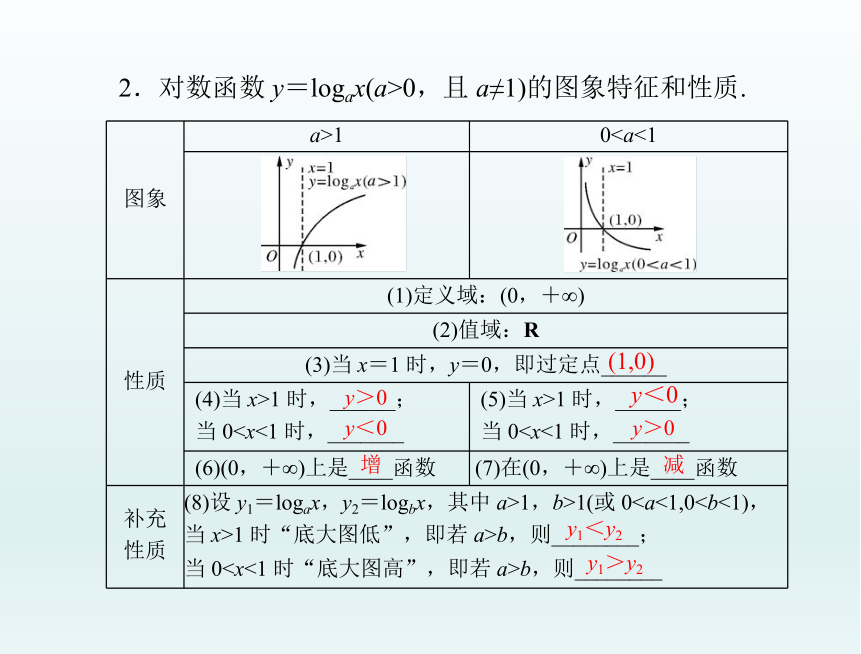
图象
a>1
0性质
(1)定义域:(0,+∞)
(2)值域:R
(3)当
x=1
时,y=0,即过定点______
(4)当
x>1
时,______;
当
0时,_______
(5)当
x>1
时,______;
当
0时,_______
(6)(0,+∞)上是____函数
(7)在(0,+∞)上是____函数
补充
性质
(8)设
y1=logax,y2=logbx,其中
a>1,b>1(或
0当
x>1
时“底大图低”,即若
a>b,则________;
当
0时“底大图高”,即若
a>b,则________
2.对数函数
y=logax(a>0,且
a≠1)的图象特征和性质.
y>0
y<0
y>0
增
减
y1<y2
y1>y2
(1,0)
y<0
重点
对数函数的概念
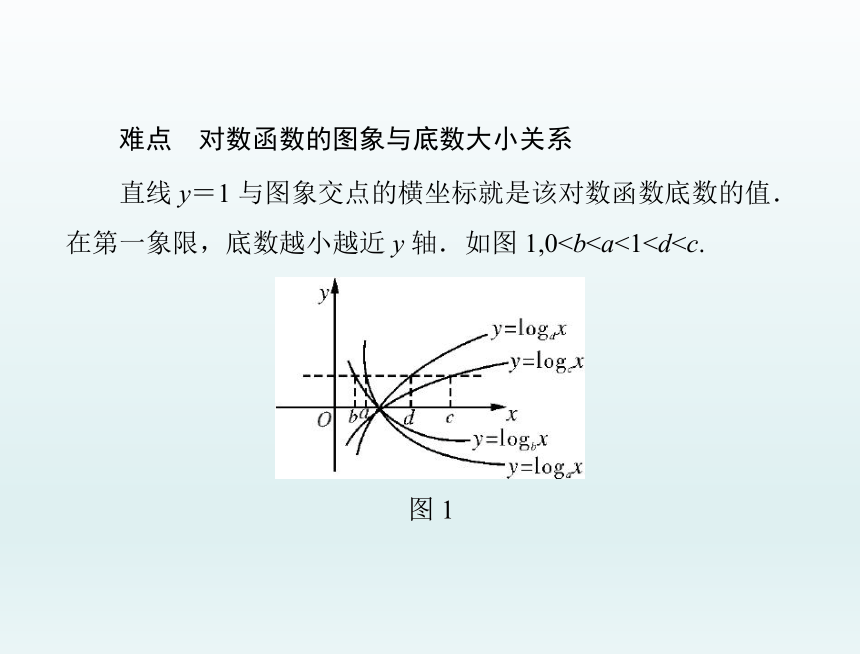
难点
对数函数的图象与底数大小关系
直线
y=1
与图象交点的横坐标就是该对数函数底数的值.
在第一象限,底数越小越近
y
轴.如图
1,0图
1
求函数的定义域、值域
思维突破:定义域即是使函数解析式有意义的
x
的取值范
围.
求与对数函数有关的函数定义域时,除满足
函数定义域外,对这种函数自身还有如下要求:一是要特别注意
真数大于零;二是要注意底数;三是按底数的取值应用单调性.
1-1.求下列函数的定义域:
1-2.求下列函数的值域:
函数图象问题
例
2:作函数
y=|log2(x+1)|+2
的图象.
思维突破:由
y=log2x
的图象,通过平移、对称变换得到
y=|log2(x+1)|+2
的图象.
图
2
图
2
一般地,要得到
y=f(x+a)+b
的图象,可
把
y=f(x)沿
x
轴向右(a<0)或向左(a>0)平移|a|个单位,再沿
y
轴
方向向上(b>0)或向下(b<0)平移|b|个单位.而要得到
y=|f(x)|的
图象,则可对
y=f(x)在
x
轴下方的图象作关于
x
轴的对称变换,
同时保留其在
x
轴上方的图象.
C
利用函数性质比较大小
例
3:比较下列三组数的大小关系:
思维突破:若同底,则利用相应函数单调性解决;不同底,
可考虑化同底或与
1,0
比大小,或借助图象观察得到结论.
利用对数函数的单调性进行对数值的大小
比较,常用的方法如下:①若底数为同一常数,则可由对数函
数的单调性直接判断;②若底数为同一字母,则按对数函数的
单调性对底数进行分类讨论;③若底数不同,真数相同,则可
用换底公式化为同底,再进行比较;④若底数、真数都不相同,
则常借助
1,0,-1
等中间量进行比较或利用对数函数图象的性
质进行判断.
3-1.已知
loga3>logb3,试比较
a
与
b
的大小.
例
4:设函数
y=f(x),且
lg(lgy)=lg3x+lg(3-x),求:
(1)f(x)的表达式及定义域;
(2)f(x)的值域.
错因剖析:没有考虑所给式子的限制,所求函数的定义域
必须使原式有意义,不能仅根据对数符号所得的解析式去确定
函数的定义域.
对数函数及其性质(一)
1.一般地,我们把函数
y=logax(a>0,且
a≠1)叫做对数函
数,其中___是自变量,函数的定义域是__________,值域是实
数集
R.
x
(0,+∞)
图象
a>1
0
(1)定义域:(0,+∞)
(2)值域:R
(3)当
x=1
时,y=0,即过定点______
(4)当
x>1
时,______;
当
0
(5)当
x>1
时,______;
当
0
(6)(0,+∞)上是____函数
(7)在(0,+∞)上是____函数
补充
性质
(8)设
y1=logax,y2=logbx,其中
a>1,b>1(或
0
x>1
时“底大图低”,即若
a>b,则________;
当
0
a>b,则________
2.对数函数
y=logax(a>0,且
a≠1)的图象特征和性质.
y>0
y<0
y>0
增
减
y1<y2
y1>y2
(1,0)
y<0
重点
对数函数的概念
难点
对数函数的图象与底数大小关系
直线
y=1
与图象交点的横坐标就是该对数函数底数的值.
在第一象限,底数越小越近
y
轴.如图
1,0
1
求函数的定义域、值域
思维突破:定义域即是使函数解析式有意义的
x
的取值范
围.
求与对数函数有关的函数定义域时,除满足
函数定义域外,对这种函数自身还有如下要求:一是要特别注意
真数大于零;二是要注意底数;三是按底数的取值应用单调性.
1-1.求下列函数的定义域:
1-2.求下列函数的值域:
函数图象问题
例
2:作函数
y=|log2(x+1)|+2
的图象.
思维突破:由
y=log2x
的图象,通过平移、对称变换得到
y=|log2(x+1)|+2
的图象.
图
2
图
2
一般地,要得到
y=f(x+a)+b
的图象,可
把
y=f(x)沿
x
轴向右(a<0)或向左(a>0)平移|a|个单位,再沿
y
轴
方向向上(b>0)或向下(b<0)平移|b|个单位.而要得到
y=|f(x)|的
图象,则可对
y=f(x)在
x
轴下方的图象作关于
x
轴的对称变换,
同时保留其在
x
轴上方的图象.
C
利用函数性质比较大小
例
3:比较下列三组数的大小关系:
思维突破:若同底,则利用相应函数单调性解决;不同底,
可考虑化同底或与
1,0
比大小,或借助图象观察得到结论.
利用对数函数的单调性进行对数值的大小
比较,常用的方法如下:①若底数为同一常数,则可由对数函
数的单调性直接判断;②若底数为同一字母,则按对数函数的
单调性对底数进行分类讨论;③若底数不同,真数相同,则可
用换底公式化为同底,再进行比较;④若底数、真数都不相同,
则常借助
1,0,-1
等中间量进行比较或利用对数函数图象的性
质进行判断.
3-1.已知
loga3>logb3,试比较
a
与
b
的大小.
例
4:设函数
y=f(x),且
lg(lgy)=lg3x+lg(3-x),求:
(1)f(x)的表达式及定义域;
(2)f(x)的值域.
错因剖析:没有考虑所给式子的限制,所求函数的定义域
必须使原式有意义,不能仅根据对数符号所得的解析式去确定
函数的定义域.
