沪教版(上海)高中数学高一下册 6.1 正弦函数和余弦函数的图像与性质(课件)(共17张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 6.1 正弦函数和余弦函数的图像与性质(课件)(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 23:10:02 | ||
图片预览





文档简介
(共17张PPT)
斗
奋
拼
搏
1、了解利用单位圆中的三角函数线作正余弦函数图象
2、会用”五点作图法”作正余弦函数的简图
3、掌握正余弦函数图象之间的关系
学
习
目
标
通过上述实验我们对正弦函数和余弦函数图象有了直观印象.但如何画出相对精确图象呢
思考:
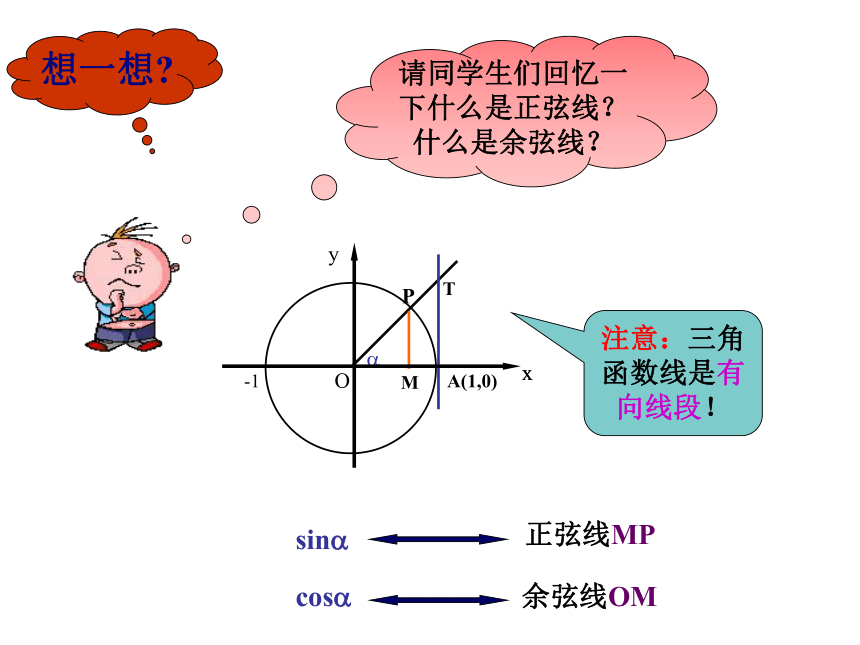
想一想
请同学生们回忆一下什么是正弦线?什么是余弦线?
-1
P
M
A(1,0)
T
注意:三角函数线是有向线段!
y
x
x
O
正弦线MP
sin
cos
余弦线OM
想一想
我们可以用单位圆中的三角函数线来刻画三角函数,是否可以用它来帮助我们作出三角函数的图象呢
思考:
想一想
O1
O
y
x
-1
1
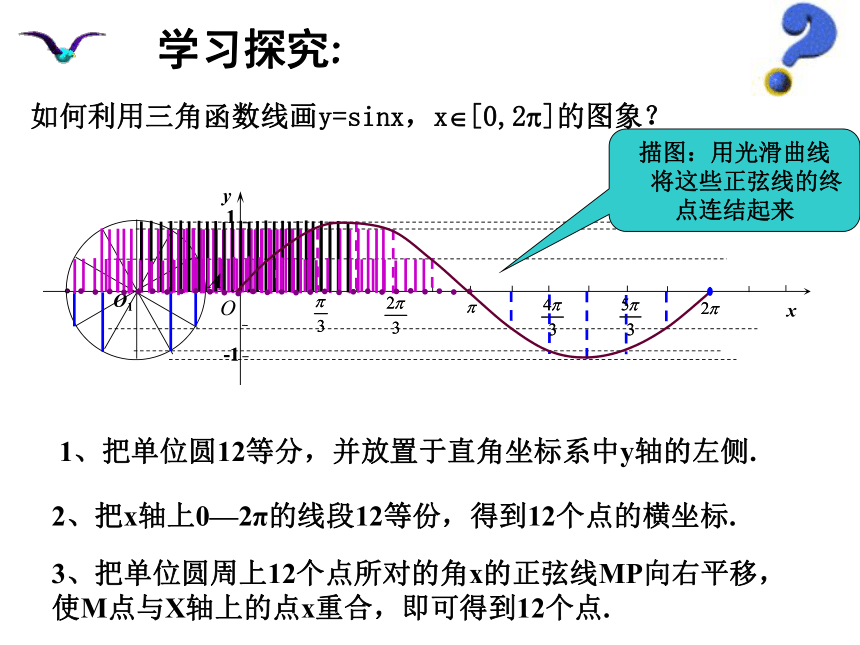
描图:用光滑曲线
将这些正弦线的终点连结起来
A
2、把x轴上0—2π的线段12等份,得到12个点的横坐标.
1、把单位圆12等分,并放置于直角坐标系中y轴的左侧.
3、把单位圆周上12个点所对的角x的正弦线MP向右平移,使M点与X轴上的点x重合,即可得到12个点.
如何利用三角函数线画y=sinx,x [0,2 ]的图象?
学习探究:
-1
1
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx
x [0,2 ]
y=sinx
x R
正弦曲线
y
x
o
1
-1
学习探究:
如何由
的图象得到
的图象
y=sinx
x [0,2 ]
y=sinx
x R
由部分到整体
y=sinx
x [0,2 ]
y=sinx
x R
sin(x+2k )=sinx,
k Z
利用图象平移
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx与
y=sin(x+
),
x R图象相同
余弦曲线
正弦曲线
形状完全一样只是位置不同
合作探究
你能根据诱导公式,以正弦函数的图象为基础,通过适当的图形变换得到余弦函数的图象吗?
由未知向已知转化
由诱导公式y=
,将正弦函数的图象向左平移
个单位即可得到余弦函数的图象.
在精确度要求不太高时,如何快捷地作出正弦函数的图象呢?
在作出正弦函数的图象时,应抓住哪些
关键点?
思考?
与x轴的交点
图象的最高点
图象的最低点
与x轴的交点
图象的最高点
图象的最低点
简图作法
(五点作图法)
(1)
列表(列出对图象形状起关键作用的五点坐标)
(2)
描点(定出五个关键点)
(3)
连线(用光滑的曲线顺次连结五个点)
五点作图法
描点作图
-
-
-
例1.画出下列函数的简图
(1)y=sinx+1,
x∈[0,2π]
(2)y=-cosx
,
x∈[0,2π]
列表
解:
(1)
-
-
(2)
1
0
-1
0
1
-1
0
1
0
-1
典型例题
五点法作图
(2)描点
(1)列表
(3)连线
思考:能否从图象变换的角度出发得到(1)(2)的图象?
1.用五点法画出y=sinx+2,x∈[0,
]的简图;
2.用五点法画出y=sinx-1,x∈[0,
]的简图;
2π
x
y
o
-1
1
2
2
.
.
.
.
.
1.用五点法画出y=sinx+2,x∈[0,
]的简图
y=sinx+2,
x∈[0,
]
x
y
o
-1
1
2
2
.
.
.
.
.
2.用五点法画出y=sinx-1,x∈[0,
]的简图
y=sinx-1,
x∈[0,
]
归纳小结
1.
正弦曲线、余弦曲线特点
2.注意与诱导公式、三角函数线等知识的联系
y
x
o
1
-1
y=sinx,x [0,
2 ]
y=cosx,x [0,
2 ]
3.数学思想
课
后
作
业
1.课本习题1.4第1题
2.课外查找单位圆中的三角函数线和三角函数的图象资料
X
斗
奋
拼
搏
1、了解利用单位圆中的三角函数线作正余弦函数图象
2、会用”五点作图法”作正余弦函数的简图
3、掌握正余弦函数图象之间的关系
学
习
目
标
通过上述实验我们对正弦函数和余弦函数图象有了直观印象.但如何画出相对精确图象呢
思考:
想一想
请同学生们回忆一下什么是正弦线?什么是余弦线?
-1
P
M
A(1,0)
T
注意:三角函数线是有向线段!
y
x
x
O
正弦线MP
sin
cos
余弦线OM
想一想
我们可以用单位圆中的三角函数线来刻画三角函数,是否可以用它来帮助我们作出三角函数的图象呢
思考:
想一想
O1
O
y
x
-1
1
描图:用光滑曲线
将这些正弦线的终点连结起来
A
2、把x轴上0—2π的线段12等份,得到12个点的横坐标.
1、把单位圆12等分,并放置于直角坐标系中y轴的左侧.
3、把单位圆周上12个点所对的角x的正弦线MP向右平移,使M点与X轴上的点x重合,即可得到12个点.
如何利用三角函数线画y=sinx,x [0,2 ]的图象?
学习探究:
-1
1
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx
x [0,2 ]
y=sinx
x R
正弦曲线
y
x
o
1
-1
学习探究:
如何由
的图象得到
的图象
y=sinx
x [0,2 ]
y=sinx
x R
由部分到整体
y=sinx
x [0,2 ]
y=sinx
x R
sin(x+2k )=sinx,
k Z
利用图象平移
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx与
y=sin(x+
),
x R图象相同
余弦曲线
正弦曲线
形状完全一样只是位置不同
合作探究
你能根据诱导公式,以正弦函数的图象为基础,通过适当的图形变换得到余弦函数的图象吗?
由未知向已知转化
由诱导公式y=
,将正弦函数的图象向左平移
个单位即可得到余弦函数的图象.
在精确度要求不太高时,如何快捷地作出正弦函数的图象呢?
在作出正弦函数的图象时,应抓住哪些
关键点?
思考?
与x轴的交点
图象的最高点
图象的最低点
与x轴的交点
图象的最高点
图象的最低点
简图作法
(五点作图法)
(1)
列表(列出对图象形状起关键作用的五点坐标)
(2)
描点(定出五个关键点)
(3)
连线(用光滑的曲线顺次连结五个点)
五点作图法
描点作图
-
-
-
例1.画出下列函数的简图
(1)y=sinx+1,
x∈[0,2π]
(2)y=-cosx
,
x∈[0,2π]
列表
解:
(1)
-
-
(2)
1
0
-1
0
1
-1
0
1
0
-1
典型例题
五点法作图
(2)描点
(1)列表
(3)连线
思考:能否从图象变换的角度出发得到(1)(2)的图象?
1.用五点法画出y=sinx+2,x∈[0,
]的简图;
2.用五点法画出y=sinx-1,x∈[0,
]的简图;
2π
x
y
o
-1
1
2
2
.
.
.
.
.
1.用五点法画出y=sinx+2,x∈[0,
]的简图
y=sinx+2,
x∈[0,
]
x
y
o
-1
1
2
2
.
.
.
.
.
2.用五点法画出y=sinx-1,x∈[0,
]的简图
y=sinx-1,
x∈[0,
]
归纳小结
1.
正弦曲线、余弦曲线特点
2.注意与诱导公式、三角函数线等知识的联系
y
x
o
1
-1
y=sinx,x [0,
2 ]
y=cosx,x [0,
2 ]
3.数学思想
课
后
作
业
1.课本习题1.4第1题
2.课外查找单位圆中的三角函数线和三角函数的图象资料
X
