宁夏银川第一重点高中2022届高三上学期第二次月考数学(理)试题(Word版含答案)
文档属性
| 名称 | 宁夏银川第一重点高中2022届高三上学期第二次月考数学(理)试题(Word版含答案) | 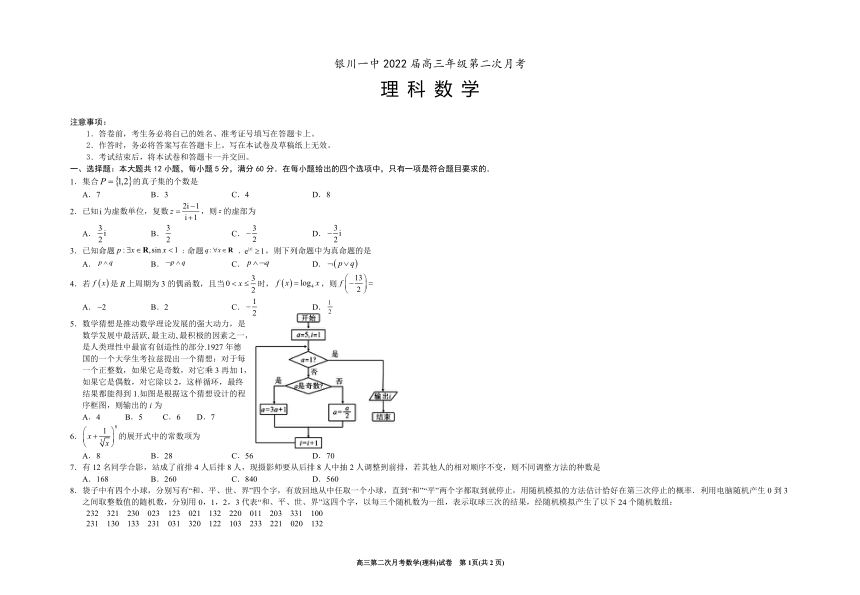 | |
| 格式 | doc | ||
| 文件大小 | 932.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-02 21:25:02 | ||
图片预览




文档简介
银川一中2022届高三年级第二次月考
理
科
数
学
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合的真子集的个数是
A.7
B.3
C.4
D.8
2.已知为虚数单位,复数,则的虚部为
A.
B.
C.
D.
3.已知命题﹔命题﹐,则下列命题中为真命题的是
A.
B.
C.
D.
4.若是上周期为3的偶函数,且当时,,则
A.
B.2
C.
D.
5.数学猜想是推动数学理论发展的强大动力,是
数学发展中最活跃 最主动 最积极的因素之一,
是人类理性中最富有创造性的部分.1927年德
国的一个大学生考拉兹提出一个猜想:对于每
一个正整数,如果它是奇数,对它乘3再加1,
如果它是偶数,对它除以2,这样循环,最终
结果都能得到1.如图是根据这个猜想设计的程
序框图,则输出的i为
A.4
B.5
C.6
D.7
6.的展开式中的常数项为
A.8
B.28
C.56
D.70
7.有12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是
A.168
B.260
C.840
D.560
8.袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到“和”“平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:
232
321
230
023
123
021
132
220
011
203
331
100
231
130
133
231
031
320
122
103
233
221
020
132
由此可以估计,恰好第三次就停止的概率为
A.
B.
C.
D.
9.
A.
B.
C.
D.
10.把不超过实数x的最大整数记为[x],则函数f(x)=[x]称作取整函数,又叫高斯函数,在[2,5]上任取x,则[x]=[]的概率为
A.
B.
C.
D.
11.已知定义域为的函数满足,且,则下列结论一定正确的是(
)
A.
B.函数的图象关于点对称
C.函数是奇函数
D.
12.已知定义在上的函数满足,且当时,,若方程有三个不同的实数根,则实数的取值范围是
A.
B.
C.
D.
二、填空题:(本大题共4小题,每小题5分,共20分)
13.已知函数,则在处的切线方程是________.
14.在一个不透明的袋中装有5个白球,3个红球(除颜色外其他均相同),从中任意取出2个小球,记事件为“取出的球中有红色小球”,事件为“取出的2个小球均是红球”,则__________.
15.一道四个选项的选择题,赵、钱、孙、李各选了一个选项,且选的恰好各不相同.
赵说:“我选的是A.”
钱说:“我选的是B,C,D之一.”
孙说:“我选的是C.”
李说:“我选的是D.”
已知四人中只有一人说了假话,则说假话的人可能是__________.
16.已知函数.下面四个结论
①是奇函数
②在上为增函数
③若,则
④对任意实数x恒成立
其中正确的是__________.
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分
17.
(12分)
设,其中为实数.
(1)设集合,集合,若,求实数的取值范围;
(2)若集合中的元素有且仅有2个,求实数的取值范围.
18.(12分)
设函数
(1)当时,求曲线的极值;
(2)若函数在区间内单调递减,求的取值范围.
19.(12分)
核酸检测是诊断新冠肺炎的重要依据,首先取病人的唾液或咽拭子的样本,再提取唾液或咽拭子样本里的遗传物质,如果有病毒,样本检测会呈现阳性,否则为阴性.某检测点根据统计发现,该处疑似病例核酸检测呈阳性的概率为.现有4例疑似病例,分别对其取样检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有病毒,则混合样本化验结果就会呈阳性.若混合样本呈阳性,则再将该组中每一个备份的样本逐一进行化验;若混合样本呈阴性,则判定该组各个样本均为阴性,无需再检验.现有以下三种方案:
方案一:逐个化验;
方案二:四个样本混合在一起化验;
方案三:平均分成两组,每组两个样本混合在一起,再分组化验.
在新冠肺炎爆发初期,由于检查能力不足,化验次数的期望值越小,则方案越“优”.
(1)求4个疑似病例中至少有1例呈阳性的概率;
(2)现将该4例疑似病例样本进行化验,请问:方案一、二、三中哪个最“优”?做出判断并说明理由.
(12分)
2021年3月1日,国务院新闻办公室举行新闻发布会,工业和信息化部长肖亚庆先生提出了芯片发展的五项措施,进一步激励国内科技巨头加大了科技研发投入的力度.中华技术有限公司拟对“麒麟”手机芯片进行科技升级,根据市场调研与模拟,得到科技升级投入(亿元)与科技升级直接纯收益(亿元)的数据统计如下:
序号
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
6
8
10
13
21
22
23
24
25
13
22
31
42
50
56
58
68.5
68
67.5
66
66
当时,建立了与的两个回归模型:模型①:;模型②:;当时,确定与满足的线性回归方程为.
(1)根据下列表格中的数据,比较当时模型①、②的相关指数的大小,并选择拟合精度更高、更可靠的模型.
回归模型
模型①
模型②
回归方程
182.4
79.2
(附:刻画回归效果的相关指数,)
(2)为鼓励科技创新,当科技升级的投入不少于20亿元时,国家给予公司补贴5亿元,以回归方程为预测依据,应用(1)的结论,比较科技升级投入17亿元与20亿元时公司实际收益的大小.
(附:线性回归方程的系数关系:)
(3)科技升级后,“麒麟”芯片的效率大幅提高,经实际试验得大致服从正态分布.公司对科技升级团队的奖励方案如下:若芯片的效率不超过,不予奖励:若芯片的效率超过,但不超过,每部芯片奖励2元;若芯片的效率超过,每部芯片奖励4元.记为每部芯片获得的奖励,求(精确到0.01).
(附:若随机变量,则,)
21.
(12分)
已知函数f(x)=ex-1,g(x)=lnx-1,其中e为自然对数的底数.
(1)当x>0时,求证:f(x)≥g(x)+2;
(2)是否存在直线与函数y=f(x)及y=g(x)的图象均相切?若存在,这样的直线最多有几条?并给出证明.若不存在,请说明理由.
(二)选考题:共10分。请考生在第22、23两题中任选一题做答,如果多做.则按所做的第一题记分。
22.[选修4-4:坐标系与参数方程]
在平面直角坐标系中,以为极点、轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为,直线过定点且与曲线交于,两点.
(1)求曲线的直角坐标方程;
(2)若直线的斜率为2,求的值.
23.[选修4—5:不等式选讲]
已知函数.
(1)若,求不等式的解集;
(2)若,使得,求的取值范围.
银川一中2022届高三第二次月考数学(理科)(参考答案)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
A
C
C
B
C
A
B
B
B
D
二、填空题
13.
14.
15.
孙
李
16
.
2
3
4
三、解答题
17.解:(1)化简,
又,所以
(2)由,
得等价于,且,
设,在上严格增,
在上严格减,g(1)=1,g(3)=3,
g(x)在(0,3)内的图象如图所示.
由题意等价于直线与函数
在上恰有两个交点,
此时.
18.解:(1)∵,,,
,所以函数在x=-
处取得极小值
(2)
∵函数在区间内单调递减,
∴在区间上恒成立;
即,∵
∴
即在区间上恒成立
∴,解得,
∴的取值范围是
19.【解】
(1)用表示4个疑似病例中化验呈阳性的人数,则,
由题意可知,4个疑似病例中至少有1例呈阳性的概率为
;
(2)方案一:逐个检验,检验次数为4.
方案二:混合在一起检测,记检测次数为,则随机变量的可能取值为1,5,所以
,
,
所以随机变量的分布列为:
1
5
所以方案二检测次数的数学期望为;
方案三:每组两个样本检测时,呈阴性的概率为,
设方案三的检测次数为随机变量,则的可能取值为2,4,6,所以
,
,
,
所以随机变量的分布列为:
2
4
6
所以方案三检测次数的期望为,
因为,
所以选择方案二最优.
20
【解】
(1)由表格中的数据,,所以,
所以.
可见模型①的相关指数小于模型②的相关指数.
所以回归模型②的拟合效果更好.
(2)由(1)回归模型②的拟合效果更好,其回归方程为,
所以当亿元时,科技升级直接收益的预测值为
(亿元).
当时,由已知可得.
.
所以.
所以当时,与满足的线性回归方程为.
当时,科技升级直接收益的预测值为亿元.
当亿元时,实际收益的预测值为亿元亿元,
所以技术升级投入亿元时,公司的实际收益更大.
(3)因为,,
所以
;
.
所以(元).
21
解(1)设,,.
因为在为增函数,且,
所以,,为减函数,
,,为增函数.
所以,,即证.
(2)设直线与切于,与切于,.
,,,
所以切线为.
因为,即,即.
又因为,
将,代入,
得:,整理得.
设,,
因为在为增函数,且时,,
所以,,为减函数,
,,为增函数.
,
又因为,
,
所以在上有两个零点,
即方程有两个根,
所以有两条直线与函数及的图象均相切.
22.(1);(2).
【详解】
(1)由得.
于是,∴,
所以曲线的直角坐标方程为.
(2)设直线的倾斜角为,则,于是,,
所以直线的参数方程为(为参数).
将,代入得,
所以,,
所以.
23.(1)或};(2)答案见解析.
【详解】
解:(1)当时,.
当时,,所以;
当时,,不成立;
当时,,所以,
所以,综上可知,所求解集为或}.
(2)要求,使得时,的取值范围,
可先求,使得时,的取值范围,
,,
当时,恒成立;
当时,,
综上,,使得时,的取值范围为,
故,使得时,的取值范围为.
高三第二次月考数学(理科)试卷
第1页(共2页)
理
科
数
学
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合的真子集的个数是
A.7
B.3
C.4
D.8
2.已知为虚数单位,复数,则的虚部为
A.
B.
C.
D.
3.已知命题﹔命题﹐,则下列命题中为真命题的是
A.
B.
C.
D.
4.若是上周期为3的偶函数,且当时,,则
A.
B.2
C.
D.
5.数学猜想是推动数学理论发展的强大动力,是
数学发展中最活跃 最主动 最积极的因素之一,
是人类理性中最富有创造性的部分.1927年德
国的一个大学生考拉兹提出一个猜想:对于每
一个正整数,如果它是奇数,对它乘3再加1,
如果它是偶数,对它除以2,这样循环,最终
结果都能得到1.如图是根据这个猜想设计的程
序框图,则输出的i为
A.4
B.5
C.6
D.7
6.的展开式中的常数项为
A.8
B.28
C.56
D.70
7.有12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是
A.168
B.260
C.840
D.560
8.袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到“和”“平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:
232
321
230
023
123
021
132
220
011
203
331
100
231
130
133
231
031
320
122
103
233
221
020
132
由此可以估计,恰好第三次就停止的概率为
A.
B.
C.
D.
9.
A.
B.
C.
D.
10.把不超过实数x的最大整数记为[x],则函数f(x)=[x]称作取整函数,又叫高斯函数,在[2,5]上任取x,则[x]=[]的概率为
A.
B.
C.
D.
11.已知定义域为的函数满足,且,则下列结论一定正确的是(
)
A.
B.函数的图象关于点对称
C.函数是奇函数
D.
12.已知定义在上的函数满足,且当时,,若方程有三个不同的实数根,则实数的取值范围是
A.
B.
C.
D.
二、填空题:(本大题共4小题,每小题5分,共20分)
13.已知函数,则在处的切线方程是________.
14.在一个不透明的袋中装有5个白球,3个红球(除颜色外其他均相同),从中任意取出2个小球,记事件为“取出的球中有红色小球”,事件为“取出的2个小球均是红球”,则__________.
15.一道四个选项的选择题,赵、钱、孙、李各选了一个选项,且选的恰好各不相同.
赵说:“我选的是A.”
钱说:“我选的是B,C,D之一.”
孙说:“我选的是C.”
李说:“我选的是D.”
已知四人中只有一人说了假话,则说假话的人可能是__________.
16.已知函数.下面四个结论
①是奇函数
②在上为增函数
③若,则
④对任意实数x恒成立
其中正确的是__________.
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分
17.
(12分)
设,其中为实数.
(1)设集合,集合,若,求实数的取值范围;
(2)若集合中的元素有且仅有2个,求实数的取值范围.
18.(12分)
设函数
(1)当时,求曲线的极值;
(2)若函数在区间内单调递减,求的取值范围.
19.(12分)
核酸检测是诊断新冠肺炎的重要依据,首先取病人的唾液或咽拭子的样本,再提取唾液或咽拭子样本里的遗传物质,如果有病毒,样本检测会呈现阳性,否则为阴性.某检测点根据统计发现,该处疑似病例核酸检测呈阳性的概率为.现有4例疑似病例,分别对其取样检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有病毒,则混合样本化验结果就会呈阳性.若混合样本呈阳性,则再将该组中每一个备份的样本逐一进行化验;若混合样本呈阴性,则判定该组各个样本均为阴性,无需再检验.现有以下三种方案:
方案一:逐个化验;
方案二:四个样本混合在一起化验;
方案三:平均分成两组,每组两个样本混合在一起,再分组化验.
在新冠肺炎爆发初期,由于检查能力不足,化验次数的期望值越小,则方案越“优”.
(1)求4个疑似病例中至少有1例呈阳性的概率;
(2)现将该4例疑似病例样本进行化验,请问:方案一、二、三中哪个最“优”?做出判断并说明理由.
(12分)
2021年3月1日,国务院新闻办公室举行新闻发布会,工业和信息化部长肖亚庆先生提出了芯片发展的五项措施,进一步激励国内科技巨头加大了科技研发投入的力度.中华技术有限公司拟对“麒麟”手机芯片进行科技升级,根据市场调研与模拟,得到科技升级投入(亿元)与科技升级直接纯收益(亿元)的数据统计如下:
序号
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
6
8
10
13
21
22
23
24
25
13
22
31
42
50
56
58
68.5
68
67.5
66
66
当时,建立了与的两个回归模型:模型①:;模型②:;当时,确定与满足的线性回归方程为.
(1)根据下列表格中的数据,比较当时模型①、②的相关指数的大小,并选择拟合精度更高、更可靠的模型.
回归模型
模型①
模型②
回归方程
182.4
79.2
(附:刻画回归效果的相关指数,)
(2)为鼓励科技创新,当科技升级的投入不少于20亿元时,国家给予公司补贴5亿元,以回归方程为预测依据,应用(1)的结论,比较科技升级投入17亿元与20亿元时公司实际收益的大小.
(附:线性回归方程的系数关系:)
(3)科技升级后,“麒麟”芯片的效率大幅提高,经实际试验得大致服从正态分布.公司对科技升级团队的奖励方案如下:若芯片的效率不超过,不予奖励:若芯片的效率超过,但不超过,每部芯片奖励2元;若芯片的效率超过,每部芯片奖励4元.记为每部芯片获得的奖励,求(精确到0.01).
(附:若随机变量,则,)
21.
(12分)
已知函数f(x)=ex-1,g(x)=lnx-1,其中e为自然对数的底数.
(1)当x>0时,求证:f(x)≥g(x)+2;
(2)是否存在直线与函数y=f(x)及y=g(x)的图象均相切?若存在,这样的直线最多有几条?并给出证明.若不存在,请说明理由.
(二)选考题:共10分。请考生在第22、23两题中任选一题做答,如果多做.则按所做的第一题记分。
22.[选修4-4:坐标系与参数方程]
在平面直角坐标系中,以为极点、轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为,直线过定点且与曲线交于,两点.
(1)求曲线的直角坐标方程;
(2)若直线的斜率为2,求的值.
23.[选修4—5:不等式选讲]
已知函数.
(1)若,求不等式的解集;
(2)若,使得,求的取值范围.
银川一中2022届高三第二次月考数学(理科)(参考答案)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
A
C
C
B
C
A
B
B
B
D
二、填空题
13.
14.
15.
孙
李
16
.
2
3
4
三、解答题
17.解:(1)化简,
又,所以
(2)由,
得等价于,且,
设,在上严格增,
在上严格减,g(1)=1,g(3)=3,
g(x)在(0,3)内的图象如图所示.
由题意等价于直线与函数
在上恰有两个交点,
此时.
18.解:(1)∵,,,
,所以函数在x=-
处取得极小值
(2)
∵函数在区间内单调递减,
∴在区间上恒成立;
即,∵
∴
即在区间上恒成立
∴,解得,
∴的取值范围是
19.【解】
(1)用表示4个疑似病例中化验呈阳性的人数,则,
由题意可知,4个疑似病例中至少有1例呈阳性的概率为
;
(2)方案一:逐个检验,检验次数为4.
方案二:混合在一起检测,记检测次数为,则随机变量的可能取值为1,5,所以
,
,
所以随机变量的分布列为:
1
5
所以方案二检测次数的数学期望为;
方案三:每组两个样本检测时,呈阴性的概率为,
设方案三的检测次数为随机变量,则的可能取值为2,4,6,所以
,
,
,
所以随机变量的分布列为:
2
4
6
所以方案三检测次数的期望为,
因为,
所以选择方案二最优.
20
【解】
(1)由表格中的数据,,所以,
所以.
可见模型①的相关指数小于模型②的相关指数.
所以回归模型②的拟合效果更好.
(2)由(1)回归模型②的拟合效果更好,其回归方程为,
所以当亿元时,科技升级直接收益的预测值为
(亿元).
当时,由已知可得.
.
所以.
所以当时,与满足的线性回归方程为.
当时,科技升级直接收益的预测值为亿元.
当亿元时,实际收益的预测值为亿元亿元,
所以技术升级投入亿元时,公司的实际收益更大.
(3)因为,,
所以
;
.
所以(元).
21
解(1)设,,.
因为在为增函数,且,
所以,,为减函数,
,,为增函数.
所以,,即证.
(2)设直线与切于,与切于,.
,,,
所以切线为.
因为,即,即.
又因为,
将,代入,
得:,整理得.
设,,
因为在为增函数,且时,,
所以,,为减函数,
,,为增函数.
,
又因为,
,
所以在上有两个零点,
即方程有两个根,
所以有两条直线与函数及的图象均相切.
22.(1);(2).
【详解】
(1)由得.
于是,∴,
所以曲线的直角坐标方程为.
(2)设直线的倾斜角为,则,于是,,
所以直线的参数方程为(为参数).
将,代入得,
所以,,
所以.
23.(1)或};(2)答案见解析.
【详解】
解:(1)当时,.
当时,,所以;
当时,,不成立;
当时,,所以,
所以,综上可知,所求解集为或}.
(2)要求,使得时,的取值范围,
可先求,使得时,的取值范围,
,,
当时,恒成立;
当时,,
综上,,使得时,的取值范围为,
故,使得时,的取值范围为.
高三第二次月考数学(理科)试卷
第1页(共2页)
同课章节目录
