安徽省滁州市定远县育才学校2021-2022学年高二上学期理科数学周测1(9月27日)(Word版含答案解析)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2021-2022学年高二上学期理科数学周测1(9月27日)(Word版含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-02 21:34:02 | ||
图片预览



文档简介
定远育才学校高二年级数学学科
周测试卷2(理科)(空间向量的应用)
总分:100分
时间:100分钟
2021年9月27日
一、选择题(共10小题,每小题5分,共50分)
1.已知直线l1的方向向量a=(-1,2,m),直线l2的方向向量b=(2,n,-12),且l1∥l2,则m+3n的值是( )
A.
-6
B.
6
C.
14
D.
-14
2.在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=,则异面直线AD1与DB1所成角的余弦值为( )A.
B.
C.
D.
3.已知点A(1-t,1-t,t),B(2,t,t),则A,B两点的距离的最小值为( )A.
B.
C.
D.
4.已知两平面的法向量分别为m=(1,-1,0),n=(0,1,-1),则两平面的夹角为( )A.
60°
B.
120°
C.
60°或120°
D.
90°
5.如图,将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足=-+,则||2的值为( )
A.
B.
3
C.
D.
6.正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,BC,CD,BB1的中点,则下列结论正确的是( )
A.B1G⊥BC
B.平面AEF∩平面AA1D1D=AD1
C.A1H∥平面AEF
D.平面EAF与平面AFC的夹角为
7.在四面体ABCD中,AB,BC,BD两两垂直,且AB=BC=1,点E是AC的中点,异面直线AD与BE所成角为θ,且cosθ=,则该四面体的体积为( )A.
B.
C.
D.
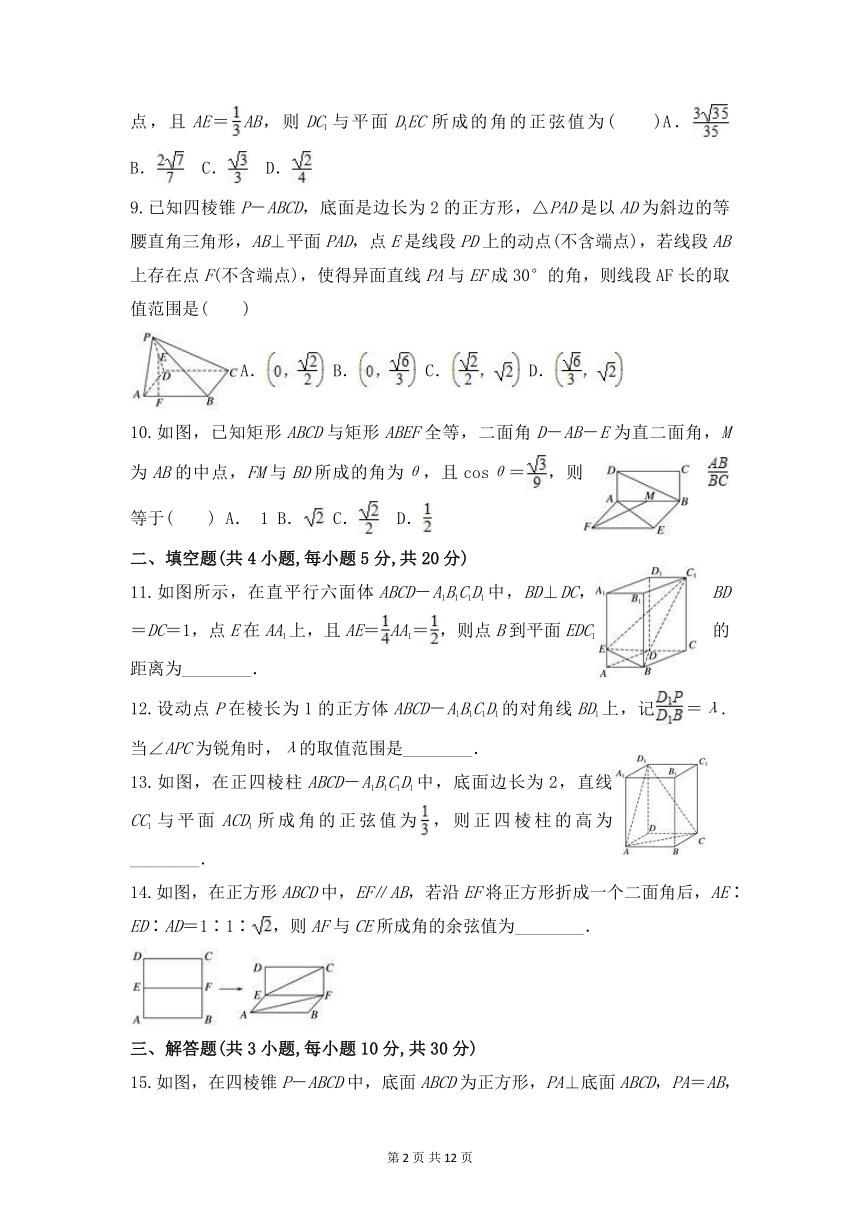
8.如图,已知长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=3,E为线段AB上一点,且AE=AB,则DC1与平面D1EC所成的角的正弦值为( )A.
B.
C.
D.
9.已知四棱锥P-ABCD,底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,点E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA与EF成30°的角,则线段AF长的取值范围是( )
A.
B.
C.
D.
10.如图,已知矩形ABCD与矩形ABEF全等,二面角D-AB-E为直二面角,M为AB的中点,FM与BD所成的角为θ,且cosθ=,则等于( )
A.
1
B.
C.
D.
二、填空题(共4小题,每小题5分,共20分)
11.如图所示,在直平行六面体ABCD-A1B1C1D1中,BD⊥DC,BD=DC=1,点E在AA1上,且AE=AA1=,则点B到平面EDC1的距离为________.
12.设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记=λ.当∠APC为锐角时,λ的取值范围是________.
13.如图,在正四棱柱ABCD-A1B1C1D1中,底面边长为2,直线CC1与平面ACD1所成角的正弦值为,则正四棱柱的高为________.
14.如图,在正方形ABCD中,EF∥AB,若沿EF将正方形折成一个二面角后,AE∶ED∶AD=1∶1∶,则AF与CE所成角的余弦值为________.
三、解答题(共3小题,每小题10分,共30分)
15.如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AB,E为线段PB的中点.
(1)求证:点F在线段BC上移动时,△AEF为直角三角形;
(2)若F为线段BC的中点,求平面AEF与平面EFD夹角的余弦值.
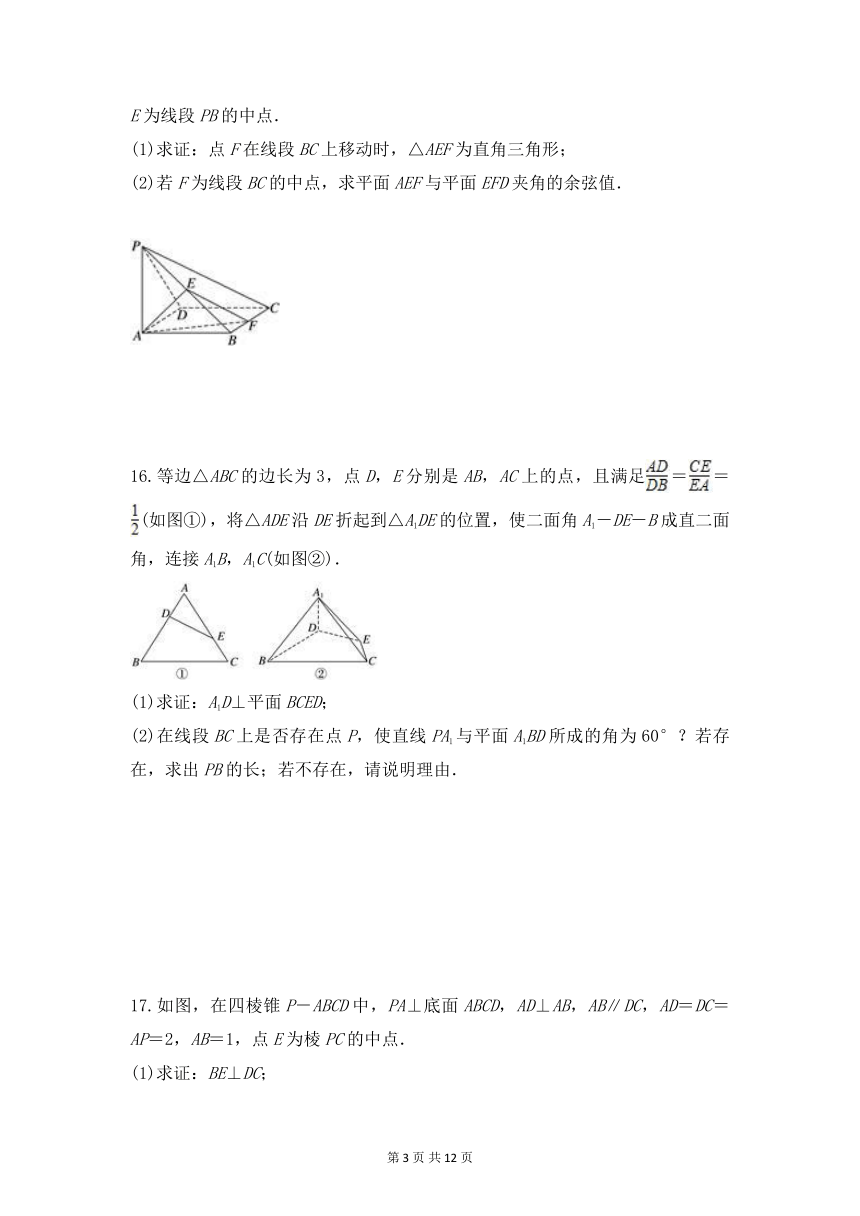
16.等边△ABC的边长为3,点D,E分别是AB,AC上的点,且满足==(如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B成直二面角,连接A1B,A1C(如图②).
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长;若不存在,请说明理由.
17.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)求证:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求平面FAB与平面ABP夹角的余弦值.
答案解析
1.【答案】A
【解析】∵l1∥l2,∴a∥b,
则==,
解得n=-4,m=6,
∴m+3n=6-12=-6.
2.【答案】C
【解析】以D为坐标原点,DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系(图略),
则D(0,0,0),A(1,0,0),B1(1,1,),D1(0,0,),
所以=(-1,0,),=(1,1,),
因为|cos〈,〉|===.
所以异面直线AD1与DB1所成角的余弦值为.
3.【答案】C
【解析】因为点A(1-t,1-t,t),B(2,t,t),
所以|AB|2=(1+t)2+(2t-1)2+(t-t)2=5t2-2t+2,
由二次函数易知,当t=时,取得最小值为,
所以|AB|的最小值为.
4.【答案】A
【解析】|cos〈m,n〉|===,
即〈m,n〉=60°.
∴两平面所成角为60°.
5.【答案】D
【解析】由题可知||=1,||=1,||=.
〈,〉=45°,〈,〉=45°,〈,〉=60°,
所以||2=2=2+2+2-·+·-·=++2-×1×1×+1××-1××=.
6.【答案】BC
【解析】由题意可知,B1G在底面上的射影为BG,而BC不垂直BG,则B1G不垂直于BC,则选项A不正确;
连接AD1和BC1,由E,F,G,H分别为CC1,BC,CD,BB1的中点,可知EF∥BC1∥AD1,则平面AEF∩平面AA1D1D=AD1,所以选项B正确;
由题知,可设正方体的棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,则各点坐标如下:A(2,0,0),E(0,2,1),A1(2,0,2),H(2,2,1),F(1,2,0),=(0,2,-1),=(-1,2,0),=(1,0,-1),=(0,0,2),设平面AEF的法向量为n=(x,y,z),则即令y=1,得x=2,z=2,得平面AEF的法向量为n=(2,1,2),所以·n=0,所以A1H∥平面AEF,则C选项正确;
由图可知,AA1⊥平面AFC,所以是平面AFC的法向量,则cos〈,n〉==.平面EAF与平面AFC的夹角的大小不是,所以D不正确.
7.【答案】A
【解析】分别以BC,BA,BD所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,设BD=a,
则A(0,1,0),B(0,0,0),E,D(0,0,a)
,
=(0,-1,a),=,
cosθ=
=
=,
解得a=2,
该四面体的体积为××1×1×2=.
8.【答案】A
【解析】如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则C1(0,3,1),D1(0,0,1),E(1,1,0),C(0,3,0),
所以=(0,3,1),=(1,1,-1),=(0,3,-1).
设平面D1EC的法向量为n=(x,y,z),
则
即即
取y=1,得n=(2,1,3).
因为cos〈,n〉===,
所以DC1与平面D1EC所成的角的正弦值为.
9.【答案】B
【解析】由△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,取AD中点G,建立如图所示的空间直角坐标系,
依题意G(0,0,0),A(1,0,0),D(-1,0,0),B(1,2,0),P(0,0,1),设F(1,y,0),
设=x=x(1,0,1)=(x,0,x),0又=(1,0,-1),异面直线PA与EF成30°的角,
故|·|=||·||cos
30°,
即2=××,
即y2=-2(x-1)2+,0故y2∈,
又010.【答案】C
【解析】不妨设BC=1,AB=λ,则=λ,记=a,=b,=c,则=b-a,=c-b,根据题意,|a|=|c|=1,|b|=λ,a·b=b·c=c·a=0,所以·=-b2=-λ2,而||=,||=,所以|cos〈,〉|===,得λ=.
11.【答案】
【解析】建立如图所示的空间直角坐标系,
则D(0,0,0),A(1,-1,0),B(1,0,0),C(0,1,0),C1(0,1,2),
E,
∴=(0,1,2),=.
设平面EDC1的法向量为n=(x,y,z),
则
令z=1,则x=-,y=-2,
∴n=.
∴点B到平面EDC1的距离d===.
12.【答案】
【解析】建立如图所示的空间直角坐标系,
则A(1,0,0),C(0,1,0),
B(1,1,0),D1(0,0,1),
由=λ得P(λ,λ,1-λ),
则=(1-λ,-λ,λ-1),=(-λ,1-λ,λ-1),
因为∠APC为锐角,
所以·=(1-λ,-λ,λ-1)·(-λ,1-λ,λ-1)=(λ-1)(3λ-1)>0,
解得λ<或λ>1,
又因为动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,
所以λ的取值范围为0≤λ<.
13.【答案】4
【解析】以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设DD1=a,
则A(2,0,0),C(0,2,0),
D1(0,0,a),
故=(-2,2,0),=(-2,0,a),=(0,0,a),
设平面ACD1的一个法向量为n=(x,y,z),
则
可取n=,
故cos〈n,〉===,
又直线CC1与平面ACD1所成角的正弦值为,
∴=,
解得a=4.
14.【答案】
【解析】因为AE∶ED∶AD=1∶1∶,
所以AE⊥ED,即AE,DE,EF两两垂直,
所以建立如图所示的空间直角坐标系,
设AB=EF=CD=2,
则E(0,0,0),A(1,0,0),F(0,2,0),C(0,2,1),
所以=(-1,2,0),=(0,2,1),
所以cos〈,〉===,
所以AF与CE所成角的余弦值为.
15.【答案】(1)证明 ∵PA=AB,E为线段PB的中点,
∴AE⊥PB.
∵PA⊥底面ABCD,BC 平面ABCD,
∴PA⊥BC.
∵底面ABCD为正方形,
∴BC⊥AB.
又PA∩AB=A,PA,AB 平面PAB,
∴BC⊥平面PAB.
∵AE 平面PAB,
∴BC⊥AE.
∵PB∩BC=B,PB,BC 平面PBC,
∴AE⊥平面PBC.
∵EF 平面PBC,
∴AE⊥EF,
∴点F在线段BC上移动时,△AEF为直角三角形.
(2)解 如图,以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,连接DF,令PA=2,则A(0,0,0),B(2,0,0),E(1,0,1),F(2,1,0),D(0,2,0),
设平面AEF的法向量为m=(x,y,z),
则
可得取m=(1,-2,-1),
设平面DEF的法向量为n=(a,b,c),
则
可得取n=(1,2,3),
∴|cos〈m,n〉|==,
∴平面AEF与平面DEF夹角的余弦值为.
16.【答案】(1)证明 由已知可得AE=2,AD=1,∠A=60°.
从而DE==.
故AD2+DE2=AE2,
∴A1D⊥DE,BD⊥DE.
∴∠A1DB为二面角A1-DE-B的平面角.
又二面角A1-DE-B为直二面角,
∴∠A1DB=90°,
即A1D⊥DB.
∵DE∩DB=D,且DE,DB 平面BCED,
∴A1D⊥平面BCED.
(2)解 存在.
由(1)知ED⊥DB,A1D⊥平面BCED,以D为坐标原点,以射线DB,DE,DA1分别为x轴,y轴,z轴的正半轴建立空间直角坐标系,如图,
过P作PH∥DE交BD于点H,
设PB=2a(0≤2a≤3),
则BH=a,PH=a,DH=2-a,
易知A1(0,0,1),P(2-a,a,0),E(0,,0),
∴=(a-2,-a,1),
∵DE⊥平面A1BD,
∴平面A1BD的一个法向量为=(0,,0).
∵直线PA1与平面A1BD所成的角为60°,
∴sin
60°===,
解得a=.
∴PB=2a=,满足0≤2a≤3,符合题意.
∴在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°,此时PB=.
17.【答案】(1)证明 依题意,以点A为坐标原点建立空间直角坐标系(如图),可得A(0,0,0),B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得E(1,1,1),所以=(0,1,1),=(2,0,0),故·=0,所以BE⊥DC.
(2)解 =(1,2,0),=(-2,-2,2),=(2,2,0),=(1,0,0).
由点F在棱PC上,设=λ(0≤λ≤1),
故=+=+λ=(1-2λ,2-2λ,2λ).
由BF⊥AC,得·=0,
因此2(1-2λ)+2(2-2λ)=0,解得λ=,
即=.
设n1=(x,y,z)为平面FAB的法向量,
则
即
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
易知向量n2=(0,1,0)为平面ABP的一个法向量,
则cos〈n1,n2〉===-.
所以平面FAB与平面ABP夹角的余弦值为.
(
第
12
页
共
13
页
)
周测试卷2(理科)(空间向量的应用)
总分:100分
时间:100分钟
2021年9月27日
一、选择题(共10小题,每小题5分,共50分)
1.已知直线l1的方向向量a=(-1,2,m),直线l2的方向向量b=(2,n,-12),且l1∥l2,则m+3n的值是( )
A.
-6
B.
6
C.
14
D.
-14
2.在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=,则异面直线AD1与DB1所成角的余弦值为( )A.
B.
C.
D.
3.已知点A(1-t,1-t,t),B(2,t,t),则A,B两点的距离的最小值为( )A.
B.
C.
D.
4.已知两平面的法向量分别为m=(1,-1,0),n=(0,1,-1),则两平面的夹角为( )A.
60°
B.
120°
C.
60°或120°
D.
90°
5.如图,将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足=-+,则||2的值为( )
A.
B.
3
C.
D.
6.正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,BC,CD,BB1的中点,则下列结论正确的是( )
A.B1G⊥BC
B.平面AEF∩平面AA1D1D=AD1
C.A1H∥平面AEF
D.平面EAF与平面AFC的夹角为
7.在四面体ABCD中,AB,BC,BD两两垂直,且AB=BC=1,点E是AC的中点,异面直线AD与BE所成角为θ,且cosθ=,则该四面体的体积为( )A.
B.
C.
D.
8.如图,已知长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=3,E为线段AB上一点,且AE=AB,则DC1与平面D1EC所成的角的正弦值为( )A.
B.
C.
D.
9.已知四棱锥P-ABCD,底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,点E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA与EF成30°的角,则线段AF长的取值范围是( )
A.
B.
C.
D.
10.如图,已知矩形ABCD与矩形ABEF全等,二面角D-AB-E为直二面角,M为AB的中点,FM与BD所成的角为θ,且cosθ=,则等于( )
A.
1
B.
C.
D.
二、填空题(共4小题,每小题5分,共20分)
11.如图所示,在直平行六面体ABCD-A1B1C1D1中,BD⊥DC,BD=DC=1,点E在AA1上,且AE=AA1=,则点B到平面EDC1的距离为________.
12.设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记=λ.当∠APC为锐角时,λ的取值范围是________.
13.如图,在正四棱柱ABCD-A1B1C1D1中,底面边长为2,直线CC1与平面ACD1所成角的正弦值为,则正四棱柱的高为________.
14.如图,在正方形ABCD中,EF∥AB,若沿EF将正方形折成一个二面角后,AE∶ED∶AD=1∶1∶,则AF与CE所成角的余弦值为________.
三、解答题(共3小题,每小题10分,共30分)
15.如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AB,E为线段PB的中点.
(1)求证:点F在线段BC上移动时,△AEF为直角三角形;
(2)若F为线段BC的中点,求平面AEF与平面EFD夹角的余弦值.
16.等边△ABC的边长为3,点D,E分别是AB,AC上的点,且满足==(如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B成直二面角,连接A1B,A1C(如图②).
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长;若不存在,请说明理由.
17.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)求证:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求平面FAB与平面ABP夹角的余弦值.
答案解析
1.【答案】A
【解析】∵l1∥l2,∴a∥b,
则==,
解得n=-4,m=6,
∴m+3n=6-12=-6.
2.【答案】C
【解析】以D为坐标原点,DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系(图略),
则D(0,0,0),A(1,0,0),B1(1,1,),D1(0,0,),
所以=(-1,0,),=(1,1,),
因为|cos〈,〉|===.
所以异面直线AD1与DB1所成角的余弦值为.
3.【答案】C
【解析】因为点A(1-t,1-t,t),B(2,t,t),
所以|AB|2=(1+t)2+(2t-1)2+(t-t)2=5t2-2t+2,
由二次函数易知,当t=时,取得最小值为,
所以|AB|的最小值为.
4.【答案】A
【解析】|cos〈m,n〉|===,
即〈m,n〉=60°.
∴两平面所成角为60°.
5.【答案】D
【解析】由题可知||=1,||=1,||=.
〈,〉=45°,〈,〉=45°,〈,〉=60°,
所以||2=2=2+2+2-·+·-·=++2-×1×1×+1××-1××=.
6.【答案】BC
【解析】由题意可知,B1G在底面上的射影为BG,而BC不垂直BG,则B1G不垂直于BC,则选项A不正确;
连接AD1和BC1,由E,F,G,H分别为CC1,BC,CD,BB1的中点,可知EF∥BC1∥AD1,则平面AEF∩平面AA1D1D=AD1,所以选项B正确;
由题知,可设正方体的棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,则各点坐标如下:A(2,0,0),E(0,2,1),A1(2,0,2),H(2,2,1),F(1,2,0),=(0,2,-1),=(-1,2,0),=(1,0,-1),=(0,0,2),设平面AEF的法向量为n=(x,y,z),则即令y=1,得x=2,z=2,得平面AEF的法向量为n=(2,1,2),所以·n=0,所以A1H∥平面AEF,则C选项正确;
由图可知,AA1⊥平面AFC,所以是平面AFC的法向量,则cos〈,n〉==.平面EAF与平面AFC的夹角的大小不是,所以D不正确.
7.【答案】A
【解析】分别以BC,BA,BD所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,设BD=a,
则A(0,1,0),B(0,0,0),E,D(0,0,a)
,
=(0,-1,a),=,
cosθ=
=
=,
解得a=2,
该四面体的体积为××1×1×2=.
8.【答案】A
【解析】如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则C1(0,3,1),D1(0,0,1),E(1,1,0),C(0,3,0),
所以=(0,3,1),=(1,1,-1),=(0,3,-1).
设平面D1EC的法向量为n=(x,y,z),
则
即即
取y=1,得n=(2,1,3).
因为cos〈,n〉===,
所以DC1与平面D1EC所成的角的正弦值为.
9.【答案】B
【解析】由△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,取AD中点G,建立如图所示的空间直角坐标系,
依题意G(0,0,0),A(1,0,0),D(-1,0,0),B(1,2,0),P(0,0,1),设F(1,y,0),
设=x=x(1,0,1)=(x,0,x),0
故|·|=||·||cos
30°,
即2=××,
即y2=-2(x-1)2+,0
又0
【解析】不妨设BC=1,AB=λ,则=λ,记=a,=b,=c,则=b-a,=c-b,根据题意,|a|=|c|=1,|b|=λ,a·b=b·c=c·a=0,所以·=-b2=-λ2,而||=,||=,所以|cos〈,〉|===,得λ=.
11.【答案】
【解析】建立如图所示的空间直角坐标系,
则D(0,0,0),A(1,-1,0),B(1,0,0),C(0,1,0),C1(0,1,2),
E,
∴=(0,1,2),=.
设平面EDC1的法向量为n=(x,y,z),
则
令z=1,则x=-,y=-2,
∴n=.
∴点B到平面EDC1的距离d===.
12.【答案】
【解析】建立如图所示的空间直角坐标系,
则A(1,0,0),C(0,1,0),
B(1,1,0),D1(0,0,1),
由=λ得P(λ,λ,1-λ),
则=(1-λ,-λ,λ-1),=(-λ,1-λ,λ-1),
因为∠APC为锐角,
所以·=(1-λ,-λ,λ-1)·(-λ,1-λ,λ-1)=(λ-1)(3λ-1)>0,
解得λ<或λ>1,
又因为动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,
所以λ的取值范围为0≤λ<.
13.【答案】4
【解析】以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设DD1=a,
则A(2,0,0),C(0,2,0),
D1(0,0,a),
故=(-2,2,0),=(-2,0,a),=(0,0,a),
设平面ACD1的一个法向量为n=(x,y,z),
则
可取n=,
故cos〈n,〉===,
又直线CC1与平面ACD1所成角的正弦值为,
∴=,
解得a=4.
14.【答案】
【解析】因为AE∶ED∶AD=1∶1∶,
所以AE⊥ED,即AE,DE,EF两两垂直,
所以建立如图所示的空间直角坐标系,
设AB=EF=CD=2,
则E(0,0,0),A(1,0,0),F(0,2,0),C(0,2,1),
所以=(-1,2,0),=(0,2,1),
所以cos〈,〉===,
所以AF与CE所成角的余弦值为.
15.【答案】(1)证明 ∵PA=AB,E为线段PB的中点,
∴AE⊥PB.
∵PA⊥底面ABCD,BC 平面ABCD,
∴PA⊥BC.
∵底面ABCD为正方形,
∴BC⊥AB.
又PA∩AB=A,PA,AB 平面PAB,
∴BC⊥平面PAB.
∵AE 平面PAB,
∴BC⊥AE.
∵PB∩BC=B,PB,BC 平面PBC,
∴AE⊥平面PBC.
∵EF 平面PBC,
∴AE⊥EF,
∴点F在线段BC上移动时,△AEF为直角三角形.
(2)解 如图,以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,连接DF,令PA=2,则A(0,0,0),B(2,0,0),E(1,0,1),F(2,1,0),D(0,2,0),
设平面AEF的法向量为m=(x,y,z),
则
可得取m=(1,-2,-1),
设平面DEF的法向量为n=(a,b,c),
则
可得取n=(1,2,3),
∴|cos〈m,n〉|==,
∴平面AEF与平面DEF夹角的余弦值为.
16.【答案】(1)证明 由已知可得AE=2,AD=1,∠A=60°.
从而DE==.
故AD2+DE2=AE2,
∴A1D⊥DE,BD⊥DE.
∴∠A1DB为二面角A1-DE-B的平面角.
又二面角A1-DE-B为直二面角,
∴∠A1DB=90°,
即A1D⊥DB.
∵DE∩DB=D,且DE,DB 平面BCED,
∴A1D⊥平面BCED.
(2)解 存在.
由(1)知ED⊥DB,A1D⊥平面BCED,以D为坐标原点,以射线DB,DE,DA1分别为x轴,y轴,z轴的正半轴建立空间直角坐标系,如图,
过P作PH∥DE交BD于点H,
设PB=2a(0≤2a≤3),
则BH=a,PH=a,DH=2-a,
易知A1(0,0,1),P(2-a,a,0),E(0,,0),
∴=(a-2,-a,1),
∵DE⊥平面A1BD,
∴平面A1BD的一个法向量为=(0,,0).
∵直线PA1与平面A1BD所成的角为60°,
∴sin
60°===,
解得a=.
∴PB=2a=,满足0≤2a≤3,符合题意.
∴在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°,此时PB=.
17.【答案】(1)证明 依题意,以点A为坐标原点建立空间直角坐标系(如图),可得A(0,0,0),B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得E(1,1,1),所以=(0,1,1),=(2,0,0),故·=0,所以BE⊥DC.
(2)解 =(1,2,0),=(-2,-2,2),=(2,2,0),=(1,0,0).
由点F在棱PC上,设=λ(0≤λ≤1),
故=+=+λ=(1-2λ,2-2λ,2λ).
由BF⊥AC,得·=0,
因此2(1-2λ)+2(2-2λ)=0,解得λ=,
即=.
设n1=(x,y,z)为平面FAB的法向量,
则
即
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.
易知向量n2=(0,1,0)为平面ABP的一个法向量,
则cos〈n1,n2〉===-.
所以平面FAB与平面ABP夹角的余弦值为.
(
第
12
页
共
13
页
)
同课章节目录
