沪教版(上海)高中数学高一下册 6.2 正切函数的图像与性质 课件1(共17张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 6.2 正切函数的图像与性质 课件1(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:30:22 | ||
图片预览




文档简介
(共17张PPT)
正切函数的图像与性质
1.
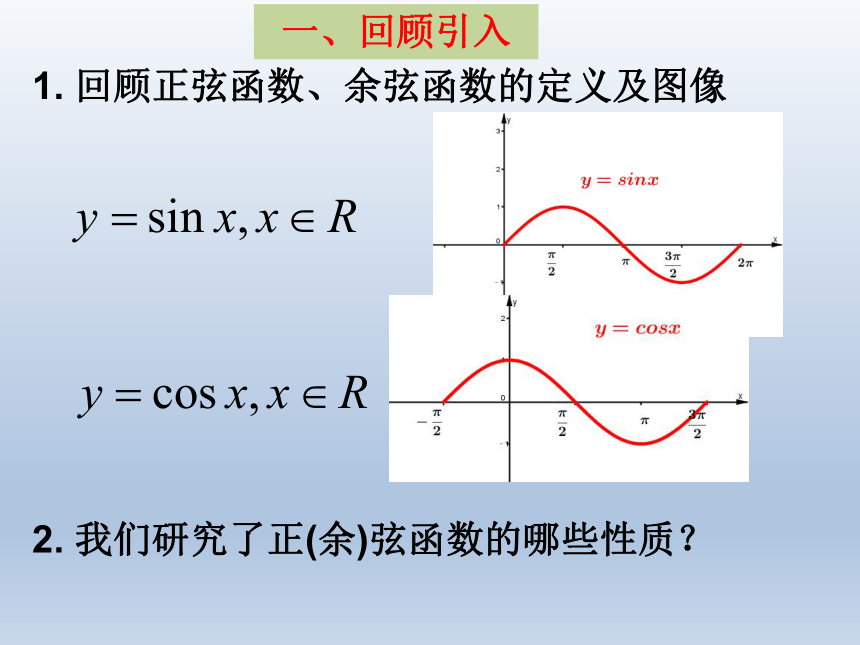
回顾正弦函数、余弦函数的定义及图像
一、回顾引入
2.
我们研究了正(余)弦函数的哪些性质?
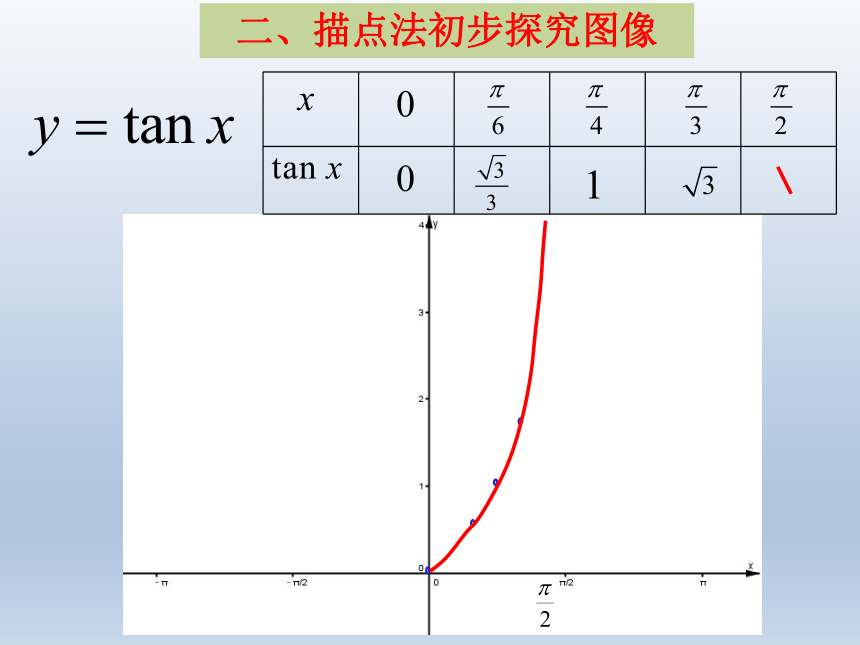
二、描点法初步探究图像
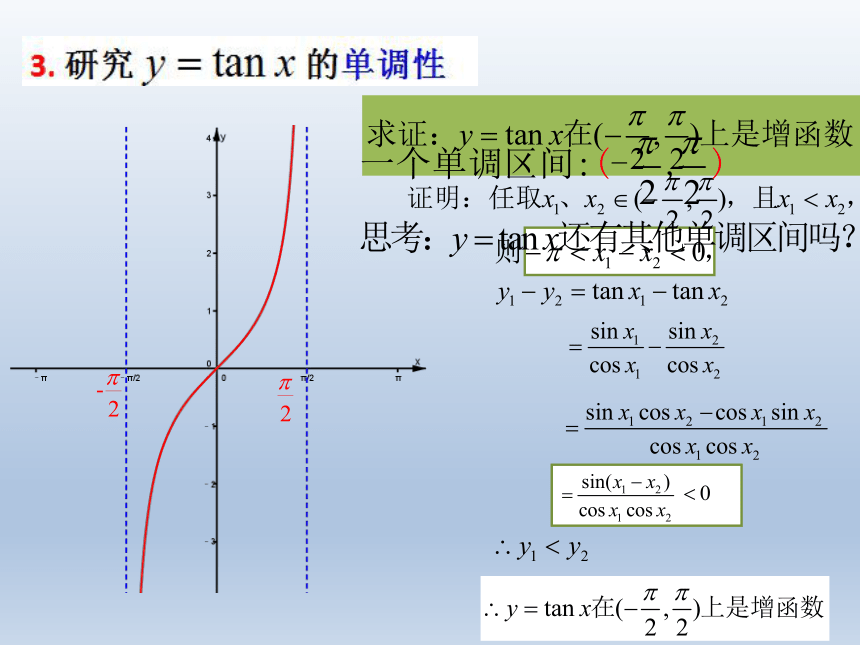
三、研究正切函数的性质与图像
渐近线
是奇函数
是奇函数
A
B
渐近线
渐近线
渐近线
渐近线
渐近线
渐近线
定义域
值域
周期性
奇偶性
单调性
渐近线
R
T=
奇函数
四、结合图像,归纳性质
对称中心:
对称中心:
对称中心:
解:
(1)定义域:
(2)周期:
(3)单调区间:
例1、求函数
的定义域、周期和单调区间
五、例题分析
拓展练习、求函数
的定义域、周期和单调区间
六、课堂小结
定义域
值域
周期性
奇偶性
单调性
渐近线
对称中心
R
T=
奇函数
增区间
性质决定图像;
图像凸显性质。
5T2
2nT
BIT/2
31r/22
2TT
3iT
3
5丌
T
2丌
21
2
求证:f(x)=4tm(aox+o)周期是x
证明:当O>0时,f(x)=Atan(ax+q)=Atan(x+q+x)
A
tan
o(x+-)+o=f(x+-)
当<0时,f(x)=Atan(omx+q)=Atan(ax+q-x)
A
tan
a(x-)o=flx+c-l
T
正切函数的图像与性质
1.
回顾正弦函数、余弦函数的定义及图像
一、回顾引入
2.
我们研究了正(余)弦函数的哪些性质?
二、描点法初步探究图像
三、研究正切函数的性质与图像
渐近线
是奇函数
是奇函数
A
B
渐近线
渐近线
渐近线
渐近线
渐近线
渐近线
定义域
值域
周期性
奇偶性
单调性
渐近线
R
T=
奇函数
四、结合图像,归纳性质
对称中心:
对称中心:
对称中心:
解:
(1)定义域:
(2)周期:
(3)单调区间:
例1、求函数
的定义域、周期和单调区间
五、例题分析
拓展练习、求函数
的定义域、周期和单调区间
六、课堂小结
定义域
值域
周期性
奇偶性
单调性
渐近线
对称中心
R
T=
奇函数
增区间
性质决定图像;
图像凸显性质。
5T2
2nT
BIT/2
31r/22
2TT
3iT
3
5丌
T
2丌
21
2
求证:f(x)=4tm(aox+o)周期是x
证明:当O>0时,f(x)=Atan(ax+q)=Atan(x+q+x)
A
tan
o(x+-)+o=f(x+-)
当<0时,f(x)=Atan(omx+q)=Atan(ax+q-x)
A
tan
a(x-)o=flx+c-l
T
