沪教版(上海)高中数学高一下册 6.1 三角函数 复习课件(共48张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 6.1 三角函数 复习课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 00:00:00 | ||
图片预览










文档简介
(共48张PPT)
第6章
三角函数
复习课件
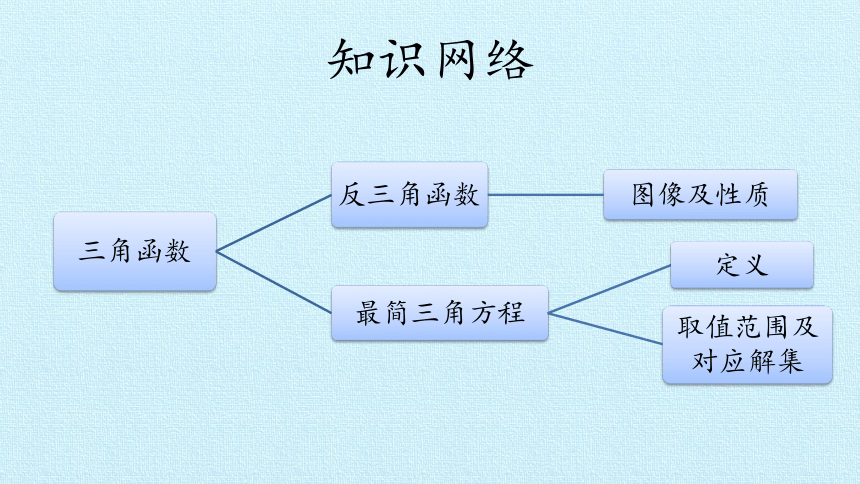
知识网络
知识网络
1.任意角三角函数的定义
在平面直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的
,记作
,即
;
(2)x叫做α的
,记作
,即
;
(3)
叫做α的
,记作
,即
.
tan
α
正弦
sin
α
sin
α=y
余弦
cos
α
cos
α=x
正切
知识梳理
2.正弦函数、余弦函数和正切函数的性质
函数
y=sin
x
y=cos
x
y=tan
x
图象
定义域
R
R
{x|x∈R且x≠
kπ+
,k∈Z}
值域
________
________
__
对称性
对称轴:x=kπ+
(k∈Z);
对称中心:(kπ,0)(k∈Z)
对称轴:x=kπ(k∈Z);
对称中心:
(k∈Z)
对称中心:
(k∈Z),
无对称轴
奇偶性
_______
_______
_______
周期性
最小正周期:___
最小正周期:___
最小正周期:__
[-1,1]
[-1,1]
R
奇函数
偶函数
奇函数
2π
2π
π
单
调
性
在
(k∈Z)上是增加的;在
(k∈Z)上是减少的
在[-π+2kπ,2kπ](k∈Z)
上是增加的;在[2kπ,π+2kπ]
(k∈Z)上是减少的
在开区间(kπ-
,kπ+
)
(k∈Z)上是增加的
最值
在x=
(k∈Z)时,ymax=1;在x=-
+2kπ
(k∈Z)时,ymin=-1
在x=2kπ(k∈Z)时,ymax=1;在x=π+2kπ(k∈Z)时,ymin=-1
无最值
3.反三角函数
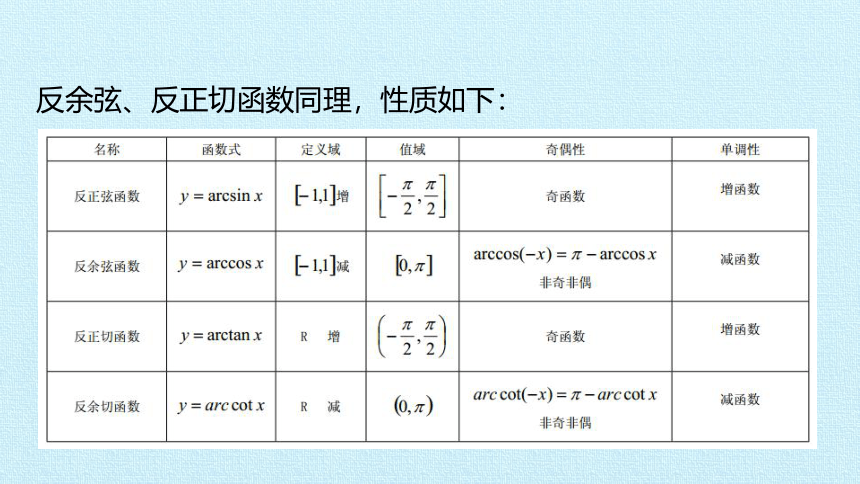
反余弦、反正切函数同理,性质如下:
4.最简单的三角方程
例1 已知角θ的顶点为坐标原点,始边为x轴的正半轴.若P(4,y)是角θ终边上一点,且sin
θ=-
,则y=
.
答案
解析
-8
类型一 三角函数的概念
所以θ为第四象限角,解得y=-8.
反思与感悟
(1)已知角α的终边在直线上时,常用的解题方法有以下两种:
①先利用直线与单位圆相交,求出交点坐标,然后再利用正弦、余弦函数的定义求出相应三角函数值。
②在α的终边上任选一点P(x,y),P到原点的距离为r(r>0).则sinα=
,cosα=
.已知α的终边求α的三角函数值时,用这几个公式更方便。
(2)当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行分类讨论。
跟踪训练1 已知角α的终边上有一点P(24k,7k),k≠0,求sin
α,cos
α,tan
α的值.
解答
解 当k>0时,令x=24k,y=7k,
当k<0时,令x=24k,y=7k,则有r=-25k,
类型二 三角函数的图像与性质
解答
例2 将函数y=f(x)的图像向左平移1个单位长度,纵坐标不变,横坐标缩短到原来的
倍,然后向上平移1个单位长度,得到函数y=
sin
x的图像。
(1)求f(x)的最小正周期和递增区间;
(2)若函数y=g(x)与y=f(x)的图像关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最小值和最大值。
解 ∵函数y=g(x)与y=f(x)的图像关于直线x=2对称,
∴当x∈[0,1]时,y=g(x)的最值即为x∈[3,4]时,y=f(x)的最值。
解答
反思与感悟
研究y=Asin(ωx+φ)的单调性、最值问题,把ωx+φ看作一个整体来解决。
跟踪训练2 函数f(x)=3sin
的部分图像如图所示:
(1)写出f(x)的最小正周期及图中x0,y0的值;
解答
解答
类型三 三角函数的最值和值域
解答
命题角度1 可化为y=Asin(ωx+φ)+k型
例3 求函数y=-2sin(x+
)+3,x∈[0,π]的最大值和最小值。
反思与感悟
利用y=Asin(ωx+φ)+k求值域时要注意角的取值范围对函数式取值的影响。
解答
∴a,b的取值分别是4,-3或-4,-1.
求a,b的值。
命题角度2 可化为sin
x或cos
x的二次函数型
例4 已知|x|≤
,求函数f(x)=cos2x+sin
x的最小值。
解答
解 y=f(x)=cos2x+sin
x=-sin2x+sin
x+1.
反思与感悟
在换元时要立刻写出新元的范围,否则极易出错。
解答
跟踪训练4 已知函数f(x)=-sin2x-asin
x+b+1的最大值为0,最小值为-4,若实数a>0,求a,b的值。
解 令t=sin
x,则
综上所述,a=2,b=-2.
命题角度3 分式型函数利用有界性求值域
例5 求函数y=
的值域。
解答
∵|cos
x|≤1,∴-3≤2cos
x-1≤1且2cos
x-1≠0,
反思与感悟
在三角函数中,正弦函数和余弦函数有一个重要的特征——有界性,利用三角函数的有界性可以求解三角函数的值域问题。
跟踪训练5 求函数y=
的最大值和最小值。
解答
例6
求函数y=3x-2的反函数,并画出原函数和反函数的图像.
解
∵y=3x-2
∴函数y=3x-2(x∈R)
的反函数为
y=
∴x=
1
-2
-1
1
-1
-2
x
y
y=3x-2
x∈R
类型四 反三角函数与最简三角方程
解答
例7
反思与感悟
由于三角函数的周期性,可以在一个给定的单点区间内研究其反函数——反三角函数。
解最简单的三角方程是解简单的三角方程的基础,要在理解三角方程的基础上,熟练地写出最简单的三角方程的解;要熟悉同名三角函数相等时角度之间的关系在解三角方程中的作用。
跟踪训练6
(3)已知
,求
解:
因此
解法二:设
因此
即点
在
图像上
即点
在
图像上
解得
解毕
类型五 数形结合思想在三角函数中的应用
解答
反思与感悟
数形结合思想贯穿了三角函数的始终,对于与方程解有关的问题以及在研究y=Asin(ωx+φ)(A>0,ω>0)的性质和由性质研究图像时,常利用数形结合思想。
可作出示意图如图所示(一种情况),
答案
解析
跟踪训练7 设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0).若f(x)在区间
上具有单调性,且
,则f(x)的最小正周期为
.
π
当堂训练
1.若一个α角的终边上有一点P(-4,a),且sin
α·cos
α=
,则a的值为
答案
解析
√
1
2
3
4
5
1
2
3
4
5
答案
解析
√
=-cos
α,
1
2
3
4
5
3.函数y=|sin
x|+sin|x|的值域为
A.[-2,2]
B.[-1,1]
C.[0,2]
D.[0,1]
答案
解析
∴0≤f(x)≤2.故选C.
√
答案
解析
1
2
3
4
5
4.函数f(x)=2sin(ωx+φ)
的部分图像如图所示,则ω,φ的值分别是
√
1
2
3
4
5
5.已知函数f(x)=-sin2x+sin
x+a,若1≤f(x)≤
对一切x∈R恒成立,求实数a的取值范围.
解答
1
2
3
4
5
解 令t=sin
x,则t∈[-1,1],
当t=-1时,f(t)min=a-2,即f(x)min=a-2.
故实数a的取值范围为[3,4].
1
2
3
4
5
三角函数的性质是本章复习的重点,在复习时,要充分利用数形结合思想把图像与性质结合起来,即利用图像的直观性得到函数的性质,或由单位圆中三角函数线表示的三角函数值来获得函数的性质,同时也能利用函数的性质来描述函数的图像,这样既有利于掌握函数的图像与性质,又能熟练运用数形结合的思想方法。
规律与方法
谢
谢
第6章
三角函数
复习课件
知识网络
知识网络
1.任意角三角函数的定义
在平面直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的
,记作
,即
;
(2)x叫做α的
,记作
,即
;
(3)
叫做α的
,记作
,即
.
tan
α
正弦
sin
α
sin
α=y
余弦
cos
α
cos
α=x
正切
知识梳理
2.正弦函数、余弦函数和正切函数的性质
函数
y=sin
x
y=cos
x
y=tan
x
图象
定义域
R
R
{x|x∈R且x≠
kπ+
,k∈Z}
值域
________
________
__
对称性
对称轴:x=kπ+
(k∈Z);
对称中心:(kπ,0)(k∈Z)
对称轴:x=kπ(k∈Z);
对称中心:
(k∈Z)
对称中心:
(k∈Z),
无对称轴
奇偶性
_______
_______
_______
周期性
最小正周期:___
最小正周期:___
最小正周期:__
[-1,1]
[-1,1]
R
奇函数
偶函数
奇函数
2π
2π
π
单
调
性
在
(k∈Z)上是增加的;在
(k∈Z)上是减少的
在[-π+2kπ,2kπ](k∈Z)
上是增加的;在[2kπ,π+2kπ]
(k∈Z)上是减少的
在开区间(kπ-
,kπ+
)
(k∈Z)上是增加的
最值
在x=
(k∈Z)时,ymax=1;在x=-
+2kπ
(k∈Z)时,ymin=-1
在x=2kπ(k∈Z)时,ymax=1;在x=π+2kπ(k∈Z)时,ymin=-1
无最值
3.反三角函数
反余弦、反正切函数同理,性质如下:
4.最简单的三角方程
例1 已知角θ的顶点为坐标原点,始边为x轴的正半轴.若P(4,y)是角θ终边上一点,且sin
θ=-
,则y=
.
答案
解析
-8
类型一 三角函数的概念
所以θ为第四象限角,解得y=-8.
反思与感悟
(1)已知角α的终边在直线上时,常用的解题方法有以下两种:
①先利用直线与单位圆相交,求出交点坐标,然后再利用正弦、余弦函数的定义求出相应三角函数值。
②在α的终边上任选一点P(x,y),P到原点的距离为r(r>0).则sinα=
,cosα=
.已知α的终边求α的三角函数值时,用这几个公式更方便。
(2)当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行分类讨论。
跟踪训练1 已知角α的终边上有一点P(24k,7k),k≠0,求sin
α,cos
α,tan
α的值.
解答
解 当k>0时,令x=24k,y=7k,
当k<0时,令x=24k,y=7k,则有r=-25k,
类型二 三角函数的图像与性质
解答
例2 将函数y=f(x)的图像向左平移1个单位长度,纵坐标不变,横坐标缩短到原来的
倍,然后向上平移1个单位长度,得到函数y=
sin
x的图像。
(1)求f(x)的最小正周期和递增区间;
(2)若函数y=g(x)与y=f(x)的图像关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最小值和最大值。
解 ∵函数y=g(x)与y=f(x)的图像关于直线x=2对称,
∴当x∈[0,1]时,y=g(x)的最值即为x∈[3,4]时,y=f(x)的最值。
解答
反思与感悟
研究y=Asin(ωx+φ)的单调性、最值问题,把ωx+φ看作一个整体来解决。
跟踪训练2 函数f(x)=3sin
的部分图像如图所示:
(1)写出f(x)的最小正周期及图中x0,y0的值;
解答
解答
类型三 三角函数的最值和值域
解答
命题角度1 可化为y=Asin(ωx+φ)+k型
例3 求函数y=-2sin(x+
)+3,x∈[0,π]的最大值和最小值。
反思与感悟
利用y=Asin(ωx+φ)+k求值域时要注意角的取值范围对函数式取值的影响。
解答
∴a,b的取值分别是4,-3或-4,-1.
求a,b的值。
命题角度2 可化为sin
x或cos
x的二次函数型
例4 已知|x|≤
,求函数f(x)=cos2x+sin
x的最小值。
解答
解 y=f(x)=cos2x+sin
x=-sin2x+sin
x+1.
反思与感悟
在换元时要立刻写出新元的范围,否则极易出错。
解答
跟踪训练4 已知函数f(x)=-sin2x-asin
x+b+1的最大值为0,最小值为-4,若实数a>0,求a,b的值。
解 令t=sin
x,则
综上所述,a=2,b=-2.
命题角度3 分式型函数利用有界性求值域
例5 求函数y=
的值域。
解答
∵|cos
x|≤1,∴-3≤2cos
x-1≤1且2cos
x-1≠0,
反思与感悟
在三角函数中,正弦函数和余弦函数有一个重要的特征——有界性,利用三角函数的有界性可以求解三角函数的值域问题。
跟踪训练5 求函数y=
的最大值和最小值。
解答
例6
求函数y=3x-2的反函数,并画出原函数和反函数的图像.
解
∵y=3x-2
∴函数y=3x-2(x∈R)
的反函数为
y=
∴x=
1
-2
-1
1
-1
-2
x
y
y=3x-2
x∈R
类型四 反三角函数与最简三角方程
解答
例7
反思与感悟
由于三角函数的周期性,可以在一个给定的单点区间内研究其反函数——反三角函数。
解最简单的三角方程是解简单的三角方程的基础,要在理解三角方程的基础上,熟练地写出最简单的三角方程的解;要熟悉同名三角函数相等时角度之间的关系在解三角方程中的作用。
跟踪训练6
(3)已知
,求
解:
因此
解法二:设
因此
即点
在
图像上
即点
在
图像上
解得
解毕
类型五 数形结合思想在三角函数中的应用
解答
反思与感悟
数形结合思想贯穿了三角函数的始终,对于与方程解有关的问题以及在研究y=Asin(ωx+φ)(A>0,ω>0)的性质和由性质研究图像时,常利用数形结合思想。
可作出示意图如图所示(一种情况),
答案
解析
跟踪训练7 设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0).若f(x)在区间
上具有单调性,且
,则f(x)的最小正周期为
.
π
当堂训练
1.若一个α角的终边上有一点P(-4,a),且sin
α·cos
α=
,则a的值为
答案
解析
√
1
2
3
4
5
1
2
3
4
5
答案
解析
√
=-cos
α,
1
2
3
4
5
3.函数y=|sin
x|+sin|x|的值域为
A.[-2,2]
B.[-1,1]
C.[0,2]
D.[0,1]
答案
解析
∴0≤f(x)≤2.故选C.
√
答案
解析
1
2
3
4
5
4.函数f(x)=2sin(ωx+φ)
的部分图像如图所示,则ω,φ的值分别是
√
1
2
3
4
5
5.已知函数f(x)=-sin2x+sin
x+a,若1≤f(x)≤
对一切x∈R恒成立,求实数a的取值范围.
解答
1
2
3
4
5
解 令t=sin
x,则t∈[-1,1],
当t=-1时,f(t)min=a-2,即f(x)min=a-2.
故实数a的取值范围为[3,4].
1
2
3
4
5
三角函数的性质是本章复习的重点,在复习时,要充分利用数形结合思想把图像与性质结合起来,即利用图像的直观性得到函数的性质,或由单位圆中三角函数线表示的三角函数值来获得函数的性质,同时也能利用函数的性质来描述函数的图像,这样既有利于掌握函数的图像与性质,又能熟练运用数形结合的思想方法。
规律与方法
谢
谢
