沪教版(上海)高中数学高一下册 4.6 对数函数 课件26(共38张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 4.6 对数函数 课件26(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:30:06 | ||
图片预览










文档简介
(共38张PPT)
对数与对数函数
1.对数的概念
如果ax=N(a>0且a≠1),那么x叫做以a为底N的对数,记作____________.
2.对数的性质、换底公式与运算性质
x=logaN
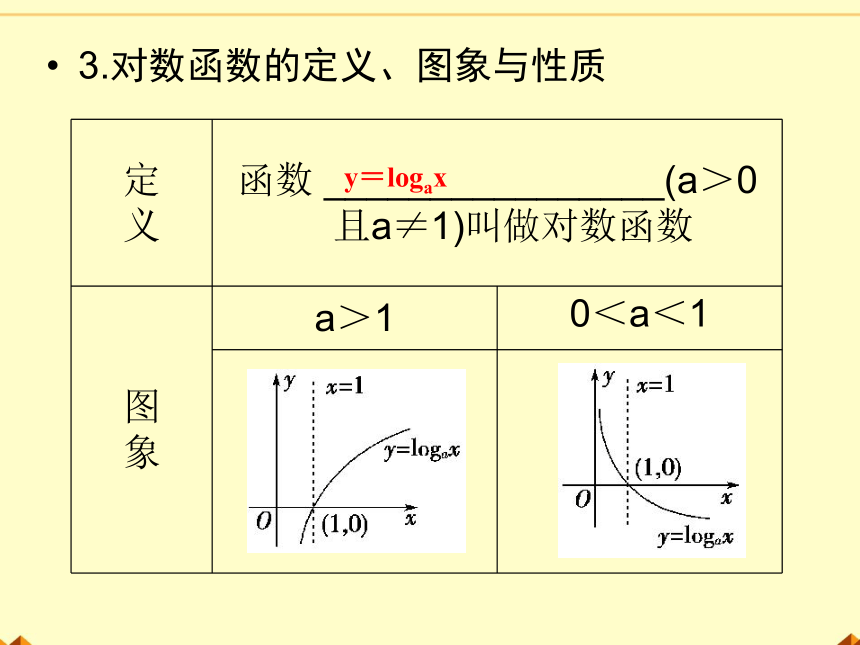
3.对数函数的定义、图象与性质
定
义
函数
________________(a>0且a≠1)叫做对数函数
图
象
a>1
0<a<1
y=logax
性
质
定义域:_____________
值域:_______________
当x=1时,y=0,即过定点_________
当0<x<1时,y<0;
当x>1时,__________.
当0<x<1时,y>0;当x>1时,________.
在(0,+∞)上为___________
在(0,+∞)上为___________
(0,+∞)
(-∞,+∞)
(1,0)
y>0
y<0
增函数
减函数
4.反函数
指数函数y=ax(a>0且a≠1)与对数函数
____________(a>0且a≠1)互为反函数,它们的图象关于直线_______对称.
y=logax
y=x
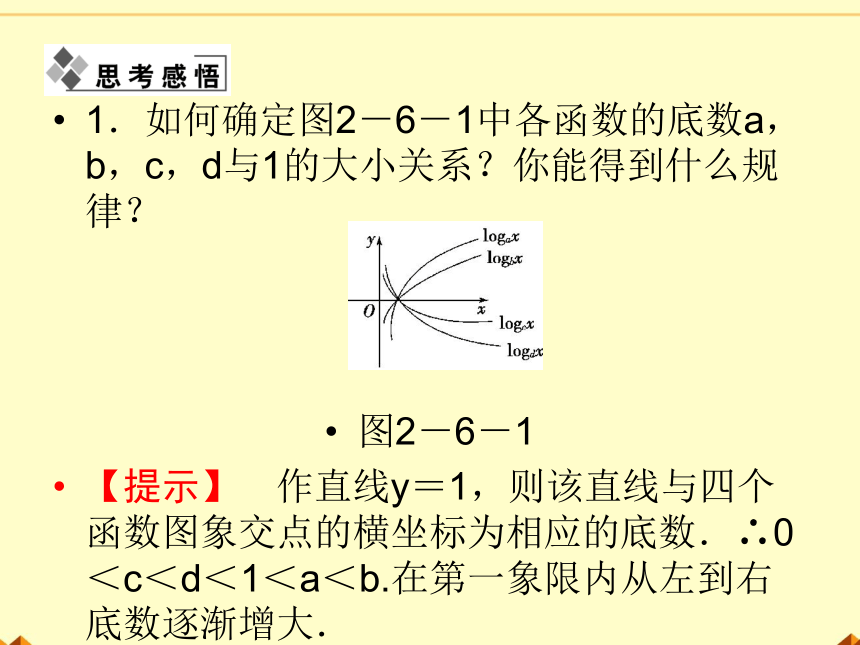
1.如何确定图2-6-1中各函数的底数a,b,c,d与1的大小关系?你能得到什么规律?
图2-6-1
【提示】 作直线y=1,则该直线与四个函数图象交点的横坐标为相应的底数.∴0<c<d<1<a<b.在第一象限内从左到右底数逐渐增大.
2.当对数logab的值为正数或负数时,a,b满足什么条件?
【提示】 若logab>0,则a,b∈(1,+∞)或a,b∈(0,1).
若logab<0,则a∈(1,+∞)且b∈(0,1)或a∈(0,1)且b∈(1,+∞).
1.(人教A版教材习题改编)2log510+log50.25=( )
A.0
B.1
C.2
D.4
【解析】 2log510+log50.25=log5100+log50.25=2.
【答案】 C
【解析】 由题意知f(x)=logax,又f(2)=1,
∴loga2=1,a=2.
∴f(x)=log2x.
【答案】 D
【答案】 D
4.(2012·北京高考)已知函数f(x)=lg
x,若f(ab)=1,则f(a2)+f(b2)=________.
【解析】 ∵f(x)=lg
x,
∴f(a2)+f(b2)=2lg
a+2lg
b=2lg
ab.
又f(ab)=1,∴lg
ab=1,∴f(a2)+f(b2)=2.
【答案】 2
【思路点拨】 (1)根据乘法公式和对数运算性质进行计算;
(2)利用换底公式化为同底的对数,再进行计算.
1.对数运算法则是在化为同底的情况下进行的,因此经常用到换底公式及其推论;在对含字母的对数式化简时必须保证恒等变形.
2.ab=N?b=logaN(a>0且a≠1)是解决有关指数、对数问题的有效方法,在运算中要注意互化.
3.利用对数运算法则,在积、商、幂的对数与对数的和、差、倍之间进行转化.
(2)作出f(x)的大致图象.不妨设a<b<c,因为a、b、c互不相等,且f(a)=f(b)=f(c),由函数的图象可知10<c<12.
∵|lg
a|=|lg
b|,且a≠b,
所以lg
a=-lg
b,可得ab=1,所以abc=c∈(10,12).
【答案】 (1)D (2)C
1.解答本题(1)时,可假设一个图象正确,然后看另一个图象是否符合要求;对于本题(2)根据|lg
a|=|lg
b|得到ab=1是解题的关键.
2.对一些可通过平移、对称变换能作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合求解.
3.一些对数型方程、不等式问题的求解,常转化为相应函数图象问题,利用数形结合法求解.
(1)已知函数f(x)=ln
x,g(x)=lg
x,h(x)=log3x,直线y=a(a<0)与这三个函数的交点的横坐标分别是x1,x2,x3,则x1,x2,x3的大小关系是( )
A.x2<x3<x1
B.x1<x3<x2
C.x1<x2<x3
D.x3<x2<x1
(2)函数y=log2|x+1|的单调递减区间为________,单调递增区间为________.
【解析】 (1)在同一坐标系中画出三个函数的图象及直线y=a(a<0),易知x1>x3>x2.
(2)作出函数y=log2x的图象,将其关于y轴对称得到函数y=log2|x|的图象,再将图象向左平移1个单位长度就得到函数y=log2|x+1|的图象(如图所示).
由图知,函数y=log2|x+1|的递减区间为(-∞,-1),递增区间为(-1,+∞).
【答案】 (1)A (2)(-∞,-1) (-1,+∞)
【思路点拨】 (1)利用真数大于0构建不等式,但要注意分类讨论.
(2)先由条件求出a的值,再讨论奇偶性和单调性.
1.利用对数函数的性质比较对数值大小:
(1)同底数(或能化为同底的)可利用函数单调性处理;
(2)底数不同,真数相同的对数值的比较,可利用函数图象或比较其倒数大小来进行.
(3)既不同底数,又不同真数的对数值的比较,先引入中间量(如-1,0,1等),再利用对数函数性质进行比较.
2.利用对数函数性质研究对数型函数性质,要注意三点,一是定义域;二是底数与1的大小关系;三是复合函数的构成.
(2013·中山模拟)已知函数f(x)=loga(8-ax)(a>0,a≠1),若f(x)>1在区间[1,2]上恒成立,求实数a的取值范围.
【答案】 B
【答案】 C
对数与对数函数
1.对数的概念
如果ax=N(a>0且a≠1),那么x叫做以a为底N的对数,记作____________.
2.对数的性质、换底公式与运算性质
x=logaN
3.对数函数的定义、图象与性质
定
义
函数
________________(a>0且a≠1)叫做对数函数
图
象
a>1
0<a<1
y=logax
性
质
定义域:_____________
值域:_______________
当x=1时,y=0,即过定点_________
当0<x<1时,y<0;
当x>1时,__________.
当0<x<1时,y>0;当x>1时,________.
在(0,+∞)上为___________
在(0,+∞)上为___________
(0,+∞)
(-∞,+∞)
(1,0)
y>0
y<0
增函数
减函数
4.反函数
指数函数y=ax(a>0且a≠1)与对数函数
____________(a>0且a≠1)互为反函数,它们的图象关于直线_______对称.
y=logax
y=x
1.如何确定图2-6-1中各函数的底数a,b,c,d与1的大小关系?你能得到什么规律?
图2-6-1
【提示】 作直线y=1,则该直线与四个函数图象交点的横坐标为相应的底数.∴0<c<d<1<a<b.在第一象限内从左到右底数逐渐增大.
2.当对数logab的值为正数或负数时,a,b满足什么条件?
【提示】 若logab>0,则a,b∈(1,+∞)或a,b∈(0,1).
若logab<0,则a∈(1,+∞)且b∈(0,1)或a∈(0,1)且b∈(1,+∞).
1.(人教A版教材习题改编)2log510+log50.25=( )
A.0
B.1
C.2
D.4
【解析】 2log510+log50.25=log5100+log50.25=2.
【答案】 C
【解析】 由题意知f(x)=logax,又f(2)=1,
∴loga2=1,a=2.
∴f(x)=log2x.
【答案】 D
【答案】 D
4.(2012·北京高考)已知函数f(x)=lg
x,若f(ab)=1,则f(a2)+f(b2)=________.
【解析】 ∵f(x)=lg
x,
∴f(a2)+f(b2)=2lg
a+2lg
b=2lg
ab.
又f(ab)=1,∴lg
ab=1,∴f(a2)+f(b2)=2.
【答案】 2
【思路点拨】 (1)根据乘法公式和对数运算性质进行计算;
(2)利用换底公式化为同底的对数,再进行计算.
1.对数运算法则是在化为同底的情况下进行的,因此经常用到换底公式及其推论;在对含字母的对数式化简时必须保证恒等变形.
2.ab=N?b=logaN(a>0且a≠1)是解决有关指数、对数问题的有效方法,在运算中要注意互化.
3.利用对数运算法则,在积、商、幂的对数与对数的和、差、倍之间进行转化.
(2)作出f(x)的大致图象.不妨设a<b<c,因为a、b、c互不相等,且f(a)=f(b)=f(c),由函数的图象可知10<c<12.
∵|lg
a|=|lg
b|,且a≠b,
所以lg
a=-lg
b,可得ab=1,所以abc=c∈(10,12).
【答案】 (1)D (2)C
1.解答本题(1)时,可假设一个图象正确,然后看另一个图象是否符合要求;对于本题(2)根据|lg
a|=|lg
b|得到ab=1是解题的关键.
2.对一些可通过平移、对称变换能作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合求解.
3.一些对数型方程、不等式问题的求解,常转化为相应函数图象问题,利用数形结合法求解.
(1)已知函数f(x)=ln
x,g(x)=lg
x,h(x)=log3x,直线y=a(a<0)与这三个函数的交点的横坐标分别是x1,x2,x3,则x1,x2,x3的大小关系是( )
A.x2<x3<x1
B.x1<x3<x2
C.x1<x2<x3
D.x3<x2<x1
(2)函数y=log2|x+1|的单调递减区间为________,单调递增区间为________.
【解析】 (1)在同一坐标系中画出三个函数的图象及直线y=a(a<0),易知x1>x3>x2.
(2)作出函数y=log2x的图象,将其关于y轴对称得到函数y=log2|x|的图象,再将图象向左平移1个单位长度就得到函数y=log2|x+1|的图象(如图所示).
由图知,函数y=log2|x+1|的递减区间为(-∞,-1),递增区间为(-1,+∞).
【答案】 (1)A (2)(-∞,-1) (-1,+∞)
【思路点拨】 (1)利用真数大于0构建不等式,但要注意分类讨论.
(2)先由条件求出a的值,再讨论奇偶性和单调性.
1.利用对数函数的性质比较对数值大小:
(1)同底数(或能化为同底的)可利用函数单调性处理;
(2)底数不同,真数相同的对数值的比较,可利用函数图象或比较其倒数大小来进行.
(3)既不同底数,又不同真数的对数值的比较,先引入中间量(如-1,0,1等),再利用对数函数性质进行比较.
2.利用对数函数性质研究对数型函数性质,要注意三点,一是定义域;二是底数与1的大小关系;三是复合函数的构成.
(2013·中山模拟)已知函数f(x)=loga(8-ax)(a>0,a≠1),若f(x)>1在区间[1,2]上恒成立,求实数a的取值范围.
【答案】 B
【答案】 C
