沪教版(上海)高中数学高一下册 4.6 对数函数 课件37(共27张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 4.6 对数函数 课件37(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:29:00 | ||
图片预览







文档简介
(共27张PPT)
基本初等函数、导数及其应用
函数与方程
1.函数的零点
(1)函数零点的定义
函数的零点是什么?零点是点吗?
提示:对于函数y=f(x)(x∈R),我们把使f(x)=0的实数x,叫做函数的零点,函数的零点不是点,是方程f(x)=0的根,是函数y=f(x)的图象与x轴的交点的横坐标,它是一个实数
(2)几个等价关系
方程f(x)=0有实数根 函数y=f(x)的图象与______有
交
点 函数y=f(x)有______.
(3)函数零点的判定(零点存在性定理)
如果函数y=f(x)在区间[a,b]上的图象是连续不
断的一
条
曲线,并且有____________,那么函数y=f(x)在区间________内有零点,即存在c∈(a,b),使得________,这个c
也
就
是f(x)=0的根.
x轴
零点
f(a)·f(b)<0
(a,b)
f(c)=0
温馨提醒:(1)函数f(x)的零点是一个实数,是
方
程f(x)=0
的根,也是函数y=f(x)的图象与x轴交点的横坐标.
(2)函数零点存在性定理是零点存在的一个充分条件,而
不是必要条件;判断零点个数还要根据函数的单调性、对称
性
或结合函数图象.
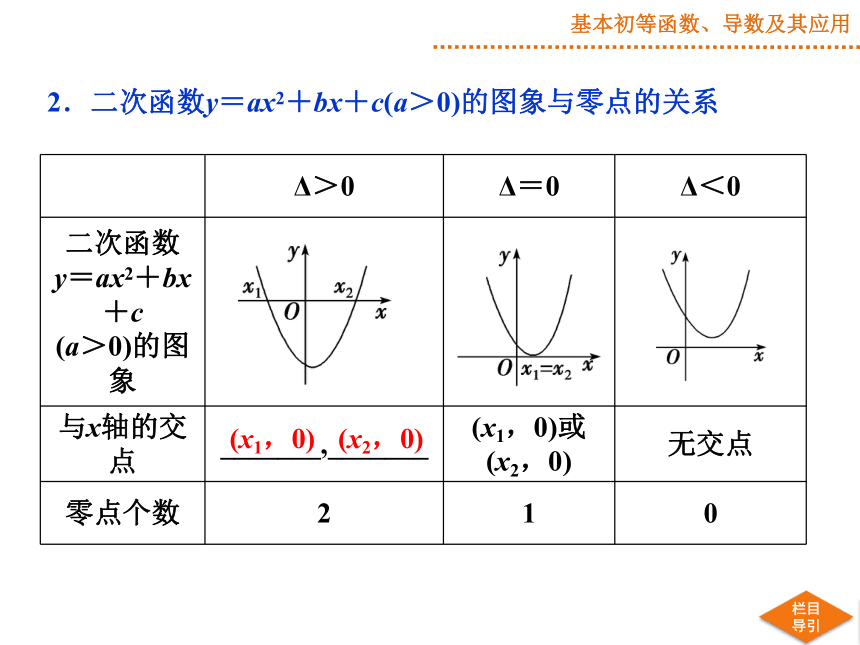
2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系
Δ>0
Δ=0
Δ<0
二次函数
y=ax2+bx+c
(a>0)的图象
与x轴的交点
_______,_______
(x1,0)或
(x2,0)
无交点
零点个数
2
1
0
(x1,0)
(x2,0)
3.二分法的定义
对于在区间[a,b]上连续不断且________________的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近______,进而得到零点近似值的方法叫
做
二分法.
温馨提醒:二分法是求方程的根的近似值的一种计算方法.其实质是通过不断地“取中点”来逐步缩小零点所在的范围,当达到一定的精确度要求时,所得区间的任一点就是这个函数零点的近似值.
f(a)·f(b)<0
零点
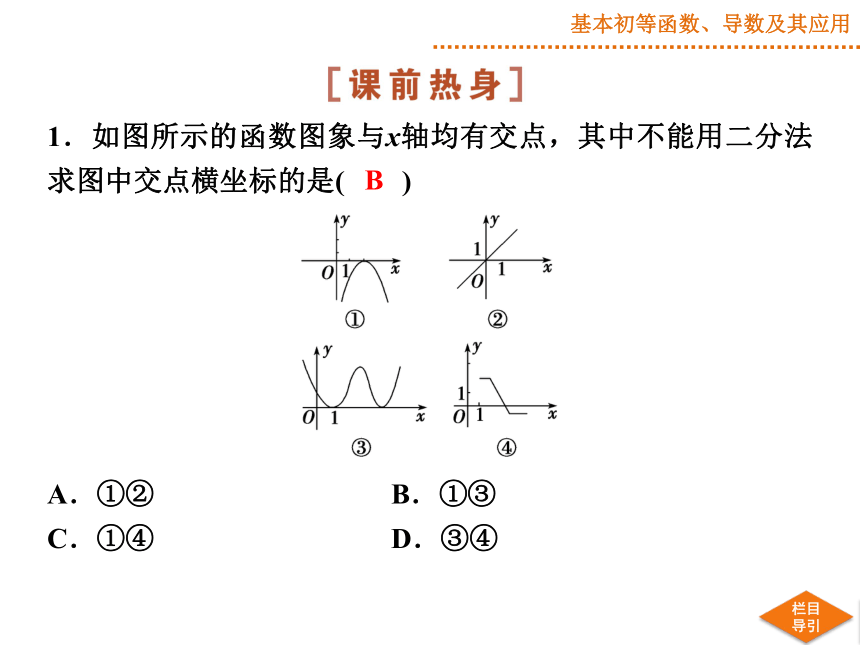
1.如图所示的函数图象与x轴均有交点,其中不能用二分法求图中交点横坐标的是( )
A.①②
B.①③
C.①④
D.③④
B
2.(2012·高考湖北卷改编)函数f(x)=xcos
x在
区间[0,2π]
上的零点的个数为( )
A.2
B.3
C.4
D.5
3.函数f(x)=2x+3x的零点所在的一个区间是( )
A.(-2,-1)
B.(-1,0)
C.(0,1)
D.(1,2)
4.函数y=|x|-cos
x在(-∞,+∞)内有________个零点.
5.已知函数f(x)=x2+x+a(a<0)在区间(0,1)上有零点,则a的取值范围为____________.
B
B
两
(-2,0)
函数零点所在区间的确定
[课堂笔记]
A
判断函数在某个区间上是否存在零点,要根据具体题目灵活处理.当能直接求出零点时,就直接求出进行判断;当不能直接求出时,可根据零点存在性定理判断;当用零点存在性定理也无法判断时可画出图象判断.
C
确定函数零点个数
D
(2)(2014·河北石家庄市模拟考试)[x]表示不超过x的最大整数,例如[2.9]=2,[-4.1]=-5,已知f(x)=x-[x](x∈R),g(x)=log4(x-1),则函数h(x)=f(x)-g(x)的零点个数是( )
A.1
B.2
C.3
D.4
[课堂笔记]
B
判断函数零点个数的方法:
(1)解方程法:令f(x)=0,如果能求出解,则有几个解就有
几个零点;
(2)零点存在性定理法:利用定理不仅要求函数在区
间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合
函数
的
图象与性质(如单调性、奇偶性、周期性、对称性)才能
确
定
函数有多少个零点或零点值所具有的性质;
(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的横
坐
标有几个不同的值,就有几个不同的零点.
C
A
函数零点的综合问题
[课堂笔记]
(0,1)
转化与化归思想在研究函数零点中的应用
B
已知a,b,c∈R,a+b+c=0,a+bc-1=0,则a的取值范
围是_____________________________________.
基本初等函数、导数及其应用
函数与方程
1.函数的零点
(1)函数零点的定义
函数的零点是什么?零点是点吗?
提示:对于函数y=f(x)(x∈R),我们把使f(x)=0的实数x,叫做函数的零点,函数的零点不是点,是方程f(x)=0的根,是函数y=f(x)的图象与x轴的交点的横坐标,它是一个实数
(2)几个等价关系
方程f(x)=0有实数根 函数y=f(x)的图象与______有
交
点 函数y=f(x)有______.
(3)函数零点的判定(零点存在性定理)
如果函数y=f(x)在区间[a,b]上的图象是连续不
断的一
条
曲线,并且有____________,那么函数y=f(x)在区间________内有零点,即存在c∈(a,b),使得________,这个c
也
就
是f(x)=0的根.
x轴
零点
f(a)·f(b)<0
(a,b)
f(c)=0
温馨提醒:(1)函数f(x)的零点是一个实数,是
方
程f(x)=0
的根,也是函数y=f(x)的图象与x轴交点的横坐标.
(2)函数零点存在性定理是零点存在的一个充分条件,而
不是必要条件;判断零点个数还要根据函数的单调性、对称
性
或结合函数图象.
2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系
Δ>0
Δ=0
Δ<0
二次函数
y=ax2+bx+c
(a>0)的图象
与x轴的交点
_______,_______
(x1,0)或
(x2,0)
无交点
零点个数
2
1
0
(x1,0)
(x2,0)
3.二分法的定义
对于在区间[a,b]上连续不断且________________的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近______,进而得到零点近似值的方法叫
做
二分法.
温馨提醒:二分法是求方程的根的近似值的一种计算方法.其实质是通过不断地“取中点”来逐步缩小零点所在的范围,当达到一定的精确度要求时,所得区间的任一点就是这个函数零点的近似值.
f(a)·f(b)<0
零点
1.如图所示的函数图象与x轴均有交点,其中不能用二分法求图中交点横坐标的是( )
A.①②
B.①③
C.①④
D.③④
B
2.(2012·高考湖北卷改编)函数f(x)=xcos
x在
区间[0,2π]
上的零点的个数为( )
A.2
B.3
C.4
D.5
3.函数f(x)=2x+3x的零点所在的一个区间是( )
A.(-2,-1)
B.(-1,0)
C.(0,1)
D.(1,2)
4.函数y=|x|-cos
x在(-∞,+∞)内有________个零点.
5.已知函数f(x)=x2+x+a(a<0)在区间(0,1)上有零点,则a的取值范围为____________.
B
B
两
(-2,0)
函数零点所在区间的确定
[课堂笔记]
A
判断函数在某个区间上是否存在零点,要根据具体题目灵活处理.当能直接求出零点时,就直接求出进行判断;当不能直接求出时,可根据零点存在性定理判断;当用零点存在性定理也无法判断时可画出图象判断.
C
确定函数零点个数
D
(2)(2014·河北石家庄市模拟考试)[x]表示不超过x的最大整数,例如[2.9]=2,[-4.1]=-5,已知f(x)=x-[x](x∈R),g(x)=log4(x-1),则函数h(x)=f(x)-g(x)的零点个数是( )
A.1
B.2
C.3
D.4
[课堂笔记]
B
判断函数零点个数的方法:
(1)解方程法:令f(x)=0,如果能求出解,则有几个解就有
几个零点;
(2)零点存在性定理法:利用定理不仅要求函数在区
间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合
函数
的
图象与性质(如单调性、奇偶性、周期性、对称性)才能
确
定
函数有多少个零点或零点值所具有的性质;
(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的横
坐
标有几个不同的值,就有几个不同的零点.
C
A
函数零点的综合问题
[课堂笔记]
(0,1)
转化与化归思想在研究函数零点中的应用
B
已知a,b,c∈R,a+b+c=0,a+bc-1=0,则a的取值范
围是_____________________________________.
