沪教版(上海)高中数学高一下册 4.6 对数函数 课件13(共49张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 4.6 对数函数 课件13(共49张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览










文档简介
(共49张PPT)
对数与对数函数
[主干知识梳理]
一、对数的概念
1.对数的定义:
如果
,那么数x叫做以a为底N的对数,记作
,其中
叫做对数的底数,
叫做真数.当a=10时叫常用对数.记作x=
,当a=e时叫自然对数,记作x=
.
ax=N(a>0且a≠1)
x=logaN
a
N
lg
N
ln
N
二、对数函数的概念
1.把y=logax(a>0,a≠1)叫做对数函数,其中x是自变量,函数的定义域是
.
2.函数y=logax(a>0,a≠1)是指数函数y=ax的反函数,函数y=ax与y=logax(a>0,a≠1)的图象关于
对称.
(0,+∞)
y=x
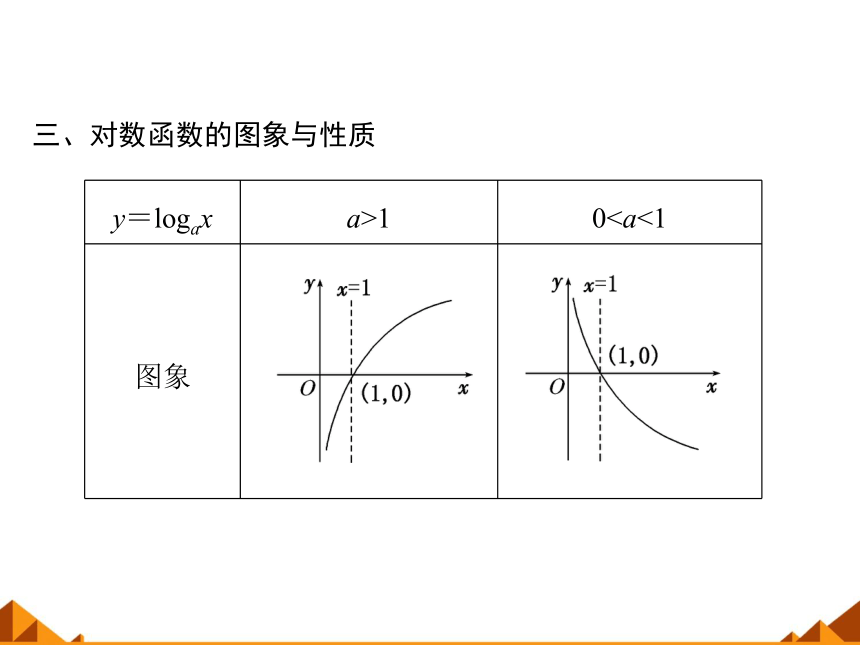
三、对数函数的图象与性质
y=logax
a>1
0图象
性质
定义域:
值域:
过点
,即x=
时,y=
当x>1时,
当0当x>1时,
当0在(0,+∞)上是
在(0,+∞)上是
(0,+∞)
R
(1,0)
1
0
y>0
y<0
y<0
y>0
增函数
减函数
3.函数y=lg
|x|
( )
A.是偶函数,在区间(-∞,0)上单调递增
B.是偶函数,在区间(-∞,0)上单调递减
C.是奇函数,在区间(0,+∞)上单调递减
D.是奇函数,在区间(0,+∞)上单调递增
B [y=lg|x|是偶函数,由图象知在(-∞,0)上单调递减,在(0,+∞)上单调递增.]
[关键要点点拨]
1.在运用性质logaMn=nlogaM时,要特别注意条件,在无M>0的条件下应为logaMn=nloga|M|(n∈N
,且n为偶数).
2.对数值取正、负值的规律:
当a>1且b>1,或00;
当a>1且01时,logab<0.
3.对数函数的定义域及单调性:
在对数式中,真数必须大于0,所以对数函数y=logax的定义域应为{x|x>0}.对数函数的单调性和a的值有关,因而,在研究对数函数的单调性时,要按01进行分类讨论.
对数式的化简与求值
[规律方法]
对数式的化简与求值的常用思路
(1)先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后运用对数运算法则化简合并.
(2)先将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算法则,转化为同底对数真数的积、商、幂再运算.
对数函数的图象及应用
[互动探究]
若本例(2)变为:若不等式(x-1)2解析 设f1(x)=(x-1)2,f2(x)=logax,
要使当x∈(1,2)时,不等式(x-1)2只需f1(x)=(x-1)2在(1,2)上的图象在f2(x)=logax图象的下方即可.
当0当a>1时,如图,
要使x∈(1,2)时f1(x)=(x-1)2的图象在f2(x)=logax的图象下方,
只需f1(2)≤f2(2),
即(2-1)2≤loga2,
又即loga2≥1.
所以1即实数a的取值范围是(1,2].
答案 (1,2]
[规律方法]
1.对一些可通过平移、对称变换能作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合求解.
2.一些对数型方程、不等式问题的求解,常转化为相应函数图象问题,利用数形结合法求解.
[典题导入]
已知函数f(x)=log4(ax2+2x+3).
(1)若f(x)定义域为R,求a的取值范围;
(2)若f(1)=1,求f(x)的单调区间;
(3)是否存在实数a,使f(x)的最小值为0?若存在,求出a的值;若不存在,说明理由.
对数函数的性质及应用
[规律方法]
研究复合函数y=loga
f(x)的单调性(最值)时,应先研究其定义域,分析复合的特点,结合函数u=f(x)及y=logau的单调性(最值)情况确定函数y=logaf(x)的单调性(最值)(其中a>0,且a≠1).
[跟踪训练]
3.已知f(x)=loga(ax-1)(a>0且a≠1).
(1)求f(x)的定义域;
(2)判断函数f(x)的单调性.
解析 (1)由ax-1>0得ax>1,当a>1时,x>0;
当0∴当a>1时,f(x)的定义域为(0,+∞);
当0已知x=ln
π,y=log52,z=e
,则
( )
A.x<y<z
B.z<x<y
C.z<y<x
D.y<z<x
【创新探究】 巧用中间量比较大小
【高手支招】 本题在比较三个数的大小时利用中间值,进行第一次比较时,中间值常选用的有0,1,由指数、对数式可知x>1,00;反之,logaN<0.
2.(2013·福建高考)函数f(x)=ln(x2+1)的图象大致是
( )
A [由f(0)=0可知函数图象经过原点.
又f(-x)=f(x),所以函数图象关于y轴对称.
故选A.]
对数与对数函数
[主干知识梳理]
一、对数的概念
1.对数的定义:
如果
,那么数x叫做以a为底N的对数,记作
,其中
叫做对数的底数,
叫做真数.当a=10时叫常用对数.记作x=
,当a=e时叫自然对数,记作x=
.
ax=N(a>0且a≠1)
x=logaN
a
N
lg
N
ln
N
二、对数函数的概念
1.把y=logax(a>0,a≠1)叫做对数函数,其中x是自变量,函数的定义域是
.
2.函数y=logax(a>0,a≠1)是指数函数y=ax的反函数,函数y=ax与y=logax(a>0,a≠1)的图象关于
对称.
(0,+∞)
y=x
三、对数函数的图象与性质
y=logax
a>1
0
性质
定义域:
值域:
过点
,即x=
时,y=
当x>1时,
当0
当0
在(0,+∞)上是
(0,+∞)
R
(1,0)
1
0
y>0
y<0
y<0
y>0
增函数
减函数
3.函数y=lg
|x|
( )
A.是偶函数,在区间(-∞,0)上单调递增
B.是偶函数,在区间(-∞,0)上单调递减
C.是奇函数,在区间(0,+∞)上单调递减
D.是奇函数,在区间(0,+∞)上单调递增
B [y=lg|x|是偶函数,由图象知在(-∞,0)上单调递减,在(0,+∞)上单调递增.]
[关键要点点拨]
1.在运用性质logaMn=nlogaM时,要特别注意条件,在无M>0的条件下应为logaMn=nloga|M|(n∈N
,且n为偶数).
2.对数值取正、负值的规律:
当a>1且b>1,或0
当a>1且0
3.对数函数的定义域及单调性:
在对数式中,真数必须大于0,所以对数函数y=logax的定义域应为{x|x>0}.对数函数的单调性和a的值有关,因而,在研究对数函数的单调性时,要按0
对数式的化简与求值
[规律方法]
对数式的化简与求值的常用思路
(1)先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后运用对数运算法则化简合并.
(2)先将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算法则,转化为同底对数真数的积、商、幂再运算.
对数函数的图象及应用
[互动探究]
若本例(2)变为:若不等式(x-1)2
要使当x∈(1,2)时,不等式(x-1)2
当0
要使x∈(1,2)时f1(x)=(x-1)2的图象在f2(x)=logax的图象下方,
只需f1(2)≤f2(2),
即(2-1)2≤loga2,
又即loga2≥1.
所以1
答案 (1,2]
[规律方法]
1.对一些可通过平移、对称变换能作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合求解.
2.一些对数型方程、不等式问题的求解,常转化为相应函数图象问题,利用数形结合法求解.
[典题导入]
已知函数f(x)=log4(ax2+2x+3).
(1)若f(x)定义域为R,求a的取值范围;
(2)若f(1)=1,求f(x)的单调区间;
(3)是否存在实数a,使f(x)的最小值为0?若存在,求出a的值;若不存在,说明理由.
对数函数的性质及应用
[规律方法]
研究复合函数y=loga
f(x)的单调性(最值)时,应先研究其定义域,分析复合的特点,结合函数u=f(x)及y=logau的单调性(最值)情况确定函数y=logaf(x)的单调性(最值)(其中a>0,且a≠1).
[跟踪训练]
3.已知f(x)=loga(ax-1)(a>0且a≠1).
(1)求f(x)的定义域;
(2)判断函数f(x)的单调性.
解析 (1)由ax-1>0得ax>1,当a>1时,x>0;
当0
当0
π,y=log52,z=e
,则
( )
A.x<y<z
B.z<x<y
C.z<y<x
D.y<z<x
【创新探究】 巧用中间量比较大小
【高手支招】 本题在比较三个数的大小时利用中间值,进行第一次比较时,中间值常选用的有0,1,由指数、对数式可知x>1,0
2.(2013·福建高考)函数f(x)=ln(x2+1)的图象大致是
( )
A [由f(0)=0可知函数图象经过原点.
又f(-x)=f(x),所以函数图象关于y轴对称.
故选A.]
