2020—2021学年人教版数学九年级下册—特殊角的三角涵数应用及用计算器求角的三角涵数值 课件28.1 锐角三角函数(共32张PPT)
文档属性
| 名称 | 2020—2021学年人教版数学九年级下册—特殊角的三角涵数应用及用计算器求角的三角涵数值 课件28.1 锐角三角函数(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-02 07:46:04 | ||
图片预览





文档简介
(共32张PPT)
特殊角的三角函数值及用计算器求角的三角涵数值
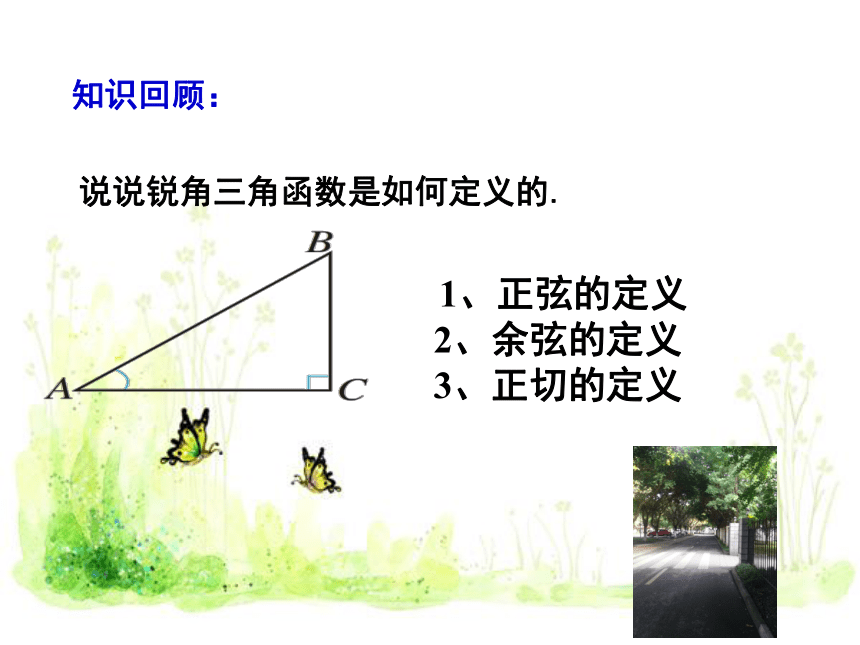
知识回顾:
说说锐角三角函数是如何定义的.
1、正弦的定义
2、余弦的定义
3、正切的定义
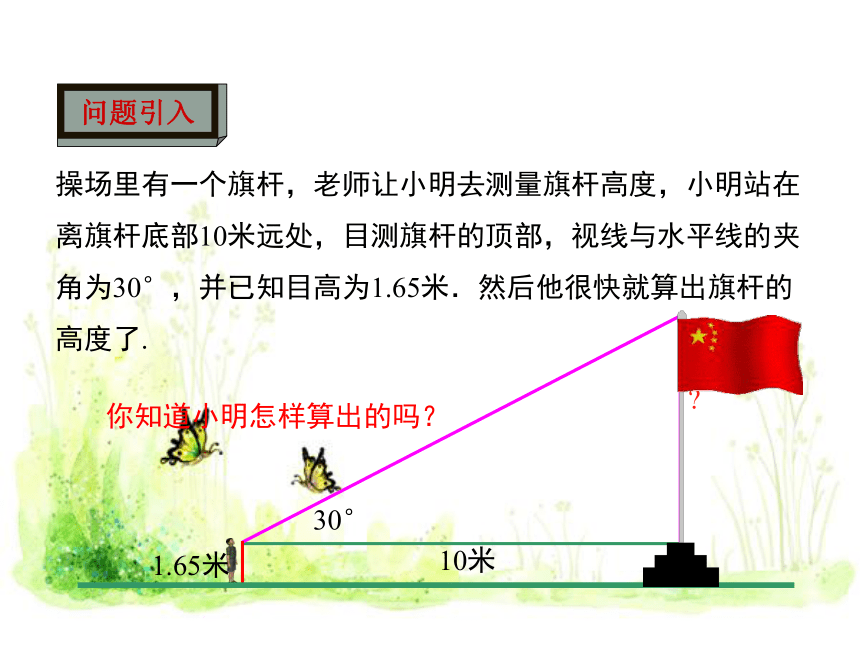
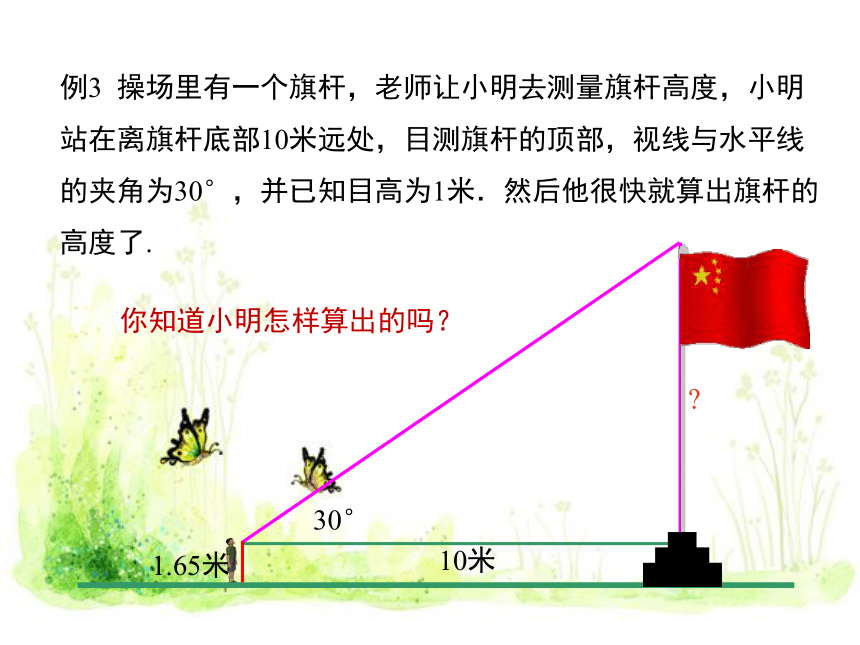
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30°,并已知目高为1.65米.然后他很快就算出旗杆的高度了.
1.65米
10米
30°
你知道小明怎样算出的吗?
问题引入
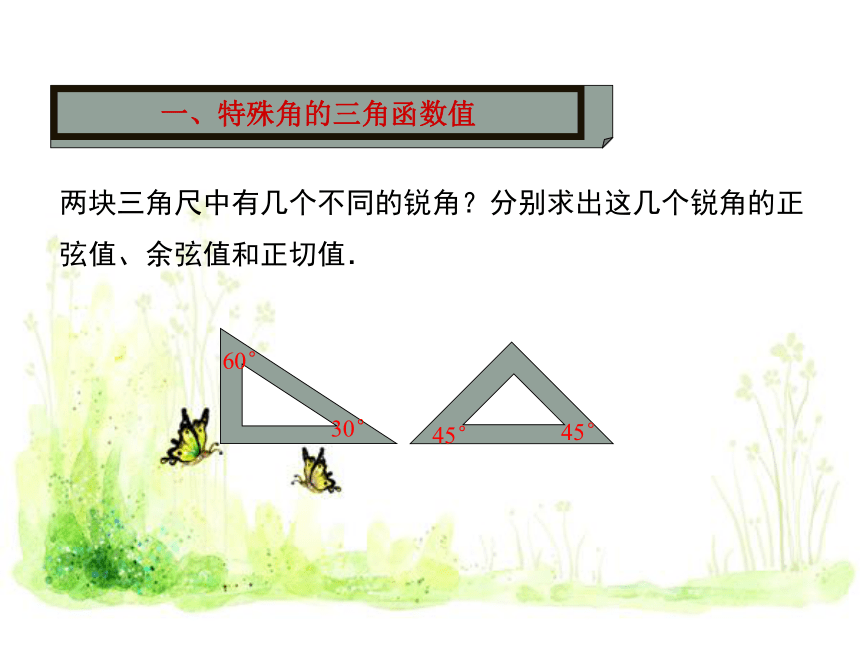
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
一、特殊角的三角函数值
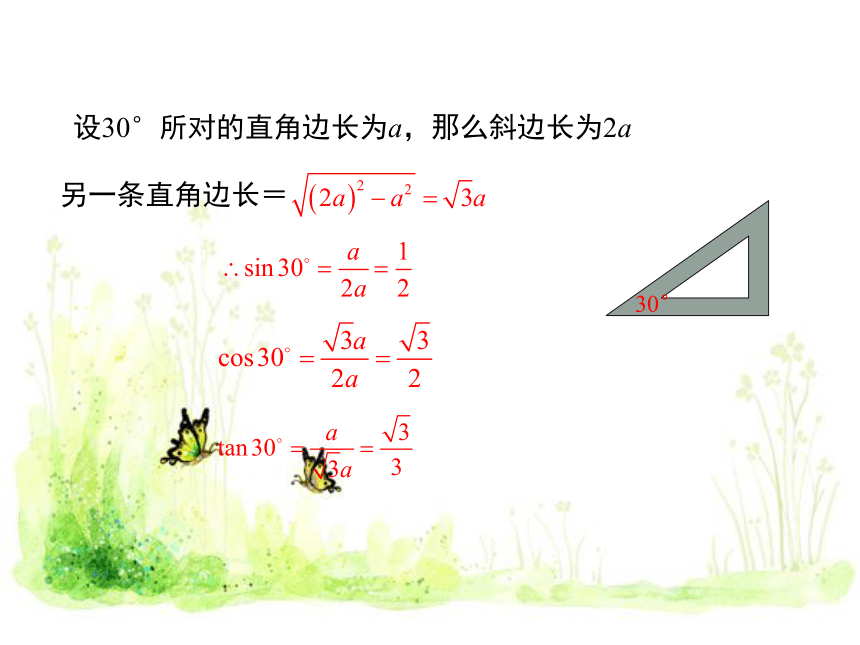
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
设两条直角边长为a,则斜边长=
60°
45°
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin
a
cos
a
tan
a
归纳总结
例1
求下列各式的值:
(1)cos260°+sin260°;(2)
解
:
(1)原式=
(2)原式=
状熟记:特殊角的三角涵数值路
2、求下列各式的值:
(1)1-2
sin30°cos30°;
(2)3tan30°-tan45°+2sin60°;
.
解:
(1)1-2
sin30°cos30°
(2)3tan30°-tan45°+2sin60°
例3
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30°,并已知目高为1米.然后他很快就算出旗杆的高度了.
1.65米
10米
30°
你知道小明怎样算出的吗?
1.65米
10米
30°
A
B
C
D
E
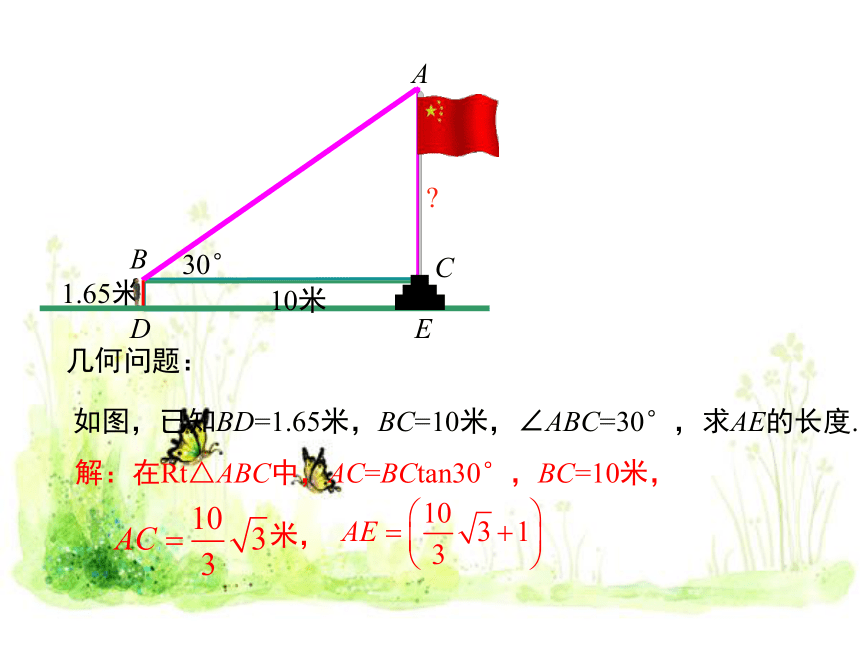
如图,已知BD=1.65米,BC=10米,∠ABC=30°,求AE的长度.
几何问题:
解:在Rt△ABC中,AC=BCtan30°,BC=10米,
米,
例2
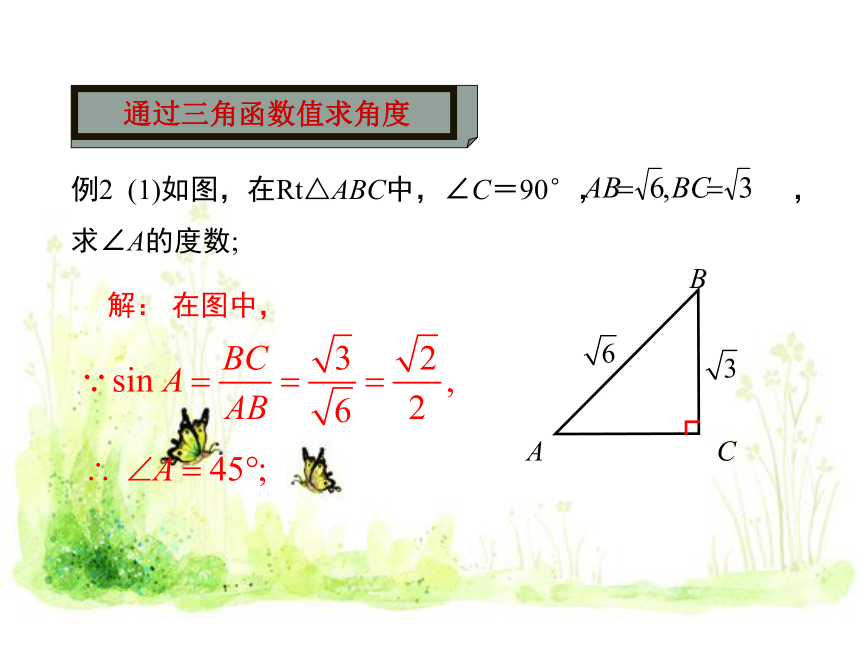
(1)如图,在Rt△ABC中,∠C=90°,
,求∠A的度数;
解:
在图中,
A
B
C
通过三角函数值求角度
解:
在图中,
A
B
O
(2)如图,AO是圆锥的高,OB是底面半径,AO=
OB,
求
的度数.
2.在△ABC中,若
,则∠C=( )
A.30°
B.60°
C.90°
D.120°
1.
tan(α+20°)=1,锐角α的度数应是( )
A.40°
B.30°
C.20°
D.10°
D
D
当堂练习
问题1
求
sin18°的值.
第一步:按计算器
键,
sin
第二步:输入角度值18,
屏幕显示结果sin18°=0.309
016
994
借助计算器求锐角三角函数值
不同计算器操作的步骤可能有所不同
二、用计算器求锐角的三角函数值或角的度数
问题2
求
tan30°36'的值.
tan
第一步:按计算器
键,
第二步:输入角度值30.6
(因为30°36'=30.6°)
屏幕显示答案:0.591
398
351
问题3
已知sinA=0.501
8,求∠A的度数.
第一步:按计算器
键,
2nd
F
sin-1
第二步:然后输入函数值0.
501
8
屏幕显示答案:
30.119
158
67°
(按实际需要进行精确)
(1)
≈
0.6428
0.2672
31.5
(3)
若
α
=0.5225,则α≈
(精确到0.1°);
(4)
若
=0.8090,则α≈
(精确到0.1°).
1.利用计算器计算:
(2)
≈
sin
sin
α
(精确到0.0001
);
(精确到0.0001
);
54.0
当堂练习
用计算器求下列锐角三角函数值;
(1)
sin20°=
,
cos70°=
;
sin35°=
,cos55°=
;
sin15°32
'
=
,cos74°28
'
=
.
0.3420
0.3420
0.5735
0.5735
0.2678
0.2678
你能得出什么结论?
二、利用计算器探索三角函数的性质
(2)
sin20°=
cos20°=
,
sin220°=
,
cos220°=
;
sin35°=
,cos35°=
,
sin235°=
,cos235°=
;
0.3420
0.5735
0.9397
0.1170
0.8830
0.8192
0.3290
0.6710
你能得出什么结论?
(3)
tan20°=
,
tan70°=
,
tan20°×tan70°=
;
tan35°=
,tan55°=
,tan35°×tan55°=
0.3640
2.7470
1
0.7000
1.4281
1
拓广探索
用计算器求下列锐角三角函数值,并填入表中:
正弦值随着角度的增大(或减小)而增大(或减小);
余弦值随着角度的增大(或减小)而减小(或增大);
正切值随着角度的增大(或减小)而增大(或减小).
归
纳
1.
2cos(α-10°)=1,则锐角α=
.
A.
B.
C.
D.
70°
随堂演练
2.
已知α为锐角,tanα=
,则cosα等于(
)
A
3.在Rt△ABC中,∠C=90°,则下列式子定成立的是( )
A.sinA=sinB
B.cosA=cosB
C.tanA=tanB
D.sinA=cosB
D
4.已知:sin232°+cos2α=1,则锐角α等于( B)
A.32°
B.58°
C.68°
D.以上结论都不对
A
5.下列各式中一定成立的是(
)
A.tan75°>tan48°>tan15°
B.
tan75°<tan48°<tan15°
C.
cos75°>cos48°>cos15°
D.
sin75°<sin48°<sin15°
6.计算:tan33°·tan34°·tan35°·tan55°·tan56°·tan57°.
解:tan33°·tan34°·tan35°·tan55°·tan56°·tan57°
=(tan33°·
tan57°)
(tan34°·
tan56°)
(tan35°·
tan55°)
=1.
综合应用
7、在△ABC中,锐角A,B满足
=0,则△ABC是(
)
A.等腰三角形
B.等边三角形
C.等腰直角三角形
D.直角三角形
D
8、如图,△ABC内接于⊙O,AB,CD为⊙O的直径,DE⊥AB于点E,BC=1,AC=
,则∠D的度数为
.
30
课堂小结
30°
45°
60°
sin
A
cos
A
tan
A
锐角A
锐角
三角函数
用计算器求锐角三角函数值及锐角
用计算器求锐角的三角函数值或角的度数
不同的计算器操作步骤可能有所不同
利用计算器探索锐三角函数的新知
正弦值随着角度的增大(或减小)而增大(或减小);
余弦值随着角度的增大(或减小)而减小(或增大);
正切值随着角度的增大(或减小)而增大(或减小).
课堂小结
作业
P68-70
习题28.1
3、4、5、8
练习册
再见
特殊角的三角函数值及用计算器求角的三角涵数值
知识回顾:
说说锐角三角函数是如何定义的.
1、正弦的定义
2、余弦的定义
3、正切的定义
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30°,并已知目高为1.65米.然后他很快就算出旗杆的高度了.
1.65米
10米
30°
你知道小明怎样算出的吗?
问题引入
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
一、特殊角的三角函数值
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
设两条直角边长为a,则斜边长=
60°
45°
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin
a
cos
a
tan
a
归纳总结
例1
求下列各式的值:
(1)cos260°+sin260°;(2)
解
:
(1)原式=
(2)原式=
状熟记:特殊角的三角涵数值路
2、求下列各式的值:
(1)1-2
sin30°cos30°;
(2)3tan30°-tan45°+2sin60°;
.
解:
(1)1-2
sin30°cos30°
(2)3tan30°-tan45°+2sin60°
例3
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30°,并已知目高为1米.然后他很快就算出旗杆的高度了.
1.65米
10米
30°
你知道小明怎样算出的吗?
1.65米
10米
30°
A
B
C
D
E
如图,已知BD=1.65米,BC=10米,∠ABC=30°,求AE的长度.
几何问题:
解:在Rt△ABC中,AC=BCtan30°,BC=10米,
米,
例2
(1)如图,在Rt△ABC中,∠C=90°,
,求∠A的度数;
解:
在图中,
A
B
C
通过三角函数值求角度
解:
在图中,
A
B
O
(2)如图,AO是圆锥的高,OB是底面半径,AO=
OB,
求
的度数.
2.在△ABC中,若
,则∠C=( )
A.30°
B.60°
C.90°
D.120°
1.
tan(α+20°)=1,锐角α的度数应是( )
A.40°
B.30°
C.20°
D.10°
D
D
当堂练习
问题1
求
sin18°的值.
第一步:按计算器
键,
sin
第二步:输入角度值18,
屏幕显示结果sin18°=0.309
016
994
借助计算器求锐角三角函数值
不同计算器操作的步骤可能有所不同
二、用计算器求锐角的三角函数值或角的度数
问题2
求
tan30°36'的值.
tan
第一步:按计算器
键,
第二步:输入角度值30.6
(因为30°36'=30.6°)
屏幕显示答案:0.591
398
351
问题3
已知sinA=0.501
8,求∠A的度数.
第一步:按计算器
键,
2nd
F
sin-1
第二步:然后输入函数值0.
501
8
屏幕显示答案:
30.119
158
67°
(按实际需要进行精确)
(1)
≈
0.6428
0.2672
31.5
(3)
若
α
=0.5225,则α≈
(精确到0.1°);
(4)
若
=0.8090,则α≈
(精确到0.1°).
1.利用计算器计算:
(2)
≈
sin
sin
α
(精确到0.0001
);
(精确到0.0001
);
54.0
当堂练习
用计算器求下列锐角三角函数值;
(1)
sin20°=
,
cos70°=
;
sin35°=
,cos55°=
;
sin15°32
'
=
,cos74°28
'
=
.
0.3420
0.3420
0.5735
0.5735
0.2678
0.2678
你能得出什么结论?
二、利用计算器探索三角函数的性质
(2)
sin20°=
cos20°=
,
sin220°=
,
cos220°=
;
sin35°=
,cos35°=
,
sin235°=
,cos235°=
;
0.3420
0.5735
0.9397
0.1170
0.8830
0.8192
0.3290
0.6710
你能得出什么结论?
(3)
tan20°=
,
tan70°=
,
tan20°×tan70°=
;
tan35°=
,tan55°=
,tan35°×tan55°=
0.3640
2.7470
1
0.7000
1.4281
1
拓广探索
用计算器求下列锐角三角函数值,并填入表中:
正弦值随着角度的增大(或减小)而增大(或减小);
余弦值随着角度的增大(或减小)而减小(或增大);
正切值随着角度的增大(或减小)而增大(或减小).
归
纳
1.
2cos(α-10°)=1,则锐角α=
.
A.
B.
C.
D.
70°
随堂演练
2.
已知α为锐角,tanα=
,则cosα等于(
)
A
3.在Rt△ABC中,∠C=90°,则下列式子定成立的是( )
A.sinA=sinB
B.cosA=cosB
C.tanA=tanB
D.sinA=cosB
D
4.已知:sin232°+cos2α=1,则锐角α等于( B)
A.32°
B.58°
C.68°
D.以上结论都不对
A
5.下列各式中一定成立的是(
)
A.tan75°>tan48°>tan15°
B.
tan75°<tan48°<tan15°
C.
cos75°>cos48°>cos15°
D.
sin75°<sin48°<sin15°
6.计算:tan33°·tan34°·tan35°·tan55°·tan56°·tan57°.
解:tan33°·tan34°·tan35°·tan55°·tan56°·tan57°
=(tan33°·
tan57°)
(tan34°·
tan56°)
(tan35°·
tan55°)
=1.
综合应用
7、在△ABC中,锐角A,B满足
=0,则△ABC是(
)
A.等腰三角形
B.等边三角形
C.等腰直角三角形
D.直角三角形
D
8、如图,△ABC内接于⊙O,AB,CD为⊙O的直径,DE⊥AB于点E,BC=1,AC=
,则∠D的度数为
.
30
课堂小结
30°
45°
60°
sin
A
cos
A
tan
A
锐角A
锐角
三角函数
用计算器求锐角三角函数值及锐角
用计算器求锐角的三角函数值或角的度数
不同的计算器操作步骤可能有所不同
利用计算器探索锐三角函数的新知
正弦值随着角度的增大(或减小)而增大(或减小);
余弦值随着角度的增大(或减小)而减小(或增大);
正切值随着角度的增大(或减小)而增大(或减小).
课堂小结
作业
P68-70
习题28.1
3、4、5、8
练习册
再见
