西师版六年级上册数学表格式教案3.3一个数除以分数
文档属性
| 名称 | 西师版六年级上册数学表格式教案3.3一个数除以分数 |
|
|
| 格式 | docx | ||
| 文件大小 | 64.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 00:00:00 | ||
图片预览


文档简介
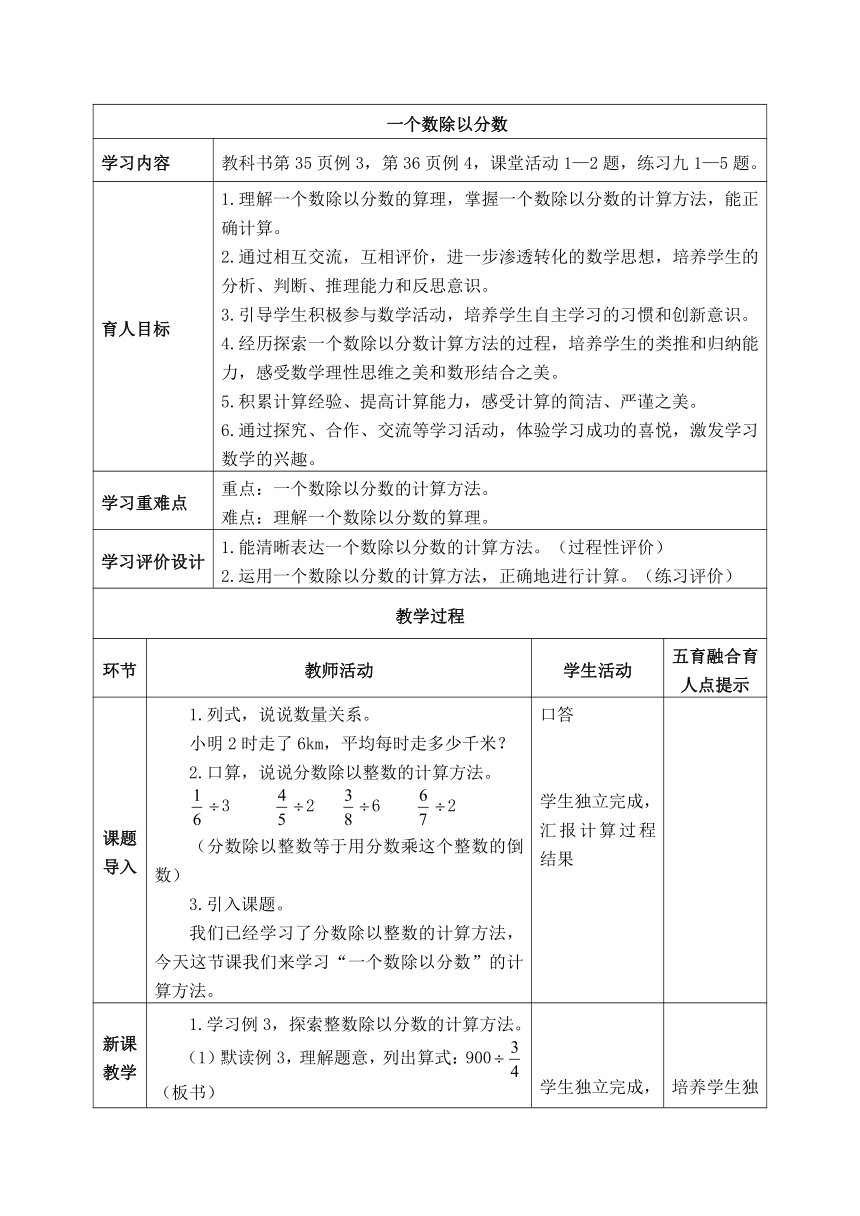
一个数除以分数
学习内容
教科书第35页例3,第36页例4,课堂活动1—2题,练习九1—5题。
育人目标
1.理解一个数除以分数的算理,掌握一个数除以分数的计算方法,能正确计算。
2.通过相互交流,互相评价,进一步渗透转化的数学思想,培养学生的分析、判断、推理能力和反思意识。
3.引导学生积极参与数学活动,培养学生自主学习的习惯和创新意识。
4.经历探索一个数除以分数计算方法的过程,培养学生的类推和归纳能力,感受数学理性思维之美和数形结合之美。
5.积累计算经验、提高计算能力,感受计算的简洁、严谨之美。
6.通过探究、合作、交流等学习活动,体验学习成功的喜悦,激发学习数学的兴趣。
学习重难点
重点:一个数除以分数的计算方法。
难点:理解一个数除以分数的算理。
学习评价设计
1.能清晰表达一个数除以分数的计算方法。(过程性评价)
2.运用一个数除以分数的计算方法,正确地进行计算。(练习评价)
教学过程
环节
教师活动
学生活动
五育融合育人点提示
课题导入
1.列式,说说数量关系。
小明2时走了6km,平均每时走多少千米?
2.口算,说说分数除以整数的计算方法。
3
2
6
2
(分数除以整数等于用分数乘这个整数的倒数)
3.引入课题。
我们已经学习了分数除以整数的计算方法,今天这节课我们来学习“一个数除以分数”的计算方法。
口答
学生独立完成,汇报计算过程结果
新课教学
1.学习例3,探索整数除以分数的计算方法。
(1)默读例3,理解题意,列出算式:900(板书)
当分数除以整数时,我们可以把它转化成乘整数的倒数。(板书:转化)现在是一个数除以分数,又怎样算哪?
(2)900÷应怎样计算?你能转化为我们已学的知识解决吗?试试看(可以用算式或线段图表示出自己的思考过程)
(3)小组交流,你是怎样想的又怎样算的?
(4)全班汇报,预设学生可能会出现以下几种情况:
①把化成0.75,900÷=900÷0.75=1200(m)。
②利用商不变的性质,被除数和除数同时扩大到原来的4倍。
900÷=(900×4)÷(×4)
=900×4÷3
=1200(m)
③利用线段图理解:
先画一条线段表示1分行的路程,怎么样表示分行了900m这个条件?
(1分=分,将线段平均分成4份,其中的3份就是分行的路程)
根据学生回答把线段图补充完整
要求1分行了多少米?可以先算什么,再算什么?,根据回答板书:
900÷
=900÷3×4
=900××4
=900×
=1200(米)
④观察思考:这个算式前后有什么变化
(5)比较三种算法,你喜欢哪一种?为什么?
(6)想一想:整数除以分数怎样算?
小结:整数除以分数等于用整数乘这个分数的倒数。
(7)试一试。
8
21
6
引导:如果被除数变成分数,又该怎样计算?
2.学习例4,探索分数除以分数的计算方法。
(1)出示例4,计算
(2)学生尝试计算。
=×=
(3)学生用自己的方法来验证结果是否正确。
3.总结计算法则。
(1)分数除以分数怎样算?
(2)总结算法:无论是整数除以分数,还是分数除以分数,都可以转化成乘法来计算,也就是说一个数除以分数,等于这个数乘分数的倒数。(板书)
学生独立完成,再汇报交流
学生独立思考,尝试计算
小组交流算法
全班交流算法,集体评价
对比算法,说出喜欢原因
独立思考汇报
独立尝试
独立尝试计算
验证计算结果
讨论交流,小结算法。
培养学生独立探究的精神。
在探索一个数除以分数计算方法的过程中感受数学理性思维之美和数形结合之美。
通过探究、合作、交流等学习活动,体验学习成功的喜悦,激发学习数学的兴趣。
培养学生的类推和归纳能力。
课堂练习
1.课堂活动第1题
独立计算,说一说当除数大于1或小于1时,商与被除数有什么关系?
在学生乘法发表意见的基础上归纳出:
被除数不为0时,如果除数>1,那么商<被除数;如果除数=1,那么商=被除数;
如果除数<1,那么商>被除数。
2.课堂活动第2题,根据规律直接判断。
练习九1-5题。
3.学生独立完成,发现问题,及时解决。
独立计算,同桌交流,集体评价
独立思考判断汇报评价。
积累计算经验、提高计算能力,感受计算的简洁、严谨之美。
课堂小结
这节课你有什么收获 是通过什么方法获得的?你认为计算一个数除以分数要注意什么问题?
学生回顾,交流
板书
设计
一个数除以分数
900÷
一个数除以分数等于用这个数乘这个分数的倒数。
教学
反思
学习内容
教科书第35页例3,第36页例4,课堂活动1—2题,练习九1—5题。
育人目标
1.理解一个数除以分数的算理,掌握一个数除以分数的计算方法,能正确计算。
2.通过相互交流,互相评价,进一步渗透转化的数学思想,培养学生的分析、判断、推理能力和反思意识。
3.引导学生积极参与数学活动,培养学生自主学习的习惯和创新意识。
4.经历探索一个数除以分数计算方法的过程,培养学生的类推和归纳能力,感受数学理性思维之美和数形结合之美。
5.积累计算经验、提高计算能力,感受计算的简洁、严谨之美。
6.通过探究、合作、交流等学习活动,体验学习成功的喜悦,激发学习数学的兴趣。
学习重难点
重点:一个数除以分数的计算方法。
难点:理解一个数除以分数的算理。
学习评价设计
1.能清晰表达一个数除以分数的计算方法。(过程性评价)
2.运用一个数除以分数的计算方法,正确地进行计算。(练习评价)
教学过程
环节
教师活动
学生活动
五育融合育人点提示
课题导入
1.列式,说说数量关系。
小明2时走了6km,平均每时走多少千米?
2.口算,说说分数除以整数的计算方法。
3
2
6
2
(分数除以整数等于用分数乘这个整数的倒数)
3.引入课题。
我们已经学习了分数除以整数的计算方法,今天这节课我们来学习“一个数除以分数”的计算方法。
口答
学生独立完成,汇报计算过程结果
新课教学
1.学习例3,探索整数除以分数的计算方法。
(1)默读例3,理解题意,列出算式:900(板书)
当分数除以整数时,我们可以把它转化成乘整数的倒数。(板书:转化)现在是一个数除以分数,又怎样算哪?
(2)900÷应怎样计算?你能转化为我们已学的知识解决吗?试试看(可以用算式或线段图表示出自己的思考过程)
(3)小组交流,你是怎样想的又怎样算的?
(4)全班汇报,预设学生可能会出现以下几种情况:
①把化成0.75,900÷=900÷0.75=1200(m)。
②利用商不变的性质,被除数和除数同时扩大到原来的4倍。
900÷=(900×4)÷(×4)
=900×4÷3
=1200(m)
③利用线段图理解:
先画一条线段表示1分行的路程,怎么样表示分行了900m这个条件?
(1分=分,将线段平均分成4份,其中的3份就是分行的路程)
根据学生回答把线段图补充完整
要求1分行了多少米?可以先算什么,再算什么?,根据回答板书:
900÷
=900÷3×4
=900××4
=900×
=1200(米)
④观察思考:这个算式前后有什么变化
(5)比较三种算法,你喜欢哪一种?为什么?
(6)想一想:整数除以分数怎样算?
小结:整数除以分数等于用整数乘这个分数的倒数。
(7)试一试。
8
21
6
引导:如果被除数变成分数,又该怎样计算?
2.学习例4,探索分数除以分数的计算方法。
(1)出示例4,计算
(2)学生尝试计算。
=×=
(3)学生用自己的方法来验证结果是否正确。
3.总结计算法则。
(1)分数除以分数怎样算?
(2)总结算法:无论是整数除以分数,还是分数除以分数,都可以转化成乘法来计算,也就是说一个数除以分数,等于这个数乘分数的倒数。(板书)
学生独立完成,再汇报交流
学生独立思考,尝试计算
小组交流算法
全班交流算法,集体评价
对比算法,说出喜欢原因
独立思考汇报
独立尝试
独立尝试计算
验证计算结果
讨论交流,小结算法。
培养学生独立探究的精神。
在探索一个数除以分数计算方法的过程中感受数学理性思维之美和数形结合之美。
通过探究、合作、交流等学习活动,体验学习成功的喜悦,激发学习数学的兴趣。
培养学生的类推和归纳能力。
课堂练习
1.课堂活动第1题
独立计算,说一说当除数大于1或小于1时,商与被除数有什么关系?
在学生乘法发表意见的基础上归纳出:
被除数不为0时,如果除数>1,那么商<被除数;如果除数=1,那么商=被除数;
如果除数<1,那么商>被除数。
2.课堂活动第2题,根据规律直接判断。
练习九1-5题。
3.学生独立完成,发现问题,及时解决。
独立计算,同桌交流,集体评价
独立思考判断汇报评价。
积累计算经验、提高计算能力,感受计算的简洁、严谨之美。
课堂小结
这节课你有什么收获 是通过什么方法获得的?你认为计算一个数除以分数要注意什么问题?
学生回顾,交流
板书
设计
一个数除以分数
900÷
一个数除以分数等于用这个数乘这个分数的倒数。
教学
反思
