苏科版数学七年级上册 6.3 余角、补角、对顶角 课件(共18张PPT)
文档属性
| 名称 | 苏科版数学七年级上册 6.3 余角、补角、对顶角 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 747.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-02 08:52:18 | ||
图片预览



文档简介
(共18张PPT)
初中数学七年级上册
(苏科版)
§6.3
余角、补角、对顶角
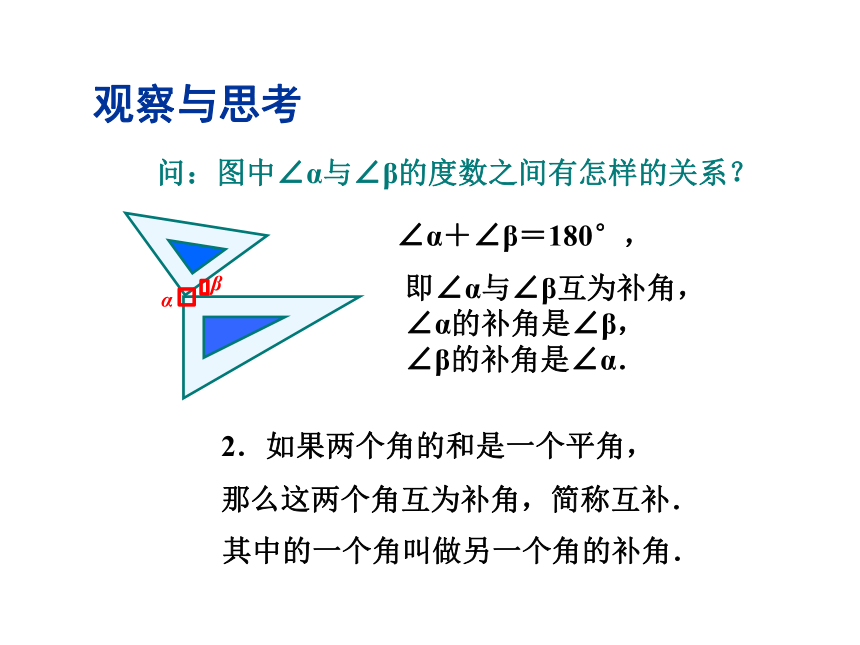
观察与思考
问:图中∠α与∠β的度数之间有怎样的关系?
α
β
1.如果两个角的和是一个直角,
那么这两个角互为余角,简称互余.
其中的一个角叫做另一个角的余角.
即∠α与∠β互为余角,
∠α的余角是∠β,
∠β的余角是∠α.
∠α+∠β=90°,
问:图中∠α与∠β的度数之间有怎样的关系?
观察与思考
α
β
2.如果两个角的和是一个平角,
那么这两个角互为补角,简称互补.
其中的一个角叫做另一个角的补角.
即∠α与∠β互为补角,
∠α的补角是∠β,
∠β的补角是∠α.
∠α+∠β=180°,
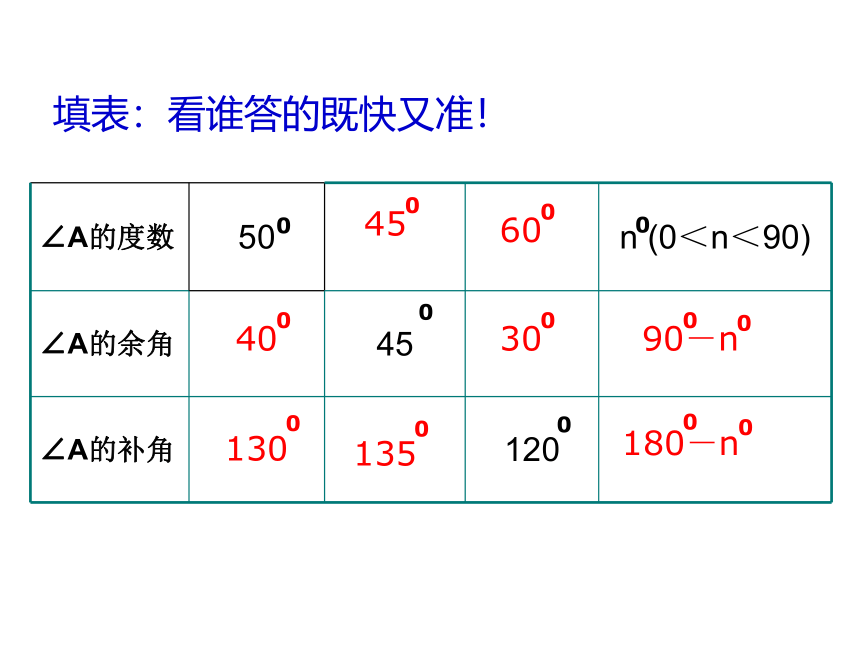
填表:看谁答的既快又准!
∠A的度数
50
n
(0<n<90)
∠A的余角
45
∠A的补角
120
0
0
0
0
40
0
130
0
135
0
45
0
60
0
30
0
90-n
0
0
180-n
0
0
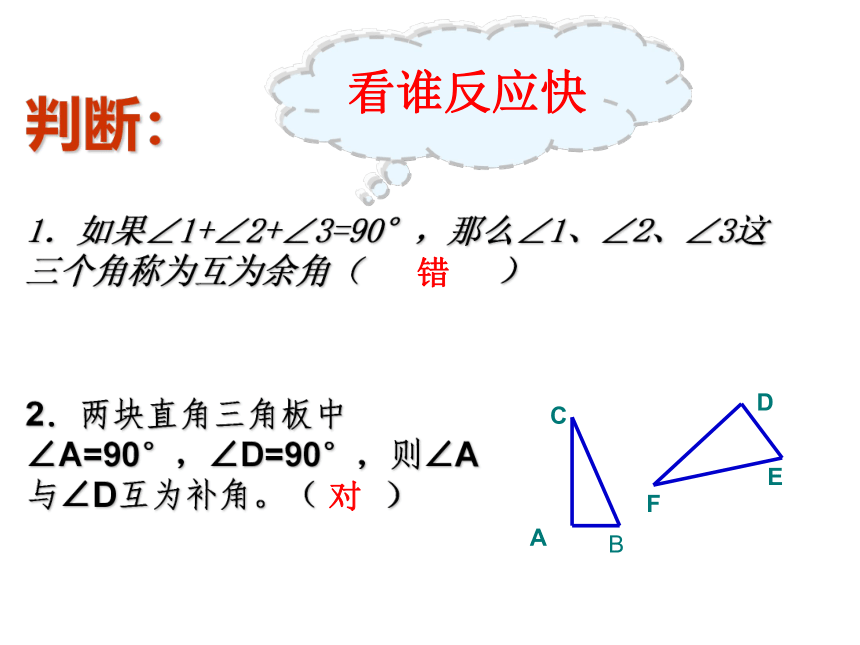
判断:
1.如果∠1+∠2+∠3=90°,那么∠1、∠2、∠3这三个角称为互为余角(
)
2.两块直角三角板中∠A=90°,∠D=90°,则∠A与∠D互为补角。(
)
A
C
D
E
F
B
看谁反应快
错
对
3.一个角的补角一定比这个角大。
(
)
4.互补的两个角中,至少有一个角大于或等于直角(
)
5.两个互余的角都是锐角。(
)
对
错
对
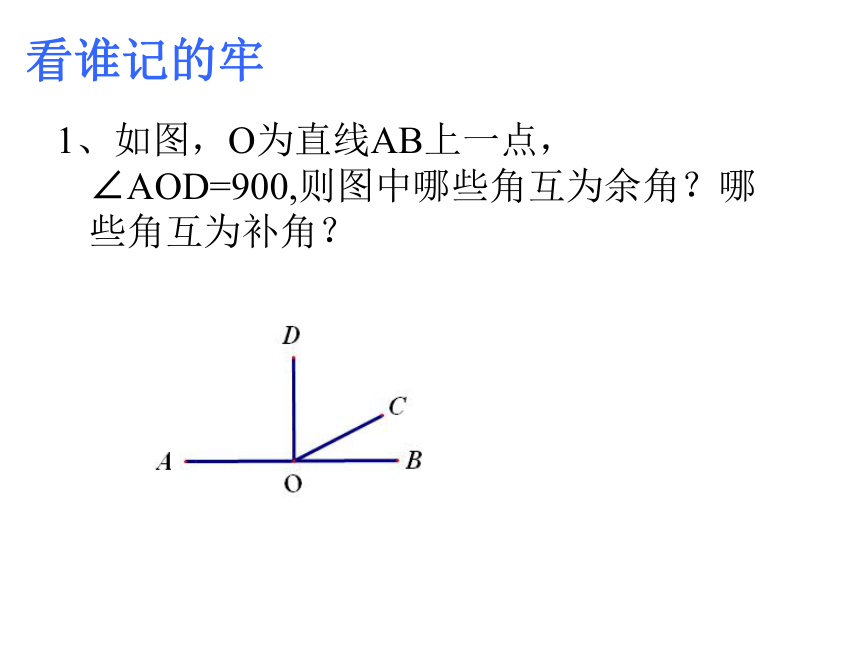
看谁记的牢
1、如图,O为直线AB上一点,∠AOD=900,则图中哪些角互为余角?哪些角互为补角?
知识提升
如图,如果∠1与∠2互余,∠1与∠3互余,那么∠2与∠3相等吗?为什么?
1
2
3
同角的余角相等;
理由:∵∠1与∠
2互余,
∠1与∠3互余,
∴∠
2=
90
°
-
∠1,
∠3=
90
°
-
∠1
∴∠2=∠3
解:
∠2与∠3相等.
知识提升
如图,如果∠1与∠2互补,∠1与∠3互补,那么∠2与∠3的大小关系如何?说明你的理由。
1
2
3
同角的补角相等;
理由:∵∠1与∠
2互补,
∠1与∠3互补,
∴∠
2=
180
°
-
∠1,
∠3=
180
°
-
∠1
∴∠2=∠3
解:
∠2与∠3相等.
如果把互余改为互补,
∠2与∠4仍相等吗
如图,∠1和∠2互余,∠3和∠4互余,若∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
等角的余角相等
理由:∵∠1与∠2互余
∴∠2=90o-∠1
∵∠3与∠4互余
∴∠4=90o-∠3
又∵∠1=∠3
∴∠2=∠4
解:
∠2与∠4相等
等角的补角相等
余角性质:同角(或等角)的余角相等。
几何语言:
∵
∠1+
∠
2=900
∠
1+
∠
3
=
900
几何语言:
∵
∠1+
∠
2=900
∠
3+
∠
4
=
900
又∵
∠
1
=
∠
3
∴
∠
2
=
∠
3
(同角的余角相等)
∴
∠
2
=
∠
4
(等角的余角相等)
同角(或等角)的补角相等。
补角性质:
知识应用
1.如图,∠A+∠B=90,∠BCD+∠B=90,∠A与∠BCD的大小关系是______,理由:_________.
0
0
2.如图,∠1+∠2=180,∠1+∠3=180,∠2与∠3的大小关系是_________,理由:_______________.
A
C
D
B
0
0
1
2
3
∠A=∠BCD
同角的余角相等
∠2=∠3
同角的补角相等
3.如图,直线CD经过点O,且OC平分
∠AOB。∠AOD与∠BOD有怎样的大小关系?说明你的理由。
A
C
B
D
O
4、如图,
∠AOB=∠COD=90
°,则
∠AOC与∠BOD有怎样的大小关系?说
明你的理由。
1
2
3
A
C
B
D
O
互为余角
互为补角
图形
数量关系
性
质
1
2
∠1+∠2=90°
同角(或等角)的余角相等
1
2
∠1+∠2=180°
同角(或等角)的补角相等
这节课同学们有什么收获?
课堂检测
1.如果∠1=∠2,∠2=∠3,那么∠1 ∠3;
如果∠1>∠2,∠2>∠3,那么∠1 ∠3。
3.已知∠B是它补角的3倍,求∠B的度数。
2.已知∠A=28
30′,求∠A的余角、补角。
°
如图,O是直线AB上的一点,OC平分∠AOB,∠DOE=90o,则
(1)∠2=∠(
),∠1=∠(
)
(2)图中,互为余角的角共有哪几对?
(
)
(3)图中,∠DOB的补角是
。
4
3
∠1与∠2,∠1与∠4,∠2与∠3,∠4与∠3
∠1,∠3
A
1
4
3
2
B
C
D
E
O
F
(4)延长EO到F,∠COF与∠
BOD的大小关系怎样?
解:
∠COF=∠
BOD
理由:∵
∠COF+∠
3=1800
∠
BOD+∠1=1800
又∵∠
1
=
∠3
∴
∠COF=∠
BOD
思维拓展
同学们:再见!
知识就象一艘船
让它载着你
驶向理想的彼岸
初中数学七年级上册
(苏科版)
§6.3
余角、补角、对顶角
观察与思考
问:图中∠α与∠β的度数之间有怎样的关系?
α
β
1.如果两个角的和是一个直角,
那么这两个角互为余角,简称互余.
其中的一个角叫做另一个角的余角.
即∠α与∠β互为余角,
∠α的余角是∠β,
∠β的余角是∠α.
∠α+∠β=90°,
问:图中∠α与∠β的度数之间有怎样的关系?
观察与思考
α
β
2.如果两个角的和是一个平角,
那么这两个角互为补角,简称互补.
其中的一个角叫做另一个角的补角.
即∠α与∠β互为补角,
∠α的补角是∠β,
∠β的补角是∠α.
∠α+∠β=180°,
填表:看谁答的既快又准!
∠A的度数
50
n
(0<n<90)
∠A的余角
45
∠A的补角
120
0
0
0
0
40
0
130
0
135
0
45
0
60
0
30
0
90-n
0
0
180-n
0
0
判断:
1.如果∠1+∠2+∠3=90°,那么∠1、∠2、∠3这三个角称为互为余角(
)
2.两块直角三角板中∠A=90°,∠D=90°,则∠A与∠D互为补角。(
)
A
C
D
E
F
B
看谁反应快
错
对
3.一个角的补角一定比这个角大。
(
)
4.互补的两个角中,至少有一个角大于或等于直角(
)
5.两个互余的角都是锐角。(
)
对
错
对
看谁记的牢
1、如图,O为直线AB上一点,∠AOD=900,则图中哪些角互为余角?哪些角互为补角?
知识提升
如图,如果∠1与∠2互余,∠1与∠3互余,那么∠2与∠3相等吗?为什么?
1
2
3
同角的余角相等;
理由:∵∠1与∠
2互余,
∠1与∠3互余,
∴∠
2=
90
°
-
∠1,
∠3=
90
°
-
∠1
∴∠2=∠3
解:
∠2与∠3相等.
知识提升
如图,如果∠1与∠2互补,∠1与∠3互补,那么∠2与∠3的大小关系如何?说明你的理由。
1
2
3
同角的补角相等;
理由:∵∠1与∠
2互补,
∠1与∠3互补,
∴∠
2=
180
°
-
∠1,
∠3=
180
°
-
∠1
∴∠2=∠3
解:
∠2与∠3相等.
如果把互余改为互补,
∠2与∠4仍相等吗
如图,∠1和∠2互余,∠3和∠4互余,若∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
等角的余角相等
理由:∵∠1与∠2互余
∴∠2=90o-∠1
∵∠3与∠4互余
∴∠4=90o-∠3
又∵∠1=∠3
∴∠2=∠4
解:
∠2与∠4相等
等角的补角相等
余角性质:同角(或等角)的余角相等。
几何语言:
∵
∠1+
∠
2=900
∠
1+
∠
3
=
900
几何语言:
∵
∠1+
∠
2=900
∠
3+
∠
4
=
900
又∵
∠
1
=
∠
3
∴
∠
2
=
∠
3
(同角的余角相等)
∴
∠
2
=
∠
4
(等角的余角相等)
同角(或等角)的补角相等。
补角性质:
知识应用
1.如图,∠A+∠B=90,∠BCD+∠B=90,∠A与∠BCD的大小关系是______,理由:_________.
0
0
2.如图,∠1+∠2=180,∠1+∠3=180,∠2与∠3的大小关系是_________,理由:_______________.
A
C
D
B
0
0
1
2
3
∠A=∠BCD
同角的余角相等
∠2=∠3
同角的补角相等
3.如图,直线CD经过点O,且OC平分
∠AOB。∠AOD与∠BOD有怎样的大小关系?说明你的理由。
A
C
B
D
O
4、如图,
∠AOB=∠COD=90
°,则
∠AOC与∠BOD有怎样的大小关系?说
明你的理由。
1
2
3
A
C
B
D
O
互为余角
互为补角
图形
数量关系
性
质
1
2
∠1+∠2=90°
同角(或等角)的余角相等
1
2
∠1+∠2=180°
同角(或等角)的补角相等
这节课同学们有什么收获?
课堂检测
1.如果∠1=∠2,∠2=∠3,那么∠1 ∠3;
如果∠1>∠2,∠2>∠3,那么∠1 ∠3。
3.已知∠B是它补角的3倍,求∠B的度数。
2.已知∠A=28
30′,求∠A的余角、补角。
°
如图,O是直线AB上的一点,OC平分∠AOB,∠DOE=90o,则
(1)∠2=∠(
),∠1=∠(
)
(2)图中,互为余角的角共有哪几对?
(
)
(3)图中,∠DOB的补角是
。
4
3
∠1与∠2,∠1与∠4,∠2与∠3,∠4与∠3
∠1,∠3
A
1
4
3
2
B
C
D
E
O
F
(4)延长EO到F,∠COF与∠
BOD的大小关系怎样?
解:
∠COF=∠
BOD
理由:∵
∠COF+∠
3=1800
∠
BOD+∠1=1800
又∵∠
1
=
∠3
∴
∠COF=∠
BOD
思维拓展
同学们:再见!
知识就象一艘船
让它载着你
驶向理想的彼岸
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
