2019-2020学年山东省烟台市龙口市六年级(下)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2019-2020学年山东省烟台市龙口市六年级(下)期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 724.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 00:00:00 | ||
图片预览

文档简介
2019-2020学年山东省烟台市龙口市六年级(下)期末数学试卷(五四学制)
一、选择题(共12个小题,每小题3分,满分36分).
1.下列运算正确的是( )
A.x2 x4=x6
B.a8÷a2=a4
C.(﹣2x2)3=﹣6x6
D.(a﹣b)2=a2﹣b2
2.如图,从位置P到直线公路MN有四条小道,其中路程最短的是( )
A.PA
B.PB
C.PC
D.PD
3.空气是由多种气体混合而成,为了简明扼要地说明空气的组成情况,使用的统计图最好是( )
A.扇形统计图
B.条形统计图
C.折线统计图
D.频数分布直方图
4.下列问题中,采用的调查方式合适的是( )
A.对企业应聘人员进行面试,采用抽样调查方式
B.调查某品牌圆珠笔芯的使用寿命,采用普查方式
C.环保部门为调查渤海湾某部分水域的水质情况,采用抽样调查方式
D.了解龙口市城乡家庭的收入情况,采用普查方式
5.如图,C,D是线段AB上两点,若CB=5cm,DB=7cm,且D是AC的中点,则AB的长为( )
A.7cm
B.9cm
C.10cm
D.11cm
6.下列说法:①与同一条直线平行的两条直线必平行;②相等的角是对顶角:③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,没有交点的两条直线叫平行线,其中正确命题有( )个.
A.1
B.2
C.3
D.4
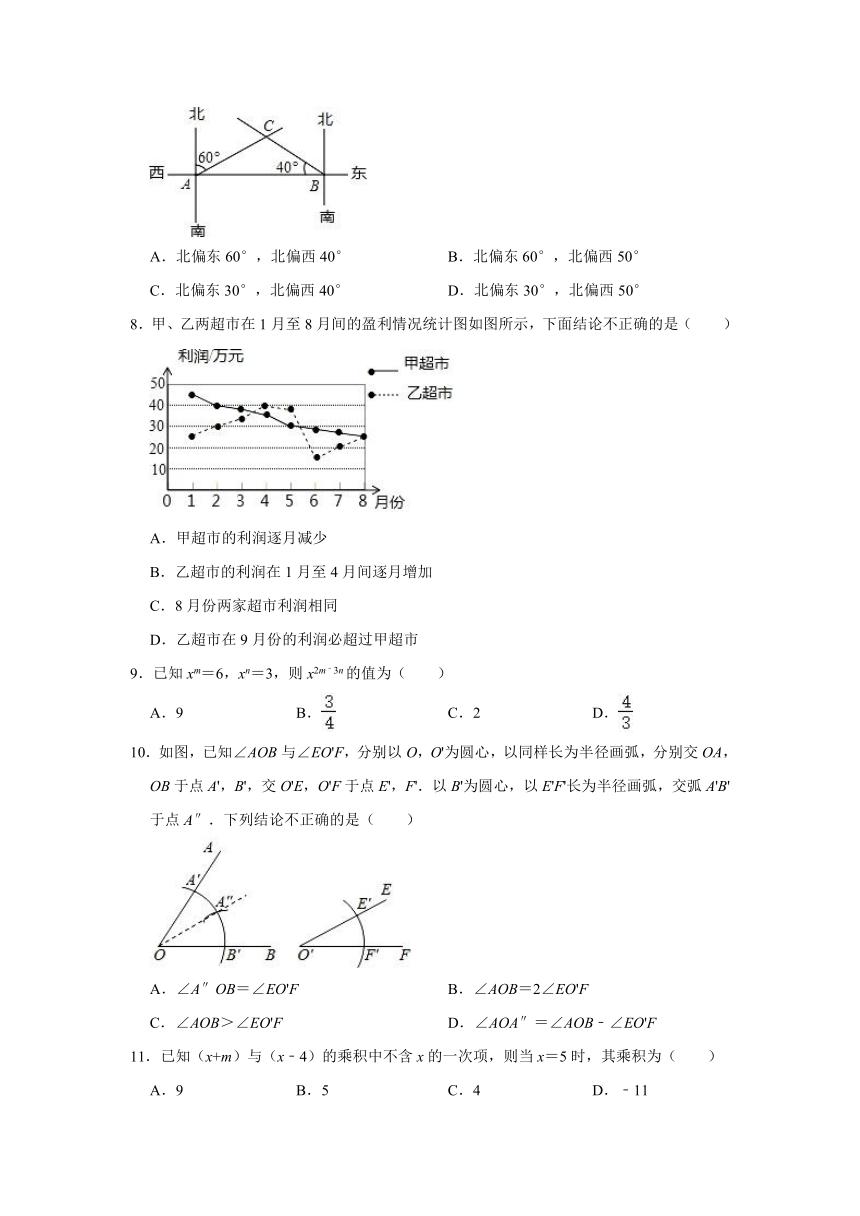
7.如图,在A、B两处观测到的C处的方向角分别是( )
A.北偏东60°,北偏西40°
B.北偏东60°,北偏西50°
C.北偏东30°,北偏西40°
D.北偏东30°,北偏西50°
8.甲、乙两超市在1月至8月间的盈利情况统计图如图所示,下面结论不正确的是( )
A.甲超市的利润逐月减少
B.乙超市的利润在1月至4月间逐月增加
C.8月份两家超市利润相同
D.乙超市在9月份的利润必超过甲超市
9.已知xm=6,xn=3,则x2m﹣3n的值为( )
A.9
B.
C.2
D.
10.如图,已知∠AOB与∠EO'F,分别以O,O'为圆心,以同样长为半径画弧,分别交OA,OB于点A',B',交O'E,O'F于点E',F'.以B'为圆心,以E'F'长为半径画弧,交弧A'B'于点A″.下列结论不正确的是( )
A.∠A″OB=∠EO'F
B.∠AOB=2∠EO'F
C.∠AOB>∠EO'F
D.∠AOA″=∠AOB﹣∠EO'F
11.已知(x+m)与(x﹣4)的乘积中不含x的一次项,则当x=5时,其乘积为( )
A.9
B.5
C.4
D.﹣11
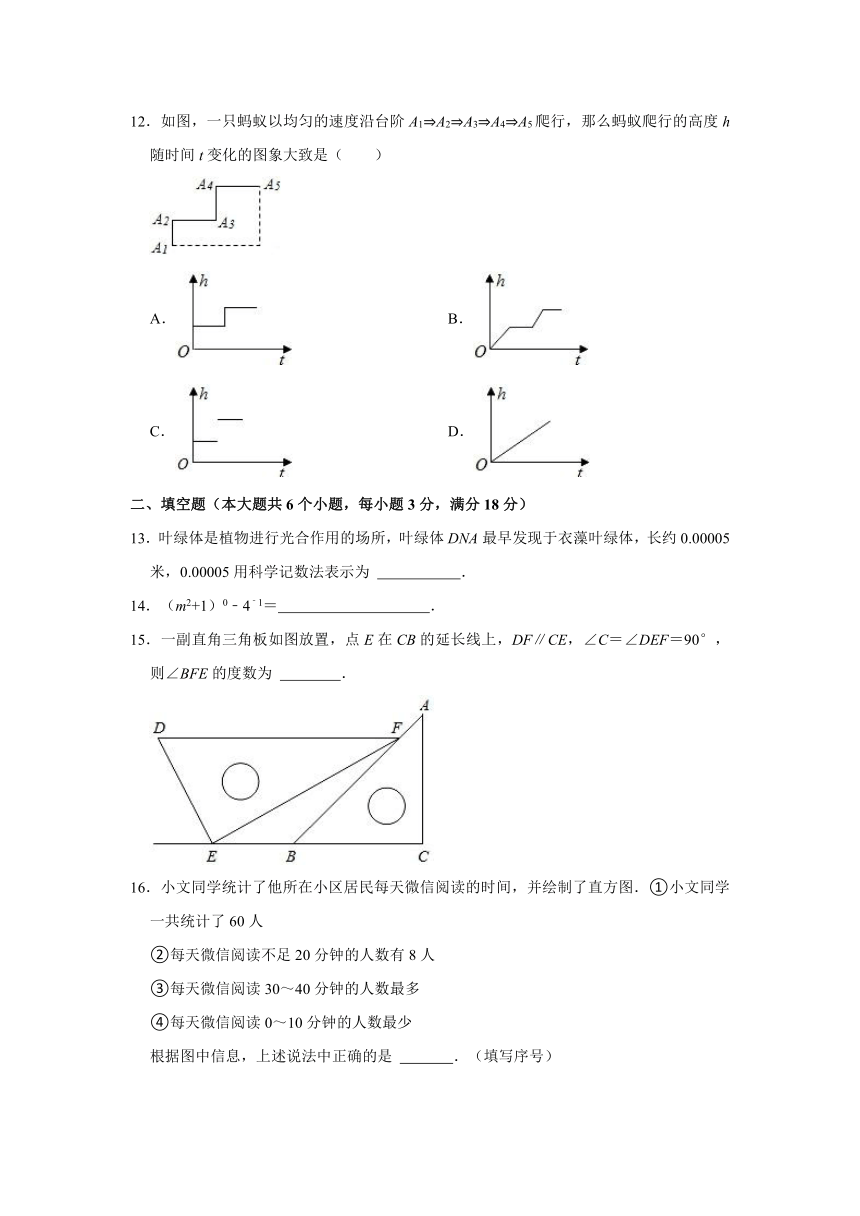
12.如图,一只蚂蚁以均匀的速度沿台阶A1 A2 A3 A4 A5爬行,那么蚂蚁爬行的高度h随时间t变化的图象大致是( )
A.
B.
C.
D.
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.叶绿体是植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米,0.00005用科学记数法表示为
.
14.(m2+1)0﹣4﹣1=
.
15.一副直角三角板如图放置,点E在CB的延长线上,DF∥CE,∠C=∠DEF=90°,则∠BFE的度数为
.
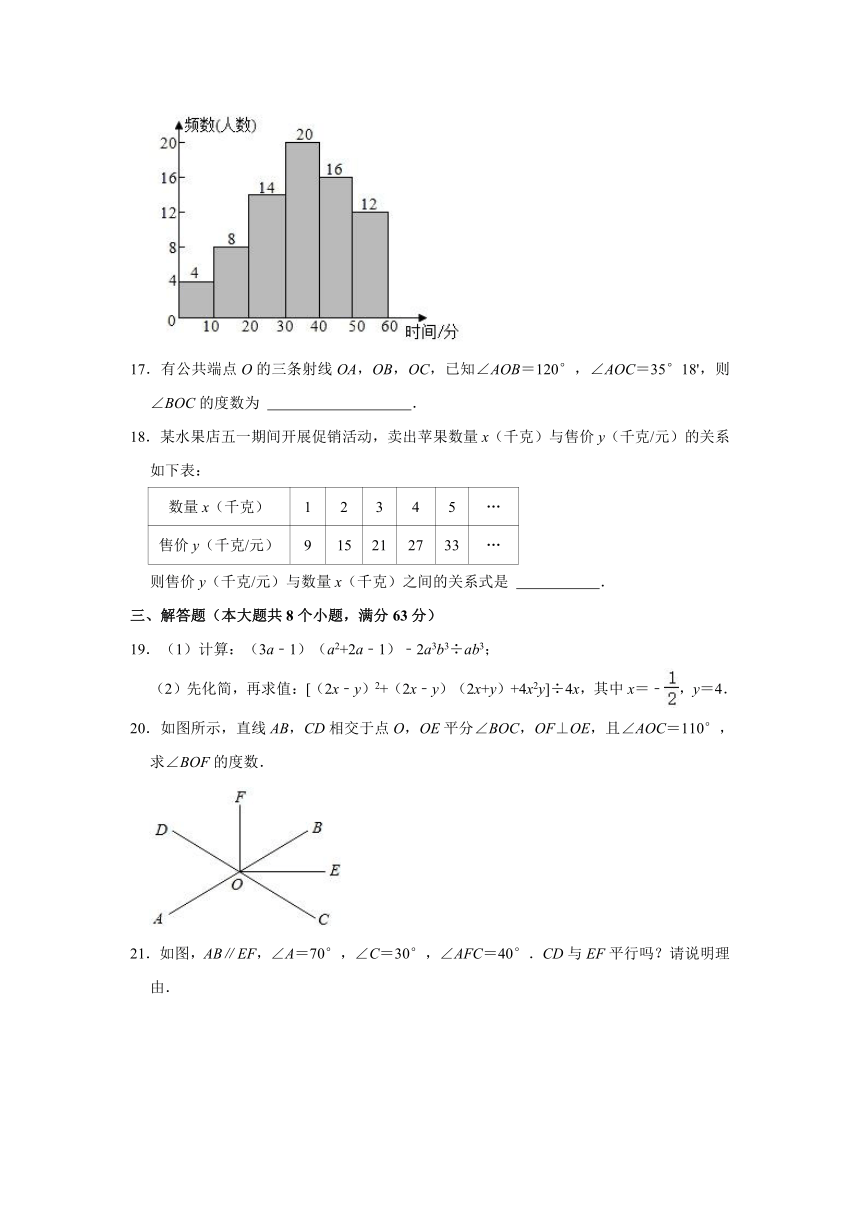
16.小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.①小文同学一共统计了60人
②每天微信阅读不足20分钟的人数有8人
③每天微信阅读30~40分钟的人数最多
④每天微信阅读0~10分钟的人数最少
根据图中信息,上述说法中正确的是
.(填写序号)
17.有公共端点O的三条射线OA,OB,OC,已知∠AOB=120°,∠AOC=35°18',则∠BOC的度数为
.
18.某水果店五一期间开展促销活动,卖出苹果数量x(千克)与售价y(千克/元)的关系如下表:
数量x(千克)
1
2
3
4
5
…
售价y(千克/元)
9
15
21
27
33
…
则售价y(千克/元)与数量x(千克)之间的关系式是
.
三、解答题(本大题共8个小题,满分63分)
19.(1)计算:(3a﹣1)(a2+2a﹣1)﹣2a3b3÷ab3;
(2)先化简,再求值:[(2x﹣y)2+(2x﹣y)(2x+y)+4x2y]÷4x,其中x=﹣,y=4.
20.如图所示,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOC=110°,求∠BOF的度数.
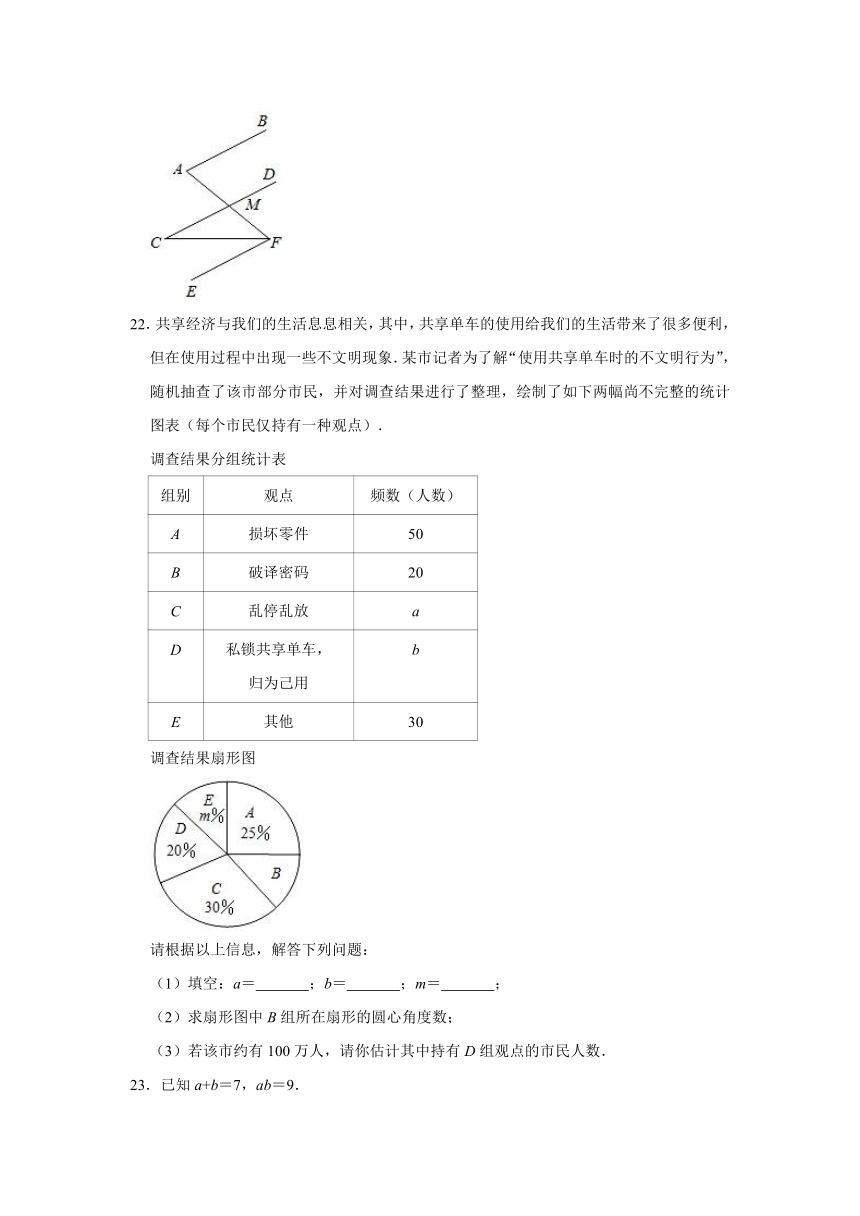
21.如图,AB∥EF,∠A=70°,∠C=30°,∠AFC=40°.CD与EF平行吗?请说明理由.
22.共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利,但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”,随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别
观点
频数(人数)
A
损坏零件
50
B
破译密码
20
C
乱停乱放
a
D
私锁共享单车,归为己用
b
E
其他
30
调查结果扇形图
请根据以上信息,解答下列问题:
(1)填空:a=
;b=
;m=
;
(2)求扇形图中B组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有D组观点的市民人数.
23.已知a+b=7,ab=9.
(1)求a2+b2的值;
(2)如图,若a,b分别是两个正方形的边长,求图中阴影部分的面积.
24.规定两个非零数a,b之间的一种新运算,如果am=b,那么a※b=m.
例如:因为52=25,所以5※25=2;因为50=1,所以5※1=0.
(1)根据上述规定填空:2※16=
;3※=
.
(2)在运算时,按以上规定请说明等式8※9+8※10=8※90成立.
25.周末,小明骑自行车去外婆家,从家出发30分钟后到达甲地,在甲地停车游玩了一段时间后,按原速继续骑行前进,小明离家1小时后,妈妈骑电动车沿小明骑自行车的路线追赶小明,如图是他们离家的路程y(千米)与小明离家时间x(小时)的关系图,已知妈妈骑电动车的速度是小明骑自行车速度的3倍.
(1)小明在甲地游玩时间是
小时;小明骑自行车的速度是
千米/小时;妈妈骑电动车的速度是
千米/小时;
(2)若妈妈与小明同时到达外婆家,求小明家到外婆家的路程及两人分别骑行的时间.
26.如图,已知AB∥CD,点M为平面内一点,AM⊥DM于点M.
(1)如图1,过点M作MG⊥AB于点G,延长GM交CD于N,请说明∠AMG=∠MDC;
(2)如图2,在(1)问的条件下,点E,F分别在GB上,连接ME,MF,DF.已知ME平分∠AMG,MF平分∠GMD,若∠FDM+∠CDF=180°,∠MFD=3∠GME,求∠GME的度数.
参考答案
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1.下列运算正确的是( )
A.x2 x4=x6
B.a8÷a2=a4
C.(﹣2x2)3=﹣6x6
D.(a﹣b)2=a2﹣b2
解:A.根据同底数幂的乘法,得x2 x4=x6,故A符合题意.
B.根据同底数幂的除法,得a8÷a2=a6,故B不符合题意.
C.根据积的乘方以及幂的乘方,得(﹣2x2)3=﹣8x6,故C不符合题意.
D.根据完全平方公式,得(a﹣b)2=a2+b2﹣2ab,故D不符合题意.
故选:A.
2.如图,从位置P到直线公路MN有四条小道,其中路程最短的是( )
A.PA
B.PB
C.PC
D.PD
解:根据垂线段最短得,能最快到达公路MN的小道是PB,
故选:B.
3.空气是由多种气体混合而成,为了简明扼要地说明空气的组成情况,使用的统计图最好是( )
A.扇形统计图
B.条形统计图
C.折线统计图
D.频数分布直方图
解:为了简明扼要地说明空气的组成情况,使用的统计图最好是扇形统计图,
故选:A.
4.下列问题中,采用的调查方式合适的是( )
A.对企业应聘人员进行面试,采用抽样调查方式
B.调查某品牌圆珠笔芯的使用寿命,采用普查方式
C.环保部门为调查渤海湾某部分水域的水质情况,采用抽样调查方式
D.了解龙口市城乡家庭的收入情况,采用普查方式
解:A.对企业应聘人员进行面试,适合采用全面调查方式,故本选项不合题意;
B.调查某品牌圆珠笔芯的使用寿命,适合采用抽样调查方式,故本选项不合题意;
C.环保部门为调查渤海湾某部分水域的水质情况,适合采用抽样调查方式,故本选项符合题意;
D.了解龙口市城乡家庭的收入情况,适合采用抽样调查方式,故本选项不合题意;
故选:C.
5.如图,C,D是线段AB上两点,若CB=5cm,DB=7cm,且D是AC的中点,则AB的长为( )
A.7cm
B.9cm
C.10cm
D.11cm
解:∵CB=5cm,DB=7cm,
∴CD=BD﹣BC=7﹣5=2cm,
∵D是AC的中点,
∴AD=CD=2cm,
∵AB=AD+CD+BC=2+2+5=9cm,
故选:B.
6.下列说法:①与同一条直线平行的两条直线必平行;②相等的角是对顶角:③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,没有交点的两条直线叫平行线,其中正确命题有( )个.
A.1
B.2
C.3
D.4
解:与同一条直线平行的两条直线必平行,①说法正确;
相等的角不一定是对顶角,②说法错误;
在同一平面内过一点且有且只有一条直线与已知直线垂直,③说法正确;
④在同一平面内,不相交的两条直线叫平行线,④说法正确;
正确的有3个,
故选:C.
7.如图,在A、B两处观测到的C处的方向角分别是( )
A.北偏东60°,北偏西40°
B.北偏东60°,北偏西50°
C.北偏东30°,北偏西40°
D.北偏东30°,北偏西50°
解:A处观测到的C处的方向角是:北偏东60°,
B处观测到的C处的方向角是:北偏西50°.
故选:B.
8.甲、乙两超市在1月至8月间的盈利情况统计图如图所示,下面结论不正确的是( )
A.甲超市的利润逐月减少
B.乙超市的利润在1月至4月间逐月增加
C.8月份两家超市利润相同
D.乙超市在9月份的利润必超过甲超市
解:A、甲超市的利润逐月减少,此选项正确;
B、乙超市的利润在1月至4月间逐月增加,此选项正确;
C、8月份两家超市利润相同,此选项正确;
D、乙超市在9月份的利润不一定超过甲超市,此选项错误;
故选:D.
9.已知xm=6,xn=3,则x2m﹣3n的值为( )
A.9
B.
C.2
D.
解:x2m﹣3n====.
故选:D.
10.如图,已知∠AOB与∠EO'F,分别以O,O'为圆心,以同样长为半径画弧,分别交OA,OB于点A',B',交O'E,O'F于点E',F'.以B'为圆心,以E'F'长为半径画弧,交弧A'B'于点A″.下列结论不正确的是( )
A.∠A″OB=∠EO'F
B.∠AOB=2∠EO'F
C.∠AOB>∠EO'F
D.∠AOA″=∠AOB﹣∠EO'F
解:由作图可知,∠A″OB=∠EO′F,∠AOB>∠EOF,∠AOA′=∠AOB﹣∠A″OB=∠AOB﹣∠EO′F,
故选项A,C,D正确,
故选:B.
11.已知(x+m)与(x﹣4)的乘积中不含x的一次项,则当x=5时,其乘积为( )
A.9
B.5
C.4
D.﹣11
解:(x+m)(x﹣4)
=x2+mx﹣4x﹣4m
=x2+(m﹣4)x﹣4m,
∵(x+m)与(x﹣4)的乘积中不含x的一次项,
∴m﹣4=0,
解得m=4,
∴当x=5时,(x+m)(x﹣4)=(5+4)(5﹣4)=9.
故选:A.
12.如图,一只蚂蚁以均匀的速度沿台阶A1 A2 A3 A4 A5爬行,那么蚂蚁爬行的高度h随时间t变化的图象大致是( )
A.
B.
C.
D.
解:因为蚂蚁以均匀的速度沿台阶A1 A2 A3 A4 A5爬行,从A1 A2的过程中,高度随时间匀速上升,从A2 A3的过程,高度不变,从A3 A4的过程,高度随时间匀速上升,从A4 A5的过程中,高度不变,
所以蚂蚁爬行的高度h随时间t变化的图象是B.
故选:B.
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.叶绿体是植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米,0.00005用科学记数法表示为
5×10﹣5 .
解:0.00005=5×10﹣5.
故答案为:5×10﹣5.
14.(m2+1)0﹣4﹣1= .
解:∵m2+1≠0,
∴原式=1﹣
=,
故答案为:.
15.一副直角三角板如图放置,点E在CB的延长线上,DF∥CE,∠C=∠DEF=90°,则∠BFE的度数为
15° .
解:由题意得:∠DFE=30°,∠ABC=45°.
∵DF∥CE,
∴∠FEB=∠DFE=30°.
又∵∠BFE+∠FEB=∠ABC,
∴∠BFE=∠ABC﹣∠FEB=45°﹣30°=15°.
故答案为:15°.
16.小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.①小文同学一共统计了60人
②每天微信阅读不足20分钟的人数有8人
③每天微信阅读30~40分钟的人数最多
④每天微信阅读0~10分钟的人数最少
根据图中信息,上述说法中正确的是
③④ .(填写序号)
解:由直方图可得,
小文同学一共统计了:4+8+14+20+16+12=74(人),故①错误;
每天微信阅读不足20分钟的有4+8=12(人),故②错误;
每天微信阅读30~40分钟的人数最多,故③正确;
每天微信阅读0~10分钟的人数最少,故④正确;
故答案为:③④.
17.有公共端点O的三条射线OA,OB,OC,已知∠AOB=120°,∠AOC=35°18',则∠BOC的度数为
84°42'或155°18' .
解:当射线OC在∠AOB内部时,
∠BOC=∠AOB﹣∠AOC
=120°﹣35°18'
=84°42′;
当射线OC在∠AOB外部时,
∠BOC=∠AOB+∠AOC
=120°+35°18'
=155°18′.
故答案为:84°42′或155°18′.
18.某水果店五一期间开展促销活动,卖出苹果数量x(千克)与售价y(千克/元)的关系如下表:
数量x(千克)
1
2
3
4
5
…
售价y(千克/元)
9
15
21
27
33
…
则售价y(千克/元)与数量x(千克)之间的关系式是
y=6x+3 .
解:9=6×1+3,
15=6×2+3,
21=6×3+3,
27=6×4+3,
…
∴y=6x+3,
故答案为:y=6x+3.
三、解答题(本大题共8个小题,满分63分)
19.(1)计算:(3a﹣1)(a2+2a﹣1)﹣2a3b3÷ab3;
(2)先化简,再求值:[(2x﹣y)2+(2x﹣y)(2x+y)+4x2y]÷4x,其中x=﹣,y=4.
解:(1)原式=3a3+6a2﹣3a﹣a2﹣2a+1﹣2a2
=3a3+3a2﹣5a+1;
(2)原式=[4x2﹣4xy+y2+4x2﹣y2+4x2y]÷4x
=(8x2﹣4xy+4x2y)÷4x
=2x﹣y+xy,
当x=﹣,y=4时,原式=﹣1﹣4﹣2=﹣7.
20.如图所示,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOC=110°,求∠BOF的度数.
解:∵∠AOC=110°,
∴∠BOC=70°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=35°,
∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=∠EOF ∠BOE=90° 35°=55°.
21.如图,AB∥EF,∠A=70°,∠C=30°,∠AFC=40°.CD与EF平行吗?请说明理由.
解:CD∥EF,理由如下:
∵AB∥EF,∠A=70°,
∴∠AFE=∠A=70°,
∵∠AFC=40°,
∴∠EFC=∠AFE﹣∠AFC=70°﹣40°=30°,
∵∠C=30°,
∴∠EFC=∠C,
∴CD∥EF.
22.共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利,但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”,随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别
观点
频数(人数)
A
损坏零件
50
B
破译密码
20
C
乱停乱放
a
D
私锁共享单车,归为己用
b
E
其他
30
调查结果扇形图
请根据以上信息,解答下列问题:
(1)填空:a= 60 ;b= 40 ;m= 15 ;
(2)求扇形图中B组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有D组观点的市民人数.
解:(1)50÷25%=200人,c=200×30%=60人,b=200×20%=40人,30÷200=15%,
故答案为:60;40;15;
(2)360°×(1﹣25%﹣30%﹣20%﹣15%)=36°;
答:扇形图中B组所在扇形的圆心角度数为36°.
(3)100×20%=20(万人)
答:持有D组观点的市民人数大约为20万人,
23.已知a+b=7,ab=9.
(1)求a2+b2的值;
(2)如图,若a,b分别是两个正方形的边长,求图中阴影部分的面积.
解:(1)∵a+b=7,ab=9,
∴(a+b)2=a2+b2+2ab=49.
∴a2+b2+18=49.
∴a2+b2=31.
(2)由图知:S阴影=S大正方形﹣S空白=.
∴S阴影====.
24.规定两个非零数a,b之间的一种新运算,如果am=b,那么a※b=m.
例如:因为52=25,所以5※25=2;因为50=1,所以5※1=0.
(1)根据上述规定填空:2※16= 4 ;3※= ﹣3 .
(2)在运算时,按以上规定请说明等式8※9+8※10=8※90成立.
解:(1)∵24=16,
∴2※16=4;
∵,
∴3※=﹣3.
故答案为:4;﹣3;
(2)设8※9=x,8※10=y,则8x=9,8y=10,
8x×8y=8x+y=90,
∴8※90=x+y,
∵8※9+8※10=x+y,
∴8※9+8※10=8※90.
25.周末,小明骑自行车去外婆家,从家出发30分钟后到达甲地,在甲地停车游玩了一段时间后,按原速继续骑行前进,小明离家1小时后,妈妈骑电动车沿小明骑自行车的路线追赶小明,如图是他们离家的路程y(千米)与小明离家时间x(小时)的关系图,已知妈妈骑电动车的速度是小明骑自行车速度的3倍.
(1)小明在甲地游玩时间是
小时;小明骑自行车的速度是
12 千米/小时;妈妈骑电动车的速度是
36 千米/小时;
(2)若妈妈与小明同时到达外婆家,求小明家到外婆家的路程及两人分别骑行的时间.
解:(1)由图象可得,
小明在甲地游玩时间是﹣0.5===(小时),
小明骑自行车的速度是:6÷0.5=12(千米/小时),妈妈骑电动车的速度是12×3=36(千米/小时),
故答案为:,12,36;
(2)设小明家到外婆家的路程为S千米,
+(1﹣),
解得S=12,
∴小明骑行的时间为0.5×2=1(小时),妈妈骑行的时间为=(小时),
答:小明家到外婆家的路程是12千米,小明骑行的时间为1小时,妈妈骑行的时间为小时.
26.如图,已知AB∥CD,点M为平面内一点,AM⊥DM于点M.
(1)如图1,过点M作MG⊥AB于点G,延长GM交CD于N,请说明∠AMG=∠MDC;
(2)如图2,在(1)问的条件下,点E,F分别在GB上,连接ME,MF,DF.已知ME平分∠AMG,MF平分∠GMD,若∠FDM+∠CDF=180°,∠MFD=3∠GME,求∠GME的度数.
解:(1)∵AM⊥MD,
∴∠AMD=90°.
∴∠AMG+∠DMN=180°﹣∠AMD=90°,
∵MG⊥AB,AB∥CD,
∴GN⊥CD,
∴∠MND=90°,
∴∠DMN+∠D=180°﹣∠MND=90°,
∴∠AMG=∠MDC.
(2)∵ME平分∠AMG,MF平分∠GMD,
∴∠GME=∠AME,∠GMF=∠DMF=∠GMD,
设∠GME=x,则∠AME=x,∠MDC=2x,∠MFD=3∠GME=3x,∠GMD=∠AMG+∠AMD=90°+2x,
∴∠GMF=(90°+2x)=45°+x,
∵AB∥CD,
∴∠GFD+∠CDF=180°,
∵∠FDM+∠CDF=180°,
∴∠GFD=∠FDM,
∴2∠GFD+∠CDM=180°,
∴∠GFD=(180°﹣∠CDM)=(180°﹣2x)=90°﹣x,
∴∠MFG=∠GFD﹣∠MFD=90°﹣x﹣3x=90°﹣4x,
在直角三角形GMF中,∠MFG+∠GMF=90°,
∴90o﹣4x+45o+x=90o,
∴x=15o,
∴∠GME=15°.
一、选择题(共12个小题,每小题3分,满分36分).
1.下列运算正确的是( )
A.x2 x4=x6
B.a8÷a2=a4
C.(﹣2x2)3=﹣6x6
D.(a﹣b)2=a2﹣b2
2.如图,从位置P到直线公路MN有四条小道,其中路程最短的是( )
A.PA
B.PB
C.PC
D.PD
3.空气是由多种气体混合而成,为了简明扼要地说明空气的组成情况,使用的统计图最好是( )
A.扇形统计图
B.条形统计图
C.折线统计图
D.频数分布直方图
4.下列问题中,采用的调查方式合适的是( )
A.对企业应聘人员进行面试,采用抽样调查方式
B.调查某品牌圆珠笔芯的使用寿命,采用普查方式
C.环保部门为调查渤海湾某部分水域的水质情况,采用抽样调查方式
D.了解龙口市城乡家庭的收入情况,采用普查方式
5.如图,C,D是线段AB上两点,若CB=5cm,DB=7cm,且D是AC的中点,则AB的长为( )
A.7cm
B.9cm
C.10cm
D.11cm
6.下列说法:①与同一条直线平行的两条直线必平行;②相等的角是对顶角:③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,没有交点的两条直线叫平行线,其中正确命题有( )个.
A.1
B.2
C.3
D.4
7.如图,在A、B两处观测到的C处的方向角分别是( )
A.北偏东60°,北偏西40°
B.北偏东60°,北偏西50°
C.北偏东30°,北偏西40°
D.北偏东30°,北偏西50°
8.甲、乙两超市在1月至8月间的盈利情况统计图如图所示,下面结论不正确的是( )
A.甲超市的利润逐月减少
B.乙超市的利润在1月至4月间逐月增加
C.8月份两家超市利润相同
D.乙超市在9月份的利润必超过甲超市
9.已知xm=6,xn=3,则x2m﹣3n的值为( )
A.9
B.
C.2
D.
10.如图,已知∠AOB与∠EO'F,分别以O,O'为圆心,以同样长为半径画弧,分别交OA,OB于点A',B',交O'E,O'F于点E',F'.以B'为圆心,以E'F'长为半径画弧,交弧A'B'于点A″.下列结论不正确的是( )
A.∠A″OB=∠EO'F
B.∠AOB=2∠EO'F
C.∠AOB>∠EO'F
D.∠AOA″=∠AOB﹣∠EO'F
11.已知(x+m)与(x﹣4)的乘积中不含x的一次项,则当x=5时,其乘积为( )
A.9
B.5
C.4
D.﹣11
12.如图,一只蚂蚁以均匀的速度沿台阶A1 A2 A3 A4 A5爬行,那么蚂蚁爬行的高度h随时间t变化的图象大致是( )
A.
B.
C.
D.
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.叶绿体是植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米,0.00005用科学记数法表示为
.
14.(m2+1)0﹣4﹣1=
.
15.一副直角三角板如图放置,点E在CB的延长线上,DF∥CE,∠C=∠DEF=90°,则∠BFE的度数为
.
16.小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.①小文同学一共统计了60人
②每天微信阅读不足20分钟的人数有8人
③每天微信阅读30~40分钟的人数最多
④每天微信阅读0~10分钟的人数最少
根据图中信息,上述说法中正确的是
.(填写序号)
17.有公共端点O的三条射线OA,OB,OC,已知∠AOB=120°,∠AOC=35°18',则∠BOC的度数为
.
18.某水果店五一期间开展促销活动,卖出苹果数量x(千克)与售价y(千克/元)的关系如下表:
数量x(千克)
1
2
3
4
5
…
售价y(千克/元)
9
15
21
27
33
…
则售价y(千克/元)与数量x(千克)之间的关系式是
.
三、解答题(本大题共8个小题,满分63分)
19.(1)计算:(3a﹣1)(a2+2a﹣1)﹣2a3b3÷ab3;
(2)先化简,再求值:[(2x﹣y)2+(2x﹣y)(2x+y)+4x2y]÷4x,其中x=﹣,y=4.
20.如图所示,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOC=110°,求∠BOF的度数.
21.如图,AB∥EF,∠A=70°,∠C=30°,∠AFC=40°.CD与EF平行吗?请说明理由.
22.共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利,但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”,随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别
观点
频数(人数)
A
损坏零件
50
B
破译密码
20
C
乱停乱放
a
D
私锁共享单车,归为己用
b
E
其他
30
调查结果扇形图
请根据以上信息,解答下列问题:
(1)填空:a=
;b=
;m=
;
(2)求扇形图中B组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有D组观点的市民人数.
23.已知a+b=7,ab=9.
(1)求a2+b2的值;
(2)如图,若a,b分别是两个正方形的边长,求图中阴影部分的面积.
24.规定两个非零数a,b之间的一种新运算,如果am=b,那么a※b=m.
例如:因为52=25,所以5※25=2;因为50=1,所以5※1=0.
(1)根据上述规定填空:2※16=
;3※=
.
(2)在运算时,按以上规定请说明等式8※9+8※10=8※90成立.
25.周末,小明骑自行车去外婆家,从家出发30分钟后到达甲地,在甲地停车游玩了一段时间后,按原速继续骑行前进,小明离家1小时后,妈妈骑电动车沿小明骑自行车的路线追赶小明,如图是他们离家的路程y(千米)与小明离家时间x(小时)的关系图,已知妈妈骑电动车的速度是小明骑自行车速度的3倍.
(1)小明在甲地游玩时间是
小时;小明骑自行车的速度是
千米/小时;妈妈骑电动车的速度是
千米/小时;
(2)若妈妈与小明同时到达外婆家,求小明家到外婆家的路程及两人分别骑行的时间.
26.如图,已知AB∥CD,点M为平面内一点,AM⊥DM于点M.
(1)如图1,过点M作MG⊥AB于点G,延长GM交CD于N,请说明∠AMG=∠MDC;
(2)如图2,在(1)问的条件下,点E,F分别在GB上,连接ME,MF,DF.已知ME平分∠AMG,MF平分∠GMD,若∠FDM+∠CDF=180°,∠MFD=3∠GME,求∠GME的度数.
参考答案
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1.下列运算正确的是( )
A.x2 x4=x6
B.a8÷a2=a4
C.(﹣2x2)3=﹣6x6
D.(a﹣b)2=a2﹣b2
解:A.根据同底数幂的乘法,得x2 x4=x6,故A符合题意.
B.根据同底数幂的除法,得a8÷a2=a6,故B不符合题意.
C.根据积的乘方以及幂的乘方,得(﹣2x2)3=﹣8x6,故C不符合题意.
D.根据完全平方公式,得(a﹣b)2=a2+b2﹣2ab,故D不符合题意.
故选:A.
2.如图,从位置P到直线公路MN有四条小道,其中路程最短的是( )
A.PA
B.PB
C.PC
D.PD
解:根据垂线段最短得,能最快到达公路MN的小道是PB,
故选:B.
3.空气是由多种气体混合而成,为了简明扼要地说明空气的组成情况,使用的统计图最好是( )
A.扇形统计图
B.条形统计图
C.折线统计图
D.频数分布直方图
解:为了简明扼要地说明空气的组成情况,使用的统计图最好是扇形统计图,
故选:A.
4.下列问题中,采用的调查方式合适的是( )
A.对企业应聘人员进行面试,采用抽样调查方式
B.调查某品牌圆珠笔芯的使用寿命,采用普查方式
C.环保部门为调查渤海湾某部分水域的水质情况,采用抽样调查方式
D.了解龙口市城乡家庭的收入情况,采用普查方式
解:A.对企业应聘人员进行面试,适合采用全面调查方式,故本选项不合题意;
B.调查某品牌圆珠笔芯的使用寿命,适合采用抽样调查方式,故本选项不合题意;
C.环保部门为调查渤海湾某部分水域的水质情况,适合采用抽样调查方式,故本选项符合题意;
D.了解龙口市城乡家庭的收入情况,适合采用抽样调查方式,故本选项不合题意;
故选:C.
5.如图,C,D是线段AB上两点,若CB=5cm,DB=7cm,且D是AC的中点,则AB的长为( )
A.7cm
B.9cm
C.10cm
D.11cm
解:∵CB=5cm,DB=7cm,
∴CD=BD﹣BC=7﹣5=2cm,
∵D是AC的中点,
∴AD=CD=2cm,
∵AB=AD+CD+BC=2+2+5=9cm,
故选:B.
6.下列说法:①与同一条直线平行的两条直线必平行;②相等的角是对顶角:③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,没有交点的两条直线叫平行线,其中正确命题有( )个.
A.1
B.2
C.3
D.4
解:与同一条直线平行的两条直线必平行,①说法正确;
相等的角不一定是对顶角,②说法错误;
在同一平面内过一点且有且只有一条直线与已知直线垂直,③说法正确;
④在同一平面内,不相交的两条直线叫平行线,④说法正确;
正确的有3个,
故选:C.
7.如图,在A、B两处观测到的C处的方向角分别是( )
A.北偏东60°,北偏西40°
B.北偏东60°,北偏西50°
C.北偏东30°,北偏西40°
D.北偏东30°,北偏西50°
解:A处观测到的C处的方向角是:北偏东60°,
B处观测到的C处的方向角是:北偏西50°.
故选:B.
8.甲、乙两超市在1月至8月间的盈利情况统计图如图所示,下面结论不正确的是( )
A.甲超市的利润逐月减少
B.乙超市的利润在1月至4月间逐月增加
C.8月份两家超市利润相同
D.乙超市在9月份的利润必超过甲超市
解:A、甲超市的利润逐月减少,此选项正确;
B、乙超市的利润在1月至4月间逐月增加,此选项正确;
C、8月份两家超市利润相同,此选项正确;
D、乙超市在9月份的利润不一定超过甲超市,此选项错误;
故选:D.
9.已知xm=6,xn=3,则x2m﹣3n的值为( )
A.9
B.
C.2
D.
解:x2m﹣3n====.
故选:D.
10.如图,已知∠AOB与∠EO'F,分别以O,O'为圆心,以同样长为半径画弧,分别交OA,OB于点A',B',交O'E,O'F于点E',F'.以B'为圆心,以E'F'长为半径画弧,交弧A'B'于点A″.下列结论不正确的是( )
A.∠A″OB=∠EO'F
B.∠AOB=2∠EO'F
C.∠AOB>∠EO'F
D.∠AOA″=∠AOB﹣∠EO'F
解:由作图可知,∠A″OB=∠EO′F,∠AOB>∠EOF,∠AOA′=∠AOB﹣∠A″OB=∠AOB﹣∠EO′F,
故选项A,C,D正确,
故选:B.
11.已知(x+m)与(x﹣4)的乘积中不含x的一次项,则当x=5时,其乘积为( )
A.9
B.5
C.4
D.﹣11
解:(x+m)(x﹣4)
=x2+mx﹣4x﹣4m
=x2+(m﹣4)x﹣4m,
∵(x+m)与(x﹣4)的乘积中不含x的一次项,
∴m﹣4=0,
解得m=4,
∴当x=5时,(x+m)(x﹣4)=(5+4)(5﹣4)=9.
故选:A.
12.如图,一只蚂蚁以均匀的速度沿台阶A1 A2 A3 A4 A5爬行,那么蚂蚁爬行的高度h随时间t变化的图象大致是( )
A.
B.
C.
D.
解:因为蚂蚁以均匀的速度沿台阶A1 A2 A3 A4 A5爬行,从A1 A2的过程中,高度随时间匀速上升,从A2 A3的过程,高度不变,从A3 A4的过程,高度随时间匀速上升,从A4 A5的过程中,高度不变,
所以蚂蚁爬行的高度h随时间t变化的图象是B.
故选:B.
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.叶绿体是植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米,0.00005用科学记数法表示为
5×10﹣5 .
解:0.00005=5×10﹣5.
故答案为:5×10﹣5.
14.(m2+1)0﹣4﹣1= .
解:∵m2+1≠0,
∴原式=1﹣
=,
故答案为:.
15.一副直角三角板如图放置,点E在CB的延长线上,DF∥CE,∠C=∠DEF=90°,则∠BFE的度数为
15° .
解:由题意得:∠DFE=30°,∠ABC=45°.
∵DF∥CE,
∴∠FEB=∠DFE=30°.
又∵∠BFE+∠FEB=∠ABC,
∴∠BFE=∠ABC﹣∠FEB=45°﹣30°=15°.
故答案为:15°.
16.小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.①小文同学一共统计了60人
②每天微信阅读不足20分钟的人数有8人
③每天微信阅读30~40分钟的人数最多
④每天微信阅读0~10分钟的人数最少
根据图中信息,上述说法中正确的是
③④ .(填写序号)
解:由直方图可得,
小文同学一共统计了:4+8+14+20+16+12=74(人),故①错误;
每天微信阅读不足20分钟的有4+8=12(人),故②错误;
每天微信阅读30~40分钟的人数最多,故③正确;
每天微信阅读0~10分钟的人数最少,故④正确;
故答案为:③④.
17.有公共端点O的三条射线OA,OB,OC,已知∠AOB=120°,∠AOC=35°18',则∠BOC的度数为
84°42'或155°18' .
解:当射线OC在∠AOB内部时,
∠BOC=∠AOB﹣∠AOC
=120°﹣35°18'
=84°42′;
当射线OC在∠AOB外部时,
∠BOC=∠AOB+∠AOC
=120°+35°18'
=155°18′.
故答案为:84°42′或155°18′.
18.某水果店五一期间开展促销活动,卖出苹果数量x(千克)与售价y(千克/元)的关系如下表:
数量x(千克)
1
2
3
4
5
…
售价y(千克/元)
9
15
21
27
33
…
则售价y(千克/元)与数量x(千克)之间的关系式是
y=6x+3 .
解:9=6×1+3,
15=6×2+3,
21=6×3+3,
27=6×4+3,
…
∴y=6x+3,
故答案为:y=6x+3.
三、解答题(本大题共8个小题,满分63分)
19.(1)计算:(3a﹣1)(a2+2a﹣1)﹣2a3b3÷ab3;
(2)先化简,再求值:[(2x﹣y)2+(2x﹣y)(2x+y)+4x2y]÷4x,其中x=﹣,y=4.
解:(1)原式=3a3+6a2﹣3a﹣a2﹣2a+1﹣2a2
=3a3+3a2﹣5a+1;
(2)原式=[4x2﹣4xy+y2+4x2﹣y2+4x2y]÷4x
=(8x2﹣4xy+4x2y)÷4x
=2x﹣y+xy,
当x=﹣,y=4时,原式=﹣1﹣4﹣2=﹣7.
20.如图所示,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOC=110°,求∠BOF的度数.
解:∵∠AOC=110°,
∴∠BOC=70°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=35°,
∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=∠EOF ∠BOE=90° 35°=55°.
21.如图,AB∥EF,∠A=70°,∠C=30°,∠AFC=40°.CD与EF平行吗?请说明理由.
解:CD∥EF,理由如下:
∵AB∥EF,∠A=70°,
∴∠AFE=∠A=70°,
∵∠AFC=40°,
∴∠EFC=∠AFE﹣∠AFC=70°﹣40°=30°,
∵∠C=30°,
∴∠EFC=∠C,
∴CD∥EF.
22.共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利,但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”,随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别
观点
频数(人数)
A
损坏零件
50
B
破译密码
20
C
乱停乱放
a
D
私锁共享单车,归为己用
b
E
其他
30
调查结果扇形图
请根据以上信息,解答下列问题:
(1)填空:a= 60 ;b= 40 ;m= 15 ;
(2)求扇形图中B组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有D组观点的市民人数.
解:(1)50÷25%=200人,c=200×30%=60人,b=200×20%=40人,30÷200=15%,
故答案为:60;40;15;
(2)360°×(1﹣25%﹣30%﹣20%﹣15%)=36°;
答:扇形图中B组所在扇形的圆心角度数为36°.
(3)100×20%=20(万人)
答:持有D组观点的市民人数大约为20万人,
23.已知a+b=7,ab=9.
(1)求a2+b2的值;
(2)如图,若a,b分别是两个正方形的边长,求图中阴影部分的面积.
解:(1)∵a+b=7,ab=9,
∴(a+b)2=a2+b2+2ab=49.
∴a2+b2+18=49.
∴a2+b2=31.
(2)由图知:S阴影=S大正方形﹣S空白=.
∴S阴影====.
24.规定两个非零数a,b之间的一种新运算,如果am=b,那么a※b=m.
例如:因为52=25,所以5※25=2;因为50=1,所以5※1=0.
(1)根据上述规定填空:2※16= 4 ;3※= ﹣3 .
(2)在运算时,按以上规定请说明等式8※9+8※10=8※90成立.
解:(1)∵24=16,
∴2※16=4;
∵,
∴3※=﹣3.
故答案为:4;﹣3;
(2)设8※9=x,8※10=y,则8x=9,8y=10,
8x×8y=8x+y=90,
∴8※90=x+y,
∵8※9+8※10=x+y,
∴8※9+8※10=8※90.
25.周末,小明骑自行车去外婆家,从家出发30分钟后到达甲地,在甲地停车游玩了一段时间后,按原速继续骑行前进,小明离家1小时后,妈妈骑电动车沿小明骑自行车的路线追赶小明,如图是他们离家的路程y(千米)与小明离家时间x(小时)的关系图,已知妈妈骑电动车的速度是小明骑自行车速度的3倍.
(1)小明在甲地游玩时间是
小时;小明骑自行车的速度是
12 千米/小时;妈妈骑电动车的速度是
36 千米/小时;
(2)若妈妈与小明同时到达外婆家,求小明家到外婆家的路程及两人分别骑行的时间.
解:(1)由图象可得,
小明在甲地游玩时间是﹣0.5===(小时),
小明骑自行车的速度是:6÷0.5=12(千米/小时),妈妈骑电动车的速度是12×3=36(千米/小时),
故答案为:,12,36;
(2)设小明家到外婆家的路程为S千米,
+(1﹣),
解得S=12,
∴小明骑行的时间为0.5×2=1(小时),妈妈骑行的时间为=(小时),
答:小明家到外婆家的路程是12千米,小明骑行的时间为1小时,妈妈骑行的时间为小时.
26.如图,已知AB∥CD,点M为平面内一点,AM⊥DM于点M.
(1)如图1,过点M作MG⊥AB于点G,延长GM交CD于N,请说明∠AMG=∠MDC;
(2)如图2,在(1)问的条件下,点E,F分别在GB上,连接ME,MF,DF.已知ME平分∠AMG,MF平分∠GMD,若∠FDM+∠CDF=180°,∠MFD=3∠GME,求∠GME的度数.
解:(1)∵AM⊥MD,
∴∠AMD=90°.
∴∠AMG+∠DMN=180°﹣∠AMD=90°,
∵MG⊥AB,AB∥CD,
∴GN⊥CD,
∴∠MND=90°,
∴∠DMN+∠D=180°﹣∠MND=90°,
∴∠AMG=∠MDC.
(2)∵ME平分∠AMG,MF平分∠GMD,
∴∠GME=∠AME,∠GMF=∠DMF=∠GMD,
设∠GME=x,则∠AME=x,∠MDC=2x,∠MFD=3∠GME=3x,∠GMD=∠AMG+∠AMD=90°+2x,
∴∠GMF=(90°+2x)=45°+x,
∵AB∥CD,
∴∠GFD+∠CDF=180°,
∵∠FDM+∠CDF=180°,
∴∠GFD=∠FDM,
∴2∠GFD+∠CDM=180°,
∴∠GFD=(180°﹣∠CDM)=(180°﹣2x)=90°﹣x,
∴∠MFG=∠GFD﹣∠MFD=90°﹣x﹣3x=90°﹣4x,
在直角三角形GMF中,∠MFG+∠GMF=90°,
∴90o﹣4x+45o+x=90o,
∴x=15o,
∴∠GME=15°.
同课章节目录
