5.1 平行四边形的面积(课件) 数学五年级上册-西师大版(共29张PPT)
文档属性
| 名称 | 5.1 平行四边形的面积(课件) 数学五年级上册-西师大版(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 07:12:06 | ||
图片预览


文档简介
(共29张PPT)
平行四边形的面积
用数方格的方法试一试!
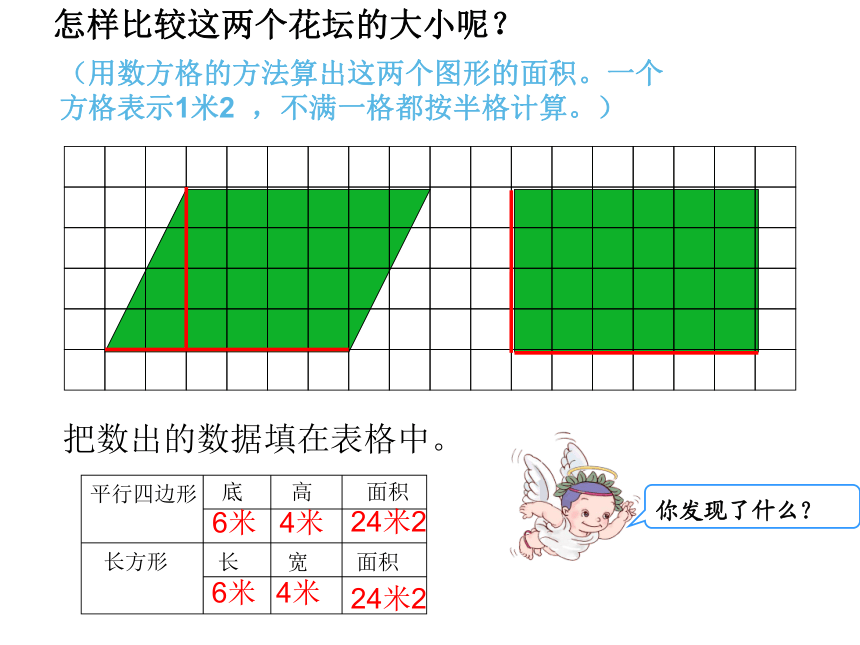
(用数方格的方法算出这两个图形的面积。一个方格表示1米2
,不满一格都按半格计算。)
把数出的数据填在表格中。
平行四边形
长方形
底
高
面积
长
宽
面积
6米
4米
6米
4米
24米2
24米2
怎样比较这两个花坛的大小呢?
你发现了什么?
学习建议
1、请同学们用手中的学具,两人一组,剪一剪、拼一拼、试着把平行四边形拼成长方形。
2、展示不同的方法。
3、观察并思考以下两个问题
A、拼成的长方形和原来的平行四边形比较什么变了?什么没有变?
B、拼成的长方形的长与宽和平行四边形的底和高有什么关系?
演示1
演示2
演示3
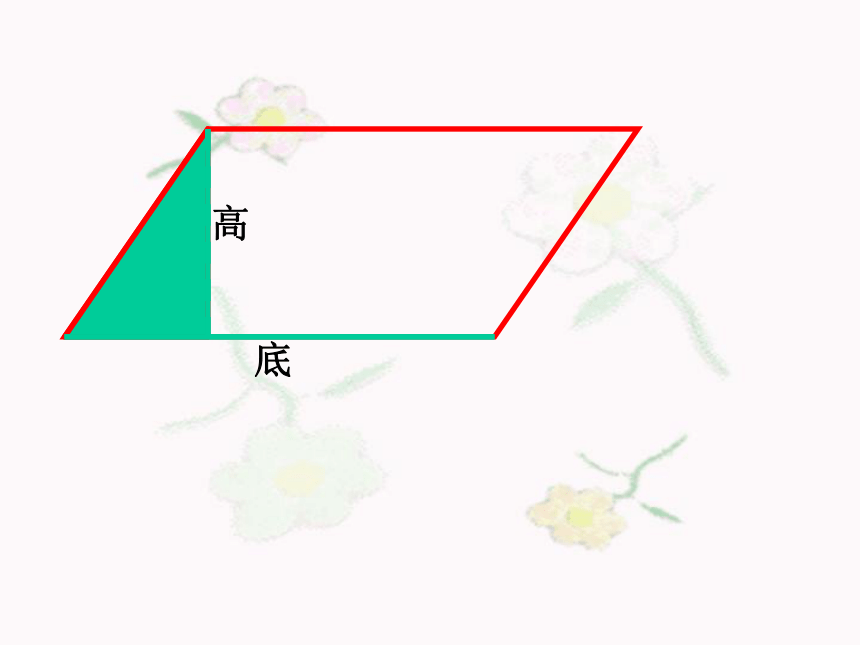
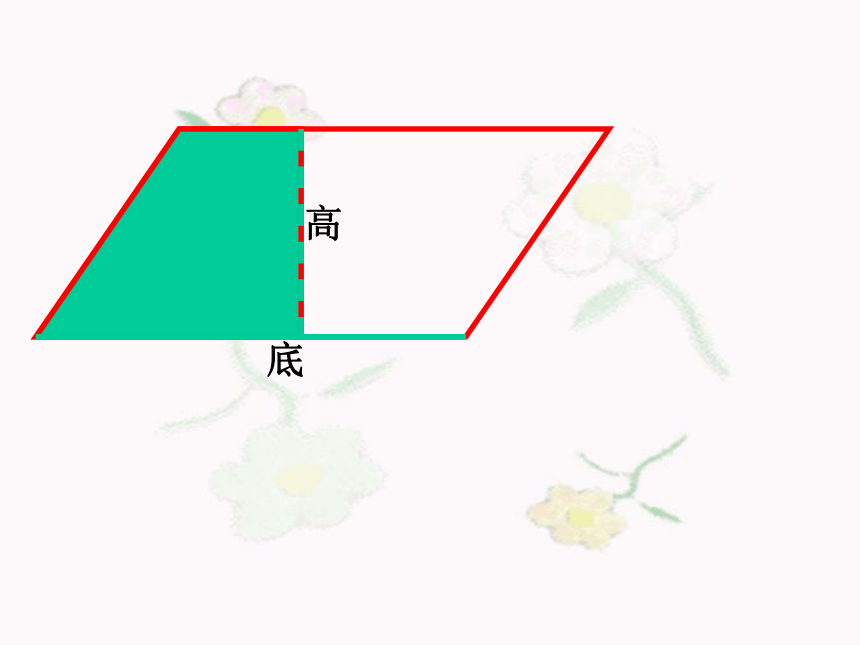
高
底
高
底
高
底
讨论:1、转化成的长方形的面积与原来的
平行四边形的面积比较,有没有变化?为
什么?
2、这个长方形的长与平行四边形的
底有什么关系?
3、这个长方形的宽与平行四边形的
高有什么关系?
长
宽
底
高
平行四边形的面积
长方形的面积
底
长
×
高
=
×
宽
=
S
=
a
×
h
S
=ah
S
=
a
·
h
平行四边形的面积=底×高
平行四边形花坛的底是6m,
S=ah=6×4=24﹝㎡﹞
高是4m,它的面积是多少
6m
4m
S
=ah
=5×2.5
=
12.5(m2)
答:它的面积是
12.5
m2。
判断
(1)
两个平行四边形的高相等,它
们的面积就相等(
)。
(2)
平行四边形高一定,底越长,它
的面积就越大(
)
。
×
√
B
A
返回
A
同
底等高的平行四边形面积相等
(等)
选择:
(1)已知一个平行四边形的底是2米,高是5分米,它的面积是(
)。
A、10平方米
B、100平方分米
C、100分米
(2)已知一个平行四边形的面积是30平方米,底是6米,高是(
)。
A、180平方米
B、5平方米
C、5米
(3)A、B、C中哪一个的面积是3×2=6平方厘米(
)。
2厘米
3厘米
A
3厘米
2厘米
B
2厘米
3厘米
C
课堂小结
回顾我们的学习历程,你最大的发现是什么?
我们用转化的方法推导出了平行四边形的面积公式.
平行四边形(新)
长方形(旧)
转化(割补)
推导
联系
再见
自主感知
1.学生自住交流发现并全班反馈得出
平行四边形的底和长方形的长相等。平行四边形的高和长方形的宽相等。平行四边形的面积和长方形的面积相等。
2提出猜想
平行四边形的面积等于
底×高
学习建议
1、请同学们用手中的学具,剪一剪、拼一拼、试着把平行四边形拼成长方形。
2、展示不同的方法把平行四边形转化成长方形。
3、观察并思考以下两个问题
A、拼成的长方形和原来的平行四边形比较什么变了?什么没有变?
B、拼成的长方形的长与宽和平行四边形的底和高有什么关系?
把平行四边形转化成长方形后,你发现了什么?
1、形状变了,面积没有变。
2、拼成的长方形与平行四边形的底相等,宽与平行四边形的高相等。
3、根据长方形的公式得出平行四边形的面积公式。
4、活动小结:把平行四边形转化成了同它面积相等的长方形,利用长方形的面积公式得出了平行四边形的面积等于
底×高
自主发现
交流反馈
展示结果
平行四边形的面积
用数方格的方法试一试!
(用数方格的方法算出这两个图形的面积。一个方格表示1米2
,不满一格都按半格计算。)
把数出的数据填在表格中。
平行四边形
长方形
底
高
面积
长
宽
面积
6米
4米
6米
4米
24米2
24米2
怎样比较这两个花坛的大小呢?
你发现了什么?
学习建议
1、请同学们用手中的学具,两人一组,剪一剪、拼一拼、试着把平行四边形拼成长方形。
2、展示不同的方法。
3、观察并思考以下两个问题
A、拼成的长方形和原来的平行四边形比较什么变了?什么没有变?
B、拼成的长方形的长与宽和平行四边形的底和高有什么关系?
演示1
演示2
演示3
高
底
高
底
高
底
讨论:1、转化成的长方形的面积与原来的
平行四边形的面积比较,有没有变化?为
什么?
2、这个长方形的长与平行四边形的
底有什么关系?
3、这个长方形的宽与平行四边形的
高有什么关系?
长
宽
底
高
平行四边形的面积
长方形的面积
底
长
×
高
=
×
宽
=
S
=
a
×
h
S
=ah
S
=
a
·
h
平行四边形的面积=底×高
平行四边形花坛的底是6m,
S=ah=6×4=24﹝㎡﹞
高是4m,它的面积是多少
6m
4m
S
=ah
=5×2.5
=
12.5(m2)
答:它的面积是
12.5
m2。
判断
(1)
两个平行四边形的高相等,它
们的面积就相等(
)。
(2)
平行四边形高一定,底越长,它
的面积就越大(
)
。
×
√
B
A
返回
A
同
底等高的平行四边形面积相等
(等)
选择:
(1)已知一个平行四边形的底是2米,高是5分米,它的面积是(
)。
A、10平方米
B、100平方分米
C、100分米
(2)已知一个平行四边形的面积是30平方米,底是6米,高是(
)。
A、180平方米
B、5平方米
C、5米
(3)A、B、C中哪一个的面积是3×2=6平方厘米(
)。
2厘米
3厘米
A
3厘米
2厘米
B
2厘米
3厘米
C
课堂小结
回顾我们的学习历程,你最大的发现是什么?
我们用转化的方法推导出了平行四边形的面积公式.
平行四边形(新)
长方形(旧)
转化(割补)
推导
联系
再见
自主感知
1.学生自住交流发现并全班反馈得出
平行四边形的底和长方形的长相等。平行四边形的高和长方形的宽相等。平行四边形的面积和长方形的面积相等。
2提出猜想
平行四边形的面积等于
底×高
学习建议
1、请同学们用手中的学具,剪一剪、拼一拼、试着把平行四边形拼成长方形。
2、展示不同的方法把平行四边形转化成长方形。
3、观察并思考以下两个问题
A、拼成的长方形和原来的平行四边形比较什么变了?什么没有变?
B、拼成的长方形的长与宽和平行四边形的底和高有什么关系?
把平行四边形转化成长方形后,你发现了什么?
1、形状变了,面积没有变。
2、拼成的长方形与平行四边形的底相等,宽与平行四边形的高相等。
3、根据长方形的公式得出平行四边形的面积公式。
4、活动小结:把平行四边形转化成了同它面积相等的长方形,利用长方形的面积公式得出了平行四边形的面积等于
底×高
自主发现
交流反馈
展示结果
