2021-2022学年冀教版九年级上册数学《第28章 圆》单元测试(word解析版)
文档属性
| 名称 | 2021-2022学年冀教版九年级上册数学《第28章 圆》单元测试(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 239.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-02 16:05:25 | ||
图片预览



文档简介
2021-2022学年冀教新版九年级上册数学
《第28章
圆》单元测试卷
一.选择题
1.下列命题为真命题的是( )
A.平面内任意三点确定一个圆
B.五边形的内角和为540°
C.如果a>b,则ac2>bc2
D.如果两条直线被第三条直线所截,那么所截得的同位角相等
2.对圆的周长公式的说法正确的是( )
A.r是变量,2是常量
B.C,r是变量,2是常量
C.r是变量,2,C是常量
D.C是变量,2,r是常量
3.如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )
A.65°
B.60°
C.55°
D.50°
4.下列说法:①直径是弦;②长度相等的两条弧是等弧;③任何一条直径所在的直线都是圆的对称轴;④任何一条直径都是圆的对称轴,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
5.下列关于圆的说法,正确的是( )
A.弦是直径,直径也是弦
B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴
D.过三点可以作一个圆
6.直角三角形两直角边长分别为和1,那么它的外接圆的直径是( )
A.1
B.2
C.3
D.4
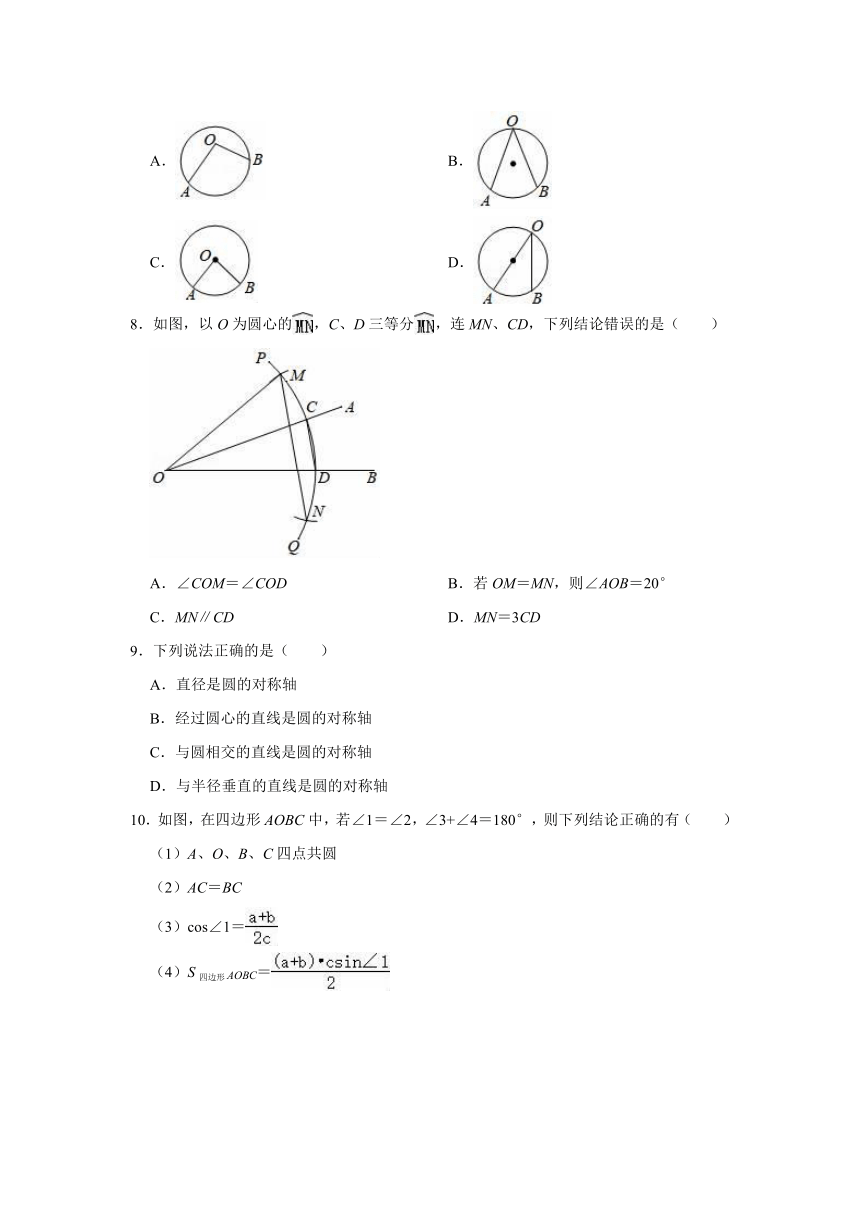
7.下列图形中,∠AOB为圆心角的是( )
A.
B.
C.
D.
8.如图,以O为圆心的,C、D三等分,连MN、CD,下列结论错误的是( )
A.∠COM=∠COD
B.若OM=MN,则∠AOB=20°
C.MN∥CD
D.MN=3CD
9.下列说法正确的是( )
A.直径是圆的对称轴
B.经过圆心的直线是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与半径垂直的直线是圆的对称轴
10.如图,在四边形AOBC中,若∠1=∠2,∠3+∠4=180°,则下列结论正确的有( )
(1)A、O、B、C四点共圆
(2)AC=BC
(3)cos∠1=
(4)S四边形AOBC=
A.1个
B.2个
C.3个
D.4个
二.填空题
11.“三点定圆”的含义是:
的三点确定一个圆.
12.如图是央行发布的建国70周年纪念银币的背面图案,这枚纪念币的周长是21.98厘米,它的直径是
厘米,面积是
平方厘米(π取3.14).
13.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都
,这个距离就是这个圆的
.
14.确定一个圆的两个条件是
和
,
决定圆的位置,
决定圆的大小.
15.设方程x2﹣17x+60=0的两根为Rt△ABC的两条直角边的长,则Rt△ABC外接圆的半径是
.
16.如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE=
.
17.如图,点C,D在半圆的直径AB上,且CO=OD,点E在上,△ECD为以DE为斜边的等腰直角三角形.若半圆的半径为,则DE的长为
.
18.如图,已知AB是⊙O的直径,AB=20,弦CD与AB相交于点E,∠AEC=30°,,则的值为
.
19.如图,在△ABC中,AC=3,BC=4,AB=5,∠CAB的平分线交于点D,则AD的长是
.
20.如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:
①∠MAD=∠AND;
②CP=a﹣;
③△ABM≌△NGF;
④S四边形AMFN=a2+b2;
⑤A,M,P,D四点共圆,其中正确的序号为
.
三.解答题
21.已知线段AB=4cm,以3cm长为半径作圆,使它经过点A、B,能作几个这样的?请作出符合要求的图.
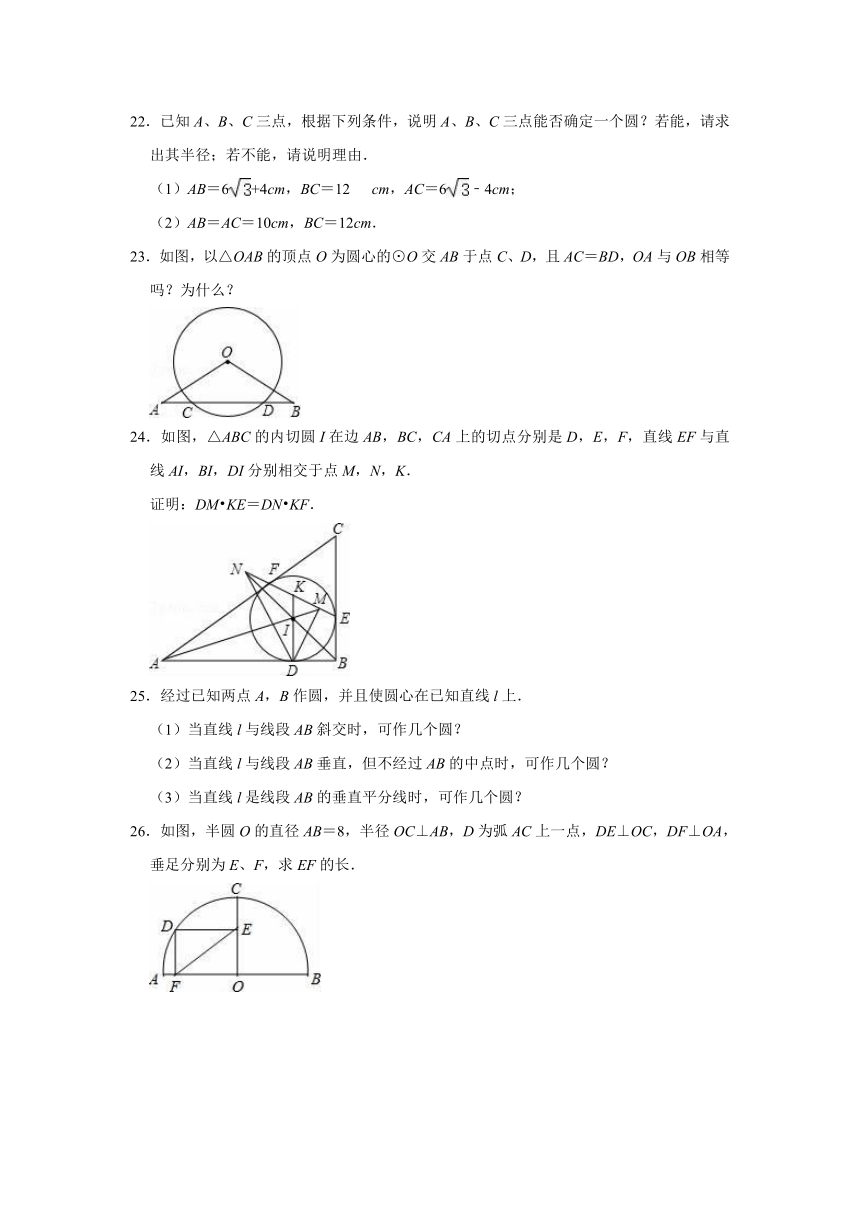
22.已知A、B、C三点,根据下列条件,说明A、B、C三点能否确定一个圆?若能,请求出其半径;若不能,请说明理由.
(1)AB=6+4cm,BC=12cm,AC=6﹣4cm;
(2)AB=AC=10cm,BC=12cm.
23.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD,OA与OB相等吗?为什么?
24.如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.
证明:DM KE=DN KF.
25.经过已知两点A,B作圆,并且使圆心在已知直线l上.
(1)当直线l与线段AB斜交时,可作几个圆?
(2)当直线l与线段AB垂直,但不经过AB的中点时,可作几个圆?
(3)当直线l是线段AB的垂直平分线时,可作几个圆?
26.如图,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E、F,求EF的长.
参考答案与试题解析
一.选择题
1.解:A、平面内不在同一直线上的三点确定一个圆,故本选项错误;
B、五边形的内角和为(5﹣2)×180°=540°,故本选项正确;
C、当c=0时,原式不成立,故本选项错误;
D、两直线平行,同位角相等,故本选项错误.
故选:B.
2.解:圆的周长公式为C=2πr,
变量是C、r,常量是2、π,B正确;
故选:B.
3.解:∵OB=OC,
∴∠OCB=∠OBC=40°,
∴∠BOC=180°﹣40°﹣40°=100°,
由圆周角定理得,∠A=∠BOC=50°,
故选:D.
4.解:①直径是最长的弦,故本小题正确;
②在等圆或同圆中,长度相等的两条弧是等弧,故本小题错误;
③经过圆心的每一条直线都是圆的对称轴,故本小题正确;
④经过圆心的每一条直线都是圆的对称轴,故本小题错误.
故选:B.
5.解:A、弦不一定是直径,但直径是弦,本选项说法错误,不符合题意;
B、∵半圆小于优弧,
∴半圆是圆中最长的弧说法错误,本选项不符合题意;
C、圆的每一条直径所在的直线都是它的对称轴,本选项说法正确,符合题意;
D、过不在同一直线上的三点可以作一个圆,本选项说法错误,不符合题意;
故选:C.
6.解:由勾股定理得,直角三角形的斜边长==2,
∴它的外接圆的直径是2,
故选:B.
7.解:根据圆心角定义可知:
A.顶点不是圆心,所以A选项不符合题意;
B.顶点在圆上,∠AOB圆周角,所以B选项不符合题意;
C.∠AOB顶点是圆心,两边与圆相交,所以C选项符合题意;
D.顶点在圆上,∠AOB圆周角,所以D选项不符合题意.
故选:C.
8.解:连接ON、MC、DN,过点O作OE⊥CD交于点E,
∵=,
∴∠COM=∠COD,A选项结论正确,不符合题意;
∵OM=MN,OM=ON,
∴OM=ON=MN,
∴△OMN为等边三角形,
∴∠MON=60°,
∵==,
∴∠AOB=20°,B选项结论正确,不符合题意;
∵OE⊥CD,
∴=,
∴=,
∴OE⊥MN,
∴MN∥CD,C选项结论正确,不符合题意;
∵MC+CD+DN>MN,
∴MN<3CD,D选项结论错误,符合题意;
故选:D.
9.解:A、直径所在的直线为圆的对称轴,所以A错误;
B、经过圆心的直线是圆的对称轴,所以B正确;
C、与圆相交的直线不一定是圆的对称轴,所以C错误;
D、与半径垂直的直线不一定是圆的对称轴,所以D错误.
故选:B.
10.解:∵∠3+∠4=180°,
∴A、O、B、C四点共圆,(1)正确;
作CD⊥OA于D,CE⊥OB于E,如图所示:
则∠CDA=∠CEB=90°,
∵∠1=∠2,
∴CD=CE,
∵∠3+∠4=180°,∠3+∠CAD=180°,
∴∠CAD=∠4,
在△ACD和△BCE中,,
∴△ACD≌△BCE(AAS),
∴AD=BE,AC=BC,(2)正确;
∵cos∠1==,cos∠2==,
∴cos∠1+cos∠2=+==,
∵∠1=∠2,
∴cos∠1=cos∠2,
∴2cos∠1=,
∴cos∠1=,(3)正确;
∵CD=CE,sin∠1=,
∴CD=c×sin∠1,
∴S四边形AOBC=S△OAC+S△BOC=a×CD+b×CE=(a+b)CD=(a+b)×c×sin∠1=,(4)正确;
正确的结论有4个,
故选:D.
二.填空题
11.解:“三点定圆”的含义是:不在同一直线上的三点确定一个圆.
故答案为:不在同一直线上.
12.解:由题意得,直径=21.98÷3.14=7,面积=π×=π;
故答案为:7,π.
13.解:参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都相等,这个距离就是这个圆的半径.
故答案为:相等,半径.
14.解:确定一个圆的两个条件是圆心和半径,圆心决定圆的位置,半径决定圆的大小,
故答案为:圆心,半径,圆心,半径.
15.解:解方程x2﹣17x+60=0,得x1=5,x2=12,
则Rt△ABC的两条直角边的长为5和12,
由勾股定理得,Rt△ABC的斜边长==13,
∴Rt△ABC外接圆的半径为,
故答案为:.
16.解:连接OC,作EF⊥OC于F,
∵点A关于直线CD的对称点为E,点E落在半径OA上,
∴CE=CA,
∵=,
∴∠AOC=∠AOB=30°,
∵OA=OC,
∴∠OAC=∠OCA=75°,
∵CE=CA,
∴∠CAE=∠CEA=75°,
∴∠CAE=30°,
∴∠ECF=45°,
设EF=x,则FC=x,
在Rt△EOF中,tan∠EOF=,
∴OF==x,
由题意得,OF+FC=OC,即x+x=4,
解得,x=2﹣2,
∵∠EOF=30°,
∴OE=2EF=4﹣4,
故答案为:4﹣4.
17.解:连接OE,
设CE长为a,则OC=a,CD=a,
在Rt△ECO中,a2+(a)2=()2,
解得a=±2(负值舍去),
在Rt△ECD中,DE==2.
故答案为:2.
18.解:过点O作OF⊥CD于F,连接DO,
∵AB=20,
∴AO=OB=OD=10,
∵OE:AE=2:3,
∴OE=4.AE=6,
∵∠AEC=30°,
∴∠OEF=30°,
∴OF=OE=2;
∴DF==4,
由垂径定理得:CD=2DF=8,
∴==.
19.解:设△ABC的外接圆的圆心为O,连接OD,过D作DE⊥AB于E,如图所示:
∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴AB为半圆O的直径,
∴OD=OA=AB=,
∵AD平分∠CAB,
∴,
∴∠DOE=∠BAC,
∴sin∠DOE=sin∠BAC,
∴=,
即=,
解得:DE=2,
∴OE===,
∴AE=OA+OE=4,
∴AD===2,
故答案为:2.
20.解:①∵四边形ABCD是正方形,
∴∠BAD=∠ADC=∠B=90°,
∴∠BAM+∠DAM=90°,
∵将△ABM绕点A旋转至△ADN,
∴∠NAD=∠BAM,∠AND=∠AMB,
∴∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,
∴∠DAM=∠AND,故①正确;
②∵四边形CEFG是正方形,
∴PC∥EF,
∴△MPC∽△MFE,
∴=,
∵大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),BM=b,
∴EF=b,CM=a﹣b,ME=(a﹣b)+b=a,
∴=,
∴CP=b﹣;故②错误;
③∵将△MEF绕点F旋转至△NGF,
∴GN=ME,
∵AB=a,ME=a,
∴AB=ME=NG,
在△ABM与△NGF中,,
∴△ABM≌△NGF(SAS);故③正确;
④∵将△ABM绕点A旋转至△ADN,
∴AM=AN,
∵将△MEF绕点F旋转至△NGF,
∴NF=MF,
∵△ABM≌△NGF,
∴AM=NF,
∴四边形AMFN是矩形,
∵∠BAM=∠NAD,
∴∠BAM+DAM=∠NAD+∠DAN=90°,
∴∠NAM=90°,
∴四边形AMFN是正方形,
在Rt△ABM中,a2+b2=AM2,
∴S四边形AMFN=AM2=a2+b2;故④正确;
⑤∵四边形AMFN是正方形,
∴∠AMP=90°,
∵∠ADP=90°,
∴∠AMP+∠ADP=180°,
∴A,M,P,D四点共圆,故⑤正确.
故答案为:①③④⑤.
三.解答题
21.解:这样的圆能画2个.如图:
作AB的垂直平分线l,再以点A为圆心,3cm为半径作圆交l于O1和O2,然后分别以O1和O2为圆心,以3cm为半径作圆,
则⊙O1和⊙O2为所求圆.
22.解:(1)∵6+4+6﹣4=12,
∴AB+AC=BC,
∴A、B、C三点共线,
∴不能确定一个圆;
(2)∵10+10=20>12,
∴A、B、C三点不共线,
∴能确定一个圆;
过A作AD⊥BC,连接BO,
∵BC=12,
∴DB=6,
∵AB=10,
∴AD==8,
设OB=x,则DO=8﹣x,
x2﹣62=(8﹣x)2,
解得:x=.
∴A、B、C三点能确定一个圆,半径为.
23.答:OA=OB.
理由如下:
如图,过O作OE⊥AB于E,
∵CD是⊙O的弦,OE⊥CD,
∴CE=DE,
∵AC=BD,
∴AE=BE,
∵OE⊥CD,
∴OA=OB.
24.证明:连接IE,如图所示:
∵△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,
∴ID⊥AB,IE⊥BC,
∴∠IDB=∠IEB=90°,
∴∠IDB+∠IEB=180°,
∴I,D,B,E四点共圆.
又∵∠AID=90°﹣∠IAD,∠MED=∠FDA=90°﹣∠IAD,
∴∠AID=∠MED,
∴I,D,E,M四点共圆.
∴I,D,B,E,M五点共圆,∠IMB=∠IEB=90°,
即AM⊥BM.
同理,I,D,A,N,F五点共圆,且BN⊥AN.
设直线AN,BM交于点G,则点I为△GAB的垂心.又ID⊥AB,
∴G,I,D共线.
∵G,N,D,B四点共圆,
∴∠ADN=∠G.
同理∠BDM=∠G.
∴DK平分∠MDN,
∴①.
又由I,D,E,M;I,D,N,F分别共圆,
∴KM KE=KI KD=KF KN,
∴②.
由①,②得:,
∴DM KE=DN KF.
25.解:(1)当直线l与线段AB斜交时,直线l与线段AB的垂直平分线只有一个交点,
∴可作1个圆;
(2)当直线l与线段AB垂直,但不经过AB的中点时,直线l与线段AB的垂直平分线没有交点,
∴可作0个圆;
(3)当直线l是线段AB的垂直平分线时,可作无数个圆.
26.解:连接OD.
∵OC⊥AB
DE⊥OC,DF⊥OA,
∴∠AOC=∠DEO=∠DFO=90°,
∴四边形DEOF是矩形,
∴EF=OD.
∵OD=OA
∴EF=OA=4.
《第28章
圆》单元测试卷
一.选择题
1.下列命题为真命题的是( )
A.平面内任意三点确定一个圆
B.五边形的内角和为540°
C.如果a>b,则ac2>bc2
D.如果两条直线被第三条直线所截,那么所截得的同位角相等
2.对圆的周长公式的说法正确的是( )
A.r是变量,2是常量
B.C,r是变量,2是常量
C.r是变量,2,C是常量
D.C是变量,2,r是常量
3.如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )
A.65°
B.60°
C.55°
D.50°
4.下列说法:①直径是弦;②长度相等的两条弧是等弧;③任何一条直径所在的直线都是圆的对称轴;④任何一条直径都是圆的对称轴,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
5.下列关于圆的说法,正确的是( )
A.弦是直径,直径也是弦
B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴
D.过三点可以作一个圆
6.直角三角形两直角边长分别为和1,那么它的外接圆的直径是( )
A.1
B.2
C.3
D.4
7.下列图形中,∠AOB为圆心角的是( )
A.
B.
C.
D.
8.如图,以O为圆心的,C、D三等分,连MN、CD,下列结论错误的是( )
A.∠COM=∠COD
B.若OM=MN,则∠AOB=20°
C.MN∥CD
D.MN=3CD
9.下列说法正确的是( )
A.直径是圆的对称轴
B.经过圆心的直线是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与半径垂直的直线是圆的对称轴
10.如图,在四边形AOBC中,若∠1=∠2,∠3+∠4=180°,则下列结论正确的有( )
(1)A、O、B、C四点共圆
(2)AC=BC
(3)cos∠1=
(4)S四边形AOBC=
A.1个
B.2个
C.3个
D.4个
二.填空题
11.“三点定圆”的含义是:
的三点确定一个圆.
12.如图是央行发布的建国70周年纪念银币的背面图案,这枚纪念币的周长是21.98厘米,它的直径是
厘米,面积是
平方厘米(π取3.14).
13.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都
,这个距离就是这个圆的
.
14.确定一个圆的两个条件是
和
,
决定圆的位置,
决定圆的大小.
15.设方程x2﹣17x+60=0的两根为Rt△ABC的两条直角边的长,则Rt△ABC外接圆的半径是
.
16.如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE=
.
17.如图,点C,D在半圆的直径AB上,且CO=OD,点E在上,△ECD为以DE为斜边的等腰直角三角形.若半圆的半径为,则DE的长为
.
18.如图,已知AB是⊙O的直径,AB=20,弦CD与AB相交于点E,∠AEC=30°,,则的值为
.
19.如图,在△ABC中,AC=3,BC=4,AB=5,∠CAB的平分线交于点D,则AD的长是
.
20.如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:
①∠MAD=∠AND;
②CP=a﹣;
③△ABM≌△NGF;
④S四边形AMFN=a2+b2;
⑤A,M,P,D四点共圆,其中正确的序号为
.
三.解答题
21.已知线段AB=4cm,以3cm长为半径作圆,使它经过点A、B,能作几个这样的?请作出符合要求的图.
22.已知A、B、C三点,根据下列条件,说明A、B、C三点能否确定一个圆?若能,请求出其半径;若不能,请说明理由.
(1)AB=6+4cm,BC=12cm,AC=6﹣4cm;
(2)AB=AC=10cm,BC=12cm.
23.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD,OA与OB相等吗?为什么?
24.如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.
证明:DM KE=DN KF.
25.经过已知两点A,B作圆,并且使圆心在已知直线l上.
(1)当直线l与线段AB斜交时,可作几个圆?
(2)当直线l与线段AB垂直,但不经过AB的中点时,可作几个圆?
(3)当直线l是线段AB的垂直平分线时,可作几个圆?
26.如图,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E、F,求EF的长.
参考答案与试题解析
一.选择题
1.解:A、平面内不在同一直线上的三点确定一个圆,故本选项错误;
B、五边形的内角和为(5﹣2)×180°=540°,故本选项正确;
C、当c=0时,原式不成立,故本选项错误;
D、两直线平行,同位角相等,故本选项错误.
故选:B.
2.解:圆的周长公式为C=2πr,
变量是C、r,常量是2、π,B正确;
故选:B.
3.解:∵OB=OC,
∴∠OCB=∠OBC=40°,
∴∠BOC=180°﹣40°﹣40°=100°,
由圆周角定理得,∠A=∠BOC=50°,
故选:D.
4.解:①直径是最长的弦,故本小题正确;
②在等圆或同圆中,长度相等的两条弧是等弧,故本小题错误;
③经过圆心的每一条直线都是圆的对称轴,故本小题正确;
④经过圆心的每一条直线都是圆的对称轴,故本小题错误.
故选:B.
5.解:A、弦不一定是直径,但直径是弦,本选项说法错误,不符合题意;
B、∵半圆小于优弧,
∴半圆是圆中最长的弧说法错误,本选项不符合题意;
C、圆的每一条直径所在的直线都是它的对称轴,本选项说法正确,符合题意;
D、过不在同一直线上的三点可以作一个圆,本选项说法错误,不符合题意;
故选:C.
6.解:由勾股定理得,直角三角形的斜边长==2,
∴它的外接圆的直径是2,
故选:B.
7.解:根据圆心角定义可知:
A.顶点不是圆心,所以A选项不符合题意;
B.顶点在圆上,∠AOB圆周角,所以B选项不符合题意;
C.∠AOB顶点是圆心,两边与圆相交,所以C选项符合题意;
D.顶点在圆上,∠AOB圆周角,所以D选项不符合题意.
故选:C.
8.解:连接ON、MC、DN,过点O作OE⊥CD交于点E,
∵=,
∴∠COM=∠COD,A选项结论正确,不符合题意;
∵OM=MN,OM=ON,
∴OM=ON=MN,
∴△OMN为等边三角形,
∴∠MON=60°,
∵==,
∴∠AOB=20°,B选项结论正确,不符合题意;
∵OE⊥CD,
∴=,
∴=,
∴OE⊥MN,
∴MN∥CD,C选项结论正确,不符合题意;
∵MC+CD+DN>MN,
∴MN<3CD,D选项结论错误,符合题意;
故选:D.
9.解:A、直径所在的直线为圆的对称轴,所以A错误;
B、经过圆心的直线是圆的对称轴,所以B正确;
C、与圆相交的直线不一定是圆的对称轴,所以C错误;
D、与半径垂直的直线不一定是圆的对称轴,所以D错误.
故选:B.
10.解:∵∠3+∠4=180°,
∴A、O、B、C四点共圆,(1)正确;
作CD⊥OA于D,CE⊥OB于E,如图所示:
则∠CDA=∠CEB=90°,
∵∠1=∠2,
∴CD=CE,
∵∠3+∠4=180°,∠3+∠CAD=180°,
∴∠CAD=∠4,
在△ACD和△BCE中,,
∴△ACD≌△BCE(AAS),
∴AD=BE,AC=BC,(2)正确;
∵cos∠1==,cos∠2==,
∴cos∠1+cos∠2=+==,
∵∠1=∠2,
∴cos∠1=cos∠2,
∴2cos∠1=,
∴cos∠1=,(3)正确;
∵CD=CE,sin∠1=,
∴CD=c×sin∠1,
∴S四边形AOBC=S△OAC+S△BOC=a×CD+b×CE=(a+b)CD=(a+b)×c×sin∠1=,(4)正确;
正确的结论有4个,
故选:D.
二.填空题
11.解:“三点定圆”的含义是:不在同一直线上的三点确定一个圆.
故答案为:不在同一直线上.
12.解:由题意得,直径=21.98÷3.14=7,面积=π×=π;
故答案为:7,π.
13.解:参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都相等,这个距离就是这个圆的半径.
故答案为:相等,半径.
14.解:确定一个圆的两个条件是圆心和半径,圆心决定圆的位置,半径决定圆的大小,
故答案为:圆心,半径,圆心,半径.
15.解:解方程x2﹣17x+60=0,得x1=5,x2=12,
则Rt△ABC的两条直角边的长为5和12,
由勾股定理得,Rt△ABC的斜边长==13,
∴Rt△ABC外接圆的半径为,
故答案为:.
16.解:连接OC,作EF⊥OC于F,
∵点A关于直线CD的对称点为E,点E落在半径OA上,
∴CE=CA,
∵=,
∴∠AOC=∠AOB=30°,
∵OA=OC,
∴∠OAC=∠OCA=75°,
∵CE=CA,
∴∠CAE=∠CEA=75°,
∴∠CAE=30°,
∴∠ECF=45°,
设EF=x,则FC=x,
在Rt△EOF中,tan∠EOF=,
∴OF==x,
由题意得,OF+FC=OC,即x+x=4,
解得,x=2﹣2,
∵∠EOF=30°,
∴OE=2EF=4﹣4,
故答案为:4﹣4.
17.解:连接OE,
设CE长为a,则OC=a,CD=a,
在Rt△ECO中,a2+(a)2=()2,
解得a=±2(负值舍去),
在Rt△ECD中,DE==2.
故答案为:2.
18.解:过点O作OF⊥CD于F,连接DO,
∵AB=20,
∴AO=OB=OD=10,
∵OE:AE=2:3,
∴OE=4.AE=6,
∵∠AEC=30°,
∴∠OEF=30°,
∴OF=OE=2;
∴DF==4,
由垂径定理得:CD=2DF=8,
∴==.
19.解:设△ABC的外接圆的圆心为O,连接OD,过D作DE⊥AB于E,如图所示:
∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴AB为半圆O的直径,
∴OD=OA=AB=,
∵AD平分∠CAB,
∴,
∴∠DOE=∠BAC,
∴sin∠DOE=sin∠BAC,
∴=,
即=,
解得:DE=2,
∴OE===,
∴AE=OA+OE=4,
∴AD===2,
故答案为:2.
20.解:①∵四边形ABCD是正方形,
∴∠BAD=∠ADC=∠B=90°,
∴∠BAM+∠DAM=90°,
∵将△ABM绕点A旋转至△ADN,
∴∠NAD=∠BAM,∠AND=∠AMB,
∴∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,
∴∠DAM=∠AND,故①正确;
②∵四边形CEFG是正方形,
∴PC∥EF,
∴△MPC∽△MFE,
∴=,
∵大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),BM=b,
∴EF=b,CM=a﹣b,ME=(a﹣b)+b=a,
∴=,
∴CP=b﹣;故②错误;
③∵将△MEF绕点F旋转至△NGF,
∴GN=ME,
∵AB=a,ME=a,
∴AB=ME=NG,
在△ABM与△NGF中,,
∴△ABM≌△NGF(SAS);故③正确;
④∵将△ABM绕点A旋转至△ADN,
∴AM=AN,
∵将△MEF绕点F旋转至△NGF,
∴NF=MF,
∵△ABM≌△NGF,
∴AM=NF,
∴四边形AMFN是矩形,
∵∠BAM=∠NAD,
∴∠BAM+DAM=∠NAD+∠DAN=90°,
∴∠NAM=90°,
∴四边形AMFN是正方形,
在Rt△ABM中,a2+b2=AM2,
∴S四边形AMFN=AM2=a2+b2;故④正确;
⑤∵四边形AMFN是正方形,
∴∠AMP=90°,
∵∠ADP=90°,
∴∠AMP+∠ADP=180°,
∴A,M,P,D四点共圆,故⑤正确.
故答案为:①③④⑤.
三.解答题
21.解:这样的圆能画2个.如图:
作AB的垂直平分线l,再以点A为圆心,3cm为半径作圆交l于O1和O2,然后分别以O1和O2为圆心,以3cm为半径作圆,
则⊙O1和⊙O2为所求圆.
22.解:(1)∵6+4+6﹣4=12,
∴AB+AC=BC,
∴A、B、C三点共线,
∴不能确定一个圆;
(2)∵10+10=20>12,
∴A、B、C三点不共线,
∴能确定一个圆;
过A作AD⊥BC,连接BO,
∵BC=12,
∴DB=6,
∵AB=10,
∴AD==8,
设OB=x,则DO=8﹣x,
x2﹣62=(8﹣x)2,
解得:x=.
∴A、B、C三点能确定一个圆,半径为.
23.答:OA=OB.
理由如下:
如图,过O作OE⊥AB于E,
∵CD是⊙O的弦,OE⊥CD,
∴CE=DE,
∵AC=BD,
∴AE=BE,
∵OE⊥CD,
∴OA=OB.
24.证明:连接IE,如图所示:
∵△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,
∴ID⊥AB,IE⊥BC,
∴∠IDB=∠IEB=90°,
∴∠IDB+∠IEB=180°,
∴I,D,B,E四点共圆.
又∵∠AID=90°﹣∠IAD,∠MED=∠FDA=90°﹣∠IAD,
∴∠AID=∠MED,
∴I,D,E,M四点共圆.
∴I,D,B,E,M五点共圆,∠IMB=∠IEB=90°,
即AM⊥BM.
同理,I,D,A,N,F五点共圆,且BN⊥AN.
设直线AN,BM交于点G,则点I为△GAB的垂心.又ID⊥AB,
∴G,I,D共线.
∵G,N,D,B四点共圆,
∴∠ADN=∠G.
同理∠BDM=∠G.
∴DK平分∠MDN,
∴①.
又由I,D,E,M;I,D,N,F分别共圆,
∴KM KE=KI KD=KF KN,
∴②.
由①,②得:,
∴DM KE=DN KF.
25.解:(1)当直线l与线段AB斜交时,直线l与线段AB的垂直平分线只有一个交点,
∴可作1个圆;
(2)当直线l与线段AB垂直,但不经过AB的中点时,直线l与线段AB的垂直平分线没有交点,
∴可作0个圆;
(3)当直线l是线段AB的垂直平分线时,可作无数个圆.
26.解:连接OD.
∵OC⊥AB
DE⊥OC,DF⊥OA,
∴∠AOC=∠DEO=∠DFO=90°,
∴四边形DEOF是矩形,
∴EF=OD.
∵OD=OA
∴EF=OA=4.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
