2021-2022学年人教版八年级数学上册13.1.2 线段的垂直平分线的性质课件(15张ppt)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.1.2 线段的垂直平分线的性质课件(15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 192.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-02 16:53:47 | ||
图片预览


文档简介
(共15张PPT)
第1课时
线段的垂直平分线的性质与判定
13.1.2
线段的垂直平分线的性质
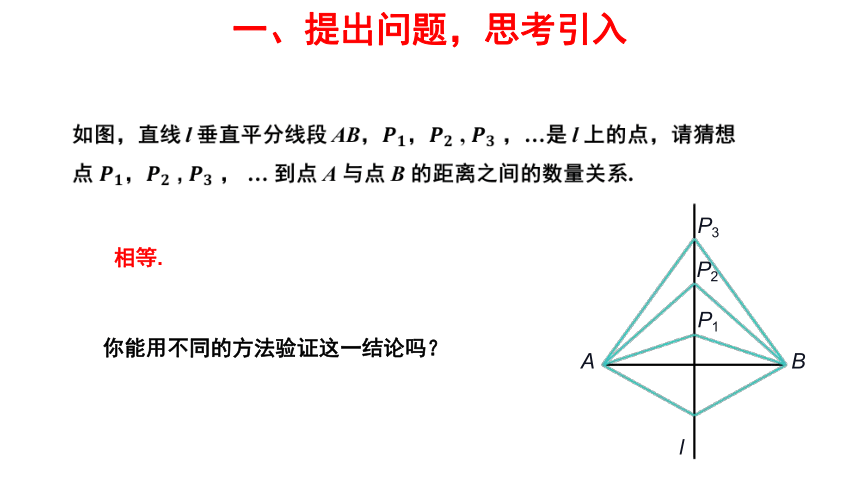
A
B
l
P1
P2
P3
相等.
你能用不同的方法验证这一结论吗?
一、提出问题,思考引入
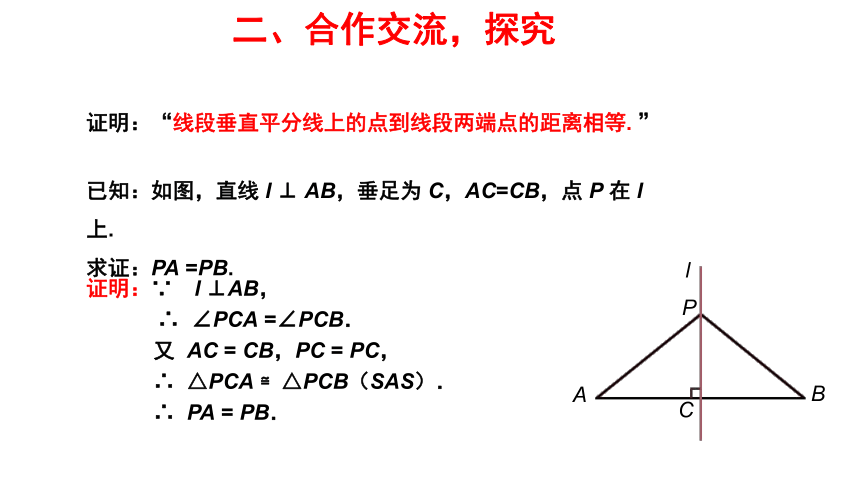
证明:“线段垂直平分线上的点到线段两端点的距离相等.
”
已知:如图,直线
l
⊥
AB,垂足为
C,AC=CB,点
P
在
l
上.
求证:PA
=PB.
证明:∵ l
⊥AB,
∴
∠PCA
=∠PCB.
又
AC
=
CB,PC
=
PC,
∴
△PCA
≌△PCB(SAS).
∴
PA
=
PB.
A
B
P
C
l
二、合作交流,探究新知
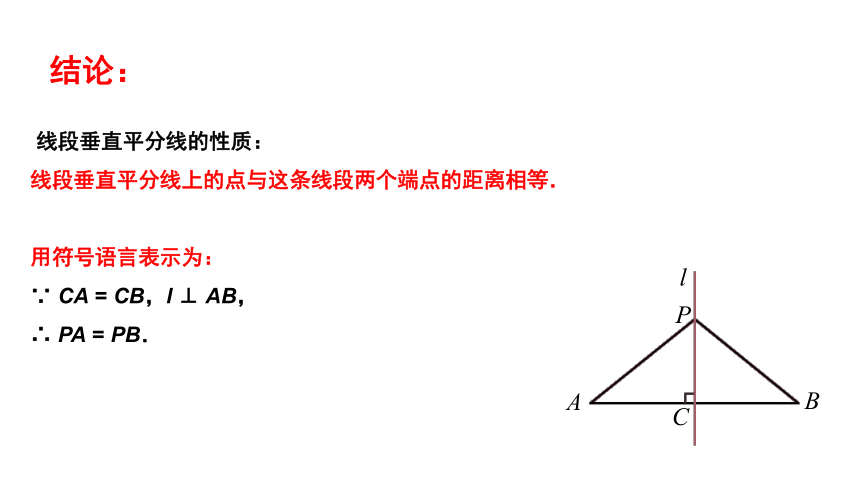
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
用符号语言表示为:
∵
CA
=
CB,l
⊥
AB,
∴
PA
=
PB.
结论:
A
B
P
C
l
反过来,如果
PA
=
PB,那么点
P
是否在线段
AB
的
垂直平分线上呢?
点
P
在线段
AB
的垂直平分线上.
P
A
B
C
二、合作交流,探究新知
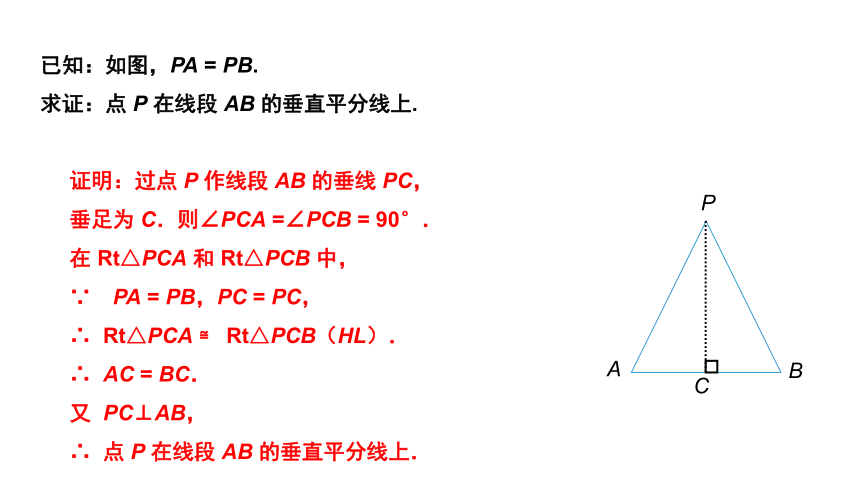
已知:如图,PA
=
PB.
求证:点
P
在线段
AB
的垂直平分线上.
证明:过点
P
作线段
AB
的垂线
PC,
垂足为
C.则∠PCA
=∠PCB
=
90°.
在
Rt△PCA
和
Rt△PCB
中,
∵ PA
=
PB,PC
=
PC,
∴
Rt△PCA
≌
Rt△PCB(HL).
∴
AC
=
BC.
又
PC⊥AB,
∴
点
P
在线段
AB
的垂直平分线上.
P
A
B
C
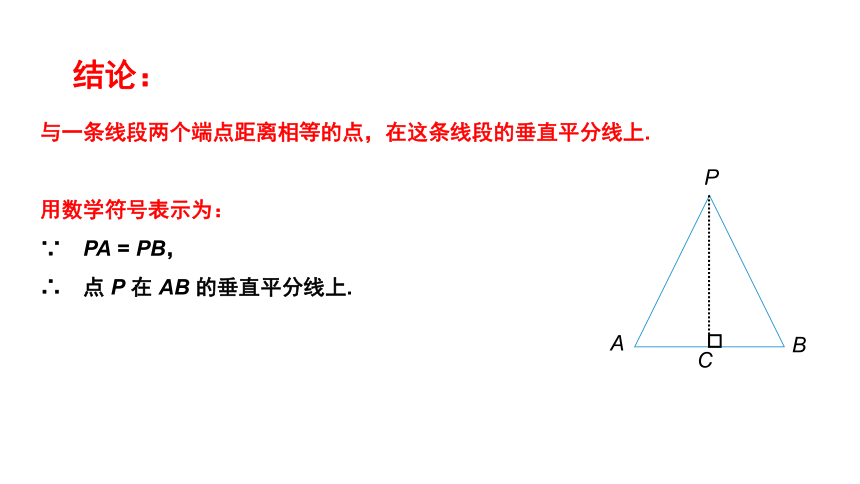
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
用数学符号表示为:
∵ PA
=
PB,
∴ 点
P
在
AB
的垂直平分线上.
结论:
P
A
B
C
你能再找一些到线段
AB
两端点的距离相等的点吗?能找到多少个到线段
AB
两端点距离相等的点?这些点能组成什么几何图形?
在线段
AB
的垂直平分线
l
上的点与
A,B
的距离都相等;反过来,与
A,B
的距离相等的点都在直线
l上,所以直线l
可以看成与两点
A、B
的距离相等的所有点的集合.
P
A
B
C
二、合作交流,探究新知
尺规作图:
如何用尺规作图的方法经过直线外一点作已知直线的垂线?
C
A
B
D
K
F
E
大家拿出圆规和直尺,按照教材中的作法一起来做一做.
三、运用新知
我们已能用尺规完成:
那么利用尺规还能解决什么作图问题呢?
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
(4)经过已知直线外一点作这条直线的垂线.
三、运用新知
例1 如图,AB=AC=8
cm,AB的垂直平分线交AC于点D.若△ADB的周长为18
cm,求DC的长.
讲
校
坛
解:∵DM是AB的垂直平分线,
∴AD=BD.
设CD的长为x,则AD=AC-CD=8-x.
∵C△ADB=AB+AD+BD=8+(8-x)+(8-x)=18,
∴x=3,即CD的长为3
cm.
【点拨】 由线段垂直平分线的性质得AD=BD进而求解.
三、运用新知
训
固
四、巩固新知
1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为(
B
)
A.6
B.5
C.4
D.3
2.到平面内不在同一直线上的三个点A,B,C的距离相等的点有
1
个.
3.如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=
15
.
4.如图,直线AD是线段BC的垂直平分线.求证:∠ABD=∠ACD.
训
固
练
证明:∵AD是BC的垂直平分线,
∴AB=AC,BD=DC.
∵AD=AD,
∴△ABD≌△ACD.
∴∠ABD=∠ACD.
5、如图,AD⊥
BC,BD
=DC,点
C
在
AE
的垂直平分线上,AB,AC,CE
的长度有什么关系?AB
+
BD
与
DE
有什么关系?
A
B
C
D
E
解:∵ AD⊥
BC,BD
=
DC,
∴ AD
是BC
的垂直平分线,
∴ AB
=
AC.
∵ 点
C
在AE
的垂直平分线上,
∴ AC
=
CE.
∴ AB
=
AC
=
CE.
∵ AB
=
CE,BD
=
DC,
∴ AB
+
BD
=
CD
+CE.
即 AB
+
BD
=
DE
.
1.
定理
线段垂直平分线上的点到这条线段两个端点距离相等.
∵AC=BC,MN⊥AB,P
是
MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
2.
逆定理
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∵PA=PB(已知),
∴点
P
在
AB
的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
五、归纳小结
第1课时
线段的垂直平分线的性质与判定
13.1.2
线段的垂直平分线的性质
A
B
l
P1
P2
P3
相等.
你能用不同的方法验证这一结论吗?
一、提出问题,思考引入
证明:“线段垂直平分线上的点到线段两端点的距离相等.
”
已知:如图,直线
l
⊥
AB,垂足为
C,AC=CB,点
P
在
l
上.
求证:PA
=PB.
证明:∵ l
⊥AB,
∴
∠PCA
=∠PCB.
又
AC
=
CB,PC
=
PC,
∴
△PCA
≌△PCB(SAS).
∴
PA
=
PB.
A
B
P
C
l
二、合作交流,探究新知
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
用符号语言表示为:
∵
CA
=
CB,l
⊥
AB,
∴
PA
=
PB.
结论:
A
B
P
C
l
反过来,如果
PA
=
PB,那么点
P
是否在线段
AB
的
垂直平分线上呢?
点
P
在线段
AB
的垂直平分线上.
P
A
B
C
二、合作交流,探究新知
已知:如图,PA
=
PB.
求证:点
P
在线段
AB
的垂直平分线上.
证明:过点
P
作线段
AB
的垂线
PC,
垂足为
C.则∠PCA
=∠PCB
=
90°.
在
Rt△PCA
和
Rt△PCB
中,
∵ PA
=
PB,PC
=
PC,
∴
Rt△PCA
≌
Rt△PCB(HL).
∴
AC
=
BC.
又
PC⊥AB,
∴
点
P
在线段
AB
的垂直平分线上.
P
A
B
C
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
用数学符号表示为:
∵ PA
=
PB,
∴ 点
P
在
AB
的垂直平分线上.
结论:
P
A
B
C
你能再找一些到线段
AB
两端点的距离相等的点吗?能找到多少个到线段
AB
两端点距离相等的点?这些点能组成什么几何图形?
在线段
AB
的垂直平分线
l
上的点与
A,B
的距离都相等;反过来,与
A,B
的距离相等的点都在直线
l上,所以直线l
可以看成与两点
A、B
的距离相等的所有点的集合.
P
A
B
C
二、合作交流,探究新知
尺规作图:
如何用尺规作图的方法经过直线外一点作已知直线的垂线?
C
A
B
D
K
F
E
大家拿出圆规和直尺,按照教材中的作法一起来做一做.
三、运用新知
我们已能用尺规完成:
那么利用尺规还能解决什么作图问题呢?
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
(4)经过已知直线外一点作这条直线的垂线.
三、运用新知
例1 如图,AB=AC=8
cm,AB的垂直平分线交AC于点D.若△ADB的周长为18
cm,求DC的长.
讲
校
坛
解:∵DM是AB的垂直平分线,
∴AD=BD.
设CD的长为x,则AD=AC-CD=8-x.
∵C△ADB=AB+AD+BD=8+(8-x)+(8-x)=18,
∴x=3,即CD的长为3
cm.
【点拨】 由线段垂直平分线的性质得AD=BD进而求解.
三、运用新知
训
固
四、巩固新知
1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为(
B
)
A.6
B.5
C.4
D.3
2.到平面内不在同一直线上的三个点A,B,C的距离相等的点有
1
个.
3.如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=
15
.
4.如图,直线AD是线段BC的垂直平分线.求证:∠ABD=∠ACD.
训
固
练
证明:∵AD是BC的垂直平分线,
∴AB=AC,BD=DC.
∵AD=AD,
∴△ABD≌△ACD.
∴∠ABD=∠ACD.
5、如图,AD⊥
BC,BD
=DC,点
C
在
AE
的垂直平分线上,AB,AC,CE
的长度有什么关系?AB
+
BD
与
DE
有什么关系?
A
B
C
D
E
解:∵ AD⊥
BC,BD
=
DC,
∴ AD
是BC
的垂直平分线,
∴ AB
=
AC.
∵ 点
C
在AE
的垂直平分线上,
∴ AC
=
CE.
∴ AB
=
AC
=
CE.
∵ AB
=
CE,BD
=
DC,
∴ AB
+
BD
=
CD
+CE.
即 AB
+
BD
=
DE
.
1.
定理
线段垂直平分线上的点到这条线段两个端点距离相等.
∵AC=BC,MN⊥AB,P
是
MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
2.
逆定理
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∵PA=PB(已知),
∴点
P
在
AB
的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
五、归纳小结
