2.2.4 公式法 同步练习(含解析)
文档属性
| 名称 | 2.2.4 公式法 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 998.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 19:37:55 | ||
图片预览




文档简介
2.2 一元二次方程的解法
第4课时 公式法
一、选择题
1.用公式法解方程-x2+3x=1时,需先确定a,b,c的值,则a,b,c的值依次为( )
A.-1,3,-1
B.1,3,-1
C.-1,-3,-1
D.-1,3,1
2.用公式法解方程x2+5x-5=0,下列代入公式正确的是( )
A.x=
B.x=
C.x=
D.x=
3.【2020·贵阳十九中期末】一元二次方程x2+4x=2中,b2-4ac的值应是( )
A.64
B.-64
C.32
D.-32
4.方程(x+1)(x-3)=5的解是
( B )
A.x1=1,x2=-3
B.x1=4,x2=-2
C.x1=-1,x2=3
D.x1=-4,x2=2
5.已知方程2x2-6x+3=0较小的根为p,方程2x2-2x-1=0较大的根为q,则p+q等于( )
A.3
B.2
C.1
D.2
6.用公式法解方程(x+2)2=6(x+2)-4时,b2-4ac的值为( )
A.52
B.32
C.20
D.-12
7.【2020·临沂】一元二次方程x2-4x-8=0的解是( )
A.x1=-2+2,x2=-2-2
B.x1=2+2,x2=2-2
C.x1=2+2,x2=2-2
D.x1=2,x2=-2
8.用公式法解方程(x+2)2=6(x+2)-4时,b2-4ac的值为( )
A.52
B.32
C.20
D.-12
9.以x=(b2+4c≥0)为根的一元二次方程可能是( )
A.x2+bx+c=0
B.x2+bx-c=0
C.x2-bx+c=0
D.x2-bx-c=0
10.若x2+px+q=0的两个实数根中较大的一个根是k(k≠0),则代数式p-的值是( )
A.k
B.-k
C.2k
D.-2k
11.当x=(a≠0,b2-4ac>0)时,代数式ax2+bx+c的值是( )
A.0
B.
C.-
D.
12.若方程x2+bx+c=0的两个实数根中较小的一个根是m(m≠0),则b+=
(
)
A.m
B.-m
C.2m
D.-2m
二、填空题
13.一元二次方程ax2+bx+c=0(a≠0)在b2-4ac≥0的条件下,它的根为__________________.我们通常把这个式子叫作一元二次方程ax2+bx+c=0(a≠0)的求根公式.
14.运用一元二次方程的__________可以直接求出每一个一元二次方程的根,这种解一元二次方程的方法叫作公式法.
15.方程x2+px+q=0(其中p2-4q≥0)的两个实数根分别为x1=________________,x2=_________________.
16.若在实数范围内定义一种运算“﹡”,使a﹡b=(a+1)2-ab,则方程(x+2)﹡5=0的解为________________________________.
17.用公式法解方程:3y2+4y=3y+2.
解:方程化为一般形式,得__________________.
a=______,b=______,c=______,Δ=b2-4ac=______.
方程____________的实数根,为
y==__________,
即y1=________,y2=________.
18.已知关于x的方程(m2-1)x2+2(m-1)x+1=0有实数根,则m的取值范围是
.
三、解答题
19.用公式法解一元二次方程.
(1)x2-x=-2;
(2)【中考·常德】x2-3x-2=0;
(3)【2020·无锡】x2+x-1=0;
(4)【2021·达州渠县期末】x2-2x+1=0;
(5)3x2+3=4x.
(6)2x2=9x-8;
(7)2y(y-1)+3=(y+1)2.
(8)(x-2)(3x-5)=1
20.用公式法解方程:2x2+7x=4.
解:∵a=2,b=7,c=4,
∴b2-4ac=72-4×2×4=17.
∴x=,
即x1=,x2=.
上述解法是否正确?若不正确,请指出错误并改正.
21.当x为何值时,3x2+4x-8的值和2x2-1的值相等?
22.用公式法解关于x的方程:x2-3mx+2m2-mn-n2=0.
23.【2020·广东】已知关于x,y的方程组与的解相同.
(1)求a,b的值;
(2)若一个三角形的一条边的长为2,另外两条边的长是关于x的方程x2+ax+b=0的解.试判断该三角形的形状,并说明理由.
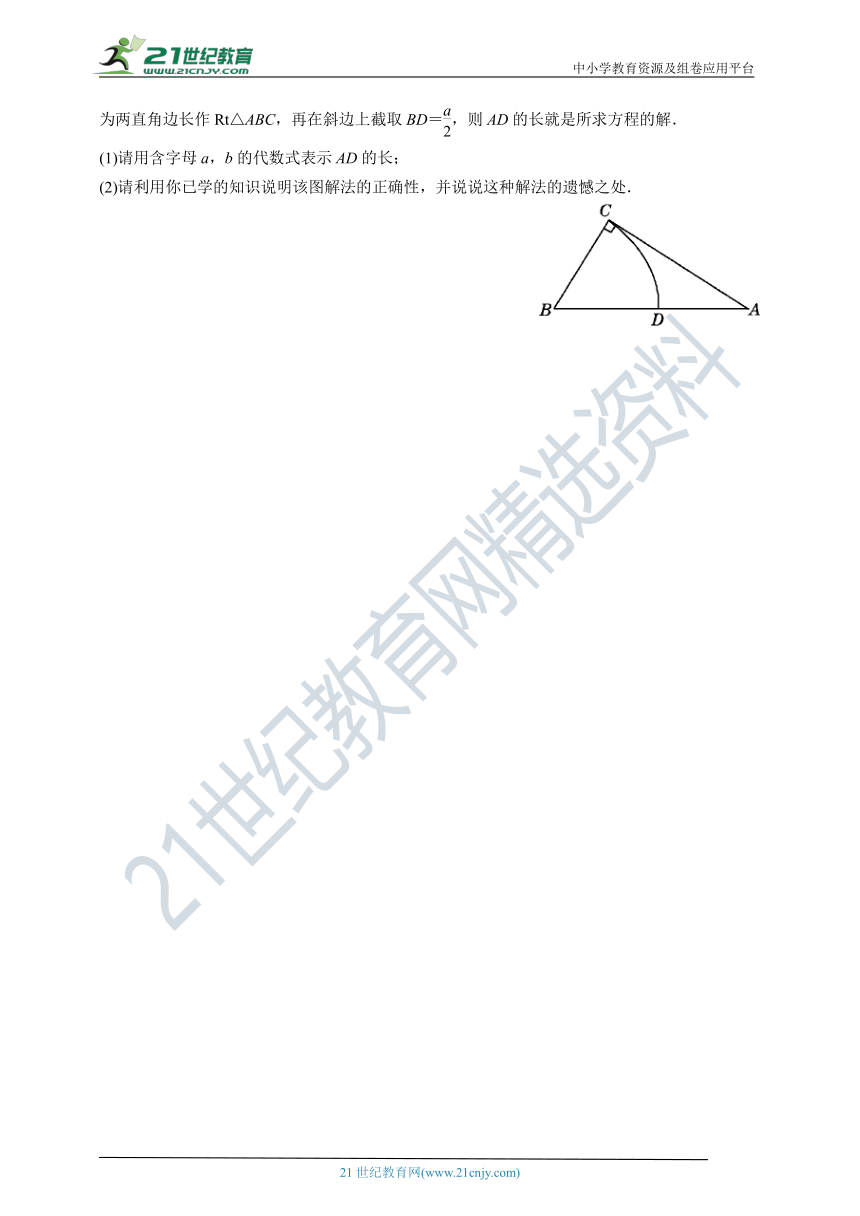
24.在欧几里得的《几何原本》中,形如x2+ax=b2(a>0,b>0)的方程的图解法是:如图,以和b为两直角边长作Rt△ABC,再在斜边上截取BD=,则AD的长就是所求方程的解.
(1)请用含字母a,b的代数式表示AD的长;
(2)请利用你已学的知识说明该图解法的正确性,并说说这种解法的遗憾之处.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.用公式法解方程-x2+3x=1时,需先确定a,b,c的值,则a,b,c的值依次为( A )
A.-1,3,-1
B.1,3,-1
C.-1,-3,-1
D.-1,3,1
2.用公式法解方程x2+5x-5=0,下列代入公式正确的是( C )
A.x=
B.x=
C.x=
D.x=
3.【2020·贵阳十九中期末】一元二次方程x2+4x=2中,b2-4ac的值应是( A )
A.64
B.-64
C.32
D.-32
4.方程(x+1)(x-3)=5的解是
( B )
A.x1=1,x2=-3
B.x1=4,x2=-2
C.x1=-1,x2=3
D.x1=-4,x2=2
5.已知方程2x2-6x+3=0较小的根为p,方程2x2-2x-1=0较大的根为q,则p+q等于( B )
A.3
B.2
C.1
D.2
6.用公式法解方程(x+2)2=6(x+2)-4时,b2-4ac的值为( C )
A.52
B.32
C.20
D.-12
7.【2020·临沂】一元二次方程x2-4x-8=0的解是( B )
A.x1=-2+2,x2=-2-2
B.x1=2+2,x2=2-2
C.x1=2+2,x2=2-2
D.x1=2,x2=-2
8.用公式法解方程(x+2)2=6(x+2)-4时,b2-4ac的值为( C )
A.52
B.32
C.20
D.-12
9.以x=(b2+4c≥0)为根的一元二次方程可能是( D )
A.x2+bx+c=0
B.x2+bx-c=0
C.x2-bx+c=0
D.x2-bx-c=0
10.若x2+px+q=0的两个实数根中较大的一个根是k(k≠0),则代数式p-的值是( D )
A.k
B.-k
C.2k
D.-2k
11.当x=(a≠0,b2-4ac>0)时,代数式ax2+bx+c的值是( A )
A.0
B.
C.-
D.
12.若方程x2+bx+c=0的两个实数根中较小的一个根是m(m≠0),则b+=
(D)
A.m
B.-m
C.2m
D.-2m
二、填空题
13.一元二次方程ax2+bx+c=0(a≠0)在b2-4ac≥0的条件下,它的根为__________________.我们通常把这个式子叫作一元二次方程ax2+bx+c=0(a≠0)的求根公式.
【答案】x=
14.运用一元二次方程的__________可以直接求出每一个一元二次方程的根,这种解一元二次方程的方法叫作公式法.
【答案】求根公式
15.方程x2+px+q=0(其中p2-4q≥0)的两个实数根分别为x1=________________,x2=_________________.
【答案】
16.若在实数范围内定义一种运算“﹡”,使a﹡b=(a+1)2-ab,则方程(x+2)﹡5=0的解为________________________________.
【答案】x1=,x2=
17.用公式法解方程:3y2+4y=3y+2.
解:方程化为一般形式,得__________________.
a=______,b=______,c=______,Δ=b2-4ac=______.
方程____________的实数根,为
y==__________,
即y1=________,y2=________.
【答案】3y2+y-2=0
3
1
-2
25
有两个不等
-1
18.已知关于x的方程(m2-1)x2+2(m-1)x+1=0有实数根,则m的取值范围是 m<1 .
提示:①当方程(m2-1)x2+2(m-1)x+1=0为一元二次方程时,m2-1≠0,即m≠±1.∵关于x的方程(m2-1)x2+2(m-1)x+1=0有实数根,∴Δ=[2(m-1)]2-4(m2-1)=-8m+8≥0,解得m≤1,∴m<1且m≠-1.②当方程(m2-1)x2+2(m-1)x+1=0为一元一次方程时,m2-1=0且2(m-1)≠0,则m=-1.综上所述,m<1时方程有实数根.
三、解答题
19.用公式法解一元二次方程.
(1)x2-x=-2;
解:方程无解.
(2)【中考·常德】x2-3x-2=0;
解:∵a=1,b=-3,c=-2,
∴b2-4ac=(-3)2-4×1×(-2)=9+8=17.
∴x==,
∴x1=,x2=.
(3)【2020·无锡】x2+x-1=0;
解:∵a=1,b=1,c=-1,
∴b2-4ac=12-4×1×(-1)=5,
∴x=,
∴x1=,x2=.
(4)【2021·达州渠县期末】x2-2x+1=0;
解:∵a=1,b=-2,c=1,
∴b2-4ac=(-2
)2-4×1×1=8-4=4.
∴x===±1.
∴x1=+1,x2=-1.
(5)3x2+3=4x.
解:方程可整理为3x2-4x+3=0,
∵a=3,b=-4,c=3,
∴b2-4ac=(-4)2-4×3×3<0,
∴方程无实数根.
(6)2x2=9x-8;
解:移项,得2x2-9x+8=0.
∴a=2,b=-9,c=8,
∴b2-4ac=(-9)2-4×2×8=17,
∴x1=,x2=.
(7)2y(y-1)+3=(y+1)2.
解:由原方程,得2y2-2y+3=y2+2y+1,
即y2-4y+2=0,
∴a=1,b=-4,c=2,
∴b2-4ac=(-4)2-4×1×2=8>0.
∴y=,
∴y1=2+,y2=2-.
(8)(x-2)(3x-5)=1
解:将方程化为一般形式3x2-11x+9=0,a=3,b=-11,c=9,
b2-4ac=(-11)2-4×3×9=13>0,
∴x=,
∴x1=,x2=.
20.用公式法解方程:2x2+7x=4.
解:∵a=2,b=7,c=4,
∴b2-4ac=72-4×2×4=17.
∴x=,
即x1=,x2=.
上述解法是否正确?若不正确,请指出错误并改正.
解:不正确.错误原因:没有将方程化成一般形式,造成常数项c的符号错误.
正解:移项,得2x2+7x-4=0,
∴a=2,b=7,c=-4,
∴b2-4ac=72-4×2×(-4)=81.
∴x==.
即x1=,x2=-4.
21.当x为何值时,3x2+4x-8的值和2x2-1的值相等?
解:根据题意得:3x2+4x-8=2x2-1,
即x2+4x-7=0,
∴a=1,b=4,c=-7,
∴b2-4ac=16+28=44>0,
则x==-2±.
22.用公式法解关于x的方程:x2-3mx+2m2-mn-n2=0.
解:由题意可知a=1,b=-3m,c=2m2-mn-n2,
∵b2-4ac=9m2-4(2m2-mn-n2)=m2+4mn+4n2=(m+2n)2≥0,
∴x=,
解得x1=2m+n,x2=m-n.
23.【2020·广东】已知关于x,y的方程组与的解相同.
(1)求a,b的值;
解:由题意,得关于x,y的方程组的相同解就是方程组的解,
解得代入原方程组得a=-4,b=12.
(2)若一个三角形的一条边的长为2,另外两条边的长是关于x的方程x2+ax+b=0的解.试判断该三角形的形状,并说明理由.
解:该三角形为等腰直角三角形.
理由:当a=-4,b=12时,关于x的方程x2+ax+b=0就变为x2-4x+12=0,
解得x1=x2=2.
又∵(2)2+(2)2=(2)2,
∴以2,2,2为边的三角形是等腰直角三角形.
24.在欧几里得的《几何原本》中,形如x2+ax=b2(a>0,b>0)的方程的图解法是:如图,以和b为两直角边长作Rt△ABC,再在斜边上截取BD=,则AD的长就是所求方程的解.
(1)请用含字母a,b的代数式表示AD的长;
解:∵∠C=90°,BC=,
AC=b,∴AB=,
∴AD=-=.
(2)请利用你已学的知识说明该图解法的正确性,并说说这种解法的遗憾之处.
解:用求根公式求得:
x1=,x2=.
正确性:AD的长就是方程的正根.
中小学教育资源及组卷应用平台
遗憾之处:图解法不能表示方程的负根.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第4课时 公式法
一、选择题
1.用公式法解方程-x2+3x=1时,需先确定a,b,c的值,则a,b,c的值依次为( )
A.-1,3,-1
B.1,3,-1
C.-1,-3,-1
D.-1,3,1
2.用公式法解方程x2+5x-5=0,下列代入公式正确的是( )
A.x=
B.x=
C.x=
D.x=
3.【2020·贵阳十九中期末】一元二次方程x2+4x=2中,b2-4ac的值应是( )
A.64
B.-64
C.32
D.-32
4.方程(x+1)(x-3)=5的解是
( B )
A.x1=1,x2=-3
B.x1=4,x2=-2
C.x1=-1,x2=3
D.x1=-4,x2=2
5.已知方程2x2-6x+3=0较小的根为p,方程2x2-2x-1=0较大的根为q,则p+q等于( )
A.3
B.2
C.1
D.2
6.用公式法解方程(x+2)2=6(x+2)-4时,b2-4ac的值为( )
A.52
B.32
C.20
D.-12
7.【2020·临沂】一元二次方程x2-4x-8=0的解是( )
A.x1=-2+2,x2=-2-2
B.x1=2+2,x2=2-2
C.x1=2+2,x2=2-2
D.x1=2,x2=-2
8.用公式法解方程(x+2)2=6(x+2)-4时,b2-4ac的值为( )
A.52
B.32
C.20
D.-12
9.以x=(b2+4c≥0)为根的一元二次方程可能是( )
A.x2+bx+c=0
B.x2+bx-c=0
C.x2-bx+c=0
D.x2-bx-c=0
10.若x2+px+q=0的两个实数根中较大的一个根是k(k≠0),则代数式p-的值是( )
A.k
B.-k
C.2k
D.-2k
11.当x=(a≠0,b2-4ac>0)时,代数式ax2+bx+c的值是( )
A.0
B.
C.-
D.
12.若方程x2+bx+c=0的两个实数根中较小的一个根是m(m≠0),则b+=
(
)
A.m
B.-m
C.2m
D.-2m
二、填空题
13.一元二次方程ax2+bx+c=0(a≠0)在b2-4ac≥0的条件下,它的根为__________________.我们通常把这个式子叫作一元二次方程ax2+bx+c=0(a≠0)的求根公式.
14.运用一元二次方程的__________可以直接求出每一个一元二次方程的根,这种解一元二次方程的方法叫作公式法.
15.方程x2+px+q=0(其中p2-4q≥0)的两个实数根分别为x1=________________,x2=_________________.
16.若在实数范围内定义一种运算“﹡”,使a﹡b=(a+1)2-ab,则方程(x+2)﹡5=0的解为________________________________.
17.用公式法解方程:3y2+4y=3y+2.
解:方程化为一般形式,得__________________.
a=______,b=______,c=______,Δ=b2-4ac=______.
方程____________的实数根,为
y==__________,
即y1=________,y2=________.
18.已知关于x的方程(m2-1)x2+2(m-1)x+1=0有实数根,则m的取值范围是
.
三、解答题
19.用公式法解一元二次方程.
(1)x2-x=-2;
(2)【中考·常德】x2-3x-2=0;
(3)【2020·无锡】x2+x-1=0;
(4)【2021·达州渠县期末】x2-2x+1=0;
(5)3x2+3=4x.
(6)2x2=9x-8;
(7)2y(y-1)+3=(y+1)2.
(8)(x-2)(3x-5)=1
20.用公式法解方程:2x2+7x=4.
解:∵a=2,b=7,c=4,
∴b2-4ac=72-4×2×4=17.
∴x=,
即x1=,x2=.
上述解法是否正确?若不正确,请指出错误并改正.
21.当x为何值时,3x2+4x-8的值和2x2-1的值相等?
22.用公式法解关于x的方程:x2-3mx+2m2-mn-n2=0.
23.【2020·广东】已知关于x,y的方程组与的解相同.
(1)求a,b的值;
(2)若一个三角形的一条边的长为2,另外两条边的长是关于x的方程x2+ax+b=0的解.试判断该三角形的形状,并说明理由.
24.在欧几里得的《几何原本》中,形如x2+ax=b2(a>0,b>0)的方程的图解法是:如图,以和b为两直角边长作Rt△ABC,再在斜边上截取BD=,则AD的长就是所求方程的解.
(1)请用含字母a,b的代数式表示AD的长;
(2)请利用你已学的知识说明该图解法的正确性,并说说这种解法的遗憾之处.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.用公式法解方程-x2+3x=1时,需先确定a,b,c的值,则a,b,c的值依次为( A )
A.-1,3,-1
B.1,3,-1
C.-1,-3,-1
D.-1,3,1
2.用公式法解方程x2+5x-5=0,下列代入公式正确的是( C )
A.x=
B.x=
C.x=
D.x=
3.【2020·贵阳十九中期末】一元二次方程x2+4x=2中,b2-4ac的值应是( A )
A.64
B.-64
C.32
D.-32
4.方程(x+1)(x-3)=5的解是
( B )
A.x1=1,x2=-3
B.x1=4,x2=-2
C.x1=-1,x2=3
D.x1=-4,x2=2
5.已知方程2x2-6x+3=0较小的根为p,方程2x2-2x-1=0较大的根为q,则p+q等于( B )
A.3
B.2
C.1
D.2
6.用公式法解方程(x+2)2=6(x+2)-4时,b2-4ac的值为( C )
A.52
B.32
C.20
D.-12
7.【2020·临沂】一元二次方程x2-4x-8=0的解是( B )
A.x1=-2+2,x2=-2-2
B.x1=2+2,x2=2-2
C.x1=2+2,x2=2-2
D.x1=2,x2=-2
8.用公式法解方程(x+2)2=6(x+2)-4时,b2-4ac的值为( C )
A.52
B.32
C.20
D.-12
9.以x=(b2+4c≥0)为根的一元二次方程可能是( D )
A.x2+bx+c=0
B.x2+bx-c=0
C.x2-bx+c=0
D.x2-bx-c=0
10.若x2+px+q=0的两个实数根中较大的一个根是k(k≠0),则代数式p-的值是( D )
A.k
B.-k
C.2k
D.-2k
11.当x=(a≠0,b2-4ac>0)时,代数式ax2+bx+c的值是( A )
A.0
B.
C.-
D.
12.若方程x2+bx+c=0的两个实数根中较小的一个根是m(m≠0),则b+=
(D)
A.m
B.-m
C.2m
D.-2m
二、填空题
13.一元二次方程ax2+bx+c=0(a≠0)在b2-4ac≥0的条件下,它的根为__________________.我们通常把这个式子叫作一元二次方程ax2+bx+c=0(a≠0)的求根公式.
【答案】x=
14.运用一元二次方程的__________可以直接求出每一个一元二次方程的根,这种解一元二次方程的方法叫作公式法.
【答案】求根公式
15.方程x2+px+q=0(其中p2-4q≥0)的两个实数根分别为x1=________________,x2=_________________.
【答案】
16.若在实数范围内定义一种运算“﹡”,使a﹡b=(a+1)2-ab,则方程(x+2)﹡5=0的解为________________________________.
【答案】x1=,x2=
17.用公式法解方程:3y2+4y=3y+2.
解:方程化为一般形式,得__________________.
a=______,b=______,c=______,Δ=b2-4ac=______.
方程____________的实数根,为
y==__________,
即y1=________,y2=________.
【答案】3y2+y-2=0
3
1
-2
25
有两个不等
-1
18.已知关于x的方程(m2-1)x2+2(m-1)x+1=0有实数根,则m的取值范围是 m<1 .
提示:①当方程(m2-1)x2+2(m-1)x+1=0为一元二次方程时,m2-1≠0,即m≠±1.∵关于x的方程(m2-1)x2+2(m-1)x+1=0有实数根,∴Δ=[2(m-1)]2-4(m2-1)=-8m+8≥0,解得m≤1,∴m<1且m≠-1.②当方程(m2-1)x2+2(m-1)x+1=0为一元一次方程时,m2-1=0且2(m-1)≠0,则m=-1.综上所述,m<1时方程有实数根.
三、解答题
19.用公式法解一元二次方程.
(1)x2-x=-2;
解:方程无解.
(2)【中考·常德】x2-3x-2=0;
解:∵a=1,b=-3,c=-2,
∴b2-4ac=(-3)2-4×1×(-2)=9+8=17.
∴x==,
∴x1=,x2=.
(3)【2020·无锡】x2+x-1=0;
解:∵a=1,b=1,c=-1,
∴b2-4ac=12-4×1×(-1)=5,
∴x=,
∴x1=,x2=.
(4)【2021·达州渠县期末】x2-2x+1=0;
解:∵a=1,b=-2,c=1,
∴b2-4ac=(-2
)2-4×1×1=8-4=4.
∴x===±1.
∴x1=+1,x2=-1.
(5)3x2+3=4x.
解:方程可整理为3x2-4x+3=0,
∵a=3,b=-4,c=3,
∴b2-4ac=(-4)2-4×3×3<0,
∴方程无实数根.
(6)2x2=9x-8;
解:移项,得2x2-9x+8=0.
∴a=2,b=-9,c=8,
∴b2-4ac=(-9)2-4×2×8=17,
∴x1=,x2=.
(7)2y(y-1)+3=(y+1)2.
解:由原方程,得2y2-2y+3=y2+2y+1,
即y2-4y+2=0,
∴a=1,b=-4,c=2,
∴b2-4ac=(-4)2-4×1×2=8>0.
∴y=,
∴y1=2+,y2=2-.
(8)(x-2)(3x-5)=1
解:将方程化为一般形式3x2-11x+9=0,a=3,b=-11,c=9,
b2-4ac=(-11)2-4×3×9=13>0,
∴x=,
∴x1=,x2=.
20.用公式法解方程:2x2+7x=4.
解:∵a=2,b=7,c=4,
∴b2-4ac=72-4×2×4=17.
∴x=,
即x1=,x2=.
上述解法是否正确?若不正确,请指出错误并改正.
解:不正确.错误原因:没有将方程化成一般形式,造成常数项c的符号错误.
正解:移项,得2x2+7x-4=0,
∴a=2,b=7,c=-4,
∴b2-4ac=72-4×2×(-4)=81.
∴x==.
即x1=,x2=-4.
21.当x为何值时,3x2+4x-8的值和2x2-1的值相等?
解:根据题意得:3x2+4x-8=2x2-1,
即x2+4x-7=0,
∴a=1,b=4,c=-7,
∴b2-4ac=16+28=44>0,
则x==-2±.
22.用公式法解关于x的方程:x2-3mx+2m2-mn-n2=0.
解:由题意可知a=1,b=-3m,c=2m2-mn-n2,
∵b2-4ac=9m2-4(2m2-mn-n2)=m2+4mn+4n2=(m+2n)2≥0,
∴x=,
解得x1=2m+n,x2=m-n.
23.【2020·广东】已知关于x,y的方程组与的解相同.
(1)求a,b的值;
解:由题意,得关于x,y的方程组的相同解就是方程组的解,
解得代入原方程组得a=-4,b=12.
(2)若一个三角形的一条边的长为2,另外两条边的长是关于x的方程x2+ax+b=0的解.试判断该三角形的形状,并说明理由.
解:该三角形为等腰直角三角形.
理由:当a=-4,b=12时,关于x的方程x2+ax+b=0就变为x2-4x+12=0,
解得x1=x2=2.
又∵(2)2+(2)2=(2)2,
∴以2,2,2为边的三角形是等腰直角三角形.
24.在欧几里得的《几何原本》中,形如x2+ax=b2(a>0,b>0)的方程的图解法是:如图,以和b为两直角边长作Rt△ABC,再在斜边上截取BD=,则AD的长就是所求方程的解.
(1)请用含字母a,b的代数式表示AD的长;
解:∵∠C=90°,BC=,
AC=b,∴AB=,
∴AD=-=.
(2)请利用你已学的知识说明该图解法的正确性,并说说这种解法的遗憾之处.
解:用求根公式求得:
x1=,x2=.
正确性:AD的长就是方程的正根.
中小学教育资源及组卷应用平台
遗憾之处:图解法不能表示方程的负根.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
