北师大版2021--2022七年级(上)数学第三单元质量检测试卷B(含解析)
文档属性
| 名称 | 北师大版2021--2022七年级(上)数学第三单元质量检测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 995.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-01 20:03:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2021-2022学年七年级(上)第三章整式及其加减检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
在式子
,,,,,,
中,是整式的有
A.
个
B.
个
C.
个
D.
个
2.
下列各式:,,,,,其中整式有
A.
个
B.
个
C.
个
D.
个
3.
假设每个人做某项工作的工作效率相同,
个人共同做该项工作,
天可以完成.若增加
人,则完成该项工作需要
天.
A.
B.
C.
D.
4.
关于
的代数式
,当
取值分别为
,,,
时,对应的代数式的值如下表:
则
的值是
A.
B.
C.
D.
5.
某品牌冰箱的进价为每台
元,现提高进价的
进行销售,则这种冰箱的售价为
A.
元
B.
元
C.
元
D.
元
6.
多项式
的次数和一次项系数分别是
A.
,
B.
,
C.
,
D.
,
7.
下列式子中,书写格式规范的是
A.
B.
C.
D.
8.
下列计算中正确的是
A.
B.
C.
D.
9.
对多项式
进行添括号,正确的是
A.
B.
C.
D.
10.
某校组织若干师生到恩施大峡谷进行社会实践活动,若学校租用
座的客车
辆,则余下
人无座位;若租用
座的客车则可少租用
辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是
A.
B.
C.
D.
11.
定义运算
:,如
,那么
的值为
A.
B.
C.
D.
12.
要使
始终成立,则
,,
的值分别是
A.
,,
B.
,,
C.
,,
D.
,,
二、填空题(共6小题;每小题4分,共24分)
13.
统称整式.
14.
三个连续整数,若最大的一个整数为
,则另外两个整数可表示为
和
.
15.
化简:
()
;
()
;
()
;
()
.
16.
对于正数
,规定
,例如:,,,,,利用以上规律计算:
的值为
.
17.
有一列数,按一定规律排列为
,,,,,,,其中某三个相邻数的积是
,则这三个数的和是
.
18.
某天数学课上老师讲了整式的加减运算,小颖回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:,空格的地方被墨水弄脏了,请问空格中的一项是
.
三、解答题(共7小题;共60分)
19.
(8分)下列各式子中,哪些是单项式
,,,,,,.
20.
(8分)
是不为
的有理数,我们把
称为
的差倒数,如:
的差倒数是
,
的差倒数是
.已知
,
是
的差倒数,
是
的差倒数,
是
的差倒数,,依此类推,则
等于多少
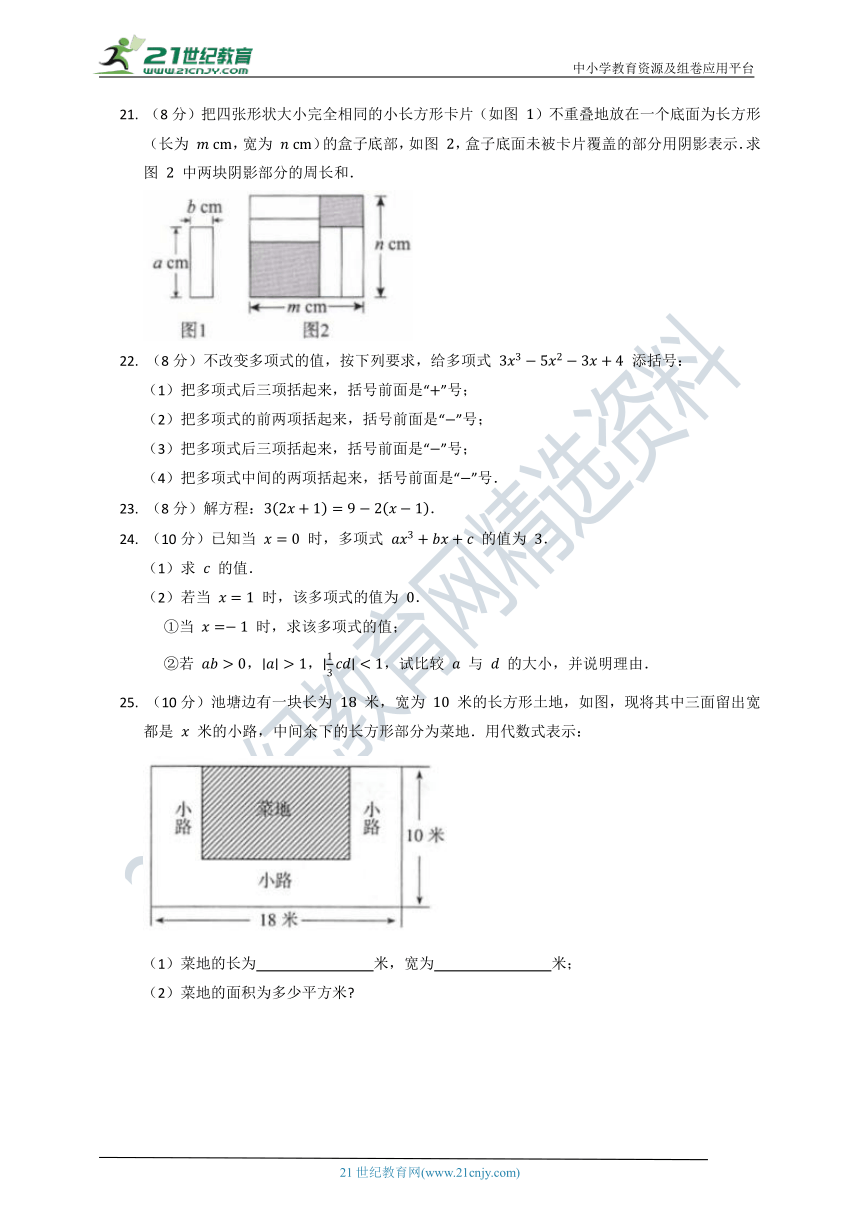
21.
(8分)把四张形状大小完全相同的小长方形卡片(如图
)不重叠地放在一个底面为长方形(长为
,宽为
)的盒子底部,如图
,盒子底面未被卡片覆盖的部分用阴影表示.求图
中两块阴影部分的周长和.
22.
(8分)不改变多项式的值,按下列要求,给多项式
添括号:
(1)把多项式后三项括起来,括号前面是“”号;
(2)把多项式的前两项括起来,括号前面是“”号;
(3)把多项式后三项括起来,括号前面是“”号;
(4)把多项式中间的两项括起来,括号前面是“”号.
23.
(8分)解方程:.
24.
(10分)已知当
时,多项式
的值为
.
(1)求
的值.
(2)若当
时,该多项式的值为
.
①当
时,求该多项式的值;
②若
,,,试比较
与
的大小,并说明理由.
25.
(10分)池塘边有一块长为
米,宽为
米的长方形土地,如图,现将其中三面留出宽都是
米的小路,中间余下的长方形部分为菜地.用代数式表示:
(1)菜地的长为
米,宽为
米;
(2)菜地的面积为多少平方米
答案
第一部分
1.
D
2.
C
【解析】
的分母中含有未知数,不是整式,其余的都是整式,有
个.
3.
C
4.
C
5.
D
6.
D
7.
C
8.
D
9.
D
10.
C
【解析】因为学校租用
座的客车
辆,则余下
人无座位,所以师生的总人数为
.又因为租用
座的客车则可少租用
辆,所以乘坐最后一辆
座客车的人数为
.
11.
B
【解析】由已知得,,,,,
,
,,,,
则
.
12.
D
【解析】
,,,
,,.
第二部分
13.
单项式与多项式
14.
,
15.
,,,
16.
【解析】
17.
【解析】
一列数为
,,,,,,,
这列数的第
个数可以表示为
,
其中某三个相邻数的积是
,
设这三个相邻的数分别为
,,,
则
,
,
,解得
,
这三个相邻的数分别为
,,,
这三个数的和是
18.
【解析】依题意,空格中的一项是
第三部分
19.
单项式:,,,,.
20.
.
21.
.
22.
(1)
.
(2)
.
(3)
.
(4)
.
23.
去括号,得
移项,得
合并同类项,得
系数化为
,得
24.
(1)
把
代入
,得
.
(2)
①把
代入
,得
.
所以
.
把
代入
,得
.
②
,理由如下:
因为
,
所以
,
同号.
由①知
,
所以
,.
因为
,
所以
.
因为
,且
,
所以
.
所以
.
所以
.
25.
(1)
;
(2)
由()可得菜地的面积为
平方米.
米
厘米,
覆盖
个整数点.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
北师大版2021-2022学年七年级(上)第三章整式及其加减检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
在式子
,,,,,,
中,是整式的有
A.
个
B.
个
C.
个
D.
个
2.
下列各式:,,,,,其中整式有
A.
个
B.
个
C.
个
D.
个
3.
假设每个人做某项工作的工作效率相同,
个人共同做该项工作,
天可以完成.若增加
人,则完成该项工作需要
天.
A.
B.
C.
D.
4.
关于
的代数式
,当
取值分别为
,,,
时,对应的代数式的值如下表:
则
的值是
A.
B.
C.
D.
5.
某品牌冰箱的进价为每台
元,现提高进价的
进行销售,则这种冰箱的售价为
A.
元
B.
元
C.
元
D.
元
6.
多项式
的次数和一次项系数分别是
A.
,
B.
,
C.
,
D.
,
7.
下列式子中,书写格式规范的是
A.
B.
C.
D.
8.
下列计算中正确的是
A.
B.
C.
D.
9.
对多项式
进行添括号,正确的是
A.
B.
C.
D.
10.
某校组织若干师生到恩施大峡谷进行社会实践活动,若学校租用
座的客车
辆,则余下
人无座位;若租用
座的客车则可少租用
辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是
A.
B.
C.
D.
11.
定义运算
:,如
,那么
的值为
A.
B.
C.
D.
12.
要使
始终成立,则
,,
的值分别是
A.
,,
B.
,,
C.
,,
D.
,,
二、填空题(共6小题;每小题4分,共24分)
13.
统称整式.
14.
三个连续整数,若最大的一个整数为
,则另外两个整数可表示为
和
.
15.
化简:
()
;
()
;
()
;
()
.
16.
对于正数
,规定
,例如:,,,,,利用以上规律计算:
的值为
.
17.
有一列数,按一定规律排列为
,,,,,,,其中某三个相邻数的积是
,则这三个数的和是
.
18.
某天数学课上老师讲了整式的加减运算,小颖回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:,空格的地方被墨水弄脏了,请问空格中的一项是
.
三、解答题(共7小题;共60分)
19.
(8分)下列各式子中,哪些是单项式
,,,,,,.
20.
(8分)
是不为
的有理数,我们把
称为
的差倒数,如:
的差倒数是
,
的差倒数是
.已知
,
是
的差倒数,
是
的差倒数,
是
的差倒数,,依此类推,则
等于多少
21.
(8分)把四张形状大小完全相同的小长方形卡片(如图
)不重叠地放在一个底面为长方形(长为
,宽为
)的盒子底部,如图
,盒子底面未被卡片覆盖的部分用阴影表示.求图
中两块阴影部分的周长和.
22.
(8分)不改变多项式的值,按下列要求,给多项式
添括号:
(1)把多项式后三项括起来,括号前面是“”号;
(2)把多项式的前两项括起来,括号前面是“”号;
(3)把多项式后三项括起来,括号前面是“”号;
(4)把多项式中间的两项括起来,括号前面是“”号.
23.
(8分)解方程:.
24.
(10分)已知当
时,多项式
的值为
.
(1)求
的值.
(2)若当
时,该多项式的值为
.
①当
时,求该多项式的值;
②若
,,,试比较
与
的大小,并说明理由.
25.
(10分)池塘边有一块长为
米,宽为
米的长方形土地,如图,现将其中三面留出宽都是
米的小路,中间余下的长方形部分为菜地.用代数式表示:
(1)菜地的长为
米,宽为
米;
(2)菜地的面积为多少平方米
答案
第一部分
1.
D
2.
C
【解析】
的分母中含有未知数,不是整式,其余的都是整式,有
个.
3.
C
4.
C
5.
D
6.
D
7.
C
8.
D
9.
D
10.
C
【解析】因为学校租用
座的客车
辆,则余下
人无座位,所以师生的总人数为
.又因为租用
座的客车则可少租用
辆,所以乘坐最后一辆
座客车的人数为
.
11.
B
【解析】由已知得,,,,,
,
,,,,
则
.
12.
D
【解析】
,,,
,,.
第二部分
13.
单项式与多项式
14.
,
15.
,,,
16.
【解析】
17.
【解析】
一列数为
,,,,,,,
这列数的第
个数可以表示为
,
其中某三个相邻数的积是
,
设这三个相邻的数分别为
,,,
则
,
,
,解得
,
这三个相邻的数分别为
,,,
这三个数的和是
18.
【解析】依题意,空格中的一项是
第三部分
19.
单项式:,,,,.
20.
.
21.
.
22.
(1)
.
(2)
.
(3)
.
(4)
.
23.
去括号,得
移项,得
合并同类项,得
系数化为
,得
24.
(1)
把
代入
,得
.
(2)
①把
代入
,得
.
所以
.
把
代入
,得
.
②
,理由如下:
因为
,
所以
,
同号.
由①知
,
所以
,.
因为
,
所以
.
因为
,且
,
所以
.
所以
.
所以
.
25.
(1)
;
(2)
由()可得菜地的面积为
平方米.
米
厘米,
覆盖
个整数点.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
