山东省泰安市新泰市2020-2021学年七年级下学期期末数学试题(Word版 含答案)
文档属性
| 名称 | 山东省泰安市新泰市2020-2021学年七年级下学期期末数学试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-02 07:47:48 | ||
图片预览


文档简介
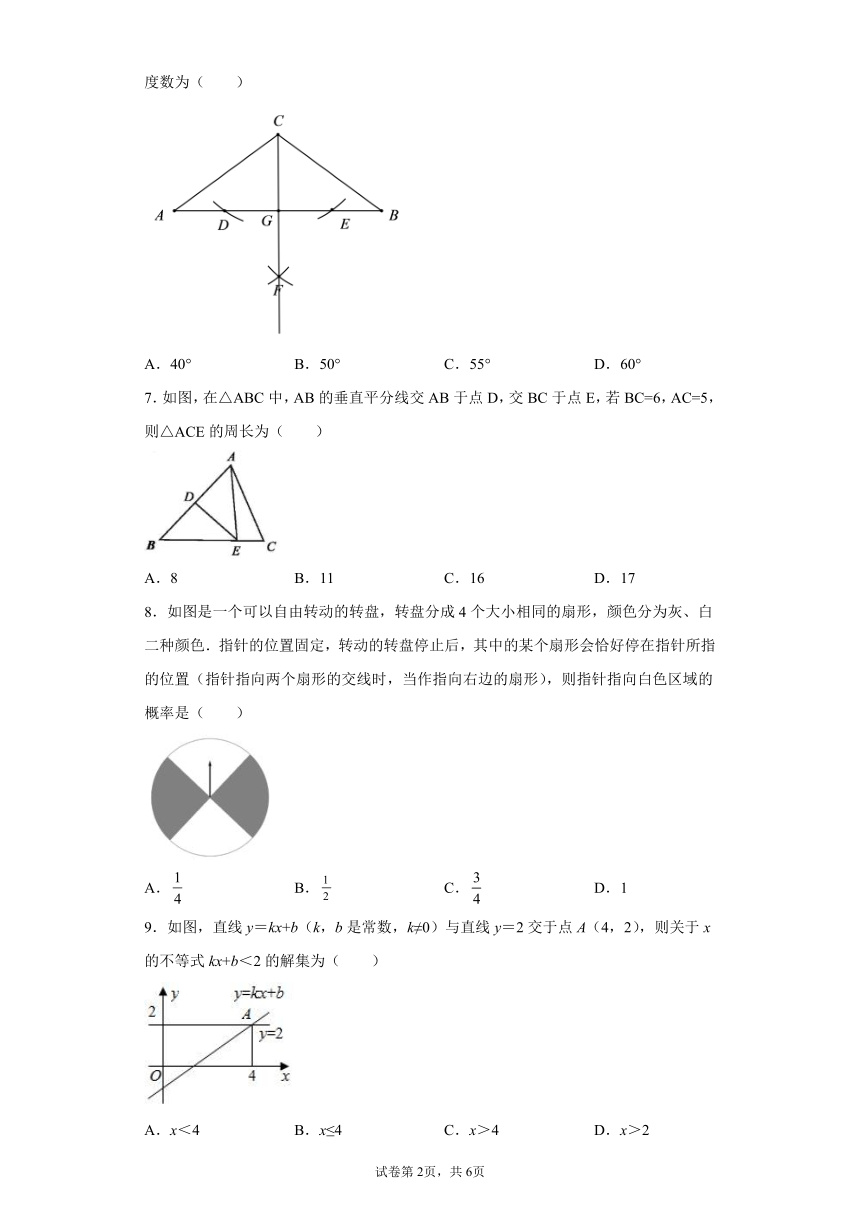
山东省泰安市新泰市2020-2021学年七年级下学期期末数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各组数值中,是二元一次方程的一个解的是(
)
A.
B.
C.
D.
2.如图,给出下列条件:①;②;③且
;④且;其中能推出
的有(
)
A.1
B.2
C.3
D.4
3.不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是(
)
A.3个球都是黑球
B.3个球都是白球
C.三个球中有黑球
D.3个球中有白球
4.如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为(
)
A.70°
B.80°
C.90°
D.100°
5.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
6.如图,在中,,,观察图中尺规作图的痕迹,可知的度数为(
)
A.40°
B.50°
C.55°
D.60°
7.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为(
)
A.8
B.11
C.16
D.17
8.如图是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,颜色分为灰、白二种颜色.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向白色区域的概率是(
)
A.
B.
C.
D.1
9.如图,直线y=kx+b(k,b是常数,k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为( )
A.x<4
B.x≤4
C.x>4
D.x>2
10.《九章算术》中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现有30钱,买得2斗酒.问醇酒、行酒各买得多少?设醇酒买得x斗,行酒买得y斗,则可列二元一次方程组为(
)
A.
B.
C.
D.
11.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有(
)
A.1个
B.2个
C.3个
D.4个
12.如图,直线分别与直线、相交于点E、F,与
互补,的平分线与的平分线交于点P,与直线交于点
G,交于点H,则下列说法:①;②
;③;④;⑤
.其中正确的有(
)个
A.2
B.3
C.4
D.5
二、填空题
13.不等式的解集是______.
14.某厂的甲、乙两个小组共同生产某种产品.若甲组先生产1天,然后两组又一起生产了5天,则两组产量一样多.若甲组先生产了300个产品,然后两组同时生产4天,则乙组比甲组多生产100个产品.若甲乙两组同时生产,则一天共生产___________个产品.
15.在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.己知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为__________.
16.若关于x的不等式组有且只有3个整数解,则a的取值范围是
________.
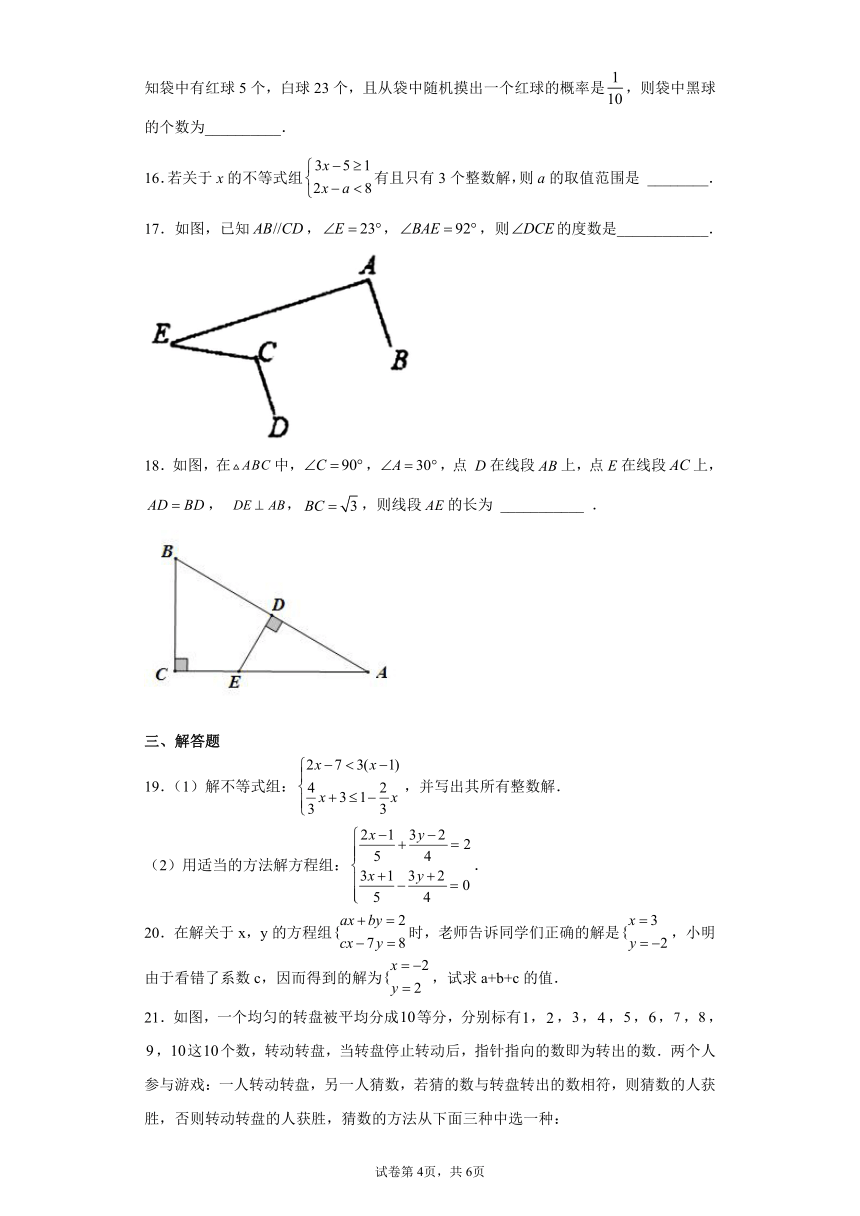
17.如图,已知,,,则的度数是____________.
18.如图,在中,,,点
D在线段上,点E在线段上,,
,,则线段的长为
___________
.
三、解答题
19.(1)解不等式组:,并写出其所有整数解.
(2)用适当的方法解方程组:.
20.在解关于x,y的方程组时,老师告诉同学们正确的解是,小明由于看错了系数c,因而得到的解为,试求a+b+c的值.
21.如图,一个均匀的转盘被平均分成等分,分别标有,,,,,,,,,这个数,转动转盘,当转盘停止转动后,指针指向的数即为转出的数.两个人参与游戏:一人转动转盘,另一人猜数,若猜的数与转盘转出的数相符,则猜数的人获胜,否则转动转盘的人获胜,猜数的方法从下面三种中选一种:
(1)猜“是奇数”或“是偶数”;
(2)猜“是的倍数”或“不是的倍数”;
(3)猜“是大于的数”或“不是大于的数”.
如果你是猜数的游戏者,为了尽可能获胜,你将选择哪种猜数方法?请说明理由.
22.如图,在中,,
E为边上的点,且,D为线段的中点,过点
E作,过点A作,且
,相交于点F.求证:
(1);
(2)若,求线段的长.
23.(1)已知:如图1,.求证:
(2)如图2,已知,在的平分线上取两个点M、N,使得,求证:.
24.快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元;两种机器人的单价与每小时分拣快递的数量如下表:
甲型机器人
乙型机器人
购买单价(万元/台)
m
n
每小时拣快递数量(件)
1200
1000
(1)求购买甲、乙两种型号的机器人所需的单价m和n分别为多少万元/台?
(2)若该公司计划购买这两种型号的机器人共8台,购买甲型机器人不超过4台,并且使这8台机器人每小时分拣快递件数总和不少于8400件,则该公司有几种购买方案?哪种方案费用最低,最低费用是多少万元?
25.如图,在中,,,点D是上一动点,连接,过点A作,并且始终保持,连接.
(1)求证:;
(2)若平分交于F,若,,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
2.C
3.B
4.B
5.C
6.B
7.B
8.B
9.A
10.D
11.C
12.C
13.x<
14.1100
15.22
16.0<a≤2
17.115°
18.2
19.(1),整数解为-3,-2,-1;(2)
20.7
21.选择猜第二种
22.(1)略;(2)
23.(1)略;(2)略
24.(1)甲、乙两种型号的机器人每台价格分别是6万元、4万元;(2)公司有3种购买方案,分别是购买甲型机器人2台,乙型机器人6台,购买甲型机器人3台,乙型机器人5台,购买甲型机器人4台,乙型机器人4台;该公司购买甲型机器人2台,乙型机器人6台这个方案费用最低,最低费用是36万元
25.(1)略;(2)5
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各组数值中,是二元一次方程的一个解的是(
)
A.
B.
C.
D.
2.如图,给出下列条件:①;②;③且
;④且;其中能推出
的有(
)
A.1
B.2
C.3
D.4
3.不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是(
)
A.3个球都是黑球
B.3个球都是白球
C.三个球中有黑球
D.3个球中有白球
4.如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为(
)
A.70°
B.80°
C.90°
D.100°
5.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
6.如图,在中,,,观察图中尺规作图的痕迹,可知的度数为(
)
A.40°
B.50°
C.55°
D.60°
7.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为(
)
A.8
B.11
C.16
D.17
8.如图是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,颜色分为灰、白二种颜色.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向白色区域的概率是(
)
A.
B.
C.
D.1
9.如图,直线y=kx+b(k,b是常数,k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为( )
A.x<4
B.x≤4
C.x>4
D.x>2
10.《九章算术》中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现有30钱,买得2斗酒.问醇酒、行酒各买得多少?设醇酒买得x斗,行酒买得y斗,则可列二元一次方程组为(
)
A.
B.
C.
D.
11.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有(
)
A.1个
B.2个
C.3个
D.4个
12.如图,直线分别与直线、相交于点E、F,与
互补,的平分线与的平分线交于点P,与直线交于点
G,交于点H,则下列说法:①;②
;③;④;⑤
.其中正确的有(
)个
A.2
B.3
C.4
D.5
二、填空题
13.不等式的解集是______.
14.某厂的甲、乙两个小组共同生产某种产品.若甲组先生产1天,然后两组又一起生产了5天,则两组产量一样多.若甲组先生产了300个产品,然后两组同时生产4天,则乙组比甲组多生产100个产品.若甲乙两组同时生产,则一天共生产___________个产品.
15.在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.己知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为__________.
16.若关于x的不等式组有且只有3个整数解,则a的取值范围是
________.
17.如图,已知,,,则的度数是____________.
18.如图,在中,,,点
D在线段上,点E在线段上,,
,,则线段的长为
___________
.
三、解答题
19.(1)解不等式组:,并写出其所有整数解.
(2)用适当的方法解方程组:.
20.在解关于x,y的方程组时,老师告诉同学们正确的解是,小明由于看错了系数c,因而得到的解为,试求a+b+c的值.
21.如图,一个均匀的转盘被平均分成等分,分别标有,,,,,,,,,这个数,转动转盘,当转盘停止转动后,指针指向的数即为转出的数.两个人参与游戏:一人转动转盘,另一人猜数,若猜的数与转盘转出的数相符,则猜数的人获胜,否则转动转盘的人获胜,猜数的方法从下面三种中选一种:
(1)猜“是奇数”或“是偶数”;
(2)猜“是的倍数”或“不是的倍数”;
(3)猜“是大于的数”或“不是大于的数”.
如果你是猜数的游戏者,为了尽可能获胜,你将选择哪种猜数方法?请说明理由.
22.如图,在中,,
E为边上的点,且,D为线段的中点,过点
E作,过点A作,且
,相交于点F.求证:
(1);
(2)若,求线段的长.
23.(1)已知:如图1,.求证:
(2)如图2,已知,在的平分线上取两个点M、N,使得,求证:.
24.快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元;两种机器人的单价与每小时分拣快递的数量如下表:
甲型机器人
乙型机器人
购买单价(万元/台)
m
n
每小时拣快递数量(件)
1200
1000
(1)求购买甲、乙两种型号的机器人所需的单价m和n分别为多少万元/台?
(2)若该公司计划购买这两种型号的机器人共8台,购买甲型机器人不超过4台,并且使这8台机器人每小时分拣快递件数总和不少于8400件,则该公司有几种购买方案?哪种方案费用最低,最低费用是多少万元?
25.如图,在中,,,点D是上一动点,连接,过点A作,并且始终保持,连接.
(1)求证:;
(2)若平分交于F,若,,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
2.C
3.B
4.B
5.C
6.B
7.B
8.B
9.A
10.D
11.C
12.C
13.x<
14.1100
15.22
16.0<a≤2
17.115°
18.2
19.(1),整数解为-3,-2,-1;(2)
20.7
21.选择猜第二种
22.(1)略;(2)
23.(1)略;(2)略
24.(1)甲、乙两种型号的机器人每台价格分别是6万元、4万元;(2)公司有3种购买方案,分别是购买甲型机器人2台,乙型机器人6台,购买甲型机器人3台,乙型机器人5台,购买甲型机器人4台,乙型机器人4台;该公司购买甲型机器人2台,乙型机器人6台这个方案费用最低,最低费用是36万元
25.(1)略;(2)5
答案第1页,共2页
答案第1页,共2页
同课章节目录
