5.7 三角函数的应用 课时必刷练习(含解析)——2021-2022学年高一数学上学期人教A版(2019)必修第一册
文档属性
| 名称 | 5.7 三角函数的应用 课时必刷练习(含解析)——2021-2022学年高一数学上学期人教A版(2019)必修第一册 |  | |
| 格式 | docx | ||
| 文件大小 | 917.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 11:45:29 | ||
图片预览


文档简介
第5.7课时
三角函数的应用
一、单选题(本大题共8小题,每小题只有一个选项符合题意)
1.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定的解析式为
A.
B.
C.
D.
2.位于潍坊滨海的“滨海之眼”摩天轮是世界上最高的无轴摩天轮,该摩天轮的直径均为124米,中间没有任何支撑,摩天轮顺时针匀速旋转一圈需要30分钟,当乘客乘坐摩天轮到达最高点时,距离地面145米,可以俯瞰白浪河全景,图中与地面垂直,垂足为点,某乘客从处进入处的观景舱,顺时针转动分钟后,第1次到达点,此时点与地面的距离为114米,则
A.16分钟
B.18分钟
C.20分钟
D.22分钟
3.设函数,将的图象向右平移个单位后,所得的函数为偶函数,则的值可以是
A.1
B.
C.2
D.
4.如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,是锐角,大小为β.图中阴影区域的面积的最大值为
A.4β+4cosβ
B.4β+4sinβ
C.2β+2cosβ
D.2β+2sinβ
5.函数的最小正周期为π,若其图象向左平移个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点对称
B.关于点对称
C.关于直线对称
D.关于直线对称
6.一根长的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移与时间的函数关系式是,其中是重力加速度,当小球摆动的周期是时,线长等于
A.
B.
C.
D.
7.函数其中的图象如图所示,为了得到图象,则只需将的图象
A.向右平移个长度单位
B.向左平移个长度单位
C.向右平移个长度单位
D.向左平移个长度单位
8.在地面上同一地点观测远方匀速垂直上升的热气球,在上午10点整热气球的仰角是,到上午10点20分的仰角变成.请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数
0.5
0.559
0.629
0.643
0.656
0.669
0.682
0.695
0.707
0.866
0.829
0.777
0.766
0.755
0.743
0.731
0.719
0.707
0.577
0.675
0.810
0.839
0.869
0.900
0.933
0.966
1.0
A.
B.
C.
D.
二、多选题(本大题共4小题,每小题有两项或以上符合题意)
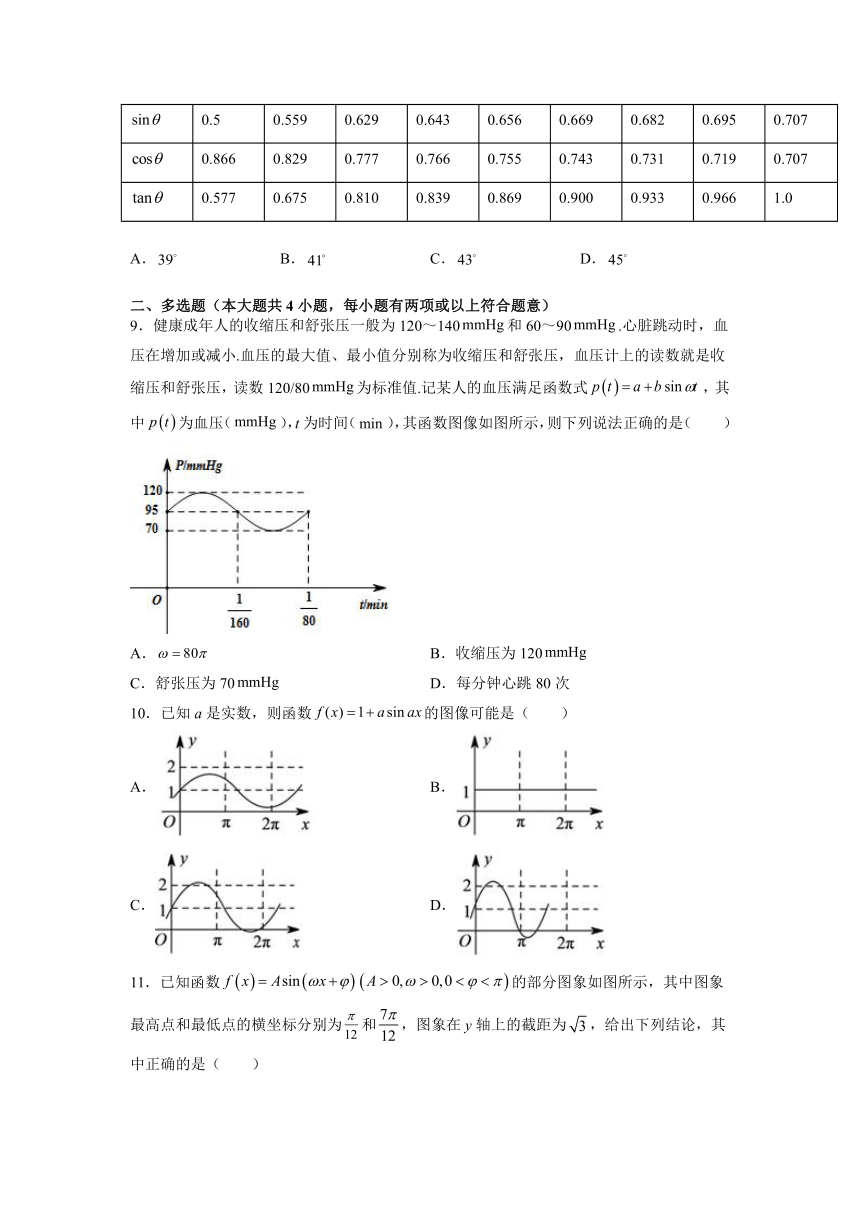
9.健康成年人的收缩压和舒张压一般为120~140和60~90.心脏跳动时,血压在增加或减小.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80为标准值.记某人的血压满足函数式,其中为血压(),t为时间(),其函数图像如图所示,则下列说法正确的是(
)
A.
B.收缩压为120
C.舒张压为70
D.每分钟心跳80次
10.已知a是实数,则函数的图像可能是(
)
A.
B.
C.
D.
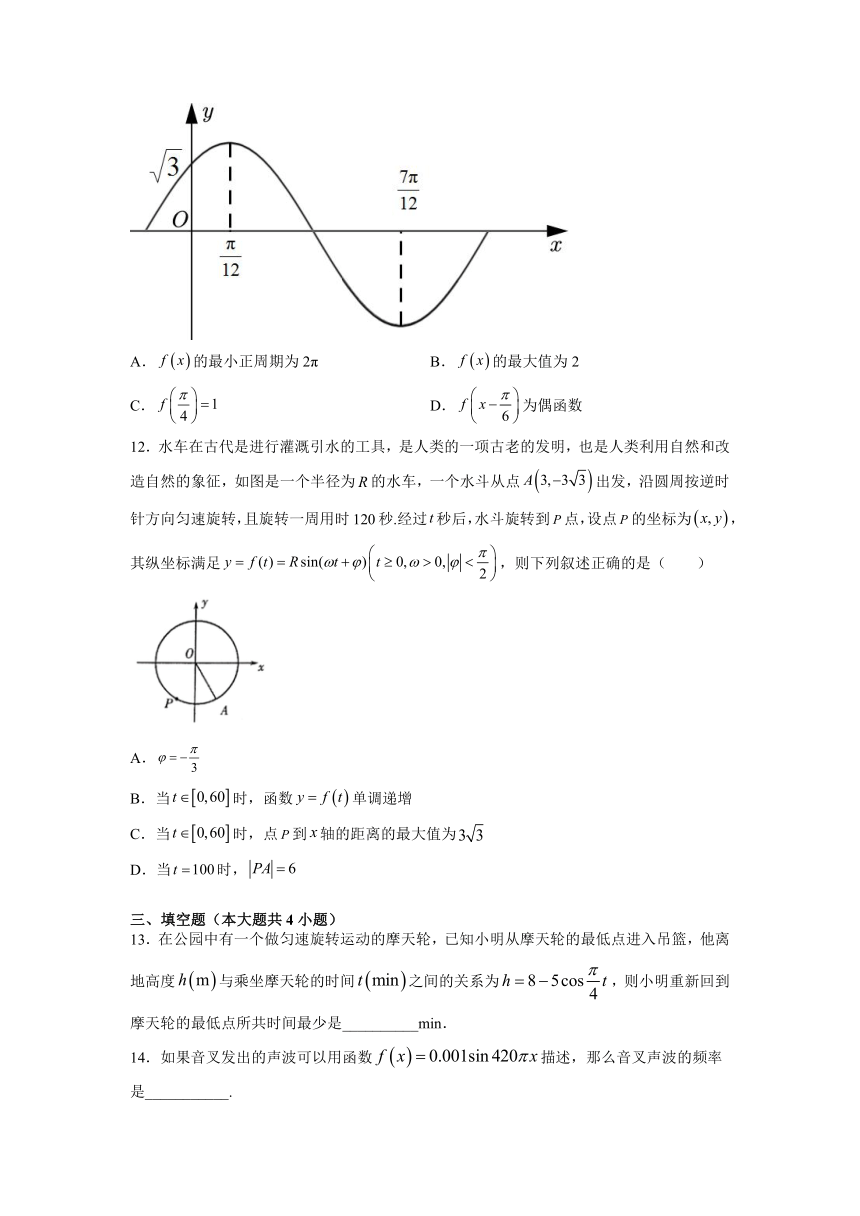
11.已知函数的部分图象如图所示,其中图象最高点和最低点的横坐标分别为和,图象在y轴上的截距为,给出下列结论,其中正确的是(
)
A.的最小正周期为2π
B.的最大值为2
C.
D.为偶函数
12.水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时120秒.经过秒后,水斗旋转到点,设点的坐标为,其纵坐标满足,则下列叙述正确的是(
)
A.
B.当时,函数单调递增
C.当时,点到轴的距离的最大值为
D.当时,
三、填空题(本大题共4小题)
13.在公园中有一个做匀速旋转运动的摩天轮,已知小明从摩天轮的最低点进入吊篮,他离地高度与乘坐摩天轮的时间之间的关系为,则小明重新回到摩天轮的最低点所共时间最少是__________min.
14.如果音叉发出的声波可以用函数描述,那么音叉声波的频率是___________.
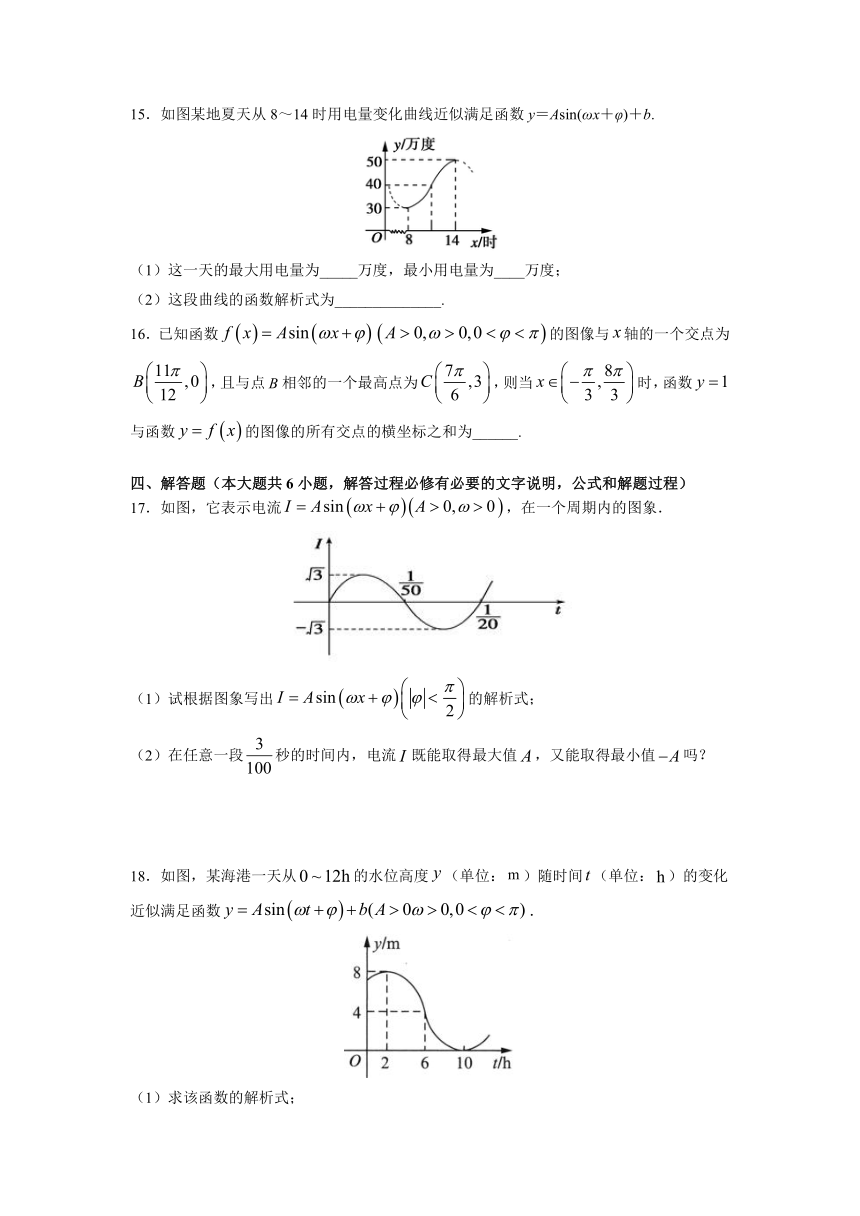
15.如图某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)这一天的最大用电量为_____万度,最小用电量为____万度;
(2)这段曲线的函数解析式为______________.
16.已知函数的图像与轴的一个交点为,且与点相邻的一个最高点为,则当时,函数与函数的图像的所有交点的横坐标之和为______.
四、解答题(本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程)
17.如图,它表示电流,在一个周期内的图象.
(1)试根据图象写出的解析式;
(2)在任意一段秒的时间内,电流既能取得最大值,又能取得最小值吗?
18.如图,某海港一天从的水位高度(单位:)随时间(单位:)的变化近似满足函数.
(1)求该函数的解析式;
(2)若该海港在水位高度不低于时为轮船最佳进港时间,那么该海港在,轮船最佳进港时间总共多少小时?
19.一个大风车的半径为8米,风车按逆时针方向匀速旋转,并且12分钟旋转一周,它的最低点离地面2米,设风车开始旋转时其翼片的一个端点在风车的最低点,求:
(1)点离地面距离(米与时间(分钟)之间的函数关系式;
(2)在第一圈的什么时间段点离地面的高度超过14米?
20.一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点从水中浮现时(图中点P0)开始计算时间.
(1)试建立适当的坐标系,将点P距离水面的高度(m)表示为时间(s)的函数;
(2)点第一次到达最高点大约要多长时间?
(3)记,求证:不论为何值,是定值.
21.如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
(1)将图书馆底面矩形ABCD的面积S表示成θ的函数.
(2)若R=45
m,求当θ为何值时,矩形ABCD的面积S最大?最大面积是多少?(取=1.414)
22.如图,直角坐标系建立在湖泊的某一恰当位置,现准备在湖泊的一侧修建一条观光大道,它的前一段是以为圆心,为半径的圆弧,后一段是函数,时的图像,图像的最高点为.
(1)求函数的解析式;
(2)若在湖泊内修建如图的矩形水上乐园,其中折线为水上赛艇线路,问点落在圆弧上何处时赛艇线路最长?
参考答案
1.A
【解析】因为3月份达到最高价9千元,7月份价格最低为5千元,所以半周期,
故,所以,
又,所以
,
所以,
当时,,,.
,故选A.
2.C
【解析】根据题意,作,,如下图所示:
直径为,则,
所以
则
所以
,即
所以
因为摩天轮顺时针匀速旋转一圈需要30分钟
所以从A到B所需时间为分钟
所以选C
3.D
【解析】解:将函数f(x)=2sin(ωx)的图象向右平移个单位后,
可得y=2sin(ωx)的图象.
∵所得的函数为偶函数,∴kπ,k∈Z.
令k=﹣1,可得ω,
故选D.
4.B
【解析】观察图象可知,当P为弧AB的中点时,阴影部分的面积S取最大值,
此时∠BOP=∠AOP=π-β,
面积S的最大值为+S△POB+
S△POA=4β+
.
故选B.
5.C
【解析】因为函数的最小正周期为π,所以,图象向左平移个单位后得到,由得到的函数是奇函数可得,即.令得,,故A,B均不正确;令得,,时可得C正确.故选C.
6.D
【解析】由题意,可知函数的关系式是,
所以函数的最小正周期为,∴,
所以线长为,故选D.
7.D
【解析】由题意,三角函数的图象可知,且,即
又由,解得,即,
又由,解得,
即,又由,所以,即,
又函数向左平移个长度单位,即可得到,故选D.
8.B
【解析】设十点时气球距离地面高度为h,10点20分,高度为h+m,11点时高度为H,此时的角度为,根据直角三角形的三角函数性质得到
,因为气球是匀速上升的,故H=h+3m,
由表格中的数据得到m=0.17h,H=1.51h,代入上述方程得到
根据表格中的数据得到数据最近接.
故答案为B.
9.BCD
【解析】由图知:,所以,可得,故选项A不正确;
所以,
由图知在一个周期内最大值为,最小值为,所以收缩压为120,舒张压为70,故选项B、C正确;
每分钟心跳数为频率,故选项D正确,
故选:BCD.
10.ABD
【解析】时,,图象为,
若,则,此时.
因此不妨设,,则,,图象可能为D,
若,则,,图象可能为A.
故选:ABD.
11.BC
【解析】根据函数的部分图象,可得,求得,
再根据五点法作图可得,求得,
再根据图象经过点,可得,∴,
∴,
故的最小正周期为π,故A错误;
显然,的最大值为2,故B正确;
,故C正确;
,为奇函数,故D错误.
故选:BC
12.AD
【解析】由题意,R==6,T=120=,∴ω=,当t=0时,y=f(t)=,
代入可得=6sin
φ,∵,∴φ=-.故A正确;
所以,当时,,所以函数在不是单调递增的,故B不正确;
因为,,所以点P到x轴的距离的最大值为6,故C不正确;
当时,,此时,点,,故D正确,
故选:AD.
13.8
【解析】由题意,函数是一个周期函数,且周期为,
所以小明重新回到摩天轮的最低点所共时间最少一个周期,即.
故答案为:.
14.210
【解析】由题可得音叉声波的周期为,所以音叉声波的频率为.
故答案为:210.
15.50
30
【解析】由图知,最大用电量为50,最小用电量为30,
故,所以,
又由图象可得半周期为,,故,
又时,,∴
,∴.
故.
故答案:50,30,.
16.
【解析】由题意可得:
,则,
所以,
由一个最高点为,则,
,
代入可得:,
由,可得:,
,
如图:与函数的图像的共有6个交点,
分别关于,所有交点的横坐标之和为.
故答案为:.
17.(1);(2)不能.
【解析】(1)由题图知,,
∴,所以,
又是该函数图象的零点,
∴结合图形可得:,即,符合,
∴.
(2)不能.因为由(1)有,所以不可能.
18.(1),;(2).
【解析】(1)由图可知,,.
∵,∴,解得,
∴.
将,代入上式,解得,,
∵,∴,
故该曲线的函数解析式为,.
(2)由题意得,即,解得,,即,.
∵,∴当时,即,
∴该海港在的轮船最佳进港时间总共为.
19.(1),;(2).
【解析】(1)设,
由题意得:,,;
则,当时,,即;
因此,;
因此,,;
(2)由题意:,即:;
则:;
又因为,
所以.
20.(1)坐标系见解析,;(2)1s;(3)证明见解析.
【解析】(1)以水轮所在平面与水面的交线为x轴,以过点O且与水面垂直的直线为y轴,
建立如图所示的直角坐标系,
设,则,
因为,所以,所以,
当时,,即,所以,
因为,所以,所以.
(2)由(1)知,
令,可得,
所以,解得,
所以当时,点第一次到达最高点,
∴点第一次到达最高点大约要的时间.
(3)由(1)知,
,
所以(为定值).
21.(1)S=R2sin-R2,θ∈;(2)当θ=时,矩形ABCD的面积S最大,最大面积为838.35
m2.
【解析】解:(1)由题意,可知点M为PQ的中点,所以OM⊥AD.
设OM与BC的交点为F,则BC=2Rsin
θ,OF=Rcos
θ,所以AB=OF-AD=Rcos
θ-Rsin
θ.
所以S=AB·BC=2Rsin
θ(Rcos
θ-Rsin
θ)=R2(2sin
θcos
θ-2sin2θ)=R2(sin
2θ-1+cos
2θ)=R2sin-R2,θ∈.
(2)因为θ∈,所以2θ+∈,
所以当2θ+,即θ=时,S有最大值.
Smax=(-1)R2=(-1)×452=0.414×2
025=838.35(m2).
故当θ=时,矩形ABCD的面积S最大,最大面积为838.35
m2.
22.(1),;(2)当点坐标为时赛艇线路最长.
【解析】(1)由图象知,,即,则,
将代入,则,
则,又,,
所以,;
(2)在中令,得,∴.
连接,设,,则.
设赛艇线路长为,则,
当时,有最大值,此时.
所以当点坐标为时赛艇线路最长.
三角函数的应用
一、单选题(本大题共8小题,每小题只有一个选项符合题意)
1.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定的解析式为
A.
B.
C.
D.
2.位于潍坊滨海的“滨海之眼”摩天轮是世界上最高的无轴摩天轮,该摩天轮的直径均为124米,中间没有任何支撑,摩天轮顺时针匀速旋转一圈需要30分钟,当乘客乘坐摩天轮到达最高点时,距离地面145米,可以俯瞰白浪河全景,图中与地面垂直,垂足为点,某乘客从处进入处的观景舱,顺时针转动分钟后,第1次到达点,此时点与地面的距离为114米,则
A.16分钟
B.18分钟
C.20分钟
D.22分钟
3.设函数,将的图象向右平移个单位后,所得的函数为偶函数,则的值可以是
A.1
B.
C.2
D.
4.如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,是锐角,大小为β.图中阴影区域的面积的最大值为
A.4β+4cosβ
B.4β+4sinβ
C.2β+2cosβ
D.2β+2sinβ
5.函数的最小正周期为π,若其图象向左平移个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点对称
B.关于点对称
C.关于直线对称
D.关于直线对称
6.一根长的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移与时间的函数关系式是,其中是重力加速度,当小球摆动的周期是时,线长等于
A.
B.
C.
D.
7.函数其中的图象如图所示,为了得到图象,则只需将的图象
A.向右平移个长度单位
B.向左平移个长度单位
C.向右平移个长度单位
D.向左平移个长度单位
8.在地面上同一地点观测远方匀速垂直上升的热气球,在上午10点整热气球的仰角是,到上午10点20分的仰角变成.请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数
0.5
0.559
0.629
0.643
0.656
0.669
0.682
0.695
0.707
0.866
0.829
0.777
0.766
0.755
0.743
0.731
0.719
0.707
0.577
0.675
0.810
0.839
0.869
0.900
0.933
0.966
1.0
A.
B.
C.
D.
二、多选题(本大题共4小题,每小题有两项或以上符合题意)
9.健康成年人的收缩压和舒张压一般为120~140和60~90.心脏跳动时,血压在增加或减小.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80为标准值.记某人的血压满足函数式,其中为血压(),t为时间(),其函数图像如图所示,则下列说法正确的是(
)
A.
B.收缩压为120
C.舒张压为70
D.每分钟心跳80次
10.已知a是实数,则函数的图像可能是(
)
A.
B.
C.
D.
11.已知函数的部分图象如图所示,其中图象最高点和最低点的横坐标分别为和,图象在y轴上的截距为,给出下列结论,其中正确的是(
)
A.的最小正周期为2π
B.的最大值为2
C.
D.为偶函数
12.水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时120秒.经过秒后,水斗旋转到点,设点的坐标为,其纵坐标满足,则下列叙述正确的是(
)
A.
B.当时,函数单调递增
C.当时,点到轴的距离的最大值为
D.当时,
三、填空题(本大题共4小题)
13.在公园中有一个做匀速旋转运动的摩天轮,已知小明从摩天轮的最低点进入吊篮,他离地高度与乘坐摩天轮的时间之间的关系为,则小明重新回到摩天轮的最低点所共时间最少是__________min.
14.如果音叉发出的声波可以用函数描述,那么音叉声波的频率是___________.
15.如图某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)这一天的最大用电量为_____万度,最小用电量为____万度;
(2)这段曲线的函数解析式为______________.
16.已知函数的图像与轴的一个交点为,且与点相邻的一个最高点为,则当时,函数与函数的图像的所有交点的横坐标之和为______.
四、解答题(本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程)
17.如图,它表示电流,在一个周期内的图象.
(1)试根据图象写出的解析式;
(2)在任意一段秒的时间内,电流既能取得最大值,又能取得最小值吗?
18.如图,某海港一天从的水位高度(单位:)随时间(单位:)的变化近似满足函数.
(1)求该函数的解析式;
(2)若该海港在水位高度不低于时为轮船最佳进港时间,那么该海港在,轮船最佳进港时间总共多少小时?
19.一个大风车的半径为8米,风车按逆时针方向匀速旋转,并且12分钟旋转一周,它的最低点离地面2米,设风车开始旋转时其翼片的一个端点在风车的最低点,求:
(1)点离地面距离(米与时间(分钟)之间的函数关系式;
(2)在第一圈的什么时间段点离地面的高度超过14米?
20.一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点从水中浮现时(图中点P0)开始计算时间.
(1)试建立适当的坐标系,将点P距离水面的高度(m)表示为时间(s)的函数;
(2)点第一次到达最高点大约要多长时间?
(3)记,求证:不论为何值,是定值.
21.如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
(1)将图书馆底面矩形ABCD的面积S表示成θ的函数.
(2)若R=45
m,求当θ为何值时,矩形ABCD的面积S最大?最大面积是多少?(取=1.414)
22.如图,直角坐标系建立在湖泊的某一恰当位置,现准备在湖泊的一侧修建一条观光大道,它的前一段是以为圆心,为半径的圆弧,后一段是函数,时的图像,图像的最高点为.
(1)求函数的解析式;
(2)若在湖泊内修建如图的矩形水上乐园,其中折线为水上赛艇线路,问点落在圆弧上何处时赛艇线路最长?
参考答案
1.A
【解析】因为3月份达到最高价9千元,7月份价格最低为5千元,所以半周期,
故,所以,
又,所以
,
所以,
当时,,,.
,故选A.
2.C
【解析】根据题意,作,,如下图所示:
直径为,则,
所以
则
所以
,即
所以
因为摩天轮顺时针匀速旋转一圈需要30分钟
所以从A到B所需时间为分钟
所以选C
3.D
【解析】解:将函数f(x)=2sin(ωx)的图象向右平移个单位后,
可得y=2sin(ωx)的图象.
∵所得的函数为偶函数,∴kπ,k∈Z.
令k=﹣1,可得ω,
故选D.
4.B
【解析】观察图象可知,当P为弧AB的中点时,阴影部分的面积S取最大值,
此时∠BOP=∠AOP=π-β,
面积S的最大值为+S△POB+
S△POA=4β+
.
故选B.
5.C
【解析】因为函数的最小正周期为π,所以,图象向左平移个单位后得到,由得到的函数是奇函数可得,即.令得,,故A,B均不正确;令得,,时可得C正确.故选C.
6.D
【解析】由题意,可知函数的关系式是,
所以函数的最小正周期为,∴,
所以线长为,故选D.
7.D
【解析】由题意,三角函数的图象可知,且,即
又由,解得,即,
又由,解得,
即,又由,所以,即,
又函数向左平移个长度单位,即可得到,故选D.
8.B
【解析】设十点时气球距离地面高度为h,10点20分,高度为h+m,11点时高度为H,此时的角度为,根据直角三角形的三角函数性质得到
,因为气球是匀速上升的,故H=h+3m,
由表格中的数据得到m=0.17h,H=1.51h,代入上述方程得到
根据表格中的数据得到数据最近接.
故答案为B.
9.BCD
【解析】由图知:,所以,可得,故选项A不正确;
所以,
由图知在一个周期内最大值为,最小值为,所以收缩压为120,舒张压为70,故选项B、C正确;
每分钟心跳数为频率,故选项D正确,
故选:BCD.
10.ABD
【解析】时,,图象为,
若,则,此时.
因此不妨设,,则,,图象可能为D,
若,则,,图象可能为A.
故选:ABD.
11.BC
【解析】根据函数的部分图象,可得,求得,
再根据五点法作图可得,求得,
再根据图象经过点,可得,∴,
∴,
故的最小正周期为π,故A错误;
显然,的最大值为2,故B正确;
,故C正确;
,为奇函数,故D错误.
故选:BC
12.AD
【解析】由题意,R==6,T=120=,∴ω=,当t=0时,y=f(t)=,
代入可得=6sin
φ,∵,∴φ=-.故A正确;
所以,当时,,所以函数在不是单调递增的,故B不正确;
因为,,所以点P到x轴的距离的最大值为6,故C不正确;
当时,,此时,点,,故D正确,
故选:AD.
13.8
【解析】由题意,函数是一个周期函数,且周期为,
所以小明重新回到摩天轮的最低点所共时间最少一个周期,即.
故答案为:.
14.210
【解析】由题可得音叉声波的周期为,所以音叉声波的频率为.
故答案为:210.
15.50
30
【解析】由图知,最大用电量为50,最小用电量为30,
故,所以,
又由图象可得半周期为,,故,
又时,,∴
,∴.
故.
故答案:50,30,.
16.
【解析】由题意可得:
,则,
所以,
由一个最高点为,则,
,
代入可得:,
由,可得:,
,
如图:与函数的图像的共有6个交点,
分别关于,所有交点的横坐标之和为.
故答案为:.
17.(1);(2)不能.
【解析】(1)由题图知,,
∴,所以,
又是该函数图象的零点,
∴结合图形可得:,即,符合,
∴.
(2)不能.因为由(1)有,所以不可能.
18.(1),;(2).
【解析】(1)由图可知,,.
∵,∴,解得,
∴.
将,代入上式,解得,,
∵,∴,
故该曲线的函数解析式为,.
(2)由题意得,即,解得,,即,.
∵,∴当时,即,
∴该海港在的轮船最佳进港时间总共为.
19.(1),;(2).
【解析】(1)设,
由题意得:,,;
则,当时,,即;
因此,;
因此,,;
(2)由题意:,即:;
则:;
又因为,
所以.
20.(1)坐标系见解析,;(2)1s;(3)证明见解析.
【解析】(1)以水轮所在平面与水面的交线为x轴,以过点O且与水面垂直的直线为y轴,
建立如图所示的直角坐标系,
设,则,
因为,所以,所以,
当时,,即,所以,
因为,所以,所以.
(2)由(1)知,
令,可得,
所以,解得,
所以当时,点第一次到达最高点,
∴点第一次到达最高点大约要的时间.
(3)由(1)知,
,
所以(为定值).
21.(1)S=R2sin-R2,θ∈;(2)当θ=时,矩形ABCD的面积S最大,最大面积为838.35
m2.
【解析】解:(1)由题意,可知点M为PQ的中点,所以OM⊥AD.
设OM与BC的交点为F,则BC=2Rsin
θ,OF=Rcos
θ,所以AB=OF-AD=Rcos
θ-Rsin
θ.
所以S=AB·BC=2Rsin
θ(Rcos
θ-Rsin
θ)=R2(2sin
θcos
θ-2sin2θ)=R2(sin
2θ-1+cos
2θ)=R2sin-R2,θ∈.
(2)因为θ∈,所以2θ+∈,
所以当2θ+,即θ=时,S有最大值.
Smax=(-1)R2=(-1)×452=0.414×2
025=838.35(m2).
故当θ=时,矩形ABCD的面积S最大,最大面积为838.35
m2.
22.(1),;(2)当点坐标为时赛艇线路最长.
【解析】(1)由图象知,,即,则,
将代入,则,
则,又,,
所以,;
(2)在中令,得,∴.
连接,设,,则.
设赛艇线路长为,则,
当时,有最大值,此时.
所以当点坐标为时赛艇线路最长.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
