2.2圆的的对称性 同步能力达标训练 2021-2022学年苏科版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.2圆的的对称性 同步能力达标训练 2021-2022学年苏科版九年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 492.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 00:00:00 | ||
图片预览


文档简介
2021-2022学年苏科版九年级数学上册《2.2圆的对称性》同步能力达标训练(附答案)
一、选择题
1.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米
B.(4﹣)米
C.2米
D.(4+)米
2.往水平放置的半径为13cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=24cm,则水的最大深度为( )
A.5cm
B.8cm
C.10cm
D.12cm
3.下列说法正确的是( )
A.4的平方根是2
B.平分弦的直径垂直弦并平分弦所对的弧
C.一组数据中有且仅有一个众数
D.等弧所对的弦相等
4.如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A.m
B.m
C.5m
D.m
5.已知,如图,线段AB是⊙O的直径,弦CD⊥AB于点E.若AE=2,CD=6,则OB的长度为( )
A.
B.
C.
D.5
6.如图AB是⊙O的直径,弦CD⊥AB于点E,OC=2cm,CD=2cm,则AE长是( )
A.(+2)cm
B.2cm
C.cm
D.4cm
7.已知⊙O的直径CD=100cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=96cm,则AC的长为( )
A.36cm或64cm
B.60cm或80cm
C.80cm
D.60cm
8.如图,⊙O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP长的取值范围是( )
A.3≤OP≤5
B.4<OP<5
C.4≤OP≤5
D.3<OP<5
9.若弦AB,CD是⊙O的两条平行弦,⊙O的半径为13,AB=10,CD=24,则AB,CD之间的距离为( )
A.7
B.17
C.5或12
D.7或17
10.如图,半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10cm
B.16cm
C.24cm
D.26cm
11.如图,已知⊙O的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为( )
A.3
B.4
C.3
D.4
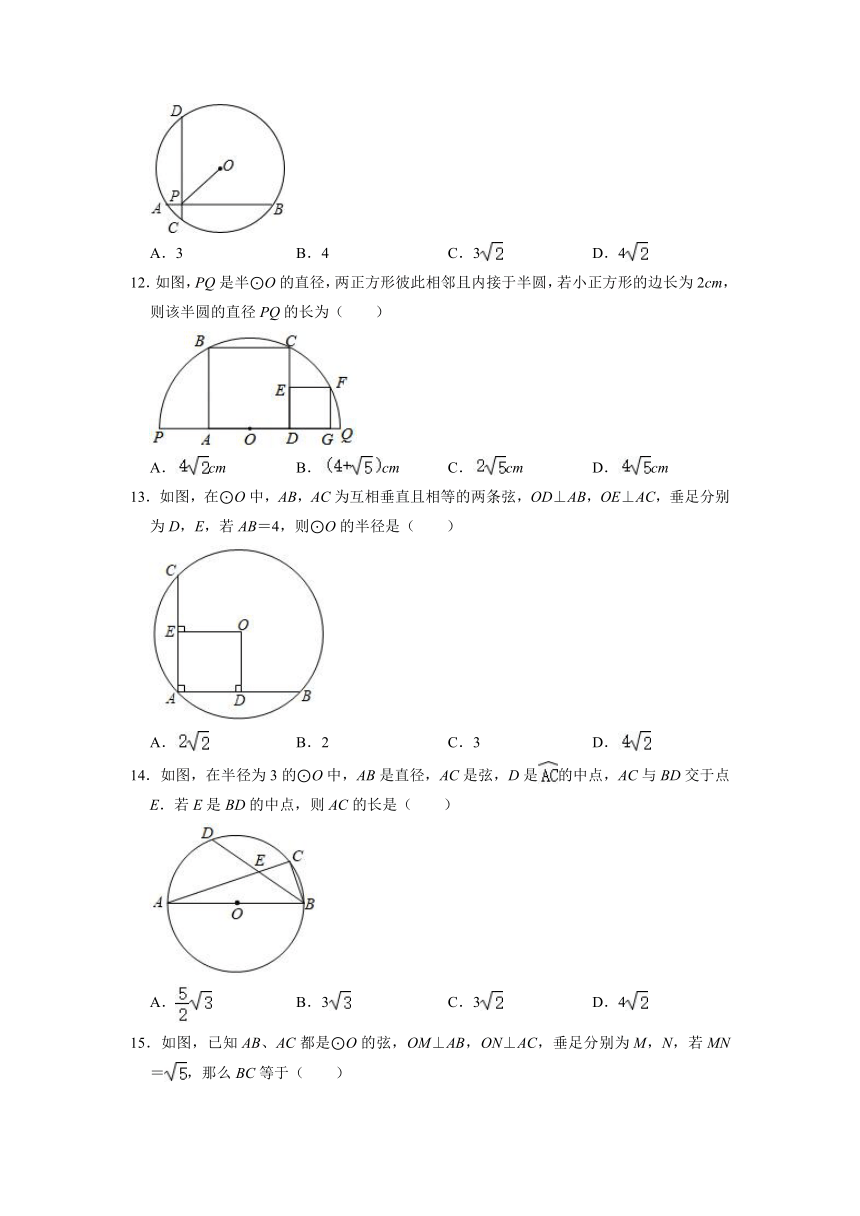
12.如图,PQ是半⊙O的直径,两正方形彼此相邻且内接于半圆,若小正方形的边长为2cm,则该半圆的直径PQ的长为( )
A.cm
B.cm
C.cm
D.cm
13.如图,在⊙O中,AB,AC为互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D,E,若AB=4,则⊙O的半径是( )
A.
B.2
C.3
D.
14.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
15.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,那么BC等于( )
A.5
B.
C.2
D.
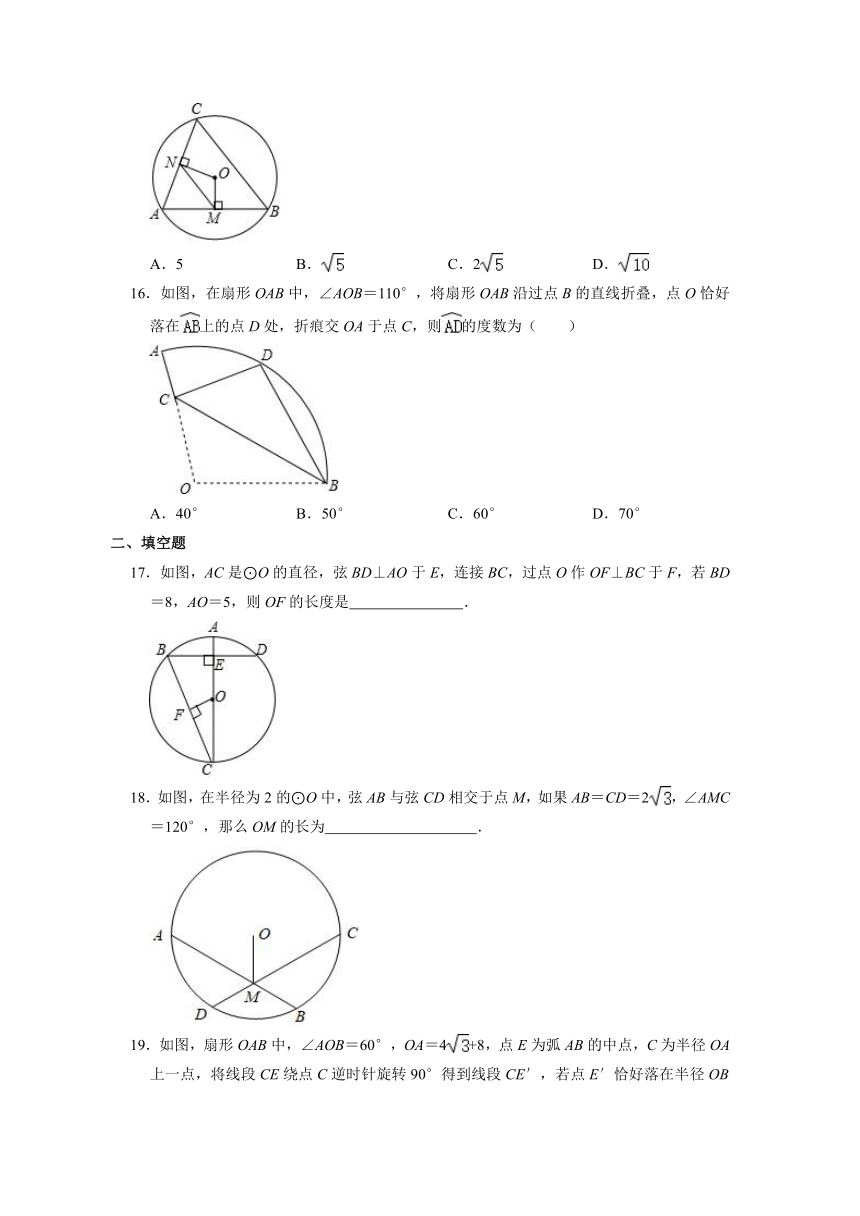
16.如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的度数为( )
A.40°
B.50°
C.60°
D.70°
二、填空题
17.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,AO=5,则OF的长度是
.
18.如图,在半径为2的⊙O中,弦AB与弦CD相交于点M,如果AB=CD=2,∠AMC=120°,那么OM的长为
.
19.如图,扇形OAB中,∠AOB=60°,OA=4+8,点E为弧AB的中点,C为半径OA上一点,将线段CE绕点C逆时针旋转90°得到线段CE′,若点E′恰好落在半径OB上,则OE′=
.
20.如图,AB,CD是⊙O的两条弦,若AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,OE与OF的关系是
(“相等”或“不等”).
三、解答题
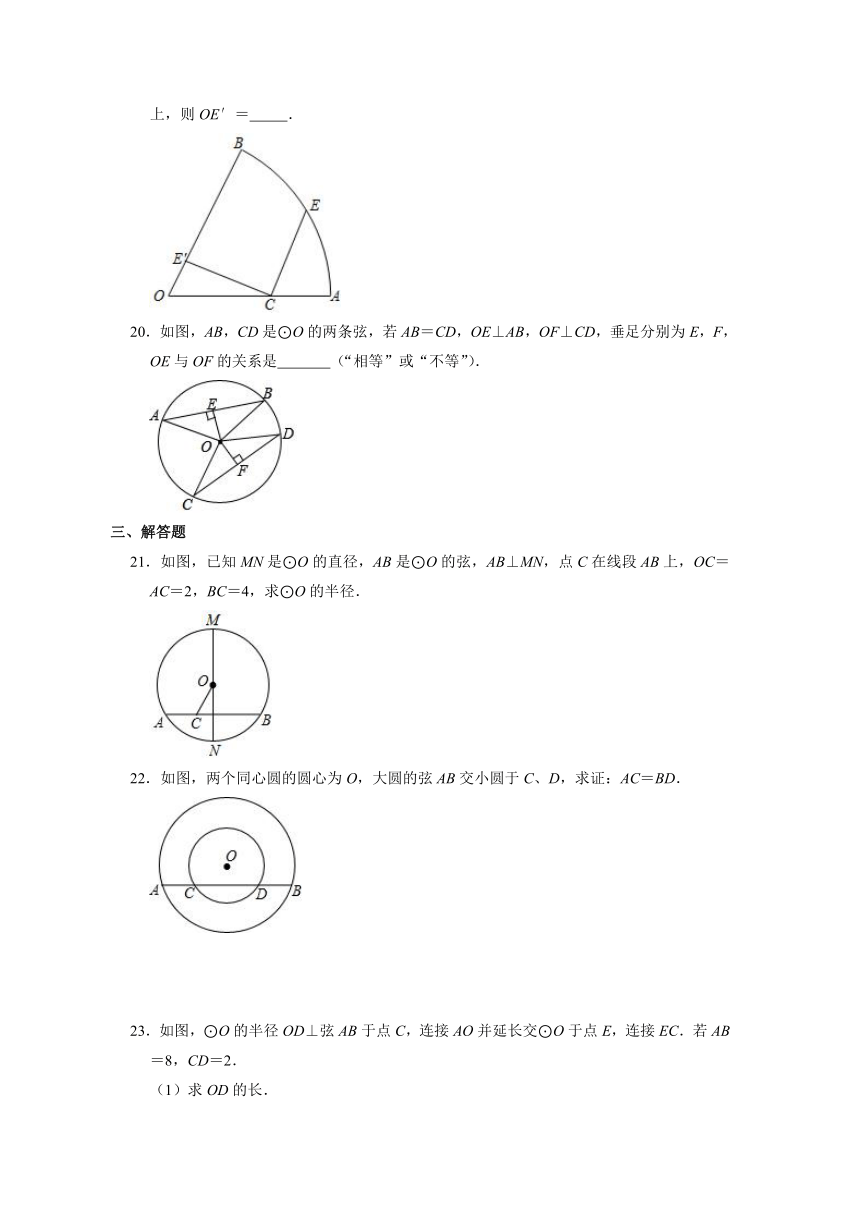
21.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
22.如图,两个同心圆的圆心为O,大圆的弦AB交小圆于C、D,求证:AC=BD.
23.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2.
(1)求OD的长.
(2)求EC的长.
24.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
25.已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且=.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
参考答案
1.解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
2.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:B.
3.解:A、4的平方根为±2,所以A选项的说法错误;
B、平分弦(非直径)的直径垂直弦并平分弦所对的弧,所以B选项的说法错误;
C、一组数据的众数可能有一个,也可能几个,所以C选项的说法错误;
D、等弧所对的弦相等,所以D选项的说法正确.
故选:D.
4.解:连接OB,如图所示:
由题意得:OC⊥AB,
∴AD=BD=AB=2(m),
在Rt△OBD中,根据勾股定理得:OD2+BD2=OB2,
即(OB﹣1)2+22=OB2,
解得:OB=(m),
即这个轮子的半径长为m,
故选:D.
5.解:连接OD,如图所示:
设⊙O的半径为R,
∵弦CD⊥AB于点E.CD=6,
∴DE=CE=CD=3,∠OED=90°,
在Rt△ODE中,由勾股定理得:DE2+OE2=OD2,
即32+(R﹣2)2=R2,
解得:R=,
即OB的长为,故选:B.
6.解:∵弦CD⊥AB于点E,CD=2cm,
∴CE=CD=(cm),
在Rt△OCE中,OC=2cm,
∴OE===(cm),
∴AE=OE+OA=(+2)cm,
故选:A.
7.解:连接AC,AO,
∵⊙O的直径CD=100cm,AB⊥CD,AB=96cm,
∴AM=AB=×96=48(cm),OD=OC=50(cm),
如图1,∵OA=50cm,AM=48cm,CD⊥AB,
∴OM===14(cm),
∴CM=OC+OM=50+14=64(cm),
∴AC===80(cm);
如图2,同理可得,OM=14cm,
∵OC=50cm,
∴MC=50﹣14=36(cm),
在Rt△AMC中,AC==60(cm);
综上所述,AC的长为80cm或60cm,
故选:B.
8.解:连接OA,过点O作OH⊥AB于H,
则AH=HB=AB=3,
由勾股定理得,OH==4,
当点P与点A(或点B)重合时,OP最大,当点P与点H重合时,OP最小,
∴线段OP长的取值范围是4≤OP≤5,
故选:C.
9.解:过O点作OE⊥AB于E,交CD于F,连接OA、OC,如图,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=AB=5,CF=DF=CD=12,
在Rt△OAE中,OE===12,
在Rt△OCF中,OF===5,
当圆心O在AB、CD之间,如图1,EF=OE+OF=12+5=17,
当圆心O不在AB、CD之间,如图2,EF=OE﹣OF=12﹣5=7,
综上所述,AB,CD之间的距离为7或17.
故选:D.
10.解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8cm,OD=13cm,
∴OC=5cm,
又∵OB=13cm,
∴Rt△BCO中,BC==12cm,
∴AB=2BC=24cm.
故选:C.
11.解:连接OB,作OE⊥AB于E,OF⊥CD于F,
则BE=AB=4,四边形PEOF为矩形,
∵AB=CD,OE⊥AB,OF⊥CD,
∴OE=OF,
∴矩形PEOF为正方形,
∴OE=PE,
在Rt△OEB中,OE==3,
∴OP==3,
故选:C.
12.解:如图,过O点作OH⊥BC于H,连接OC、OF,如图,
∵OH⊥BC,
∴BH=CH,
∵∠ODC=∠DCH=90°,
∴四边形ODCH为矩形,
∴CD=OH,OD=CH,
∴OH=2CH,
设OD=xcm,则OH=2xcm,OG=(2+x)cm,
在Rt△OCH中,OC==x(cm),
在Rt△OGF中,22+(2+x)2=(x)2,解得x1=2,x2=﹣1(舍去),
∴OC=2cm,
∴PQ=2OC=4cm.
故选:D.
13.解:∵OD⊥AB,
∴AD=BD=AB,
同理AE=CE=AC,
∵AB=AC=4,
∴AD=AE=2,
连接OA,
∵OD⊥AB,OE⊥AC,AB⊥AC,
∴∠OEA=∠BAC=∠ODA=90°,
∴四边形ADOE为矩形,
又∵AD=AE,
∴四边形ADOE为正方形,
∴OD=AD=2,
∴OA===2,
即⊙O的半径是2,
故选:A.
14.解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
15.解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AB与AC的中点,
∴MN是△ABC的中位线,
∴BC=2MN=2,
故选:C.
16.解:连接OD,如图,
∵扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,
∴BC垂直平分OD,
∴BD=BO,
∵OB=OD,
∴BD=BO=DO,
∴△OBD为等边三角形,
∴∠DOB=60°,
∴∠AOD=∠AOB﹣∠DOB=110°﹣60°=50°,
∴的度数为50°,
故选:B.
17.解:连接OB,
∵弦BD⊥AO,
∴BE=BD=4,
由勾股定理得,OE==3,
则CE=OC+OE=8,
∴BC==4,
∵OF⊥BC,
∴CF=BF=2,
∵∠CFO=∠CEB=90°,∠C=∠C,
∴OF=,
故答案为:.
18.解:如图,过点O作OE⊥AB,OF⊥CD,垂足为E、F,连接OA,
则AE=BE=AB=,CF=DF=CD=,
在Rt△AOE中,
∵OA=2,AE=,
∴OE==1,
∵AB=CD,
∴OE=OF=1,
又∵OM=OM,
∴Rt△OEM≌Rt△OFM(HL),
∴∠OME=∠OMF=∠AMC=60°,
∴OM=,
故答案为:.
19.解:过E点作EH⊥OA于H,过E′点作E′⊥OA于F,连接OE,如图,设OF=x,
∵∠AOB=60°,
∴OE′=2OF=2x,E′F=OF=x,
∵点E为弧AB的中点,
∴∠AOE=∠BOE=∠AOB=30°,
∴EH=OE=(4+8)=2+4,
OH=EH=6+4,
∵线段CE绕点C逆时针旋转90°得到线段CE′,
∴CE=CE′,∠ECE′=90°,
∵∠ECH+∠CEH=90°,∠ECH+∠E′CF=90°,
∴∠CEH=∠E′CF,
在△CEH和△E′CF中
,
∴△CEH≌△E′CF(AAS),
∴CH=E′F=x,CF=EH=2+4,
∵OH=OF+FC+CH,
∴x+2+4+x=6+4,解得x=2,
∴OE′=2x=4.
故答案为4.
20.解:∵OE⊥AB,OF⊥CD,
∴AE=EB,CF=DF,
∵AB=CD,
∴AE=CF,
∵OA=OC,∠AEO=∠CFO,AE=CF,
∴Rt△AEO≌Rt△CFO(HL),
∴OE=OF.
故答案为:相等.
21.解:连接OB,设AB与MN交于点D,如图所示:
∵AC=2,BC=4,
∴AB=AC+BC=6,
∵AB⊥MN,
∴AD=BD=AB=3,∠ODC=∠ODB=90°,
∴CD=AD﹣AC=1,
∴OD===,
∴OB===2,
即⊙O的半径为2.
22.证明:
过O作OE⊥AB于E,
则OE⊥CD,
∵OE过O,
∴由垂径定理得:AE=BE,CE=DE,
∴AE﹣CE=BE﹣DE,
即AC=BD.
23.解:(1)连接BE,
设⊙O半径为r,则OA=OD=r,OC=r﹣2,
∵OD⊥AB,
∴∠ACO=90°,
AC=BC=AB=4,
在Rt△ACO中,由勾股定理得:r2=42+(r﹣2)2,
r=5,
∴OD=r=5;
(2)由(1)得:AE=2r=10,
∵AE为⊙O的直径,
∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中,EC===2.
24.证明:∵AB=CD,
∴=,
∴﹣=﹣,即=,
∴∠C=∠B,
∴CE=BE.
25.解:(1)连接DF、DG.
∵BD是⊙O的直径,
∴∠DFB=∠DGB=90°,
∵=,
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A,
∠DGB=∠HDG+∠C,
∴∠A=∠C.
(2)结论:α+β+θ=180°.
理由:如图②中,连接DF,BH.
∵=,
∴∠ADF=∠HBG=θ,
∵∠AFD+∠DFB=180°,∠DFB+∠DHB=180°,
∴∠AFD=∠DHB,
∵∠A+∠ADF+∠AFD=180°,∠AFD=∠DHB=∠C+∠HBG,
∴∠A+θ+∠C+θ=180°,
∴α+β+θ=180
一、选择题
1.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米
B.(4﹣)米
C.2米
D.(4+)米
2.往水平放置的半径为13cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=24cm,则水的最大深度为( )
A.5cm
B.8cm
C.10cm
D.12cm
3.下列说法正确的是( )
A.4的平方根是2
B.平分弦的直径垂直弦并平分弦所对的弧
C.一组数据中有且仅有一个众数
D.等弧所对的弦相等
4.如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A.m
B.m
C.5m
D.m
5.已知,如图,线段AB是⊙O的直径,弦CD⊥AB于点E.若AE=2,CD=6,则OB的长度为( )
A.
B.
C.
D.5
6.如图AB是⊙O的直径,弦CD⊥AB于点E,OC=2cm,CD=2cm,则AE长是( )
A.(+2)cm
B.2cm
C.cm
D.4cm
7.已知⊙O的直径CD=100cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=96cm,则AC的长为( )
A.36cm或64cm
B.60cm或80cm
C.80cm
D.60cm
8.如图,⊙O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP长的取值范围是( )
A.3≤OP≤5
B.4<OP<5
C.4≤OP≤5
D.3<OP<5
9.若弦AB,CD是⊙O的两条平行弦,⊙O的半径为13,AB=10,CD=24,则AB,CD之间的距离为( )
A.7
B.17
C.5或12
D.7或17
10.如图,半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10cm
B.16cm
C.24cm
D.26cm
11.如图,已知⊙O的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为( )
A.3
B.4
C.3
D.4
12.如图,PQ是半⊙O的直径,两正方形彼此相邻且内接于半圆,若小正方形的边长为2cm,则该半圆的直径PQ的长为( )
A.cm
B.cm
C.cm
D.cm
13.如图,在⊙O中,AB,AC为互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D,E,若AB=4,则⊙O的半径是( )
A.
B.2
C.3
D.
14.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
15.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,那么BC等于( )
A.5
B.
C.2
D.
16.如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的度数为( )
A.40°
B.50°
C.60°
D.70°
二、填空题
17.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,AO=5,则OF的长度是
.
18.如图,在半径为2的⊙O中,弦AB与弦CD相交于点M,如果AB=CD=2,∠AMC=120°,那么OM的长为
.
19.如图,扇形OAB中,∠AOB=60°,OA=4+8,点E为弧AB的中点,C为半径OA上一点,将线段CE绕点C逆时针旋转90°得到线段CE′,若点E′恰好落在半径OB上,则OE′=
.
20.如图,AB,CD是⊙O的两条弦,若AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,OE与OF的关系是
(“相等”或“不等”).
三、解答题
21.如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
22.如图,两个同心圆的圆心为O,大圆的弦AB交小圆于C、D,求证:AC=BD.
23.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2.
(1)求OD的长.
(2)求EC的长.
24.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
25.已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且=.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
参考答案
1.解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
2.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:B.
3.解:A、4的平方根为±2,所以A选项的说法错误;
B、平分弦(非直径)的直径垂直弦并平分弦所对的弧,所以B选项的说法错误;
C、一组数据的众数可能有一个,也可能几个,所以C选项的说法错误;
D、等弧所对的弦相等,所以D选项的说法正确.
故选:D.
4.解:连接OB,如图所示:
由题意得:OC⊥AB,
∴AD=BD=AB=2(m),
在Rt△OBD中,根据勾股定理得:OD2+BD2=OB2,
即(OB﹣1)2+22=OB2,
解得:OB=(m),
即这个轮子的半径长为m,
故选:D.
5.解:连接OD,如图所示:
设⊙O的半径为R,
∵弦CD⊥AB于点E.CD=6,
∴DE=CE=CD=3,∠OED=90°,
在Rt△ODE中,由勾股定理得:DE2+OE2=OD2,
即32+(R﹣2)2=R2,
解得:R=,
即OB的长为,故选:B.
6.解:∵弦CD⊥AB于点E,CD=2cm,
∴CE=CD=(cm),
在Rt△OCE中,OC=2cm,
∴OE===(cm),
∴AE=OE+OA=(+2)cm,
故选:A.
7.解:连接AC,AO,
∵⊙O的直径CD=100cm,AB⊥CD,AB=96cm,
∴AM=AB=×96=48(cm),OD=OC=50(cm),
如图1,∵OA=50cm,AM=48cm,CD⊥AB,
∴OM===14(cm),
∴CM=OC+OM=50+14=64(cm),
∴AC===80(cm);
如图2,同理可得,OM=14cm,
∵OC=50cm,
∴MC=50﹣14=36(cm),
在Rt△AMC中,AC==60(cm);
综上所述,AC的长为80cm或60cm,
故选:B.
8.解:连接OA,过点O作OH⊥AB于H,
则AH=HB=AB=3,
由勾股定理得,OH==4,
当点P与点A(或点B)重合时,OP最大,当点P与点H重合时,OP最小,
∴线段OP长的取值范围是4≤OP≤5,
故选:C.
9.解:过O点作OE⊥AB于E,交CD于F,连接OA、OC,如图,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=AB=5,CF=DF=CD=12,
在Rt△OAE中,OE===12,
在Rt△OCF中,OF===5,
当圆心O在AB、CD之间,如图1,EF=OE+OF=12+5=17,
当圆心O不在AB、CD之间,如图2,EF=OE﹣OF=12﹣5=7,
综上所述,AB,CD之间的距离为7或17.
故选:D.
10.解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8cm,OD=13cm,
∴OC=5cm,
又∵OB=13cm,
∴Rt△BCO中,BC==12cm,
∴AB=2BC=24cm.
故选:C.
11.解:连接OB,作OE⊥AB于E,OF⊥CD于F,
则BE=AB=4,四边形PEOF为矩形,
∵AB=CD,OE⊥AB,OF⊥CD,
∴OE=OF,
∴矩形PEOF为正方形,
∴OE=PE,
在Rt△OEB中,OE==3,
∴OP==3,
故选:C.
12.解:如图,过O点作OH⊥BC于H,连接OC、OF,如图,
∵OH⊥BC,
∴BH=CH,
∵∠ODC=∠DCH=90°,
∴四边形ODCH为矩形,
∴CD=OH,OD=CH,
∴OH=2CH,
设OD=xcm,则OH=2xcm,OG=(2+x)cm,
在Rt△OCH中,OC==x(cm),
在Rt△OGF中,22+(2+x)2=(x)2,解得x1=2,x2=﹣1(舍去),
∴OC=2cm,
∴PQ=2OC=4cm.
故选:D.
13.解:∵OD⊥AB,
∴AD=BD=AB,
同理AE=CE=AC,
∵AB=AC=4,
∴AD=AE=2,
连接OA,
∵OD⊥AB,OE⊥AC,AB⊥AC,
∴∠OEA=∠BAC=∠ODA=90°,
∴四边形ADOE为矩形,
又∵AD=AE,
∴四边形ADOE为正方形,
∴OD=AD=2,
∴OA===2,
即⊙O的半径是2,
故选:A.
14.解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
15.解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AB与AC的中点,
∴MN是△ABC的中位线,
∴BC=2MN=2,
故选:C.
16.解:连接OD,如图,
∵扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,
∴BC垂直平分OD,
∴BD=BO,
∵OB=OD,
∴BD=BO=DO,
∴△OBD为等边三角形,
∴∠DOB=60°,
∴∠AOD=∠AOB﹣∠DOB=110°﹣60°=50°,
∴的度数为50°,
故选:B.
17.解:连接OB,
∵弦BD⊥AO,
∴BE=BD=4,
由勾股定理得,OE==3,
则CE=OC+OE=8,
∴BC==4,
∵OF⊥BC,
∴CF=BF=2,
∵∠CFO=∠CEB=90°,∠C=∠C,
∴OF=,
故答案为:.
18.解:如图,过点O作OE⊥AB,OF⊥CD,垂足为E、F,连接OA,
则AE=BE=AB=,CF=DF=CD=,
在Rt△AOE中,
∵OA=2,AE=,
∴OE==1,
∵AB=CD,
∴OE=OF=1,
又∵OM=OM,
∴Rt△OEM≌Rt△OFM(HL),
∴∠OME=∠OMF=∠AMC=60°,
∴OM=,
故答案为:.
19.解:过E点作EH⊥OA于H,过E′点作E′⊥OA于F,连接OE,如图,设OF=x,
∵∠AOB=60°,
∴OE′=2OF=2x,E′F=OF=x,
∵点E为弧AB的中点,
∴∠AOE=∠BOE=∠AOB=30°,
∴EH=OE=(4+8)=2+4,
OH=EH=6+4,
∵线段CE绕点C逆时针旋转90°得到线段CE′,
∴CE=CE′,∠ECE′=90°,
∵∠ECH+∠CEH=90°,∠ECH+∠E′CF=90°,
∴∠CEH=∠E′CF,
在△CEH和△E′CF中
,
∴△CEH≌△E′CF(AAS),
∴CH=E′F=x,CF=EH=2+4,
∵OH=OF+FC+CH,
∴x+2+4+x=6+4,解得x=2,
∴OE′=2x=4.
故答案为4.
20.解:∵OE⊥AB,OF⊥CD,
∴AE=EB,CF=DF,
∵AB=CD,
∴AE=CF,
∵OA=OC,∠AEO=∠CFO,AE=CF,
∴Rt△AEO≌Rt△CFO(HL),
∴OE=OF.
故答案为:相等.
21.解:连接OB,设AB与MN交于点D,如图所示:
∵AC=2,BC=4,
∴AB=AC+BC=6,
∵AB⊥MN,
∴AD=BD=AB=3,∠ODC=∠ODB=90°,
∴CD=AD﹣AC=1,
∴OD===,
∴OB===2,
即⊙O的半径为2.
22.证明:
过O作OE⊥AB于E,
则OE⊥CD,
∵OE过O,
∴由垂径定理得:AE=BE,CE=DE,
∴AE﹣CE=BE﹣DE,
即AC=BD.
23.解:(1)连接BE,
设⊙O半径为r,则OA=OD=r,OC=r﹣2,
∵OD⊥AB,
∴∠ACO=90°,
AC=BC=AB=4,
在Rt△ACO中,由勾股定理得:r2=42+(r﹣2)2,
r=5,
∴OD=r=5;
(2)由(1)得:AE=2r=10,
∵AE为⊙O的直径,
∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中,EC===2.
24.证明:∵AB=CD,
∴=,
∴﹣=﹣,即=,
∴∠C=∠B,
∴CE=BE.
25.解:(1)连接DF、DG.
∵BD是⊙O的直径,
∴∠DFB=∠DGB=90°,
∵=,
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A,
∠DGB=∠HDG+∠C,
∴∠A=∠C.
(2)结论:α+β+θ=180°.
理由:如图②中,连接DF,BH.
∵=,
∴∠ADF=∠HBG=θ,
∵∠AFD+∠DFB=180°,∠DFB+∠DHB=180°,
∴∠AFD=∠DHB,
∵∠A+∠ADF+∠AFD=180°,∠AFD=∠DHB=∠C+∠HBG,
∴∠A+θ+∠C+θ=180°,
∴α+β+θ=180
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
