2.3确定圆的条件 同步能力达标测评 2021-2022学年苏科版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.3确定圆的条件 同步能力达标测评 2021-2022学年苏科版九年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 337.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 09:42:50 | ||
图片预览



文档简介
2021-2022学年苏科版九年级数学上册《2.3确定圆的条件》同步能力达标测评(附答案)
一.选择题(共12小题,满60分)
1.在平面直角坐标系xOy中,若P(3,4)在⊙O内,则⊙O的半径r的取值范围是( )
A.0<r<3
B.r>4
C.0<r<5
D.r>5
2.已知△ABC,AC=3,CB=4,以点C为圆心r为半径作圆,如果点A、点B只有一个点在圆内,那么半径r的取值范围是( )
A.r>3
B.r≥4
C.3<r≤4
D.3≤r≤4
3.⊙O的半径为4,点P到圆心O的距离为d,如果点P在圆内,则d( )
A.d<4
B.d=4
C.d>4
D.0≤d<4
4.如图,⊙A的半径为3,圆心A的坐标为(1,0),点B(m,0)在⊙A内,则m的取值范围是( )
A.m<4
B.m>﹣2
C.﹣2<m<4
D.m<﹣2或m>4
5.在同一平面内,过已知A、B、C三个点可以作圆的个数为( )
A.0个
B.1个
C.2个
D.0个或1个
6.如图,△ABC内接于⊙O,∠AOB=80°,则∠ACB的大小为( )
A.20°
B.40°
C.80°
D.90°
7.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )
A.120°
B.80°
C.60°
D.30°
8.如图,△ABD内接于圆O,∠BAD=60°,AC为圆O的直径.AC交BD于P点且PB=2,PD=4,则AD的长为( )
A.2
B.2
C.2
D.4
9.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
A.O是△AEB的外心,O是△AED的外心
B.O是△AEB的外心,O不是△AED的外心
C.O不是△AEB的外心,O是△AED的外心
D.O不是△AEB的外心,O不是△AED的外心
10.如图,⊙O是△ABC的外接圆,已知∠AOB=120°,则∠ACB等于( )
A.45°
B.30°
C.60°
D.50°
11.有四个命题,其中正确的命题是( )
①经过三点一定可以作一个圆
②任意一个三角形有且只有一个外接圆
③三角形的外心到三角形的三个顶点的距离相等
④在圆中,平分弦的直径一定垂直于这条弦.
①、②、③、④
B.①、②、③
C.②、③、④
D.②、③
12.下列说法正确的是( )
A.三点确定一个圆
B.任意的一个三角形一定有一个外接圆
C.三角形的外心是它的三个角的角平分线的交点
D.任意一个圆有且只有一个内接三角形
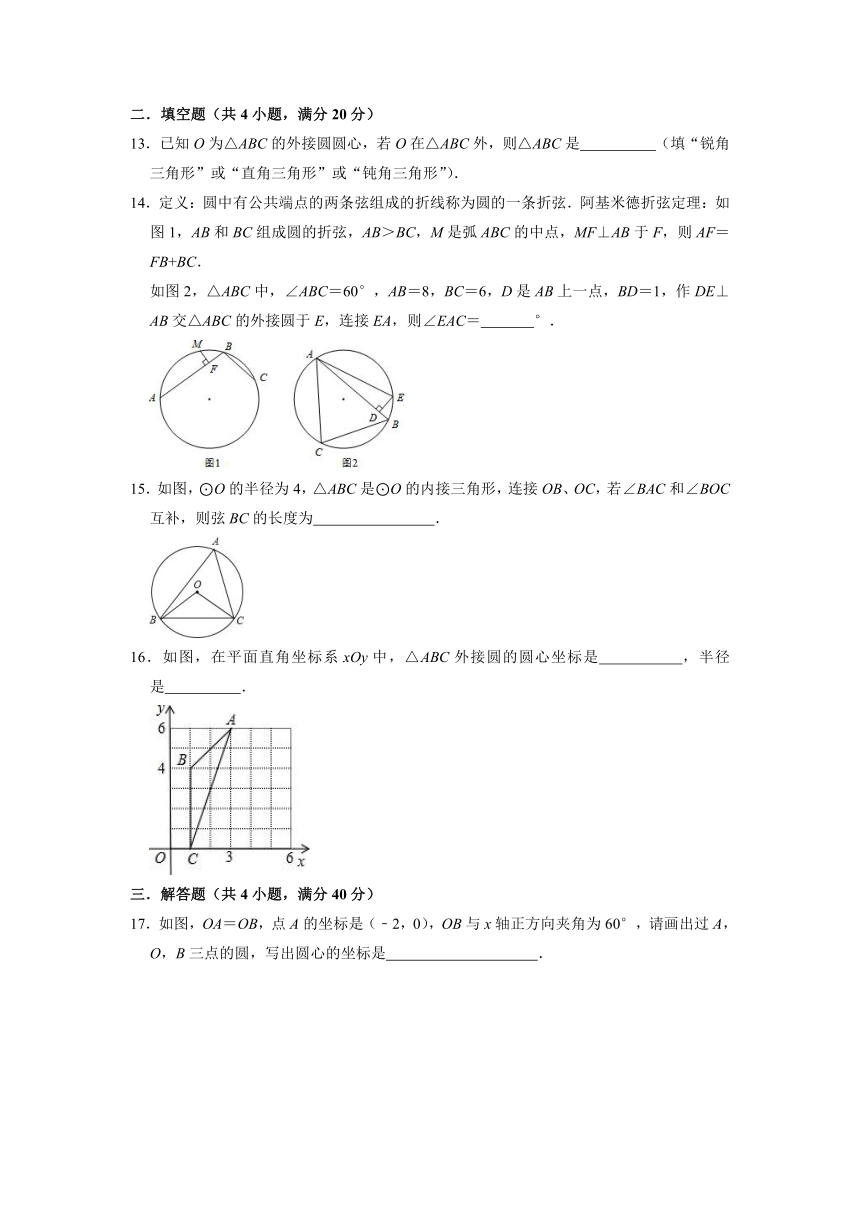
二.填空题(共4小题,满分20分)
13.已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是
(填“锐角三角形”或“直角三角形”或“钝角三角形”).
14.定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.
如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=
°.
15.如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC和∠BOC互补,则弦BC的长度为
.
16.如图,在平面直角坐标系xOy中,△ABC外接圆的圆心坐标是
,半径是
.
三.解答题(共4小题,满分40分)
17.如图,OA=OB,点A的坐标是(﹣2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是
.
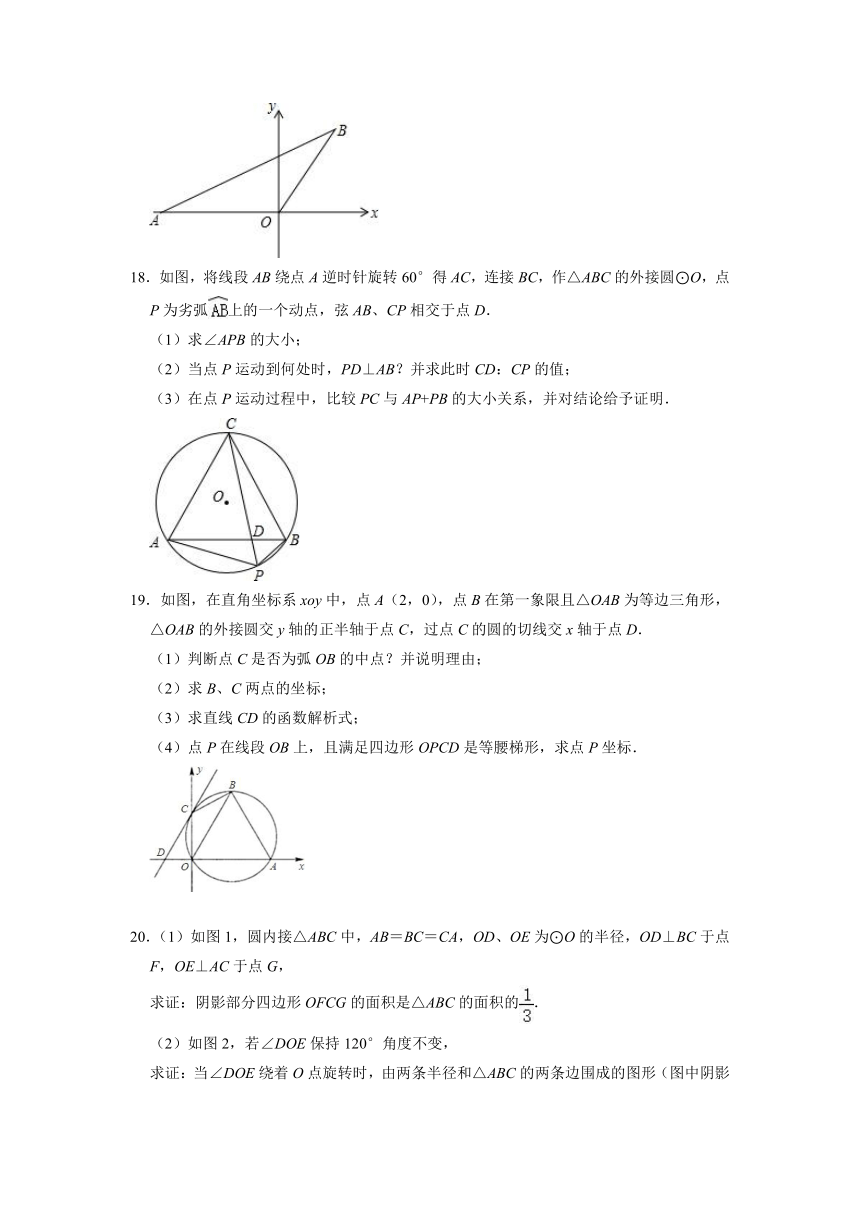
18.如图,将线段AB绕点A逆时针旋转60°得AC,连接BC,作△ABC的外接圆⊙O,点P为劣弧上的一个动点,弦AB、CP相交于点D.
(1)求∠APB的大小;
(2)当点P运动到何处时,PD⊥AB?并求此时CD:CP的值;
(3)在点P运动过程中,比较PC与AP+PB的大小关系,并对结论给予证明.
19.如图,在直角坐标系xoy中,点A(2,0),点B在第一象限且△OAB为等边三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.
(1)判断点C是否为弧OB的中点?并说明理由;
(2)求B、C两点的坐标;
(3)求直线CD的函数解析式;
(4)点P在线段OB上,且满足四边形OPCD是等腰梯形,求点P坐标.
20.(1)如图1,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,
求证:阴影部分四边形OFCG的面积是△ABC的面积的.
(2)如图2,若∠DOE保持120°角度不变,
求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的.
参考答案
一.选择题(共12小题,满分60分)
1.解:∵点P的坐标为(3,4),
∴OP==5,
∵点P(3,4)在⊙O内,
∴OP<r,
即r>5.
故选:D.
2.解:当点A在圆内时点A到点C的距离小于圆的半径,即:r>3;
点B在圆上或圆外时点B到圆心的距离应该不小于圆的半径,即:r≤4;
即3<r≤4.
故选:C.
3.解:∵点P在圆内,且⊙O的半径为4,
∴0≤d<4,
故选:D.
4.解:以A(1,0)为圆心,以3为半径的圆交x轴两点的坐标为(﹣2,0),(4,0),
∵点B(m,0)在以A(1,0)为圆心,以3为半径的圆内,
∴﹣2<m<4.
故选:C.
5.解:当A、B、C三个点共线,过A、B、C三个点不能作圆;
当A、B、C不在同一条直线上,过A、B、C三个点的圆有且只有一个,即三角形的外接圆;
故选:D.
6.解:∵△ABC内接于⊙O,∠AOB=80°,
∴∠ACB=∠AOB=40°.
故选:B.
7.解:∵⊙O是△ABC的外接圆,∠BOC=120°,
∴∠BAC=∠BOC=×120°=60°.
故选:C.
8.解:连接DO并延长交⊙O于E,连接BE,
∵DE是⊙O的直径,
∴∠EBD=90°,
∵∠BED=∠BAD=60°,
∴∠EDB=30°,
∴DE=2BE,
∵PB=2,PD=4,
则BD=6,
∴DE=4,
则OA=OD=2,
又∵∠ODP=∠BDE,
∴∠POD=∠PBE=90°,
∴AD2=OA2+OD2=24,
∴AD=2,
故选:B.
9.解:如图,连接OA、OB、OD.
∵O是△ABC的外心,
∴OA=OB=OC,
∵四边形OCDE是正方形,
∴OA=OB=OE,
∴O是△ABE的外心,
∵OA=OE≠OD,
∴O不是△AED的外心,
故选:B.
10.解:∵∠ACB=∠AOB,∠AOB=120°,
∴∠ACB=60°,
故选:C.
11.解:①不在一条直线上的三个点确定一个圆,故命题错误;
②不在一条直线上的三个点确定一个圆,故命题正确;
③三角形的外心是三角形的三边的中垂线的交点,到三角形的三个顶点的距离相等,故命题正确;
④平分弦(弦不是直径)的直径垂直于弦,故命题错误.
则正确的是:②③.
故选:D.
12.解:∵不在同一条直线上的三个点确定一个圆,任何一个三角形都有一个外接圆,
∴A不正确,B正确;
∵三角形的外心是它的三边垂直平分线的交点,
∴C不正确;
∵任意一个圆由无数个内接三角形,
∴D不正确;
故选:B.
二.填空题(共4小题,满分20分)
13.解:∵锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部.
又∵O为△ABC的外接圆圆心,若O在△ABC外,
∴△ABC是钝角三角形,
故答案为钝角三角形.
14.解:如图2,连接OA、OC、OE,
∵AB=8,BC=6,BD=1,
∴AD=7,BD+BC=7,
∴AD=BD+BC,
而ED⊥AB,
∴点E为弧ABC的中点,即弧AE=弧CE,
∴∠AOE=∠COE,
∵∠AOC=2∠ABC=2×60°=120°,
∴∠AOE=∠COE=120°,
∴∠CAE=∠COE=60°.
故答案为60°.
15.解:过点O作OD⊥BC于D,
则BC=2BD,
∵△ABC内接于⊙O,∠BAC与∠BOC互补,
∴∠BOC=2∠A,∠BOC+∠A=180°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBC=∠OCB=(180°﹣∠BOC)=30°,
∵⊙O的半径为4,
∴BD=2,
∴BC=4.
故答案为:4.
16.解:∵△ABC外接圆的圆心到三角形三个顶点的距离相等,
又∵到B,C两点距离相等的点在BC的垂直平分线上,
∴三角形的外心位置基本确定,只有(5,2)点到三角形三个顶点距离相等,
∴(5,2)点是三角形的外接圆圆心.
利用勾股定理可得半径为:2.
故答案为:(5,2),2.
三.解答题(共4小题,满分40分)
17.解:如图所示:E点即为圆心,
∵OA=OB,点A的坐标是(﹣2,0),OB与x轴正方向夹角为60°,
∴∠EOA=∠BOE=60°,AF=FO=1,
故EF=tan60°FO=,
故圆心的坐标为:(﹣1,).
故答案为:(﹣1,).
18.解:(1)∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵∠APB+∠ACB=180°,
∴∠APB=120°;
(2)当点P运动到的中点时,PD⊥AB,
如图1,连接PC,OA,OB,设⊙O的半径为r,则CP=2r,
又∵⊙O为等边△ABC的外接圆,
∴∠OAB=30°,
在Rt△OAD中,
∵OD=OA=,
∴CD=+r=,
∴CD:CP=:2r=3:4;
(3)PC=AP+PB
证明:方法一:
如图2,在AP的延长线上取点Q,使PQ=PB,连接BQ,
∵∠APB=120°,
∴∠BPQ=60°,
∴△BPQ是等边三角形,
∴PB=BQ,
∵∠CBP=∠CBA+∠ABP=60°+∠ABP,
∠ABQ=∠QBP+∠ABP=60°+∠ABP,
∴∠ABQ=∠CBP,
在△ABQ和△CBP中,PB=QB,∠CBP=∠ABQ,CB=AB,
∴△ABQ≌△CBP,
∴CP=AQ=AP+PQ=AP+PB,即PC=AP+PB;
方法二:如图3,B为圆心,BP为半径画圆交CP于点M,连接BM,
∵∠CPB=60°,
∴△PBM是等边三角形,
∵∠CMB=120°,
∴∠CMB=∠APB,
∴△APB≌△CMB,
∴PC=AP+PB;
方法三:(略证)如图4,以A为圆心,A为半径画圆交CP于N,连接AN,
先证△APN是等边三角形,再证△ANC≌△APB,
从而PC=AP+PB.
19.解:(1)C为弧OB的中点.理由如下:
连接AC;∵OC⊥OA,
∴AC为圆的直径,
∴∠ABC=90°;
∵△OAB为等边三角形,
∴∠ABO=∠AOB=∠BAO=60°,
∵∠ACB=∠AOB=60°,
∴∠COB=∠OBC=30°,
∴弧OC=弧BC;(2分)
即C为弧OB的中点.
(2)过点B作BE⊥OA于E;
∵A(2,0),
∴OA=2,
∴OE=1,BE=,
∴点B的坐标是(1,);
∵C为弧OB的中点,CD是圆的切线,AC为圆的直径,
∴AC⊥CD,AC⊥OB,
∴∠CAO=∠OCD=30°,
∴,
∴C(0,);
(3)在△COD中,∠COD=90°,,
∵∠OCD=∠CAO=∠COD=30°,
∴DC=2DO,
∵CD2=DO2+CO2,
∴(2OD)2=DO2+CO2,
∴OD=,
则有D(﹣,0);
∴直线CD的解析式为:
(4)∵四边形OPCD是等腰梯形,
∴∠CDO=∠DCP=60°,
∴∠OCP=∠COB=30°,
∴PC=PO(8分);
过点P作PF⊥OC于F,则OF=OC=,
∴PF=,
∴点P的坐标为:(,).
20.证明:(1)如图1,连接OA,OC;
∵△ABC是等边三角形,
∴AC=BC,
∵点O是等边三角形ABC的外心,
∴CF=CG=AC,∠OFC=∠OGC=90°,
∴在Rt△OFC和Rt△OGC中,,
∴Rt△OFC≌Rt△OGC.
同理:Rt△OGC≌Rt△OGA.
∴Rt△OFC≌Rt△OGC≌Rt△OGA,
S四边形OFCG=2S△OFC=S△OAC,
∴S△OAC=S△ABC,
∴S四边形OFCG=S△ABC.
(2)证法一:
连接OA,OB和OC,则
△AOC≌△COB≌△BOA,∠1=∠2;
设OD交BC于点F,OE交AC于点G,
∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,
∴∠3=∠5;
在△OAG和△OCF中
,
∴△OAG≌△OCF,
∴S△OAG=S△OCF,
∴S△OAG+S△OGC=S△OCF+S△OGC,
即S四边形OFCG=S△OAC=S△ABC;
证法二:
设OD交BC于点F,OE交AC于点G;
作OH⊥BC,OK⊥AC,垂足分别为H、K;
在四边形HOKC中,∠OHC=∠OKC=90°,∠C=60°,
∴∠HOK=360°﹣90°﹣90°﹣60°=120°,
即∠1+∠2=120度;
又∵∠GOF=∠2+∠3=120°,
∴∠1=∠3,
∵AC=BC,
∴OH=OK,
∴△OGK≌△OFH,
∴S四边形OFCG=S四边形OHCK=S△ABC.
一.选择题(共12小题,满60分)
1.在平面直角坐标系xOy中,若P(3,4)在⊙O内,则⊙O的半径r的取值范围是( )
A.0<r<3
B.r>4
C.0<r<5
D.r>5
2.已知△ABC,AC=3,CB=4,以点C为圆心r为半径作圆,如果点A、点B只有一个点在圆内,那么半径r的取值范围是( )
A.r>3
B.r≥4
C.3<r≤4
D.3≤r≤4
3.⊙O的半径为4,点P到圆心O的距离为d,如果点P在圆内,则d( )
A.d<4
B.d=4
C.d>4
D.0≤d<4
4.如图,⊙A的半径为3,圆心A的坐标为(1,0),点B(m,0)在⊙A内,则m的取值范围是( )
A.m<4
B.m>﹣2
C.﹣2<m<4
D.m<﹣2或m>4
5.在同一平面内,过已知A、B、C三个点可以作圆的个数为( )
A.0个
B.1个
C.2个
D.0个或1个
6.如图,△ABC内接于⊙O,∠AOB=80°,则∠ACB的大小为( )
A.20°
B.40°
C.80°
D.90°
7.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )
A.120°
B.80°
C.60°
D.30°
8.如图,△ABD内接于圆O,∠BAD=60°,AC为圆O的直径.AC交BD于P点且PB=2,PD=4,则AD的长为( )
A.2
B.2
C.2
D.4
9.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
A.O是△AEB的外心,O是△AED的外心
B.O是△AEB的外心,O不是△AED的外心
C.O不是△AEB的外心,O是△AED的外心
D.O不是△AEB的外心,O不是△AED的外心
10.如图,⊙O是△ABC的外接圆,已知∠AOB=120°,则∠ACB等于( )
A.45°
B.30°
C.60°
D.50°
11.有四个命题,其中正确的命题是( )
①经过三点一定可以作一个圆
②任意一个三角形有且只有一个外接圆
③三角形的外心到三角形的三个顶点的距离相等
④在圆中,平分弦的直径一定垂直于这条弦.
①、②、③、④
B.①、②、③
C.②、③、④
D.②、③
12.下列说法正确的是( )
A.三点确定一个圆
B.任意的一个三角形一定有一个外接圆
C.三角形的外心是它的三个角的角平分线的交点
D.任意一个圆有且只有一个内接三角形
二.填空题(共4小题,满分20分)
13.已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是
(填“锐角三角形”或“直角三角形”或“钝角三角形”).
14.定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.
如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=
°.
15.如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC和∠BOC互补,则弦BC的长度为
.
16.如图,在平面直角坐标系xOy中,△ABC外接圆的圆心坐标是
,半径是
.
三.解答题(共4小题,满分40分)
17.如图,OA=OB,点A的坐标是(﹣2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是
.
18.如图,将线段AB绕点A逆时针旋转60°得AC,连接BC,作△ABC的外接圆⊙O,点P为劣弧上的一个动点,弦AB、CP相交于点D.
(1)求∠APB的大小;
(2)当点P运动到何处时,PD⊥AB?并求此时CD:CP的值;
(3)在点P运动过程中,比较PC与AP+PB的大小关系,并对结论给予证明.
19.如图,在直角坐标系xoy中,点A(2,0),点B在第一象限且△OAB为等边三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.
(1)判断点C是否为弧OB的中点?并说明理由;
(2)求B、C两点的坐标;
(3)求直线CD的函数解析式;
(4)点P在线段OB上,且满足四边形OPCD是等腰梯形,求点P坐标.
20.(1)如图1,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,
求证:阴影部分四边形OFCG的面积是△ABC的面积的.
(2)如图2,若∠DOE保持120°角度不变,
求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的.
参考答案
一.选择题(共12小题,满分60分)
1.解:∵点P的坐标为(3,4),
∴OP==5,
∵点P(3,4)在⊙O内,
∴OP<r,
即r>5.
故选:D.
2.解:当点A在圆内时点A到点C的距离小于圆的半径,即:r>3;
点B在圆上或圆外时点B到圆心的距离应该不小于圆的半径,即:r≤4;
即3<r≤4.
故选:C.
3.解:∵点P在圆内,且⊙O的半径为4,
∴0≤d<4,
故选:D.
4.解:以A(1,0)为圆心,以3为半径的圆交x轴两点的坐标为(﹣2,0),(4,0),
∵点B(m,0)在以A(1,0)为圆心,以3为半径的圆内,
∴﹣2<m<4.
故选:C.
5.解:当A、B、C三个点共线,过A、B、C三个点不能作圆;
当A、B、C不在同一条直线上,过A、B、C三个点的圆有且只有一个,即三角形的外接圆;
故选:D.
6.解:∵△ABC内接于⊙O,∠AOB=80°,
∴∠ACB=∠AOB=40°.
故选:B.
7.解:∵⊙O是△ABC的外接圆,∠BOC=120°,
∴∠BAC=∠BOC=×120°=60°.
故选:C.
8.解:连接DO并延长交⊙O于E,连接BE,
∵DE是⊙O的直径,
∴∠EBD=90°,
∵∠BED=∠BAD=60°,
∴∠EDB=30°,
∴DE=2BE,
∵PB=2,PD=4,
则BD=6,
∴DE=4,
则OA=OD=2,
又∵∠ODP=∠BDE,
∴∠POD=∠PBE=90°,
∴AD2=OA2+OD2=24,
∴AD=2,
故选:B.
9.解:如图,连接OA、OB、OD.
∵O是△ABC的外心,
∴OA=OB=OC,
∵四边形OCDE是正方形,
∴OA=OB=OE,
∴O是△ABE的外心,
∵OA=OE≠OD,
∴O不是△AED的外心,
故选:B.
10.解:∵∠ACB=∠AOB,∠AOB=120°,
∴∠ACB=60°,
故选:C.
11.解:①不在一条直线上的三个点确定一个圆,故命题错误;
②不在一条直线上的三个点确定一个圆,故命题正确;
③三角形的外心是三角形的三边的中垂线的交点,到三角形的三个顶点的距离相等,故命题正确;
④平分弦(弦不是直径)的直径垂直于弦,故命题错误.
则正确的是:②③.
故选:D.
12.解:∵不在同一条直线上的三个点确定一个圆,任何一个三角形都有一个外接圆,
∴A不正确,B正确;
∵三角形的外心是它的三边垂直平分线的交点,
∴C不正确;
∵任意一个圆由无数个内接三角形,
∴D不正确;
故选:B.
二.填空题(共4小题,满分20分)
13.解:∵锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部.
又∵O为△ABC的外接圆圆心,若O在△ABC外,
∴△ABC是钝角三角形,
故答案为钝角三角形.
14.解:如图2,连接OA、OC、OE,
∵AB=8,BC=6,BD=1,
∴AD=7,BD+BC=7,
∴AD=BD+BC,
而ED⊥AB,
∴点E为弧ABC的中点,即弧AE=弧CE,
∴∠AOE=∠COE,
∵∠AOC=2∠ABC=2×60°=120°,
∴∠AOE=∠COE=120°,
∴∠CAE=∠COE=60°.
故答案为60°.
15.解:过点O作OD⊥BC于D,
则BC=2BD,
∵△ABC内接于⊙O,∠BAC与∠BOC互补,
∴∠BOC=2∠A,∠BOC+∠A=180°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBC=∠OCB=(180°﹣∠BOC)=30°,
∵⊙O的半径为4,
∴BD=2,
∴BC=4.
故答案为:4.
16.解:∵△ABC外接圆的圆心到三角形三个顶点的距离相等,
又∵到B,C两点距离相等的点在BC的垂直平分线上,
∴三角形的外心位置基本确定,只有(5,2)点到三角形三个顶点距离相等,
∴(5,2)点是三角形的外接圆圆心.
利用勾股定理可得半径为:2.
故答案为:(5,2),2.
三.解答题(共4小题,满分40分)
17.解:如图所示:E点即为圆心,
∵OA=OB,点A的坐标是(﹣2,0),OB与x轴正方向夹角为60°,
∴∠EOA=∠BOE=60°,AF=FO=1,
故EF=tan60°FO=,
故圆心的坐标为:(﹣1,).
故答案为:(﹣1,).
18.解:(1)∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵∠APB+∠ACB=180°,
∴∠APB=120°;
(2)当点P运动到的中点时,PD⊥AB,
如图1,连接PC,OA,OB,设⊙O的半径为r,则CP=2r,
又∵⊙O为等边△ABC的外接圆,
∴∠OAB=30°,
在Rt△OAD中,
∵OD=OA=,
∴CD=+r=,
∴CD:CP=:2r=3:4;
(3)PC=AP+PB
证明:方法一:
如图2,在AP的延长线上取点Q,使PQ=PB,连接BQ,
∵∠APB=120°,
∴∠BPQ=60°,
∴△BPQ是等边三角形,
∴PB=BQ,
∵∠CBP=∠CBA+∠ABP=60°+∠ABP,
∠ABQ=∠QBP+∠ABP=60°+∠ABP,
∴∠ABQ=∠CBP,
在△ABQ和△CBP中,PB=QB,∠CBP=∠ABQ,CB=AB,
∴△ABQ≌△CBP,
∴CP=AQ=AP+PQ=AP+PB,即PC=AP+PB;
方法二:如图3,B为圆心,BP为半径画圆交CP于点M,连接BM,
∵∠CPB=60°,
∴△PBM是等边三角形,
∵∠CMB=120°,
∴∠CMB=∠APB,
∴△APB≌△CMB,
∴PC=AP+PB;
方法三:(略证)如图4,以A为圆心,A为半径画圆交CP于N,连接AN,
先证△APN是等边三角形,再证△ANC≌△APB,
从而PC=AP+PB.
19.解:(1)C为弧OB的中点.理由如下:
连接AC;∵OC⊥OA,
∴AC为圆的直径,
∴∠ABC=90°;
∵△OAB为等边三角形,
∴∠ABO=∠AOB=∠BAO=60°,
∵∠ACB=∠AOB=60°,
∴∠COB=∠OBC=30°,
∴弧OC=弧BC;(2分)
即C为弧OB的中点.
(2)过点B作BE⊥OA于E;
∵A(2,0),
∴OA=2,
∴OE=1,BE=,
∴点B的坐标是(1,);
∵C为弧OB的中点,CD是圆的切线,AC为圆的直径,
∴AC⊥CD,AC⊥OB,
∴∠CAO=∠OCD=30°,
∴,
∴C(0,);
(3)在△COD中,∠COD=90°,,
∵∠OCD=∠CAO=∠COD=30°,
∴DC=2DO,
∵CD2=DO2+CO2,
∴(2OD)2=DO2+CO2,
∴OD=,
则有D(﹣,0);
∴直线CD的解析式为:
(4)∵四边形OPCD是等腰梯形,
∴∠CDO=∠DCP=60°,
∴∠OCP=∠COB=30°,
∴PC=PO(8分);
过点P作PF⊥OC于F,则OF=OC=,
∴PF=,
∴点P的坐标为:(,).
20.证明:(1)如图1,连接OA,OC;
∵△ABC是等边三角形,
∴AC=BC,
∵点O是等边三角形ABC的外心,
∴CF=CG=AC,∠OFC=∠OGC=90°,
∴在Rt△OFC和Rt△OGC中,,
∴Rt△OFC≌Rt△OGC.
同理:Rt△OGC≌Rt△OGA.
∴Rt△OFC≌Rt△OGC≌Rt△OGA,
S四边形OFCG=2S△OFC=S△OAC,
∴S△OAC=S△ABC,
∴S四边形OFCG=S△ABC.
(2)证法一:
连接OA,OB和OC,则
△AOC≌△COB≌△BOA,∠1=∠2;
设OD交BC于点F,OE交AC于点G,
∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,
∴∠3=∠5;
在△OAG和△OCF中
,
∴△OAG≌△OCF,
∴S△OAG=S△OCF,
∴S△OAG+S△OGC=S△OCF+S△OGC,
即S四边形OFCG=S△OAC=S△ABC;
证法二:
设OD交BC于点F,OE交AC于点G;
作OH⊥BC,OK⊥AC,垂足分别为H、K;
在四边形HOKC中,∠OHC=∠OKC=90°,∠C=60°,
∴∠HOK=360°﹣90°﹣90°﹣60°=120°,
即∠1+∠2=120度;
又∵∠GOF=∠2+∠3=120°,
∴∠1=∠3,
∵AC=BC,
∴OH=OK,
∴△OGK≌△OFH,
∴S四边形OFCG=S四边形OHCK=S△ABC.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
