北师大版2021--2022八年级(上)数学第三章 位置与坐标单元质量检测试卷A(含解析)
文档属性
| 名称 | 北师大版2021--2022八年级(上)数学第三章 位置与坐标单元质量检测试卷A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 11:19:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2021-20202年八年级(上)第三章位置与坐标检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
如图所示,是阅兵中轰炸机梯队的其中一部分飞行队形,如果
,
两架轰炸机的平面坐标分别是
和
,那么轰炸机
的平面坐标是
A.
B.
C.
D.
2.
已知点
,,点
,过点
作
轴的平行线交直线
于点
,则线段
的长为
A.
B.
C.
D.
3.
在平面直角坐标系中,
关于
轴对称的点的坐标为
A.
B.
C.
D.
4.
已知点
的坐标为
,点
的坐标为
,点
在
轴上,
的面积是
,则点
的坐标可能是
A.
B.
C.
D.
5.
如图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、
正北方向为
轴、
轴的正方向,表示群明湖的点的坐标为
,表示冰壶馆的点的坐标为
,则表示下列场馆建筑的点的坐标正确的是
A.
滑雪大跳台
B.
五一剧场
C.
冬奥组委会
D.
全民畅读艺术书店
6.
若
是任意实数,则点
一定不在
A.
第一象限内
B.
第二象限内
C.
第三象限内
D.
第四象限内
7.
已知点
的坐标为
,点
的坐标为
,点
在
轴上,
的面积是
,则点
的坐标可能是
A.
B.
C.
D.
8.
共享单车提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车APP,如图所示,“”为小白同学的位置,“”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是
A.
B.
C.
D.
9.
如图所示的坐标平面上有原点
与
,,,
四点.若有一直线
通过点
且与
轴垂直,则
也会经过
A.
点
B.
点
C.
点
D.
点
10.
点
关于
轴对称的点是
A.
B.
C.
D.
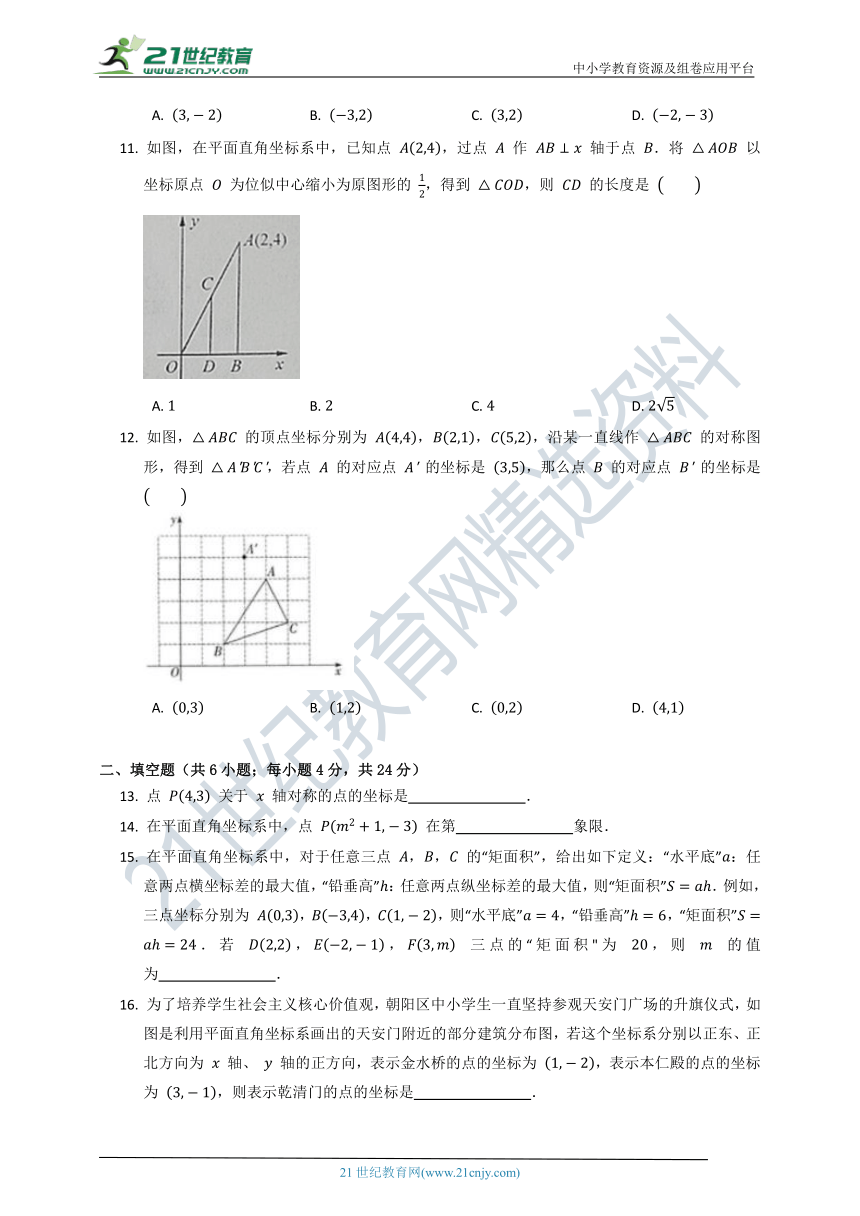
11.
如图,在平面直角坐标系中,已知点
,过点
作
轴于点
.将
以坐标原点
为位似中心缩小为原图形的
,得到
,则
的长度是
A.
B.
C.
D.
12.
如图,
的顶点坐标分别为
,,,沿某一直线作
的对称图形,得到
,若点
的对应点
的坐标是
,那么点
的对应点
的坐标是
A.
B.
C.
D.
二、填空题(共6小题;每小题4分,共24分)
13.
点
关于
轴对称的点的坐标是
.
14.
在平面直角坐标系中,点
在第
象限.
15.
在平面直角坐标系中,对于任意三点
,,
的“矩面积”,给出如下定义:“水平底”:任意两点横坐标差的最大值,“铅垂高”:任意两点纵坐标差的最大值,则“矩面积”.例如,三点坐标分别为
,,,则“水平底”,“铅垂高”,“矩面积”.若
,,
三点的“矩面积"为
,则
的值为
.
16.
为了培养学生社会主义核心价值观,朝阳区中小学生一直坚持参观天安门广场的升旗仪式,如图是利用平面直角坐标系画出的天安门附近的部分建筑分布图,若这个坐标系分别以正东、正北方向为
轴、
轴的正方向,表示金水桥的点的坐标为
,表示本仁殿的点的坐标为
,则表示乾清门的点的坐标是
.
17.
如图,在平面直角坐标系中,已知点
的坐标为
,若
是关于直线
的轴对称图形,则点
的坐标为
;若
是关于直线
的轴对称图形,则点
的坐标为
.
18.
如图,将一等边三角形的三条边各
等分,按顺时针方向(图中箭头方向)标注各等分点的序号
,,,,,,,,,将不同边上的序号和为
的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点
的坐标可表示为
,点
的坐标可表示为
,按此方法,则点
的坐标可表示为
.
三、解答题(共7小题;共60分)
19.
(8分)在同一平面直角坐标系中,描出下列各组的点,并将各组的点用线段依次连接起来,观察各组所得的图形,它们分别像什么
(1),,,,;
(2),,,,.
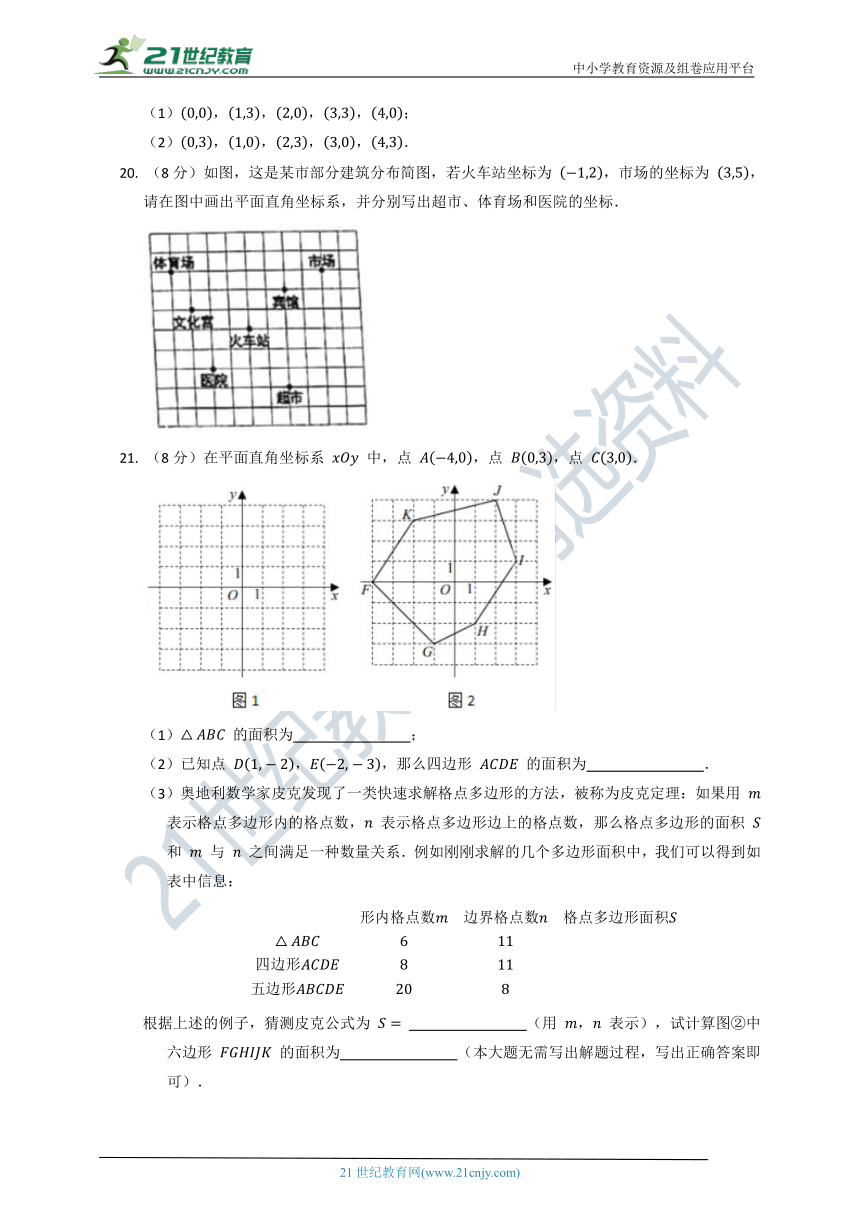
20.
(8分)如图,这是某市部分建筑分布简图,若火车站坐标为
,市场的坐标为
,请在图中画出平面直角坐标系,并分别写出超市、体育场和医院的坐标.
21.
(8分)在平面直角坐标系
中,点
,点
,点
.
(1)
的面积为
;
(2)已知点
,,那么四边形
的面积为
.
(3)奥地利数学家皮克发现了一类快速求解格点多边形的方法,被称为皮克定理:如果用
表示格点多边形内的格点数,
表示格点多边形边上的格点数,那么格点多边形的面积
和
与
之间满足一种数量关系.例如刚刚求解的几个多边形面积中,我们可以得到如表中信息:
根据上述的例子,猜测皮克公式为
(用
,
表示),试计算图②中六边形
的面积为
(本大题无需写出解题过程,写出正确答案即可).
22.
(8分)如图,在平面直角坐标系中,,,在
轴上找一点
,使得
最短,请直接写出点
的坐标.
23.
(10分)回答下列各题.
(1)已知点
的横坐标减纵坐标的差为
,求点
到
轴、
轴的距离;
(2)已知点
到两坐标轴的距离相等,且在第二象限,求点
的坐标;
(3)已知线段
平行于
轴,点
的坐标为
,且
,求点
的坐标.
24.
(10分)下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.
(1)写出游乐场和糖果店的坐标;
(2)某星期日早晨,小红同学从家里出发,沿着
,,,,
的路线转了一下,又回到家里,写出路上她经过的地方.
25.
(8分)如图,在平面直角坐标系中,分别写出
的顶点坐标,并求出
的面积.
答案
第一部分
1.
B
【解析】因为
和
,所以点
的坐标为
.
2.
C
3.
A
4.
C
【解析】设点
的坐标是
,
根据题意得,,即
,
解得
,
所以点
的坐标是
或
.
故选C.
5.
A
6.
D
【解析】因为
,
所以点
的纵坐标一定大于横坐标,
因为第四象限内的点的横坐标是正数,纵坐标是负数,
所以在第四象限内的点的横坐标一定大于纵坐标,
所以点
一定不在第四象限内,故选D.
7.
C
【解析】设点
的坐标是
,
根据题意得,,
即
,
解得
.
所以点
的坐标是
或
.
8.
A
【解析】观察图形,根据点的位置,可得答案.
9.
D
【解析】
点
与点
的纵坐标相同,
会经过点
.
10.
B
11.
A
【解析】
点
,过点
作
轴于点
,将
以坐标原点
为位似中心缩小为原图形的
,得到
,
,则
的长度是:.
故选:A.
12.
A
【解析】如图所示,.
第二部分
13.
14.
四
15.
或
【解析】,,,
“水平底”,“铅垂高”.
①当
时,三点的“矩面积”,不合题意;
②当
时,三点的“矩面积”,
解得
或
(舍去);
③当
时,三点的“矩面积”,
解得
或
(舍去).
综上,.
16.
17.
,
【解析】根据题意得,点
和点
关于直线
对称,
它们到
的距离相等,是
个单位长度,又
轴,
点
的坐标是
.若
是关于直线
的轴对称图形,则点
的横坐标为
,纵坐标为
,
点
的坐标为
.
18.
【解析】根据点
的坐标可表示为
,点
的坐标可表示为
可知,点
的坐标可表示为
.
第三部分
19.
(1)
描点,连线略,像大写字母M.
(2)
描点,连线略,像大写字母W.
20.
平面直角坐标系略,超市的坐标为
,体育场的坐标为
,医院的坐标为
.
21.
(1)
【解析】
的底为
,高为
,所以面积为
.
(2)
【解析】四边形
的面积可以通过多种方法求出,以下为其中一种:.
(3)
;
【解析】皮克公式为
,六边形
的面积为
.
22.
如图,点
即为所求,点
的坐标为
.
23.
(1)
根据题意,得
,解得
,
,,
点的坐标为
,
点
到
轴的距离是
,到
轴的距离是
.
(2)
点
到两坐标轴的距离相等,
,即
或
,解得
或
.
当
时,点
的坐标为
,位于第一象限,不满足题意;当
时,点
的坐标为
,位于第二象限,满足题意,
点
的坐标为
.
(3)
线段
平行于
轴,点
的坐标为
,
点
的横坐标是
,
又
,
当点
在点
上方时,点
的纵坐标是
,当点
在点
下方时,点
的纵坐标是
,
点
的坐标是
或
.
24.
(1)
游乐场的坐标是
,糖果店的坐标是
;
(2)
由小红同学从家里出发,沿着
,,,,
的路线转了一下,到学校
公园
姥姥家
宠物店
邮局.
25.
由图知,
的顶点坐标分别是
,,,
答:三角形
的面积是
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
北师大版2021-20202年八年级(上)第三章位置与坐标检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
如图所示,是阅兵中轰炸机梯队的其中一部分飞行队形,如果
,
两架轰炸机的平面坐标分别是
和
,那么轰炸机
的平面坐标是
A.
B.
C.
D.
2.
已知点
,,点
,过点
作
轴的平行线交直线
于点
,则线段
的长为
A.
B.
C.
D.
3.
在平面直角坐标系中,
关于
轴对称的点的坐标为
A.
B.
C.
D.
4.
已知点
的坐标为
,点
的坐标为
,点
在
轴上,
的面积是
,则点
的坐标可能是
A.
B.
C.
D.
5.
如图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、
正北方向为
轴、
轴的正方向,表示群明湖的点的坐标为
,表示冰壶馆的点的坐标为
,则表示下列场馆建筑的点的坐标正确的是
A.
滑雪大跳台
B.
五一剧场
C.
冬奥组委会
D.
全民畅读艺术书店
6.
若
是任意实数,则点
一定不在
A.
第一象限内
B.
第二象限内
C.
第三象限内
D.
第四象限内
7.
已知点
的坐标为
,点
的坐标为
,点
在
轴上,
的面积是
,则点
的坐标可能是
A.
B.
C.
D.
8.
共享单车提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车APP,如图所示,“”为小白同学的位置,“”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是
A.
B.
C.
D.
9.
如图所示的坐标平面上有原点
与
,,,
四点.若有一直线
通过点
且与
轴垂直,则
也会经过
A.
点
B.
点
C.
点
D.
点
10.
点
关于
轴对称的点是
A.
B.
C.
D.
11.
如图,在平面直角坐标系中,已知点
,过点
作
轴于点
.将
以坐标原点
为位似中心缩小为原图形的
,得到
,则
的长度是
A.
B.
C.
D.
12.
如图,
的顶点坐标分别为
,,,沿某一直线作
的对称图形,得到
,若点
的对应点
的坐标是
,那么点
的对应点
的坐标是
A.
B.
C.
D.
二、填空题(共6小题;每小题4分,共24分)
13.
点
关于
轴对称的点的坐标是
.
14.
在平面直角坐标系中,点
在第
象限.
15.
在平面直角坐标系中,对于任意三点
,,
的“矩面积”,给出如下定义:“水平底”:任意两点横坐标差的最大值,“铅垂高”:任意两点纵坐标差的最大值,则“矩面积”.例如,三点坐标分别为
,,,则“水平底”,“铅垂高”,“矩面积”.若
,,
三点的“矩面积"为
,则
的值为
.
16.
为了培养学生社会主义核心价值观,朝阳区中小学生一直坚持参观天安门广场的升旗仪式,如图是利用平面直角坐标系画出的天安门附近的部分建筑分布图,若这个坐标系分别以正东、正北方向为
轴、
轴的正方向,表示金水桥的点的坐标为
,表示本仁殿的点的坐标为
,则表示乾清门的点的坐标是
.
17.
如图,在平面直角坐标系中,已知点
的坐标为
,若
是关于直线
的轴对称图形,则点
的坐标为
;若
是关于直线
的轴对称图形,则点
的坐标为
.
18.
如图,将一等边三角形的三条边各
等分,按顺时针方向(图中箭头方向)标注各等分点的序号
,,,,,,,,,将不同边上的序号和为
的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始,按顺时针方向),如点
的坐标可表示为
,点
的坐标可表示为
,按此方法,则点
的坐标可表示为
.
三、解答题(共7小题;共60分)
19.
(8分)在同一平面直角坐标系中,描出下列各组的点,并将各组的点用线段依次连接起来,观察各组所得的图形,它们分别像什么
(1),,,,;
(2),,,,.
20.
(8分)如图,这是某市部分建筑分布简图,若火车站坐标为
,市场的坐标为
,请在图中画出平面直角坐标系,并分别写出超市、体育场和医院的坐标.
21.
(8分)在平面直角坐标系
中,点
,点
,点
.
(1)
的面积为
;
(2)已知点
,,那么四边形
的面积为
.
(3)奥地利数学家皮克发现了一类快速求解格点多边形的方法,被称为皮克定理:如果用
表示格点多边形内的格点数,
表示格点多边形边上的格点数,那么格点多边形的面积
和
与
之间满足一种数量关系.例如刚刚求解的几个多边形面积中,我们可以得到如表中信息:
根据上述的例子,猜测皮克公式为
(用
,
表示),试计算图②中六边形
的面积为
(本大题无需写出解题过程,写出正确答案即可).
22.
(8分)如图,在平面直角坐标系中,,,在
轴上找一点
,使得
最短,请直接写出点
的坐标.
23.
(10分)回答下列各题.
(1)已知点
的横坐标减纵坐标的差为
,求点
到
轴、
轴的距离;
(2)已知点
到两坐标轴的距离相等,且在第二象限,求点
的坐标;
(3)已知线段
平行于
轴,点
的坐标为
,且
,求点
的坐标.
24.
(10分)下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.
(1)写出游乐场和糖果店的坐标;
(2)某星期日早晨,小红同学从家里出发,沿着
,,,,
的路线转了一下,又回到家里,写出路上她经过的地方.
25.
(8分)如图,在平面直角坐标系中,分别写出
的顶点坐标,并求出
的面积.
答案
第一部分
1.
B
【解析】因为
和
,所以点
的坐标为
.
2.
C
3.
A
4.
C
【解析】设点
的坐标是
,
根据题意得,,即
,
解得
,
所以点
的坐标是
或
.
故选C.
5.
A
6.
D
【解析】因为
,
所以点
的纵坐标一定大于横坐标,
因为第四象限内的点的横坐标是正数,纵坐标是负数,
所以在第四象限内的点的横坐标一定大于纵坐标,
所以点
一定不在第四象限内,故选D.
7.
C
【解析】设点
的坐标是
,
根据题意得,,
即
,
解得
.
所以点
的坐标是
或
.
8.
A
【解析】观察图形,根据点的位置,可得答案.
9.
D
【解析】
点
与点
的纵坐标相同,
会经过点
.
10.
B
11.
A
【解析】
点
,过点
作
轴于点
,将
以坐标原点
为位似中心缩小为原图形的
,得到
,
,则
的长度是:.
故选:A.
12.
A
【解析】如图所示,.
第二部分
13.
14.
四
15.
或
【解析】,,,
“水平底”,“铅垂高”.
①当
时,三点的“矩面积”,不合题意;
②当
时,三点的“矩面积”,
解得
或
(舍去);
③当
时,三点的“矩面积”,
解得
或
(舍去).
综上,.
16.
17.
,
【解析】根据题意得,点
和点
关于直线
对称,
它们到
的距离相等,是
个单位长度,又
轴,
点
的坐标是
.若
是关于直线
的轴对称图形,则点
的横坐标为
,纵坐标为
,
点
的坐标为
.
18.
【解析】根据点
的坐标可表示为
,点
的坐标可表示为
可知,点
的坐标可表示为
.
第三部分
19.
(1)
描点,连线略,像大写字母M.
(2)
描点,连线略,像大写字母W.
20.
平面直角坐标系略,超市的坐标为
,体育场的坐标为
,医院的坐标为
.
21.
(1)
【解析】
的底为
,高为
,所以面积为
.
(2)
【解析】四边形
的面积可以通过多种方法求出,以下为其中一种:.
(3)
;
【解析】皮克公式为
,六边形
的面积为
.
22.
如图,点
即为所求,点
的坐标为
.
23.
(1)
根据题意,得
,解得
,
,,
点的坐标为
,
点
到
轴的距离是
,到
轴的距离是
.
(2)
点
到两坐标轴的距离相等,
,即
或
,解得
或
.
当
时,点
的坐标为
,位于第一象限,不满足题意;当
时,点
的坐标为
,位于第二象限,满足题意,
点
的坐标为
.
(3)
线段
平行于
轴,点
的坐标为
,
点
的横坐标是
,
又
,
当点
在点
上方时,点
的纵坐标是
,当点
在点
下方时,点
的纵坐标是
,
点
的坐标是
或
.
24.
(1)
游乐场的坐标是
,糖果店的坐标是
;
(2)
由小红同学从家里出发,沿着
,,,,
的路线转了一下,到学校
公园
姥姥家
宠物店
邮局.
25.
由图知,
的顶点坐标分别是
,,,
答:三角形
的面积是
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
