北师大版2021--2022八年级(上)数学第三章 位置与坐标单元质量检测试卷B(含解析)
文档属性
| 名称 | 北师大版2021--2022八年级(上)数学第三章 位置与坐标单元质量检测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 11:21:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2021-2022学年八年级(上)第三章位置与坐标检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共,36分)
1.
已知点
关于
轴的对称点是点
,那么点
为
A.
B.
C.
D.
2.
在平面直角坐标系中,点
在
轴上方,
轴的左侧,距离
轴
个单位长度,距离
轴
个单位长度,则点
的坐标为
A.
B.
C.
D.
3.
如图是某市地图简图的一部分,图中“故宫”“鼓楼”所在的区域分别是
A.
,
B.
,
C.
,
D.
,
4.
数学中有许多形状优美、寓意美好的曲线,曲线
就是其中之一(如图).给出下列三个结论:
①曲线
恰好经过
个整点(即横、纵坐标均为整数的点);
②曲线
在第一、二象限中的任意一点到原点的距离大于
;
③曲线
所围成的“心形”区域的面积小于
.
其中正确结论的序号是
A.
①
B.
②
C.
①②
D.
①②③
5.
在平面直角坐标系中,点
关于
轴对称的点的坐标为
A.
B.
C.
D.
6.
在平面直角坐标系中,点
位于
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
7.
年
月
日,云南省瑞丽市共增加
例新冠肺炎确诊病例,均为缅甸输入.下列表述中,能确定瑞丽市位置的是
A.
云南西部
B.
云南与缅甸交界处
C.
东经
D.
东经
,北纬
8.
若点
,
关于
轴对称,则
A.
,
B.
,
C.
,
D.
,
9.
若
在第二象限,则点
在第
象限.
A.
一
B.
二
C.
三
D.
四
10.
下图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为
轴、
轴的正方向建立平面直角坐标系.
有如下四个结论:
①当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
;
②当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
;
③当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
;
④当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
.
上述结论中,所有正确结论的序号是
A.
①②③
B.
②③④
C.
①④
D.
①②③④
11.
已知
和
两点,且
与坐标轴围成的三角形的面积等于
,则
的值为
A.
B.
C.
或
D.
或
12.
已知点
,,点
在
轴上,且
的面积为
,则点
的坐标为
A.
B.
C.
或
D.
无法确定
二、填空题(共6小题;每小题4分,共24分)
13.
在平面上有
,
两点,若以点
为原点建立平面直角坐标系,则点
坐标为
.若以点
为原点建立平面直角坐标系,则点
的坐标为
.
14.
七()班座位有
排
列,张艳的座位在
排
列,简记为
,班级座次表上写着王刚
,那么王刚的座位在
.
15.
若点
与点
关于
轴对称,则
的值是
.
16.
在平面直角坐标系
中,已知三角形的三个顶点的坐标分别是
,,,点
在
轴上,设三角形
和三角形
的面积分别为
和
,如果
,那么点
的纵坐标
的取值范围是
.
17.
已知点
是直角坐标平面内的点,若
,则点
在第
象限.
18.
如图,小强告诉小华图中,两点的坐标分别为,,,,小华一下就说出了在同一坐标系下的坐标
.
三、解答题(共7小题;共60分)
19.
(8分)如图是某战役缴获敌人防御工事坐标地图的碎片,依稀可见:一号暗堡
的坐标为
,五号暗堡
的坐标为
.另有情报得知敌军指挥部的坐标为
.请问你能找到敌军的指挥部吗
20.
(8分)在如图所示的正方形网格中,每个小正方形的边长都是
,
顶点都在网格线的交点上,点
的坐标为
,点
的坐标为
.
(1)()根据上述条件,在网格中建立平面直角坐标系
;
()画出
关于
轴对称的图形
;
(2)写出点
关于
轴对称的点的坐标.
21.(8分)
年
月
日新版《北京市生活垃圾管理条例》实施,意味着北京市垃圾分类正式进入法治化、常态化、系统化轨道.条例明确规定,将垃圾分为厨余垃圾、有害垃圾、其他垃圾和可回收物
类.为了帮助同学们养成垃圾分类的好习惯,七年级一班计划以此为主题召开一次班会,需要一部分同学手绘可回收物的标识小卡片(如图).发给大家的纸张和样图中的纸张一样,都是边长为
的正方形.为了让大家画的标志在纸张中的位置大小尽可能的一致.标志中标注了
,,
三个关键点,请你通过测量告诉大家
,,
三点在纸张中的位置.
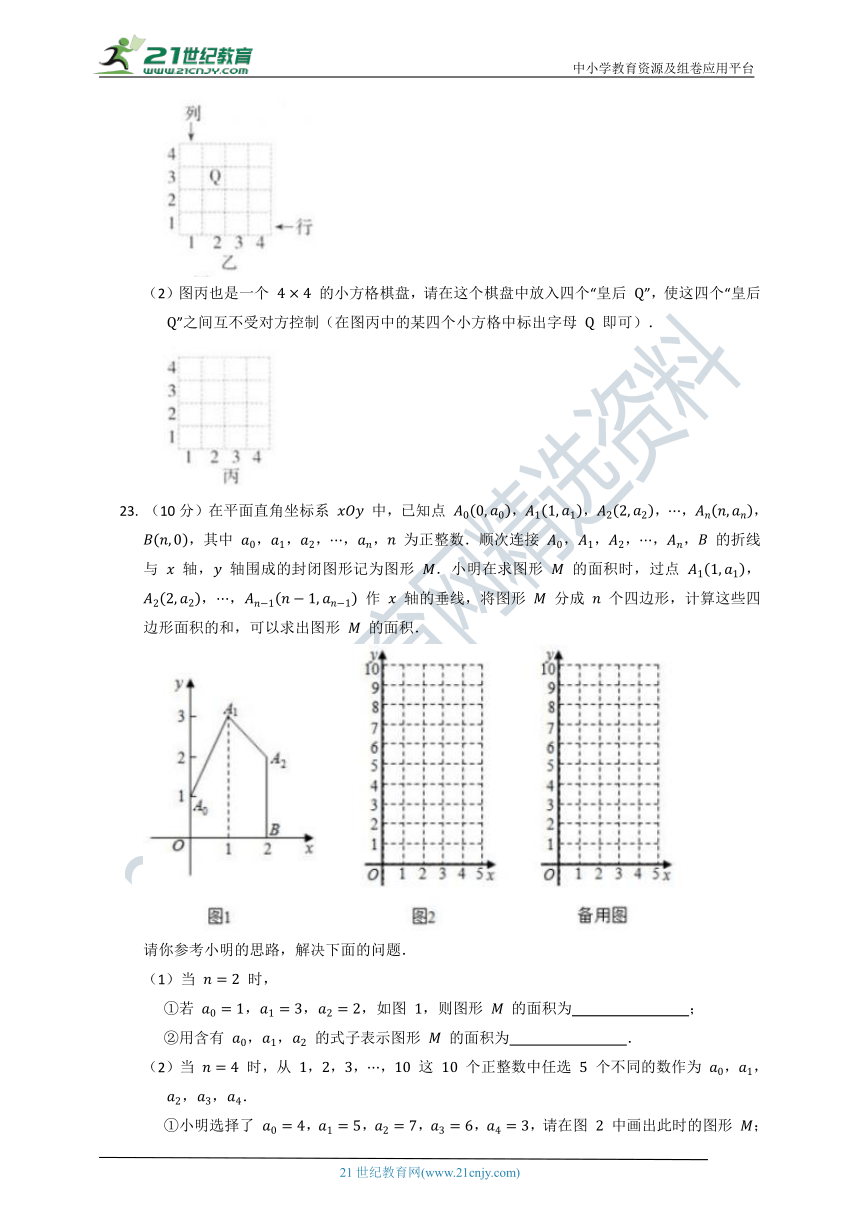
22.
(8分)国际象棋、中国象棋和围棋号称世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制它所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.图甲是一个
的小方格棋盘,图中的“皇后
”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后
”,它所在的位置可用“”来表示,请说明“皇后
”所在的位置“”的意义,并用这种表示法分别写出棋盘中不能被该“皇后
”所控制的四个位置;
(2)图丙也是一个
的小方格棋盘,请在这个棋盘中放入四个“皇后
”,使这四个“皇后
”之间互不受对方控制(在图丙中的某四个小方格中标出字母
即可).
23.
(10分)在平面直角坐标系
中,已知点
,,,,,,其中
,,,,,
为正整数.顺次连接
,,,,,
的折线与
轴,
轴围成的封闭图形记为图形
.小明在求图形
的面积时,过点
,,,
作
轴的垂线,将图形
分成
个四边形,计算这些四边形面积的和,可以求出图形
的面积.
请你参考小明的思路,解决下面的问题.
(1)当
时,
①若
,,,如图
,则图形
的面积为
;
②用含有
,,
的式子表示图形
的面积为
.
(2)当
时,从
,,,,
这
个正整数中任选
个不同的数作为
,,,,.
①小明选择了
,,,,,请在图
中画出此时的图形
;
②在①的条件下,若小聪用剩下的
个数
,,,,
作为
,,,,
的取值,使新得到的图形
的面积与小明的图形
的面积相等,请直接写出这五个数的排序
(写出一组即可).
24.
(8分)如图,在平面直角坐标系中,
三个顶点的坐标分别是
,,.
(1)画出
关于
轴对称的
;
(2)写出点
,,
的坐标
25.
(10分)在平面直角坐标系
中,对于
,
两点给出如下定义:若点
到
,
轴的距离中的最大值等于点
到
,
轴的距离中的最大值,则称
,
两点为“等距点”.图中的
,
两点即为“等距点”.
(1)已知点
的坐标为
,
①在点
,,
中,与点
为“等距点”的是
;
②若点
的坐标为
,且
,
两点为“等距点”,则点
的坐标为
;
(2)若
,
两点为“等距点”,求
的值.
答案
第一部分
1.
B
【解析】
点
关于
轴的对称点为
,
,,
点
为
,
故选B.
2.
C
【解析】
点
在
轴上方,
轴的左侧,
点
在第二象限,
又点
距离
轴
个单位长度,距离
轴
个单位长度,
点
的横坐标为
,纵坐标为
,故点
的坐标是
.
3.
C
【解析】“故宫”所在位置是
竖排,
横行;“鼓楼”所在的位置是
竖排,
横行.
故图中“故宫”“鼓楼”所在的区域分别是
,.
故选C.
4.
C
5.
D
6.
D
7.
D
【解析】A选项,云南西部,位置不确定,故本选项错误;
B选项,云南与缅甸交界处,位置不确定,故本选项错误;
C选项,东经
,位置不明确,故本选项错误;
D选项,东经
,北纬
,有序数对,位置明确,故本选项正确.故选D.
8.
B
9.
D
【解析】因为
在第二象限,
所以
,,即
,
所以
,,
所以点
在第四象限.
10.
D
【解析】①当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
,此结论正确;
②当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
,此结论正确;
③当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
,此结论正确;
④当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
,此结论正确.
11.
D
12.
C
【解析】,,点
在
轴上,
边上的高为
,
又
的面积为
,
,
易知点
在点
的左边或者右边,
点
的坐标为
或
.
故选C.
第二部分
13.
【解析】根据题意画出图形如图所示,
可得以点
为原点建立平面直角坐标系时,点
的坐标为
.
14.
排
列
15.
16.
或
17.
一、三
18.
,
【解析】【分析】根据已知两点坐标确定坐标系,然后确定其它点的位置.
【解析】解:由,两点的坐标分别为,,,,可知,坐标原点不在图中出现,是以线段的中垂线为轴,且向上为正方向,最下的水平线的纵坐标是2,以水平线为轴,且向右为正方向,
点的坐标为,.
故答案为:,.
【点评】解题的关键是确定坐标原点和,轴的位置及方向,或者直接利用坐标系中的移动法则右加左减,上加下减来确定坐标.
第三部分
19.
建立如图平面直角坐标系,敌军指挥部如图所示,即为点
.
20.
(1)
()如图,平面直角坐标系
即为所求.
()如图,
即为所求.
(2)
点
关于
轴对称的点的坐标为
.
21.
如图,建立平面直角坐标系,则
,,.(答案不唯一)
22.
(1)
“皇后
”所在的位置“”的意义:
位于棋盘中的第
列、第
行的位置;棋盘中不能被“皇后
”所控制的四个位置是
,,,.
(2)
答案不唯一,如图.
23.
(1)
①
;②
.
【解析】①如图
所示,
过点
,作
于
,
②同样可得图形
的面积
.
(2)
①如图
所示:
②
,,,,(答案不唯一)
【解析】②如图
所示,
小明的图形
的面积
,
新图形
的面积
.
新得到的图形
的面积与小明的图形
的面积相等.
24.
(1)
如图,
即为所求.
(2)
,,.
25.
(1)
,;
【解析】①
点
到
,
轴的距离中的最大值为
,
与点
是“等距点”的是点
,.
②当点
到
,
轴的距离中至少有一个为
时,点
的坐标有
,,,这些点中与
为“等距点”的是
.
(2)
,
两点为“等距点”,
①若
,则
或
,
解得
或
.
当
时,,故舍去;
当
时,,符合题意.
②若
,则
,
解得
或
.
当
时,,符合题意;
当
时,,故舍去.
综上可得,
的值是
或
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
北师大版2021-2022学年八年级(上)第三章位置与坐标检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共,36分)
1.
已知点
关于
轴的对称点是点
,那么点
为
A.
B.
C.
D.
2.
在平面直角坐标系中,点
在
轴上方,
轴的左侧,距离
轴
个单位长度,距离
轴
个单位长度,则点
的坐标为
A.
B.
C.
D.
3.
如图是某市地图简图的一部分,图中“故宫”“鼓楼”所在的区域分别是
A.
,
B.
,
C.
,
D.
,
4.
数学中有许多形状优美、寓意美好的曲线,曲线
就是其中之一(如图).给出下列三个结论:
①曲线
恰好经过
个整点(即横、纵坐标均为整数的点);
②曲线
在第一、二象限中的任意一点到原点的距离大于
;
③曲线
所围成的“心形”区域的面积小于
.
其中正确结论的序号是
A.
①
B.
②
C.
①②
D.
①②③
5.
在平面直角坐标系中,点
关于
轴对称的点的坐标为
A.
B.
C.
D.
6.
在平面直角坐标系中,点
位于
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
7.
年
月
日,云南省瑞丽市共增加
例新冠肺炎确诊病例,均为缅甸输入.下列表述中,能确定瑞丽市位置的是
A.
云南西部
B.
云南与缅甸交界处
C.
东经
D.
东经
,北纬
8.
若点
,
关于
轴对称,则
A.
,
B.
,
C.
,
D.
,
9.
若
在第二象限,则点
在第
象限.
A.
一
B.
二
C.
三
D.
四
10.
下图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为
轴、
轴的正方向建立平面直角坐标系.
有如下四个结论:
①当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
;
②当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
;
③当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
;
④当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
.
上述结论中,所有正确结论的序号是
A.
①②③
B.
②③④
C.
①④
D.
①②③④
11.
已知
和
两点,且
与坐标轴围成的三角形的面积等于
,则
的值为
A.
B.
C.
或
D.
或
12.
已知点
,,点
在
轴上,且
的面积为
,则点
的坐标为
A.
B.
C.
或
D.
无法确定
二、填空题(共6小题;每小题4分,共24分)
13.
在平面上有
,
两点,若以点
为原点建立平面直角坐标系,则点
坐标为
.若以点
为原点建立平面直角坐标系,则点
的坐标为
.
14.
七()班座位有
排
列,张艳的座位在
排
列,简记为
,班级座次表上写着王刚
,那么王刚的座位在
.
15.
若点
与点
关于
轴对称,则
的值是
.
16.
在平面直角坐标系
中,已知三角形的三个顶点的坐标分别是
,,,点
在
轴上,设三角形
和三角形
的面积分别为
和
,如果
,那么点
的纵坐标
的取值范围是
.
17.
已知点
是直角坐标平面内的点,若
,则点
在第
象限.
18.
如图,小强告诉小华图中,两点的坐标分别为,,,,小华一下就说出了在同一坐标系下的坐标
.
三、解答题(共7小题;共60分)
19.
(8分)如图是某战役缴获敌人防御工事坐标地图的碎片,依稀可见:一号暗堡
的坐标为
,五号暗堡
的坐标为
.另有情报得知敌军指挥部的坐标为
.请问你能找到敌军的指挥部吗
20.
(8分)在如图所示的正方形网格中,每个小正方形的边长都是
,
顶点都在网格线的交点上,点
的坐标为
,点
的坐标为
.
(1)()根据上述条件,在网格中建立平面直角坐标系
;
()画出
关于
轴对称的图形
;
(2)写出点
关于
轴对称的点的坐标.
21.(8分)
年
月
日新版《北京市生活垃圾管理条例》实施,意味着北京市垃圾分类正式进入法治化、常态化、系统化轨道.条例明确规定,将垃圾分为厨余垃圾、有害垃圾、其他垃圾和可回收物
类.为了帮助同学们养成垃圾分类的好习惯,七年级一班计划以此为主题召开一次班会,需要一部分同学手绘可回收物的标识小卡片(如图).发给大家的纸张和样图中的纸张一样,都是边长为
的正方形.为了让大家画的标志在纸张中的位置大小尽可能的一致.标志中标注了
,,
三个关键点,请你通过测量告诉大家
,,
三点在纸张中的位置.
22.
(8分)国际象棋、中国象棋和围棋号称世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制它所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.图甲是一个
的小方格棋盘,图中的“皇后
”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后
”,它所在的位置可用“”来表示,请说明“皇后
”所在的位置“”的意义,并用这种表示法分别写出棋盘中不能被该“皇后
”所控制的四个位置;
(2)图丙也是一个
的小方格棋盘,请在这个棋盘中放入四个“皇后
”,使这四个“皇后
”之间互不受对方控制(在图丙中的某四个小方格中标出字母
即可).
23.
(10分)在平面直角坐标系
中,已知点
,,,,,,其中
,,,,,
为正整数.顺次连接
,,,,,
的折线与
轴,
轴围成的封闭图形记为图形
.小明在求图形
的面积时,过点
,,,
作
轴的垂线,将图形
分成
个四边形,计算这些四边形面积的和,可以求出图形
的面积.
请你参考小明的思路,解决下面的问题.
(1)当
时,
①若
,,,如图
,则图形
的面积为
;
②用含有
,,
的式子表示图形
的面积为
.
(2)当
时,从
,,,,
这
个正整数中任选
个不同的数作为
,,,,.
①小明选择了
,,,,,请在图
中画出此时的图形
;
②在①的条件下,若小聪用剩下的
个数
,,,,
作为
,,,,
的取值,使新得到的图形
的面积与小明的图形
的面积相等,请直接写出这五个数的排序
(写出一组即可).
24.
(8分)如图,在平面直角坐标系中,
三个顶点的坐标分别是
,,.
(1)画出
关于
轴对称的
;
(2)写出点
,,
的坐标
25.
(10分)在平面直角坐标系
中,对于
,
两点给出如下定义:若点
到
,
轴的距离中的最大值等于点
到
,
轴的距离中的最大值,则称
,
两点为“等距点”.图中的
,
两点即为“等距点”.
(1)已知点
的坐标为
,
①在点
,,
中,与点
为“等距点”的是
;
②若点
的坐标为
,且
,
两点为“等距点”,则点
的坐标为
;
(2)若
,
两点为“等距点”,求
的值.
答案
第一部分
1.
B
【解析】
点
关于
轴的对称点为
,
,,
点
为
,
故选B.
2.
C
【解析】
点
在
轴上方,
轴的左侧,
点
在第二象限,
又点
距离
轴
个单位长度,距离
轴
个单位长度,
点
的横坐标为
,纵坐标为
,故点
的坐标是
.
3.
C
【解析】“故宫”所在位置是
竖排,
横行;“鼓楼”所在的位置是
竖排,
横行.
故图中“故宫”“鼓楼”所在的区域分别是
,.
故选C.
4.
C
5.
D
6.
D
7.
D
【解析】A选项,云南西部,位置不确定,故本选项错误;
B选项,云南与缅甸交界处,位置不确定,故本选项错误;
C选项,东经
,位置不明确,故本选项错误;
D选项,东经
,北纬
,有序数对,位置明确,故本选项正确.故选D.
8.
B
9.
D
【解析】因为
在第二象限,
所以
,,即
,
所以
,,
所以点
在第四象限.
10.
D
【解析】①当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
,此结论正确;
②当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
,此结论正确;
③当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
,此结论正确;
④当表示天安门的点的坐标为
,表示广安门的点的坐标为
时,表示左安门的点的坐标为
,此结论正确.
11.
D
12.
C
【解析】,,点
在
轴上,
边上的高为
,
又
的面积为
,
,
易知点
在点
的左边或者右边,
点
的坐标为
或
.
故选C.
第二部分
13.
【解析】根据题意画出图形如图所示,
可得以点
为原点建立平面直角坐标系时,点
的坐标为
.
14.
排
列
15.
16.
或
17.
一、三
18.
,
【解析】【分析】根据已知两点坐标确定坐标系,然后确定其它点的位置.
【解析】解:由,两点的坐标分别为,,,,可知,坐标原点不在图中出现,是以线段的中垂线为轴,且向上为正方向,最下的水平线的纵坐标是2,以水平线为轴,且向右为正方向,
点的坐标为,.
故答案为:,.
【点评】解题的关键是确定坐标原点和,轴的位置及方向,或者直接利用坐标系中的移动法则右加左减,上加下减来确定坐标.
第三部分
19.
建立如图平面直角坐标系,敌军指挥部如图所示,即为点
.
20.
(1)
()如图,平面直角坐标系
即为所求.
()如图,
即为所求.
(2)
点
关于
轴对称的点的坐标为
.
21.
如图,建立平面直角坐标系,则
,,.(答案不唯一)
22.
(1)
“皇后
”所在的位置“”的意义:
位于棋盘中的第
列、第
行的位置;棋盘中不能被“皇后
”所控制的四个位置是
,,,.
(2)
答案不唯一,如图.
23.
(1)
①
;②
.
【解析】①如图
所示,
过点
,作
于
,
②同样可得图形
的面积
.
(2)
①如图
所示:
②
,,,,(答案不唯一)
【解析】②如图
所示,
小明的图形
的面积
,
新图形
的面积
.
新得到的图形
的面积与小明的图形
的面积相等.
24.
(1)
如图,
即为所求.
(2)
,,.
25.
(1)
,;
【解析】①
点
到
,
轴的距离中的最大值为
,
与点
是“等距点”的是点
,.
②当点
到
,
轴的距离中至少有一个为
时,点
的坐标有
,,,这些点中与
为“等距点”的是
.
(2)
,
两点为“等距点”,
①若
,则
或
,
解得
或
.
当
时,,故舍去;
当
时,,符合题意.
②若
,则
,
解得
或
.
当
时,,符合题意;
当
时,,故舍去.
综上可得,
的值是
或
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
