22.3实际问题与二次函数同步提升训练 2021-2022学年人教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 22.3实际问题与二次函数同步提升训练 2021-2022学年人教版九年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 199.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 10:41:19 | ||
图片预览


文档简介
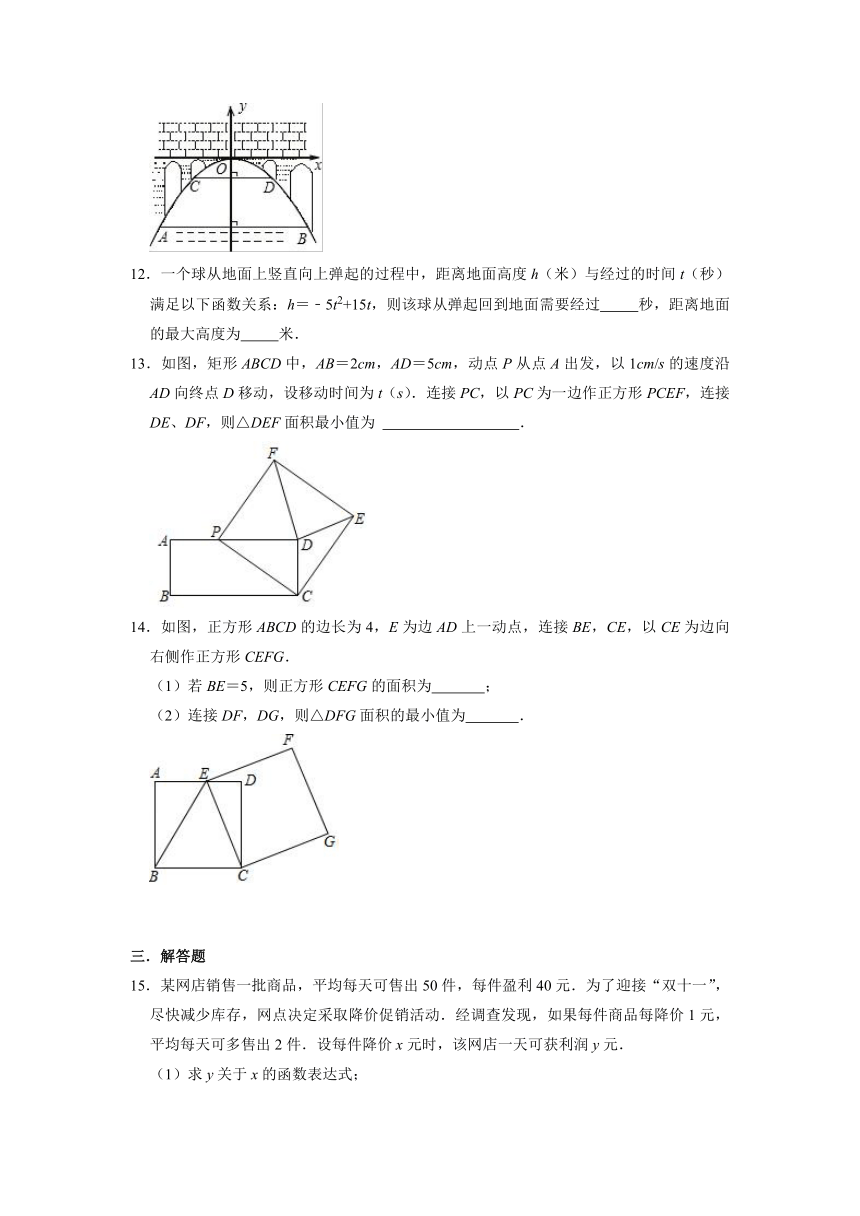
2021-2022学年人教版九年级数学上册《22.3实际问题与二次函数》同步提升训练(附答案)
一.选择题
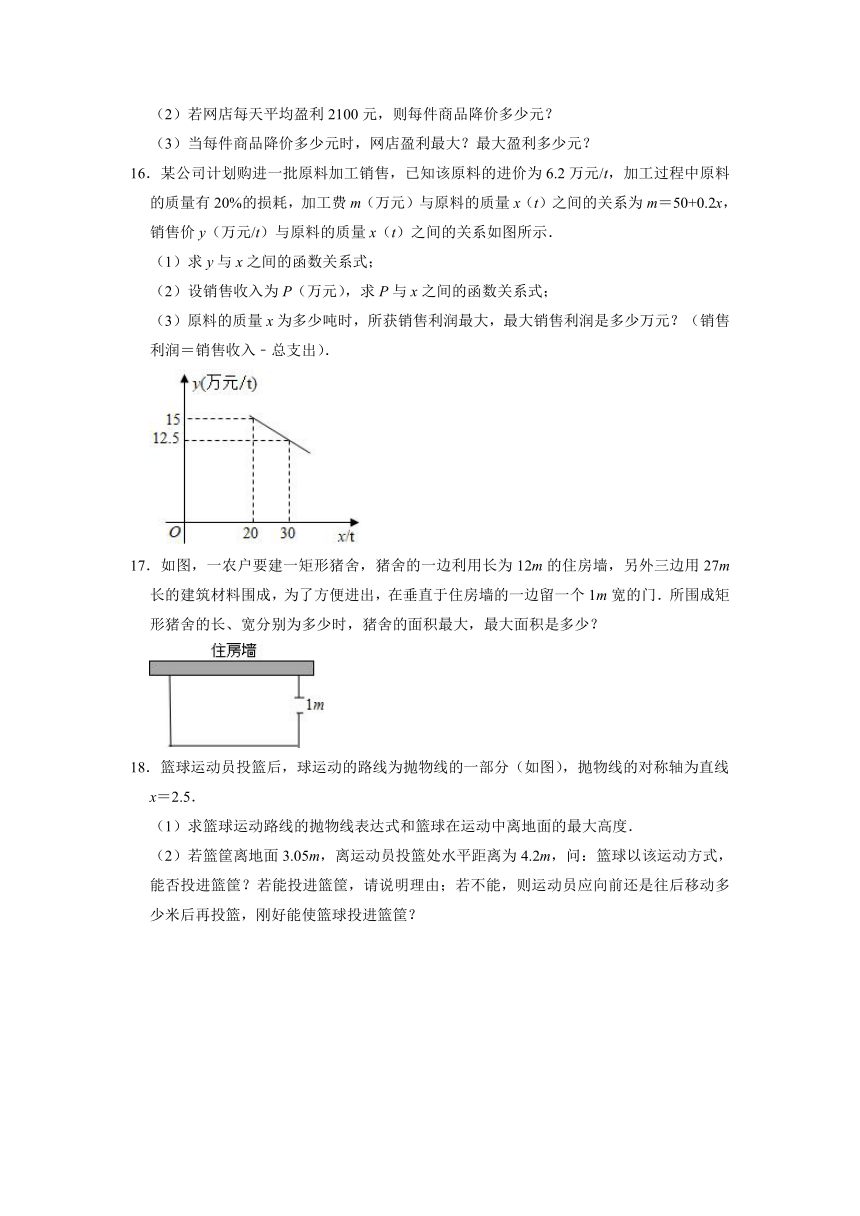
1.某商品的进价为每件60元,现在的售价为每件80元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=200﹣10x
B.y=(200﹣10x)(80﹣60﹣x)
C.y=(200+10x)(80﹣60﹣x)
D.y=(200﹣10x)(80﹣60+x)
2.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
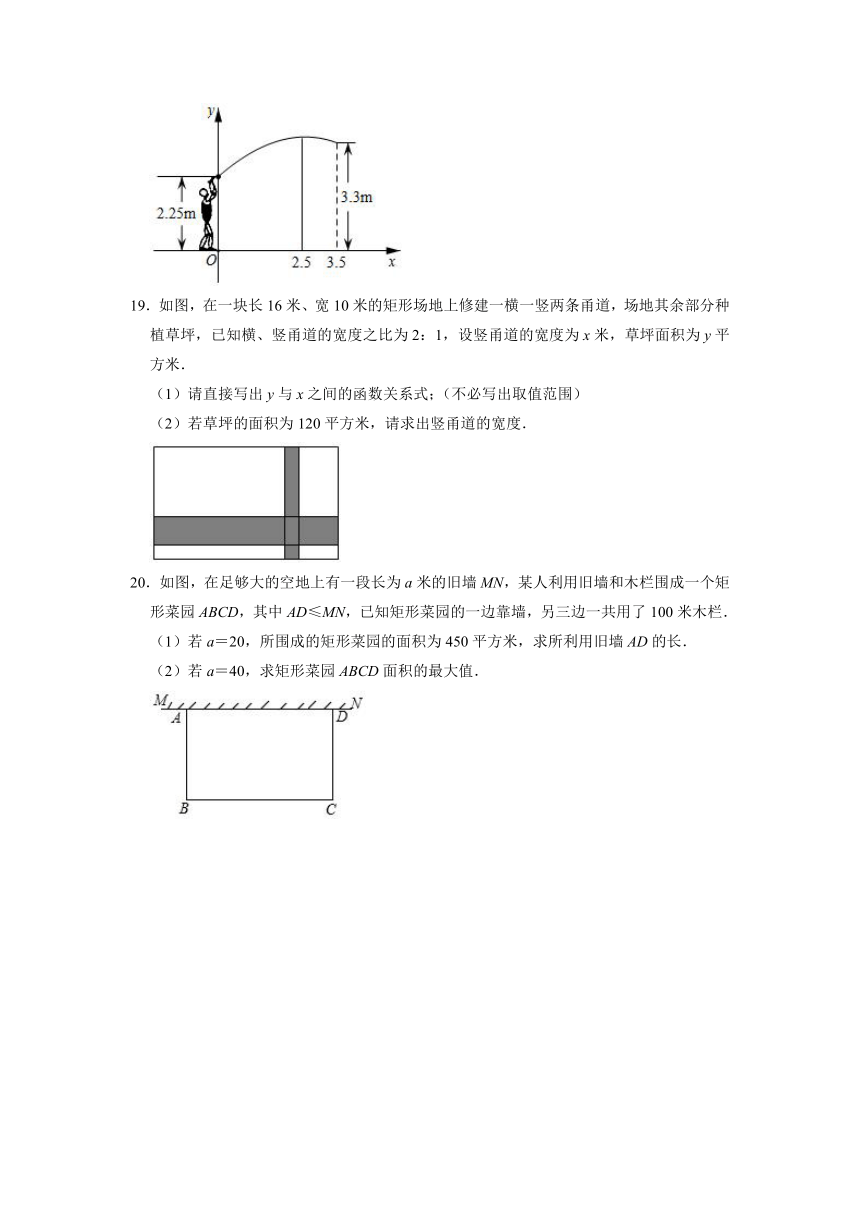
A.60
B.65
C.70
D.75
3.正方形ABCD中,AB=4,P为对角线BD上一动点,F为射线AD上一点,若AP=PF,则△APF的面积最大值为( )
A.8
B.6
C.4
D.2
4.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列四个结论:其中正确结论的个数是( )
①图象具有对称性,对称轴是直线x=1;②当﹣1<x<1或x>3时,函数值随x值的增大而增大;③当x=﹣1或x=3时,函数的最小值是0;④当x=1时,函数的最大值是4.
A.4
B.3
C.2
D.1
5.如图,小明以抛物线y=x2﹣2x+4为灵感设计了一款杯子,若AB=4,DE=2,则杯子的高CE为( )
A.4
B.5
C.6
D.7
6.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从A开始沿边AB向点B以1cm/s的速度移动,动点Q从B开始沿边BC向点C以2cm/s的速度移动,如果P、Q两点分别从A、B两点同时出发,则四边形APQC的面积的最小值是( )
A.9
B.18
C.27
D.36
二.填空题
7.二次函数y=x2﹣2x﹣3(3≤x≤6)的最小值是
.
8.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为
元时,才能使每天所获销售利润最大.
9.如图,P是抛物线y=x2﹣2x﹣3在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为
.
10.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=﹣2x2+4x+1,则喷出水珠的最大高度是
m.
11.如图,有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升,则再持续
小时水位才能到拱桥顶.
12.一个球从地面上竖直向上弹起的过程中,距离地面高度h(米)与经过的时间t(秒)满足以下函数关系:h=﹣5t2+15t,则该球从弹起回到地面需要经过
秒,距离地面的最大高度为
米.
13.如图,矩形ABCD中,AB=2cm,AD=5cm,动点P从点A出发,以1cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则△DEF面积最小值为
.
14.如图,正方形ABCD的边长为4,E为边AD上一动点,连接BE,CE,以CE为边向右侧作正方形CEFG.
(1)若BE=5,则正方形CEFG的面积为
;
(2)连接DF,DG,则△DFG面积的最小值为
.
三.解答题
15.某网店销售一批商品,平均每天可售出50件,每件盈利40元.为了迎接“双十一”,尽快减少库存,网点决定采取降价促销活动.经调查发现,如果每件商品每降价1元,平均每天可多售出2件.设每件降价x元时,该网店一天可获利润y元.
(1)求y关于x的函数表达式;
(2)若网店每天平均盈利2100元,则每件商品降价多少元?
(3)当每件商品降价多少元时,网店盈利最大?最大盈利多少元?
16.某公司计划购进一批原料加工销售,已知该原料的进价为6.2万元/t,加工过程中原料的质量有20%的损耗,加工费m(万元)与原料的质量x(t)之间的关系为m=50+0.2x,销售价y(万元/t)与原料的质量x(t)之间的关系如图所示.
(1)求y与x之间的函数关系式;
(2)设销售收入为P(万元),求P与x之间的函数关系式;
(3)原料的质量x为多少吨时,所获销售利润最大,最大销售利润是多少万元?(销售利润=销售收入﹣总支出).
17.如图,一农户要建一矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用27m长的建筑材料围成,为了方便进出,在垂直于住房墙的一边留一个1m宽的门.所围成矩形猪舍的长、宽分别为多少时,猪舍的面积最大,最大面积是多少?
18.篮球运动员投篮后,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为直线x=2.5.
(1)求篮球运动路线的抛物线表达式和篮球在运动中离地面的最大高度.
(2)若篮筐离地面3.05m,离运动员投篮处水平距离为4.2m,问:篮球以该运动方式,能否投进篮筐?若能投进篮筐,请说明理由;若不能,则运动员应向前还是往后移动多少米后再投篮,刚好能使篮球投进篮筐?
19.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为x米,草坪面积为y平方米.
(1)请直接写出y与x之间的函数关系式;(不必写出取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
20.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长.
(2)若a=40,求矩形菜园ABCD面积的最大值.
参考答案
1.解:∵每涨价1元,每星期要少卖出10件,每件涨价x元,
∴销售每件的利润为(80﹣60+x)元,每星期的销售量为(200﹣10x),
∴每星期售出商品的利润y=(200﹣10x)(80﹣60+x).
故选:D.
2.解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
3.解:作PM⊥AD与M,
∵BD是正方形ABCD的对角线,
∴∠ADB=45°,
∴△BDM是等腰直角三角形,
∴PM=DM,
设PM=DM=x,则AM=4﹣x,
∵AP=PF,
∴AM=FM=4﹣x,
∴AF=2(4﹣x),
∵S△APF=AF PM,
∴S△APF=×2(4﹣x) x=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,S△APF有最大值4,
故选:C.
4.解:观察图象可知,图象具有对称性,对称轴是直线x=﹣=1,故①正确;
令|x2﹣2x﹣3|=0可得x2﹣2x﹣3=0,
∴(x+1)(x﹣3)=0,
∴x1=﹣1,x2=3,
∴(﹣1,0)和(3,0)是函数图象与x轴的交点坐标,
又对称轴是直线x=1,
∴当﹣1<x<1或x>3时,函数值y随x值的增大而增大,故②正确;
由图象可知(﹣1,0)和(3,0)是函数图象的最低点,则当x=﹣1或x=3时,函数最小值是0,故③正确;
由图象可知,当x<﹣1时,函数值随x的减小而增大,当x>3时,函数值随x的增大而增大,均存在大于顶点坐标的函数值,
故当x=1时的函数值4并非最大值,故④错误.
综上,只有④错误.
故选:B.
5.解:∵y=x2﹣2x+4
=(x﹣1)2+3,
∴抛物线的顶点D的坐标为(1,3),
∵AB=4,
∴BC=2,
∴点B的横坐标为x=3,
把x=3代入y=x2﹣2x+4得y=7,
∴CD=7﹣3=4,
∴CE=CE+DE=4+2=6,
故选:C.
6.解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC﹣S△PBQ
=×12×6﹣(6﹣t)×2t
=t2﹣6t+36
=(t﹣3)2+27.
∴当t=3s时,S取得最小值为27.
故选:C.
7.解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴对称轴为x=1,
∵3≤x≤6时,y随x的增大而增大,
∴x=3时,有最小值,y最小值=22﹣4=0;
故答案为:0.
8.解:设销售单价定为x元(x≥9),每天所获利润为y元,
则y=[20﹣4(x﹣9)] (x﹣8)
=﹣4x2+88x﹣448
=﹣4(x﹣11)2+36,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
故答案为11.
9.解:设P(x,x2﹣2x3),
∵过点P分别向x轴和y轴作垂线,垂足分别为A、B,
∴四边形OAPB为矩形,
∴四边形OAPB周长=2PA+2OA
=﹣2(x2﹣2x﹣3)+2x
=﹣2x2+6x+6
=﹣2(x2﹣3x)+6,
=﹣2+.
∴当x=时,四边形OAPB周长有最大值,最大值为.
故答案为.
10.解:∵y=﹣2x2+4x+1=﹣2(x﹣1)2+3,
∴当x=1时,y有最大值为3,
∴喷出水珠的最大高度是3m,
故答案为:3.
11.解:设抛物线的解析式为y=ax2,
设D(5,b),则B(10,b﹣3),
把D、B的坐标分别代入y=ax2得:
,
解得,
∴y=﹣x2;
∵b=﹣1,
∴拱桥顶O到CD的距离为1,
1÷0.2=5(小时).
所以再持续5小时到达拱桥顶.
故答案为:5.
12.解:当该球从弹起回到地面时h=0,
∴0=﹣5t2+15t,
解得:t1=0或t2=3,
t=0时小球还未离开地面,
∴t=3时小球从弹起回到地面;
∵h=﹣5t2+15t=﹣5(t﹣)2+,﹣5<0,
∴当t=时,h取得最大值;
故答案为:3,.
13.解:设△PCD的面积为y,
由题意得:AP=t,PD=5﹣t,
∴y==5﹣t,
∵四边形EFPC是正方形,
∴S△DEF+S△PDC=S正方形EFPC,
∵PC2=PD2+CD2,
∴PC2=22+(5﹣t)2=t2﹣10t+29,
∴S△DEF=(t2﹣10t+29)﹣(5﹣t)=t2﹣4t+=(t﹣4)2+,
当t为4时,△DEF的面积最小,且最小值为.
故答案为:.
14.解:(1)∵四边形ABCD是正方形,
∴AB=AD=4,∠A=∠ADC=90°,
∵BE=5,
∴AE===3,
∴DE=AD﹣AE=4﹣3=1,
∴EC2=DE2+CD2=12+42=17,
∴正方形CEFG的面积=EC2=17.
故答案为17.
(2)连接DF,DG.设DE=x,则CE=,
∵S△DEC+S△DFG=S正方形ECGF,
∴S△DFG=(x2+16)﹣×x×4=x2﹣2x+8=(x﹣2)2+6,
∵>0,
∴x=2时,△DFG的面积的最小值为6.
故答案为6.
15.解:(1)每件降价x元时,每件盈利(40﹣x)元,每天可售出(50+2x)件,则该网店一天可获利润为
y=(40﹣x)(50+2x)=﹣2x2+30x+2000;
(2)当y=2100时,﹣2x2+30x+2000=2100,
解得:x1=10,x2=5,
∵尽快减少库存,降价越多越好,
∴x=10,
答:每天盈利2100元,需降价10元.
(3)y=﹣2x2+30x+2000=,
∵a=﹣2<0,
∴当x=7.5,ymax=2112.5(元).
答:每件商品降价7.5元时,可获得最大利润2112.5元.
16.解:(1)设y与x之间的函数关系式为y=kx+b,
将(20,15),(30,12.5)代入,
可得:,
解得:,
∴y与x之间的函数关系式为y=﹣x+20;
(2)设销售收入为P(万元),
∴P=(1﹣20%)xy=(﹣x+20)x=﹣x2+16x,
∴P与x之间的函数关系式为P=﹣x2+16x;
(3)设销售总利润为W(万元),
∴W=P﹣6.2x﹣m=﹣x2+16x﹣6.2x﹣(50+0.2x),
整理,可得:W=﹣x2+x﹣50,
W=﹣(x﹣24)2+65.2,
∵﹣<0,
∴当x=24时,W有最大值为65.2,
∴原料的质量为24吨时,所获销售利润最大,最大销售利润是65.2万元.
17.解:设矩形猪舍垂直于住房墙一边长为xm,可以得出平行于墙的一边的长为(27﹣2x+1)m,
由题意得y=x(27﹣2x+1)=﹣2(x﹣7)2+98,对称轴为x=7,
∵27﹣2x+1≤12,27﹣2x+1>0,
∴8≤x<14,
在y=﹣2(x﹣7)2+98中,﹣2<0,在对称轴右侧y随着x的增大而减小,
所以当x=8m时,矩形猪舍的长为27﹣2x+1=12(m),宽为8m时,猪舍的面积最大,最大面积是96平方米.
答:矩形猪舍的长、宽分别为12m、8m时,猪舍的面积最大,最大面积是96平方米.
18.解:(1)设抛物线的解析式为y=a(x﹣2.5)2+h,
将(0,2.25)和(3.5,3.3)代入,得:
,
解得:,
∴抛物线的解析式为y=﹣0.2(x﹣2.5)2+3.5,(0≤x≤3.5),
当x=2.5时,y最大,最大值为3.5m,
∴篮球在运动中离地面的最大高度为3.5m;
(2)不能,
∵篮筐离地面3.05m,
∴3.05=﹣0.2(x﹣2.5)2+3.5,
解得:x1=1,x2=4,
∴抛物线向右平移0.2m,即运动员应向前移动0.2m,
19.解:(1)设竖甬道的宽度为x米,草坪面积为y平方米,则横甬道的宽度为2x米,剩余部分可合成长(16﹣x)米,宽(10﹣2x)米的矩形,
依题意得:y=(16﹣x)(10﹣2x)=2x2﹣42x+160.
(2)依题意得:2x2﹣42x+160=120,
整理得:x2﹣21x+20=0,
解得:x1=1,x2=20.
当x=1时,10﹣2x=10﹣2×1=8>0,符合题意;
当x=20时,10﹣2x=10﹣2×20=﹣30<0,不符合题意,舍去.
答:竖甬道的宽度为1米.
20.解:(1)设AB=xm,则BC=(100﹣2x)m,
根据题意得x(100﹣2x)=450,
解得x1=5,x2=45,
当x=5时,100﹣2x=90>20,不合题意舍去;
当x=45时,100﹣2x=10,
答:AD的长为10m;
(2)设AD=xm.
∴S=x(100﹣x)=﹣(x﹣50)2+1250,
∵a=40,
∴x=40时,S的最大值为:﹣(40﹣50)2+1250=﹣50+1250=1200(m ).
答:若a=40,矩形菜园ABCD面积的最大值为1200平方米.
一.选择题
1.某商品的进价为每件60元,现在的售价为每件80元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=200﹣10x
B.y=(200﹣10x)(80﹣60﹣x)
C.y=(200+10x)(80﹣60﹣x)
D.y=(200﹣10x)(80﹣60+x)
2.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60
B.65
C.70
D.75
3.正方形ABCD中,AB=4,P为对角线BD上一动点,F为射线AD上一点,若AP=PF,则△APF的面积最大值为( )
A.8
B.6
C.4
D.2
4.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列四个结论:其中正确结论的个数是( )
①图象具有对称性,对称轴是直线x=1;②当﹣1<x<1或x>3时,函数值随x值的增大而增大;③当x=﹣1或x=3时,函数的最小值是0;④当x=1时,函数的最大值是4.
A.4
B.3
C.2
D.1
5.如图,小明以抛物线y=x2﹣2x+4为灵感设计了一款杯子,若AB=4,DE=2,则杯子的高CE为( )
A.4
B.5
C.6
D.7
6.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从A开始沿边AB向点B以1cm/s的速度移动,动点Q从B开始沿边BC向点C以2cm/s的速度移动,如果P、Q两点分别从A、B两点同时出发,则四边形APQC的面积的最小值是( )
A.9
B.18
C.27
D.36
二.填空题
7.二次函数y=x2﹣2x﹣3(3≤x≤6)的最小值是
.
8.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为
元时,才能使每天所获销售利润最大.
9.如图,P是抛物线y=x2﹣2x﹣3在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为
.
10.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=﹣2x2+4x+1,则喷出水珠的最大高度是
m.
11.如图,有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升,则再持续
小时水位才能到拱桥顶.
12.一个球从地面上竖直向上弹起的过程中,距离地面高度h(米)与经过的时间t(秒)满足以下函数关系:h=﹣5t2+15t,则该球从弹起回到地面需要经过
秒,距离地面的最大高度为
米.
13.如图,矩形ABCD中,AB=2cm,AD=5cm,动点P从点A出发,以1cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则△DEF面积最小值为
.
14.如图,正方形ABCD的边长为4,E为边AD上一动点,连接BE,CE,以CE为边向右侧作正方形CEFG.
(1)若BE=5,则正方形CEFG的面积为
;
(2)连接DF,DG,则△DFG面积的最小值为
.
三.解答题
15.某网店销售一批商品,平均每天可售出50件,每件盈利40元.为了迎接“双十一”,尽快减少库存,网点决定采取降价促销活动.经调查发现,如果每件商品每降价1元,平均每天可多售出2件.设每件降价x元时,该网店一天可获利润y元.
(1)求y关于x的函数表达式;
(2)若网店每天平均盈利2100元,则每件商品降价多少元?
(3)当每件商品降价多少元时,网店盈利最大?最大盈利多少元?
16.某公司计划购进一批原料加工销售,已知该原料的进价为6.2万元/t,加工过程中原料的质量有20%的损耗,加工费m(万元)与原料的质量x(t)之间的关系为m=50+0.2x,销售价y(万元/t)与原料的质量x(t)之间的关系如图所示.
(1)求y与x之间的函数关系式;
(2)设销售收入为P(万元),求P与x之间的函数关系式;
(3)原料的质量x为多少吨时,所获销售利润最大,最大销售利润是多少万元?(销售利润=销售收入﹣总支出).
17.如图,一农户要建一矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用27m长的建筑材料围成,为了方便进出,在垂直于住房墙的一边留一个1m宽的门.所围成矩形猪舍的长、宽分别为多少时,猪舍的面积最大,最大面积是多少?
18.篮球运动员投篮后,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为直线x=2.5.
(1)求篮球运动路线的抛物线表达式和篮球在运动中离地面的最大高度.
(2)若篮筐离地面3.05m,离运动员投篮处水平距离为4.2m,问:篮球以该运动方式,能否投进篮筐?若能投进篮筐,请说明理由;若不能,则运动员应向前还是往后移动多少米后再投篮,刚好能使篮球投进篮筐?
19.如图,在一块长16米、宽10米的矩形场地上修建一横一竖两条甬道,场地其余部分种植草坪,已知横、竖甬道的宽度之比为2:1,设竖甬道的宽度为x米,草坪面积为y平方米.
(1)请直接写出y与x之间的函数关系式;(不必写出取值范围)
(2)若草坪的面积为120平方米,请求出竖甬道的宽度.
20.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长.
(2)若a=40,求矩形菜园ABCD面积的最大值.
参考答案
1.解:∵每涨价1元,每星期要少卖出10件,每件涨价x元,
∴销售每件的利润为(80﹣60+x)元,每星期的销售量为(200﹣10x),
∴每星期售出商品的利润y=(200﹣10x)(80﹣60+x).
故选:D.
2.解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
3.解:作PM⊥AD与M,
∵BD是正方形ABCD的对角线,
∴∠ADB=45°,
∴△BDM是等腰直角三角形,
∴PM=DM,
设PM=DM=x,则AM=4﹣x,
∵AP=PF,
∴AM=FM=4﹣x,
∴AF=2(4﹣x),
∵S△APF=AF PM,
∴S△APF=×2(4﹣x) x=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,S△APF有最大值4,
故选:C.
4.解:观察图象可知,图象具有对称性,对称轴是直线x=﹣=1,故①正确;
令|x2﹣2x﹣3|=0可得x2﹣2x﹣3=0,
∴(x+1)(x﹣3)=0,
∴x1=﹣1,x2=3,
∴(﹣1,0)和(3,0)是函数图象与x轴的交点坐标,
又对称轴是直线x=1,
∴当﹣1<x<1或x>3时,函数值y随x值的增大而增大,故②正确;
由图象可知(﹣1,0)和(3,0)是函数图象的最低点,则当x=﹣1或x=3时,函数最小值是0,故③正确;
由图象可知,当x<﹣1时,函数值随x的减小而增大,当x>3时,函数值随x的增大而增大,均存在大于顶点坐标的函数值,
故当x=1时的函数值4并非最大值,故④错误.
综上,只有④错误.
故选:B.
5.解:∵y=x2﹣2x+4
=(x﹣1)2+3,
∴抛物线的顶点D的坐标为(1,3),
∵AB=4,
∴BC=2,
∴点B的横坐标为x=3,
把x=3代入y=x2﹣2x+4得y=7,
∴CD=7﹣3=4,
∴CE=CE+DE=4+2=6,
故选:C.
6.解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC﹣S△PBQ
=×12×6﹣(6﹣t)×2t
=t2﹣6t+36
=(t﹣3)2+27.
∴当t=3s时,S取得最小值为27.
故选:C.
7.解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴对称轴为x=1,
∵3≤x≤6时,y随x的增大而增大,
∴x=3时,有最小值,y最小值=22﹣4=0;
故答案为:0.
8.解:设销售单价定为x元(x≥9),每天所获利润为y元,
则y=[20﹣4(x﹣9)] (x﹣8)
=﹣4x2+88x﹣448
=﹣4(x﹣11)2+36,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
故答案为11.
9.解:设P(x,x2﹣2x3),
∵过点P分别向x轴和y轴作垂线,垂足分别为A、B,
∴四边形OAPB为矩形,
∴四边形OAPB周长=2PA+2OA
=﹣2(x2﹣2x﹣3)+2x
=﹣2x2+6x+6
=﹣2(x2﹣3x)+6,
=﹣2+.
∴当x=时,四边形OAPB周长有最大值,最大值为.
故答案为.
10.解:∵y=﹣2x2+4x+1=﹣2(x﹣1)2+3,
∴当x=1时,y有最大值为3,
∴喷出水珠的最大高度是3m,
故答案为:3.
11.解:设抛物线的解析式为y=ax2,
设D(5,b),则B(10,b﹣3),
把D、B的坐标分别代入y=ax2得:
,
解得,
∴y=﹣x2;
∵b=﹣1,
∴拱桥顶O到CD的距离为1,
1÷0.2=5(小时).
所以再持续5小时到达拱桥顶.
故答案为:5.
12.解:当该球从弹起回到地面时h=0,
∴0=﹣5t2+15t,
解得:t1=0或t2=3,
t=0时小球还未离开地面,
∴t=3时小球从弹起回到地面;
∵h=﹣5t2+15t=﹣5(t﹣)2+,﹣5<0,
∴当t=时,h取得最大值;
故答案为:3,.
13.解:设△PCD的面积为y,
由题意得:AP=t,PD=5﹣t,
∴y==5﹣t,
∵四边形EFPC是正方形,
∴S△DEF+S△PDC=S正方形EFPC,
∵PC2=PD2+CD2,
∴PC2=22+(5﹣t)2=t2﹣10t+29,
∴S△DEF=(t2﹣10t+29)﹣(5﹣t)=t2﹣4t+=(t﹣4)2+,
当t为4时,△DEF的面积最小,且最小值为.
故答案为:.
14.解:(1)∵四边形ABCD是正方形,
∴AB=AD=4,∠A=∠ADC=90°,
∵BE=5,
∴AE===3,
∴DE=AD﹣AE=4﹣3=1,
∴EC2=DE2+CD2=12+42=17,
∴正方形CEFG的面积=EC2=17.
故答案为17.
(2)连接DF,DG.设DE=x,则CE=,
∵S△DEC+S△DFG=S正方形ECGF,
∴S△DFG=(x2+16)﹣×x×4=x2﹣2x+8=(x﹣2)2+6,
∵>0,
∴x=2时,△DFG的面积的最小值为6.
故答案为6.
15.解:(1)每件降价x元时,每件盈利(40﹣x)元,每天可售出(50+2x)件,则该网店一天可获利润为
y=(40﹣x)(50+2x)=﹣2x2+30x+2000;
(2)当y=2100时,﹣2x2+30x+2000=2100,
解得:x1=10,x2=5,
∵尽快减少库存,降价越多越好,
∴x=10,
答:每天盈利2100元,需降价10元.
(3)y=﹣2x2+30x+2000=,
∵a=﹣2<0,
∴当x=7.5,ymax=2112.5(元).
答:每件商品降价7.5元时,可获得最大利润2112.5元.
16.解:(1)设y与x之间的函数关系式为y=kx+b,
将(20,15),(30,12.5)代入,
可得:,
解得:,
∴y与x之间的函数关系式为y=﹣x+20;
(2)设销售收入为P(万元),
∴P=(1﹣20%)xy=(﹣x+20)x=﹣x2+16x,
∴P与x之间的函数关系式为P=﹣x2+16x;
(3)设销售总利润为W(万元),
∴W=P﹣6.2x﹣m=﹣x2+16x﹣6.2x﹣(50+0.2x),
整理,可得:W=﹣x2+x﹣50,
W=﹣(x﹣24)2+65.2,
∵﹣<0,
∴当x=24时,W有最大值为65.2,
∴原料的质量为24吨时,所获销售利润最大,最大销售利润是65.2万元.
17.解:设矩形猪舍垂直于住房墙一边长为xm,可以得出平行于墙的一边的长为(27﹣2x+1)m,
由题意得y=x(27﹣2x+1)=﹣2(x﹣7)2+98,对称轴为x=7,
∵27﹣2x+1≤12,27﹣2x+1>0,
∴8≤x<14,
在y=﹣2(x﹣7)2+98中,﹣2<0,在对称轴右侧y随着x的增大而减小,
所以当x=8m时,矩形猪舍的长为27﹣2x+1=12(m),宽为8m时,猪舍的面积最大,最大面积是96平方米.
答:矩形猪舍的长、宽分别为12m、8m时,猪舍的面积最大,最大面积是96平方米.
18.解:(1)设抛物线的解析式为y=a(x﹣2.5)2+h,
将(0,2.25)和(3.5,3.3)代入,得:
,
解得:,
∴抛物线的解析式为y=﹣0.2(x﹣2.5)2+3.5,(0≤x≤3.5),
当x=2.5时,y最大,最大值为3.5m,
∴篮球在运动中离地面的最大高度为3.5m;
(2)不能,
∵篮筐离地面3.05m,
∴3.05=﹣0.2(x﹣2.5)2+3.5,
解得:x1=1,x2=4,
∴抛物线向右平移0.2m,即运动员应向前移动0.2m,
19.解:(1)设竖甬道的宽度为x米,草坪面积为y平方米,则横甬道的宽度为2x米,剩余部分可合成长(16﹣x)米,宽(10﹣2x)米的矩形,
依题意得:y=(16﹣x)(10﹣2x)=2x2﹣42x+160.
(2)依题意得:2x2﹣42x+160=120,
整理得:x2﹣21x+20=0,
解得:x1=1,x2=20.
当x=1时,10﹣2x=10﹣2×1=8>0,符合题意;
当x=20时,10﹣2x=10﹣2×20=﹣30<0,不符合题意,舍去.
答:竖甬道的宽度为1米.
20.解:(1)设AB=xm,则BC=(100﹣2x)m,
根据题意得x(100﹣2x)=450,
解得x1=5,x2=45,
当x=5时,100﹣2x=90>20,不合题意舍去;
当x=45时,100﹣2x=10,
答:AD的长为10m;
(2)设AD=xm.
∴S=x(100﹣x)=﹣(x﹣50)2+1250,
∵a=40,
∴x=40时,S的最大值为:﹣(40﹣50)2+1250=﹣50+1250=1200(m ).
答:若a=40,矩形菜园ABCD面积的最大值为1200平方米.
同课章节目录
