12.1全等三角形 同步能力提升训练 2021-2022学年八年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 12.1全等三角形 同步能力提升训练 2021-2022学年八年级数学人教版上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 199.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 10:52:13 | ||
图片预览




文档简介
2021-2022人教版八年级数学上册《12.1全等三角形》同步能力提升训练(附答案)
一.选择题
1.如果两个图形全等,那么这两个图形必定是( )
A.形状大小均相同
B.形状相同,但大小不同
C.大小相同,但形状不同
D.形状大小均不相同
2.若△ABC与△DEF全等,A和E,B和D分别是对应点,则下列结论错误的是( )
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF
3.全等三角形又叫做合同三角形.平面内的合同三角形分为真正合同三角形和镜面合同三角形.假如△ABC和△A′B′C′是全等三角形,且点A与点A′对应,点B与点B′对应,点C与点C′对应.当沿周界A﹣B﹣C﹣A及A′﹣B′﹣C′﹣A′环绕时,若运动方向相同,则称它们是真正合同三角形(如图①);若运动方向相反,则称它们是镜面合同三角形(如图②).
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个翻转180度.下列各组合同三角形中,属于镜面合同三角形的是( )
A.B.C.D.
4.△ABC≌△DEF,下列结论中不正确的是( )
A.AB=DE
B.BE=CF
C.BC=EF
D.AC=DE
5.如图,△ABC≌△ADE,点E在BC边上,∠AED=80°,则∠CAE的度数为( )
A.80°
B.60°
C.40°
D.20°
6.下列说法:①能够重合的两个图形一定是全等图形;②两个全等图形的面积一定相等;③两个面积相等的图形一定是全等图形;④两个周长相等的图形一定是全等图形.这些说法中正确的是( )
A.①②
B.②③④
C.①②④
D.①②③④
7.下列说法:①全等图形的形状相同、大小相等;②三边对应相等的两个三角形全等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )
A.①②④
B.①③④
C.②③④
D.①②③④
8.已知△ABC的边长均为整数,且最大边的边长为4,那么符合条件的不全等的三角形最多有( )
A.4个
B.5个
C.6个
D.7个
9.如图,△ABC≌△DEC,点E在边AB上,∠DEC=75°,则∠BCE的度数是( )
A.25°
B.30°
C.40°
D.75°
二.填空题
10.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=
°.
11.在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为
.
如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有
.
13.已知△ABC≌△DEF,若AB=5,则DE=
.
14.已知△ABC≌△DEF,且△ABC的三边长分别为3cm,4cm,5cm,则△DEF的周长为
cm.
15.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2=
度.
16.如图,把一张长方形纸板裁去两个边长为3cm的小正方形和两个全等的小长方形,再把剩余部分(阴影部分)四周折起,恰好做成一个有底有盖的长方体纸盒,纸盒底面长方形的长为3kcm,宽为2kcm,则:
(1)裁去的每个小长方形面积为
cm2.(用k的代数式表示)
(2)若长方体纸盒的表面积是底面积的正整数倍,则正整数k的值为
.
17.如图AB,CD相交于点E,若△ABC≌△ADE,∠BAC=28°,则∠B的度数是
.
18.如图,△ABC中,点D、点E分别在边AB、BC上,连结AE、DE,若△ADE≌△BDE,AC:AB:BC=2:3:4,且△ABC的周长比△AEC的周长大6.则△AEC的周长为
.
三.解答题
19.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.
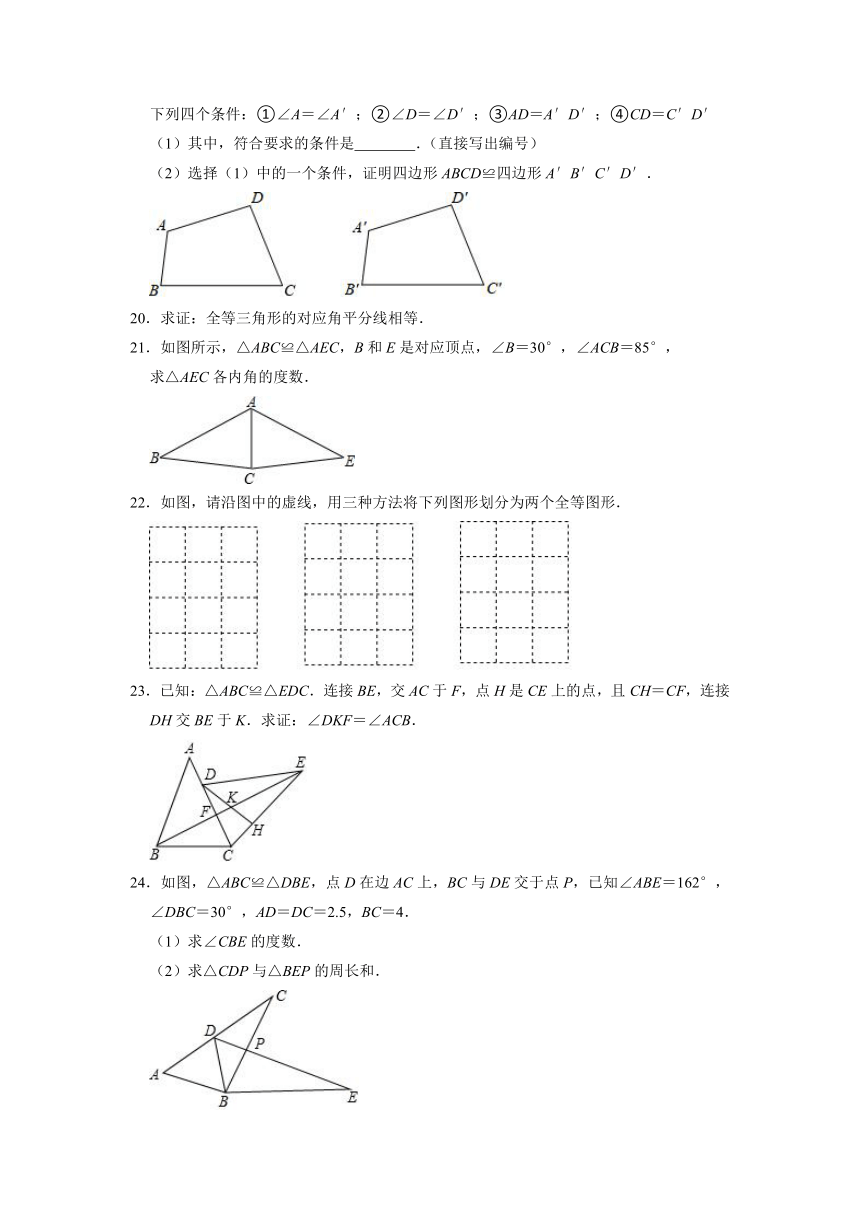
如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.
下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′
(1)其中,符合要求的条件是
.(直接写出编号)
(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.
20.求证:全等三角形的对应角平分线相等.
21.如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,
求△AEC各内角的度数.
22.如图,请沿图中的虚线,用三种方法将下列图形划分为两个全等图形.
23.已知:△ABC≌△EDC.连接BE,交AC于F,点H是CE上的点,且CH=CF,连接DH交BE于K.求证:∠DKF=∠ACB.
24.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
参考答案
1.解:能够完全重合的两个图形叫做全等形,所以如果两个图形全等,那么这两个图形必定是形状大小均相同.
故选:A.
2.解:∵△ABC与△DEF全等,A和E,B和D分别是对应点
∴BC=DF
∠B=∠D
∠C=∠F
AC=EF.
B、C、D是正确的,A是错误的.
故选:A.
3.解:由题意知真正合同三角形和镜面合同三角形的特点,可判断要使C组的两个三角形重合必须将其中的一个翻转180°;
而其它组的全等三角形可以在平面内通过平移或旋转使它们重合.
故选:C.
4.解:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF,
∴BE=CF,
故A,B,C正确,
故选:D.
5.解:∵△ABC≌△ADE,∠AED=80°,
∴∠C=∠AED=80°,AE=AC,
∴∠AEC=∠C=80°,
∴∠CAE=180°﹣∠C﹣∠AEC=180°﹣80°﹣80°=20°,
故选:D.
6.解:①能够重合的两个图形一定是全等图形,说法正确;
②两个全等图形的面积一定相等,说法正确;
③全等的两个图形的面积相等,但两个面积相等的图形不一定是全等图形,说法错误;
④全等的两个图形的周长相等,两个周长相等的图形不一定是全等图形,说法错误;
故选:A.
7.解:由全等三角形的概念可知:全等的图形是完全重合的,所以①全等图形的形状相同、大小相等是正确的;重合则对应边、对应角是相等的,周长与面积也分别相等,所以①②③④都正确的.
故选:D.
8.解:由于三角形的边长均为整数,且最大边的边长为4,
则三边的长为1,2,3,4四个数中某个或某几个,而1+2=3,1+3=4,
所以三条边不等的组合只能为2,3,4;
当是等腰三角形时只能为3,3,4;3,4,4;2,4,4;1,4,4组成;
当是等边三角形时边可以为4,4,4.
∴符合条件的不全等的三角形最多有6个.
故选:C.
9.解:∵△ABC≌△DEC,
∴∠B=∠DEC=75°,CE=CB,
∴∠CEB=∠B=75°,∠B=∠CEB,
∴∠BCE=180°﹣2×75°=30°,
故选:B.
10.解:如图,∠2、∠3为两个全等三角形的对应角,
所以,∠2=∠3,
△ABC是等腰直角三角形,
所以,∠1+∠3=45°,
所以,∠1+∠2=45°.
故答案为:45.
11.解:∵在△ABC和△AEF中,,
∴△ABC≌△AEF(SAS),
∴∠4=∠2,
∵∠1+∠4=90°,
∴∠1+∠2=90°,
∵AE=DE,∠AED=90°,
∴∠3=45°,
∴∠1+∠2+∠3=135°,
故答案为:135°
12.解:由图可知,图上由实线围成的图形与(1)是全等形的有(2),(3),(6),
故答案为:(2),(3),(6),
13.解:∵△ABC≌△DEF,
∴AB=DE=5,
故答案为:5
14.解:∵△ABC的三边长分别为3cm,4cm,5cm,△ABC≌△DEF,
∴△DEF的三边长分别为3cm,4cm,5cm,
∴△DEF的周长为3+4+5=12(cm),
故答案为:12.
15.解:
在△ACM和△BAN中,,
∴△ACM≌△BAN,
∴∠2=∠CAM,即可得∠1+∠2=90°.
故答案为:90.
16.解:(1)由题意,小长方形的长为(3+2k
)cm,宽为3cm,
∴裁去的每个小长方形面积为(6k+9)(cm2),
故答案为:(6k+9).
(2)由题意,12k+18k=n 6k2(n为正整数),
可得nk=5,
∴n=1,k=5或n=5,k=1,
∴k=1或5,
故答案为:1或5.
17.解:∵△ABC≌△ADE,
∴AE=AC,
∴∠AEC=∠ACE,
∵∠BAC=28°,
∴∠AEC=∠ACE=(180°﹣∠BAC)=76°,
∵△ABC≌△ADE,∠BAC=28°,
∴∠B=∠D,∠DAE=∠BAC=28°,
∴∠B=∠D=∠AEC﹣∠DAE=76°﹣28°=48°,
故答案为:48°.
18.解:∵△ADE≌△BDE,
∴BE=AE.
∴C△AEC=AE+EC+AC=BE+EC+AC=BC+AC.
∵AC:AB:BC=2:3:4,
∴设AC=2x,AB=3x,BC=4x.
∵△ABC的周长比△AEC的周长大6,
∴C△ABC﹣C△AEC=6.
∴(AB+BC+AC)﹣(BC+AC)=6.
∴AB=3x=6.
∴x=2.
∴AC=2x=4,BC=4x=8.
∴C△AEC=BC+AC=8+4=12.
故答案为:12.
19.解:(1)符合要求的条件是①②④,
故答案为:①②④;
(2)选④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,
∵∠BCD=∠B′C′D′,
∴∠BCD﹣∠ACB=∠B′C′D′﹣∠A′C′B′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D,∠DAC=∠D′A′C′,DA=D′A′,
∴∠BAC+∠DAC=∠B′A′C′+∠D′A′C′,
即∠BAD=∠B′A′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
20.已知:如图,△ABC≌△A′B′C′,AD、A′D′是∠BAC和∠B′A′C′的平分线,
求证:AD=A′D′,
证明:∵△ABC≌△A′B′C′,
∴∠B=∠B′,AB=A′B′,
∠BAC=∠B′A′C′,
∵AD平分∠BAC,A′D′平分∠B′A′C′,
∴∠BAD=∠B′A′D′,
∴△ABD≌△A′B′D′,
∴AD=A′D′.
21.解:∵△ABC≌△AEC,
∴∠B=∠E,∠BAC=∠EAC,∠ACB=∠ACE.
∵∠B=30°,∠ACB=85°,
∴∠E=30°,∠ACE=85°,∠ACB=180°﹣∠B﹣∠ACB=65°,
∴∠EAC=65°.
故∠E=30°,∠ACE=85°,∠EAC=65°.
22.解:如图所示:
.
23.证明:∵△ABC≌△EDC,
∴BC=CD,∠ACB=∠DCE,
在△BCF和△DCH中,
∴△BCF≌△DCH(SAS),
∴∠FBC=∠HDC,
在△FBC和△FDK中,
∵∠FBC=∠HDC,∠BFC=∠DFK,
∴∠DKF=∠ACB.
24.解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
一.选择题
1.如果两个图形全等,那么这两个图形必定是( )
A.形状大小均相同
B.形状相同,但大小不同
C.大小相同,但形状不同
D.形状大小均不相同
2.若△ABC与△DEF全等,A和E,B和D分别是对应点,则下列结论错误的是( )
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF
3.全等三角形又叫做合同三角形.平面内的合同三角形分为真正合同三角形和镜面合同三角形.假如△ABC和△A′B′C′是全等三角形,且点A与点A′对应,点B与点B′对应,点C与点C′对应.当沿周界A﹣B﹣C﹣A及A′﹣B′﹣C′﹣A′环绕时,若运动方向相同,则称它们是真正合同三角形(如图①);若运动方向相反,则称它们是镜面合同三角形(如图②).
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个翻转180度.下列各组合同三角形中,属于镜面合同三角形的是( )
A.B.C.D.
4.△ABC≌△DEF,下列结论中不正确的是( )
A.AB=DE
B.BE=CF
C.BC=EF
D.AC=DE
5.如图,△ABC≌△ADE,点E在BC边上,∠AED=80°,则∠CAE的度数为( )
A.80°
B.60°
C.40°
D.20°
6.下列说法:①能够重合的两个图形一定是全等图形;②两个全等图形的面积一定相等;③两个面积相等的图形一定是全等图形;④两个周长相等的图形一定是全等图形.这些说法中正确的是( )
A.①②
B.②③④
C.①②④
D.①②③④
7.下列说法:①全等图形的形状相同、大小相等;②三边对应相等的两个三角形全等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )
A.①②④
B.①③④
C.②③④
D.①②③④
8.已知△ABC的边长均为整数,且最大边的边长为4,那么符合条件的不全等的三角形最多有( )
A.4个
B.5个
C.6个
D.7个
9.如图,△ABC≌△DEC,点E在边AB上,∠DEC=75°,则∠BCE的度数是( )
A.25°
B.30°
C.40°
D.75°
二.填空题
10.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=
°.
11.在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为
.
如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有
.
13.已知△ABC≌△DEF,若AB=5,则DE=
.
14.已知△ABC≌△DEF,且△ABC的三边长分别为3cm,4cm,5cm,则△DEF的周长为
cm.
15.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2=
度.
16.如图,把一张长方形纸板裁去两个边长为3cm的小正方形和两个全等的小长方形,再把剩余部分(阴影部分)四周折起,恰好做成一个有底有盖的长方体纸盒,纸盒底面长方形的长为3kcm,宽为2kcm,则:
(1)裁去的每个小长方形面积为
cm2.(用k的代数式表示)
(2)若长方体纸盒的表面积是底面积的正整数倍,则正整数k的值为
.
17.如图AB,CD相交于点E,若△ABC≌△ADE,∠BAC=28°,则∠B的度数是
.
18.如图,△ABC中,点D、点E分别在边AB、BC上,连结AE、DE,若△ADE≌△BDE,AC:AB:BC=2:3:4,且△ABC的周长比△AEC的周长大6.则△AEC的周长为
.
三.解答题
19.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.
如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.
下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′
(1)其中,符合要求的条件是
.(直接写出编号)
(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.
20.求证:全等三角形的对应角平分线相等.
21.如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,
求△AEC各内角的度数.
22.如图,请沿图中的虚线,用三种方法将下列图形划分为两个全等图形.
23.已知:△ABC≌△EDC.连接BE,交AC于F,点H是CE上的点,且CH=CF,连接DH交BE于K.求证:∠DKF=∠ACB.
24.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
参考答案
1.解:能够完全重合的两个图形叫做全等形,所以如果两个图形全等,那么这两个图形必定是形状大小均相同.
故选:A.
2.解:∵△ABC与△DEF全等,A和E,B和D分别是对应点
∴BC=DF
∠B=∠D
∠C=∠F
AC=EF.
B、C、D是正确的,A是错误的.
故选:A.
3.解:由题意知真正合同三角形和镜面合同三角形的特点,可判断要使C组的两个三角形重合必须将其中的一个翻转180°;
而其它组的全等三角形可以在平面内通过平移或旋转使它们重合.
故选:C.
4.解:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF,
∴BE=CF,
故A,B,C正确,
故选:D.
5.解:∵△ABC≌△ADE,∠AED=80°,
∴∠C=∠AED=80°,AE=AC,
∴∠AEC=∠C=80°,
∴∠CAE=180°﹣∠C﹣∠AEC=180°﹣80°﹣80°=20°,
故选:D.
6.解:①能够重合的两个图形一定是全等图形,说法正确;
②两个全等图形的面积一定相等,说法正确;
③全等的两个图形的面积相等,但两个面积相等的图形不一定是全等图形,说法错误;
④全等的两个图形的周长相等,两个周长相等的图形不一定是全等图形,说法错误;
故选:A.
7.解:由全等三角形的概念可知:全等的图形是完全重合的,所以①全等图形的形状相同、大小相等是正确的;重合则对应边、对应角是相等的,周长与面积也分别相等,所以①②③④都正确的.
故选:D.
8.解:由于三角形的边长均为整数,且最大边的边长为4,
则三边的长为1,2,3,4四个数中某个或某几个,而1+2=3,1+3=4,
所以三条边不等的组合只能为2,3,4;
当是等腰三角形时只能为3,3,4;3,4,4;2,4,4;1,4,4组成;
当是等边三角形时边可以为4,4,4.
∴符合条件的不全等的三角形最多有6个.
故选:C.
9.解:∵△ABC≌△DEC,
∴∠B=∠DEC=75°,CE=CB,
∴∠CEB=∠B=75°,∠B=∠CEB,
∴∠BCE=180°﹣2×75°=30°,
故选:B.
10.解:如图,∠2、∠3为两个全等三角形的对应角,
所以,∠2=∠3,
△ABC是等腰直角三角形,
所以,∠1+∠3=45°,
所以,∠1+∠2=45°.
故答案为:45.
11.解:∵在△ABC和△AEF中,,
∴△ABC≌△AEF(SAS),
∴∠4=∠2,
∵∠1+∠4=90°,
∴∠1+∠2=90°,
∵AE=DE,∠AED=90°,
∴∠3=45°,
∴∠1+∠2+∠3=135°,
故答案为:135°
12.解:由图可知,图上由实线围成的图形与(1)是全等形的有(2),(3),(6),
故答案为:(2),(3),(6),
13.解:∵△ABC≌△DEF,
∴AB=DE=5,
故答案为:5
14.解:∵△ABC的三边长分别为3cm,4cm,5cm,△ABC≌△DEF,
∴△DEF的三边长分别为3cm,4cm,5cm,
∴△DEF的周长为3+4+5=12(cm),
故答案为:12.
15.解:
在△ACM和△BAN中,,
∴△ACM≌△BAN,
∴∠2=∠CAM,即可得∠1+∠2=90°.
故答案为:90.
16.解:(1)由题意,小长方形的长为(3+2k
)cm,宽为3cm,
∴裁去的每个小长方形面积为(6k+9)(cm2),
故答案为:(6k+9).
(2)由题意,12k+18k=n 6k2(n为正整数),
可得nk=5,
∴n=1,k=5或n=5,k=1,
∴k=1或5,
故答案为:1或5.
17.解:∵△ABC≌△ADE,
∴AE=AC,
∴∠AEC=∠ACE,
∵∠BAC=28°,
∴∠AEC=∠ACE=(180°﹣∠BAC)=76°,
∵△ABC≌△ADE,∠BAC=28°,
∴∠B=∠D,∠DAE=∠BAC=28°,
∴∠B=∠D=∠AEC﹣∠DAE=76°﹣28°=48°,
故答案为:48°.
18.解:∵△ADE≌△BDE,
∴BE=AE.
∴C△AEC=AE+EC+AC=BE+EC+AC=BC+AC.
∵AC:AB:BC=2:3:4,
∴设AC=2x,AB=3x,BC=4x.
∵△ABC的周长比△AEC的周长大6,
∴C△ABC﹣C△AEC=6.
∴(AB+BC+AC)﹣(BC+AC)=6.
∴AB=3x=6.
∴x=2.
∴AC=2x=4,BC=4x=8.
∴C△AEC=BC+AC=8+4=12.
故答案为:12.
19.解:(1)符合要求的条件是①②④,
故答案为:①②④;
(2)选④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,
∵∠BCD=∠B′C′D′,
∴∠BCD﹣∠ACB=∠B′C′D′﹣∠A′C′B′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D,∠DAC=∠D′A′C′,DA=D′A′,
∴∠BAC+∠DAC=∠B′A′C′+∠D′A′C′,
即∠BAD=∠B′A′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
20.已知:如图,△ABC≌△A′B′C′,AD、A′D′是∠BAC和∠B′A′C′的平分线,
求证:AD=A′D′,
证明:∵△ABC≌△A′B′C′,
∴∠B=∠B′,AB=A′B′,
∠BAC=∠B′A′C′,
∵AD平分∠BAC,A′D′平分∠B′A′C′,
∴∠BAD=∠B′A′D′,
∴△ABD≌△A′B′D′,
∴AD=A′D′.
21.解:∵△ABC≌△AEC,
∴∠B=∠E,∠BAC=∠EAC,∠ACB=∠ACE.
∵∠B=30°,∠ACB=85°,
∴∠E=30°,∠ACE=85°,∠ACB=180°﹣∠B﹣∠ACB=65°,
∴∠EAC=65°.
故∠E=30°,∠ACE=85°,∠EAC=65°.
22.解:如图所示:
.
23.证明:∵△ABC≌△EDC,
∴BC=CD,∠ACB=∠DCE,
在△BCF和△DCH中,
∴△BCF≌△DCH(SAS),
∴∠FBC=∠HDC,
在△FBC和△FDK中,
∵∠FBC=∠HDC,∠BFC=∠DFK,
∴∠DKF=∠ACB.
24.解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
