人教版2021年八年级数学上册12.2《全等三角形的判定》同步练习卷 (Word版含解析)
文档属性
| 名称 | 人教版2021年八年级数学上册12.2《全等三角形的判定》同步练习卷 (Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 201.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 10:04:36 | ||
图片预览



文档简介
人教版2021年八年级数学上册12.2《全等三角形的判定》同步练习卷
一.选择题
1.某同学把一块三角形的玻璃打碎也成了三块,现在要到玻璃店去配一块完全一样的玻璃,他选择带(3)号玻璃去,配回来的玻璃与原来的恰好一样,请问他选择三号的理论依据是( )
A.SSS
B.SAS
C.AAS
D.ASA
2.下列各条件中能判断两个直角三角形全等的是( )
A.一对锐角相等
B.两对锐角相等
C.一组边对应相等
D.一组锐角和斜边分别相等
3.下列条件中一定能判定△ABC≌△DEF的是( )
A.∠A=∠D,∠B=∠E,∠C=∠F
B.∠A=∠D,AB=DE,BC=EF
C.AB=DE,AC=DF,BC=EF
D.AB=DE,∠A=∠E,∠B=∠F
4.如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件,这个条件不能是( )
A.∠A=∠D
B.∠ACB=∠DBC
C.AC=BD
D.AB=DC
5.如图,点A在DE上,AC=EC,∠1=∠2=∠3,则DE等于( )
A.AB
B.BC
C.DC
D.AE+AC
6.如图,点E,F在线段BC上,△ABF与△DEC全等,点A和点D,点B和点C是对应点,AF和DE交于点M,则与EM相等的线段是( )
A.BE
B.EF
C.FC
D.MF
7.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有多少对( )
A.3对
B.4对
C.5对
D.6对
8.如图,在5×5的正方形网格中,△ABC的三个顶点都在格点上,则与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点都在格点上的三角形)共有( )
A.5个
B.6个
C.7个
D.8个
二.填空题
9.如图,小明站在堤岸的A点处,正对他的s点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C、D间的距离为90米,则在A点处小明与游艇的距离为
米.
10.如图,已知BE⊥CD,BE=DE,BC=DA,CD=6,且CE:DE=1:2,则AB的长为
.
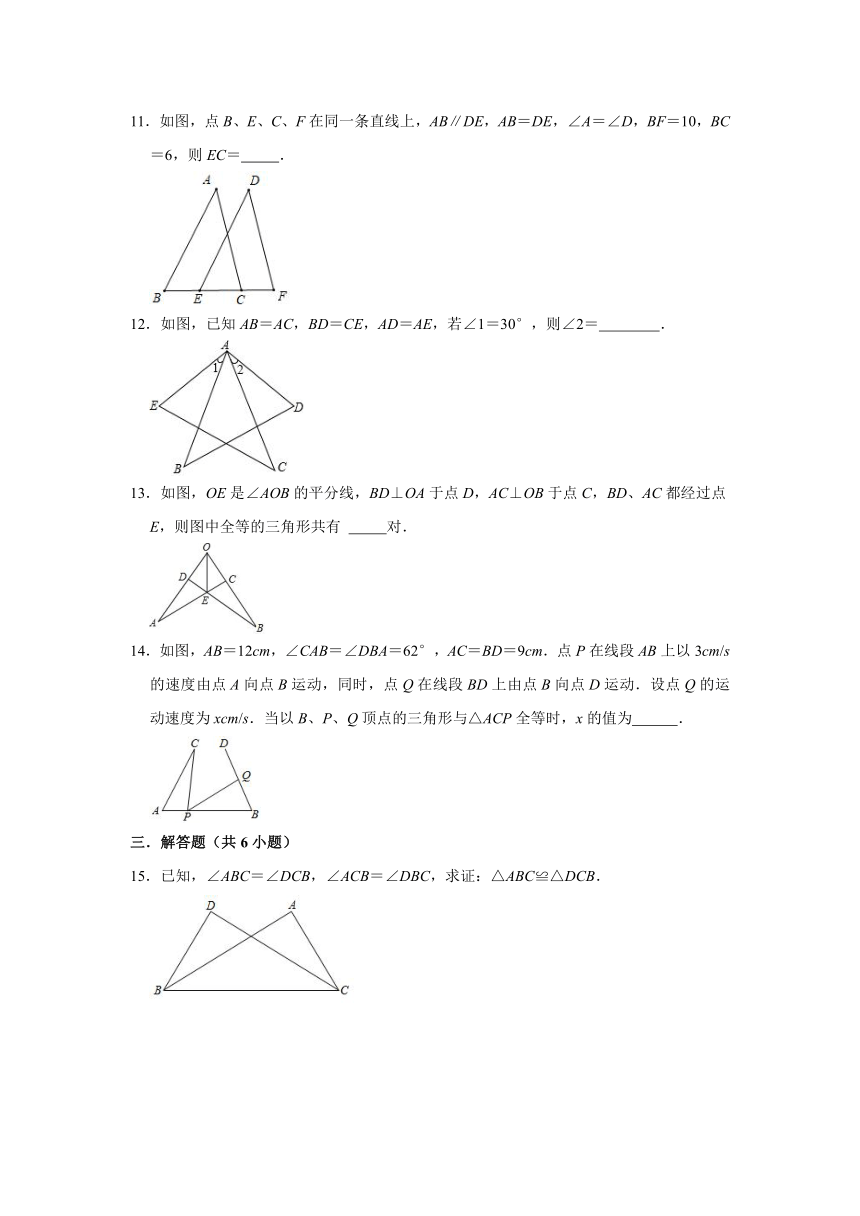
11.如图,点B、E、C、F在同一条直线上,AB∥DE,AB=DE,∠A=∠D,BF=10,BC=6,则EC=
.
12.如图,已知AB=AC,BD=CE,AD=AE,若∠1=30°,则∠2=
.
13.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有
对.
14.如图,AB=12cm,∠CAB=∠DBA=62°,AC=BD=9cm.点P在线段AB上以3cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设点Q的运动速度为xcm/s.当以B、P、Q顶点的三角形与△ACP全等时,x的值为
.
三.解答题(共6小题)
15.已知,∠ABC=∠DCB,∠ACB=∠DBC,求证:△ABC≌△DCB.
16.如图,B、C、D、E在同一条直线上,AB∥EF,BC=DE,AB=EF,求证:AC=DF.
17.已知:如图,∠A=∠D=90°,AC=BD.求证:AB=CD.
18.已知如图,AB=AC,点D为BC上一点,∠DAE=∠BAC,AD=AE,连接EC,求证:BD=CE.
19.如图,分别过点C、B作△ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E、F.
(1)求证:BF=CE;
(2)若△ACE的面积为4,△CED的面积为3,求△ABF的面积.
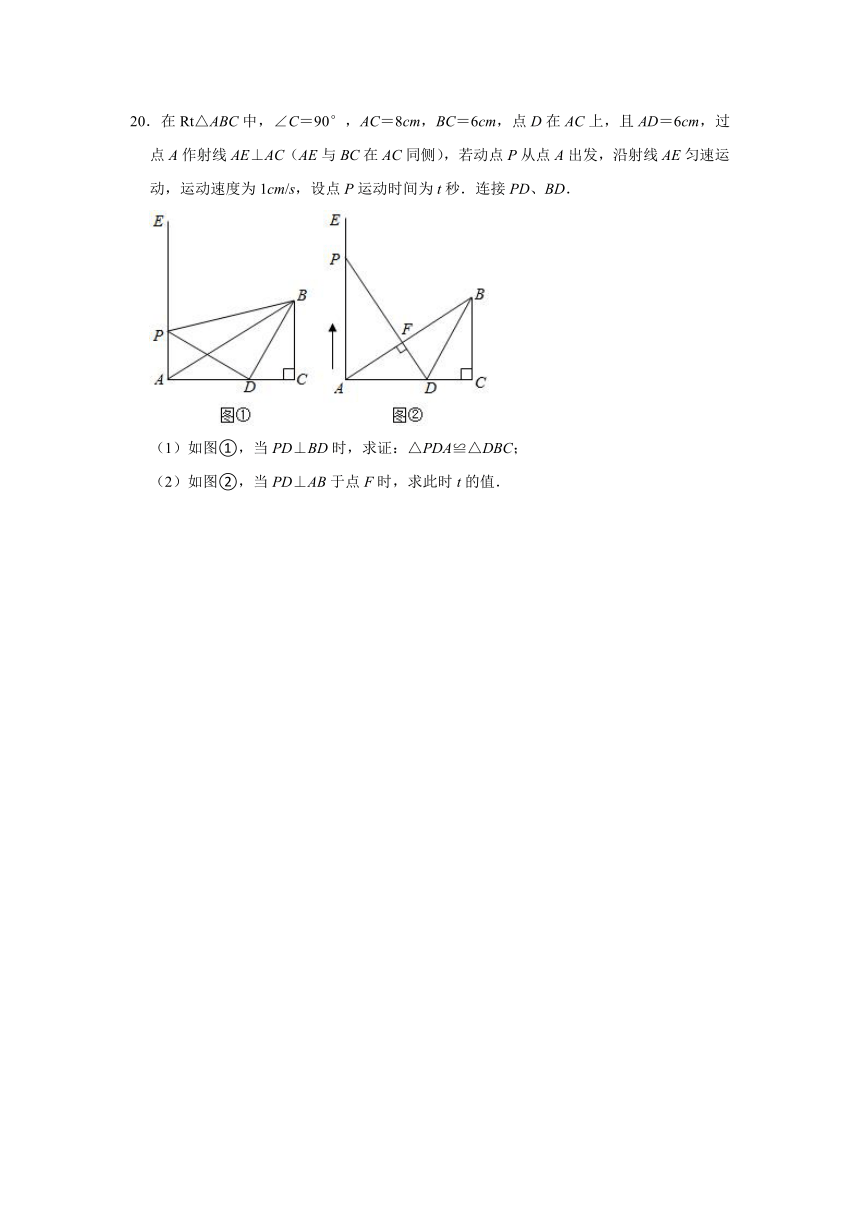
20.在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AC上,且AD=6cm,过点A作射线AE⊥AC(AE与BC在AC同侧),若动点P从点A出发,沿射线AE匀速运动,运动速度为1cm/s,设点P运动时间为t秒.连接PD、BD.
(1)如图①,当PD⊥BD时,求证:△PDA≌△DBC;
(2)如图②,当PD⊥AB于点F时,求此时t的值.
参考答案
一.选择题
1.解:∵第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.
∴选择三号的理论依据是ASA,
故选:D.
2.解:A、一对锐角相等,不能判定两直角三角形全等,故此选项不符合题意;
B、两对锐角相等,不能判定两直角三角形全等,故此选项不符合题意;
C、一组边对应相等,不能判定两直角三角形全等,故此选项不符合题意;
D、一组锐角和斜边分别相等,能判定两直角三角形全等,故此选项符合题意;
故选:D.
3.解:
A、根据∠A=∠D,∠B=∠E,∠C=∠F不能推出△ABC≌△DEF,故本选项不符合题意;
B、根据∠A=∠D,AB=DE,BC=EF不能推出△ABC≌△DEF,故本选项不符合题意;
C、符合全等三角形的判定定理SSS,能推出△ABC≌△DEF,故本选项符合题意;
D、根据AB=DE,∠A=∠E,∠B=∠F不能推出△ABC≌△DEF,故本选项不符合题意;
故选:C.
4.解:A、在△ABC和△DCB中,
,
∴△ABC≌△DCB(AAS),故本选项不符合题意;
B、在△ABC和△DCB中,
,
∴△ABC≌△DCB(ASA),故本选项不符合题意;
C、根据两边和其中一边的对角不能判断两三角形全等,故本选项符合题意;
D、在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS),故本选项不符合题意;
故选:C.
5.解:∵∠1=∠2,
∴∠B=∠D,
∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,
即∠ACB=∠ECD,
在△ACB和△ECD中,
,
∴△ACB≌△ECD(AAS),
∴AB=ED.
故选:A.
6.解:∵△ABF与△DEC全等,
∴∠DEC=∠AFB,
∴ME=MF,
故选:D.
7.解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS).
故选:B.
8.解:如图所示,
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出△ABG,△ABM,△ABH三个三角形和原三角形全等.
以AC为公共边不可以画出一个三角形和原三角形全等,
所以可画出6个.
故选:B.
二.填空题
9.解:在△ABS与△CBD中,
,
∴△ABS≌△CBD(ASA),
∴AS=CD,
∵CD=90米,
∴AS=CD=90米,
答:在A点处小明与游艇的距离为90米,
故答案为:90米.
10.解:∵CD=6,且CE:DE=1:2,
∴CE=2,DE=4.
在Rt△BCE和Rt△DAE中,
.
∴Rt△△BCE≌Rt△DAE(HL).
∴AE=CE=2,BE=DE=4.
∴AB=BE﹣AE=2.
故答案是:2.
11.解:∵AB∥DE,
∴∠B=∠DEF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴BC=EF,
∵BF=10,BC=6,
∴EF=6,CF=BF﹣BC=4,
∴EC=EF﹣CF=2,
故答案为:2.
12.解:在△ABD和△ACE中,
,
∴△ABD≌△ACE(SSS),
∴∠BAD=∠EAC,
∴∠1=∠2,
∵∠1=30°,
∴∠2=30°.
故答案为30°.
13.解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS).
故答案为4.
14.解:①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
,
解得;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得;
综上所述,当x=3或时,△ACP与△BPQ全等.
故答案为3或.
三.解答题(共6小题)
15.证明:在△ABC与△DCB中,
,
∴△ABC≌△DCB(ASA).
16.证明:∵AB∥EF,
∴∠B=∠E,
在△ACB和△FDE中,
,
∴△ACB≌△FDE(SAS),
∴AC=DF.
17.证明:连接BC,
∵∠A=∠D=90°,
∴△ABC和△DCB都是直角三角形.
在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL).
∴AB=CD.
18.证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE.
19.解:(1)∵CE⊥AD,BF⊥AF,
∴∠CED=∠BFD=90°,
∵AD是△ABC的中线,
∴BD=CD,
在△CED和△BFD中,
,
∴△CED≌△BFD(AAS),
∴BF=CE;
(2)∵AD是△ABC的中线,
∴S△ABD=S△ACD,
∵S△ACE=4,SCED=3,
∴S△ACD=S△ABD=7,
∵△BFD≌△CED,
∴S△BDF=S△CED=3,
∴S△ABF=S△ABD+S△BDF=7+3=10.
20.(1)证明:如图①,∵PD⊥BD,
∴∠PDB=90°,
∴∠BDC+∠PDA=90°,
又∵∠C=90°,
∴∠BDC+∠CBD=90°,
∴∠PDA=∠CBD,
又∵AE⊥AC,
∴∠PAD=90°,
∴∠PAD=∠C=90°,
又∵BC=6cm,AD=6cm,
∴AD=BC,
在△PAD和△DCB中,
,
∴△PDA≌△DBC(ASA);
(2)解:如图②,∵PD⊥AB,
∴∠AFD=∠AFP=90°,
∴∠PAF+∠APF=90°,
又∵AE⊥AC,
∴∠PAF+∠CAB=90°,
∴∠APF=∠CAB,
在△APD和△CAB中,
,
∴△APD≌△CAB(AAS),
∴AP=AC,
∵AC=8cm,
∴AP=8cm,
∴t=8.
一.选择题
1.某同学把一块三角形的玻璃打碎也成了三块,现在要到玻璃店去配一块完全一样的玻璃,他选择带(3)号玻璃去,配回来的玻璃与原来的恰好一样,请问他选择三号的理论依据是( )
A.SSS
B.SAS
C.AAS
D.ASA
2.下列各条件中能判断两个直角三角形全等的是( )
A.一对锐角相等
B.两对锐角相等
C.一组边对应相等
D.一组锐角和斜边分别相等
3.下列条件中一定能判定△ABC≌△DEF的是( )
A.∠A=∠D,∠B=∠E,∠C=∠F
B.∠A=∠D,AB=DE,BC=EF
C.AB=DE,AC=DF,BC=EF
D.AB=DE,∠A=∠E,∠B=∠F
4.如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件,这个条件不能是( )
A.∠A=∠D
B.∠ACB=∠DBC
C.AC=BD
D.AB=DC
5.如图,点A在DE上,AC=EC,∠1=∠2=∠3,则DE等于( )
A.AB
B.BC
C.DC
D.AE+AC
6.如图,点E,F在线段BC上,△ABF与△DEC全等,点A和点D,点B和点C是对应点,AF和DE交于点M,则与EM相等的线段是( )
A.BE
B.EF
C.FC
D.MF
7.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有多少对( )
A.3对
B.4对
C.5对
D.6对
8.如图,在5×5的正方形网格中,△ABC的三个顶点都在格点上,则与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点都在格点上的三角形)共有( )
A.5个
B.6个
C.7个
D.8个
二.填空题
9.如图,小明站在堤岸的A点处,正对他的s点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C、D间的距离为90米,则在A点处小明与游艇的距离为
米.
10.如图,已知BE⊥CD,BE=DE,BC=DA,CD=6,且CE:DE=1:2,则AB的长为
.
11.如图,点B、E、C、F在同一条直线上,AB∥DE,AB=DE,∠A=∠D,BF=10,BC=6,则EC=
.
12.如图,已知AB=AC,BD=CE,AD=AE,若∠1=30°,则∠2=
.
13.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥OB于点C,BD、AC都经过点E,则图中全等的三角形共有
对.
14.如图,AB=12cm,∠CAB=∠DBA=62°,AC=BD=9cm.点P在线段AB上以3cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设点Q的运动速度为xcm/s.当以B、P、Q顶点的三角形与△ACP全等时,x的值为
.
三.解答题(共6小题)
15.已知,∠ABC=∠DCB,∠ACB=∠DBC,求证:△ABC≌△DCB.
16.如图,B、C、D、E在同一条直线上,AB∥EF,BC=DE,AB=EF,求证:AC=DF.
17.已知:如图,∠A=∠D=90°,AC=BD.求证:AB=CD.
18.已知如图,AB=AC,点D为BC上一点,∠DAE=∠BAC,AD=AE,连接EC,求证:BD=CE.
19.如图,分别过点C、B作△ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E、F.
(1)求证:BF=CE;
(2)若△ACE的面积为4,△CED的面积为3,求△ABF的面积.
20.在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AC上,且AD=6cm,过点A作射线AE⊥AC(AE与BC在AC同侧),若动点P从点A出发,沿射线AE匀速运动,运动速度为1cm/s,设点P运动时间为t秒.连接PD、BD.
(1)如图①,当PD⊥BD时,求证:△PDA≌△DBC;
(2)如图②,当PD⊥AB于点F时,求此时t的值.
参考答案
一.选择题
1.解:∵第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.
∴选择三号的理论依据是ASA,
故选:D.
2.解:A、一对锐角相等,不能判定两直角三角形全等,故此选项不符合题意;
B、两对锐角相等,不能判定两直角三角形全等,故此选项不符合题意;
C、一组边对应相等,不能判定两直角三角形全等,故此选项不符合题意;
D、一组锐角和斜边分别相等,能判定两直角三角形全等,故此选项符合题意;
故选:D.
3.解:
A、根据∠A=∠D,∠B=∠E,∠C=∠F不能推出△ABC≌△DEF,故本选项不符合题意;
B、根据∠A=∠D,AB=DE,BC=EF不能推出△ABC≌△DEF,故本选项不符合题意;
C、符合全等三角形的判定定理SSS,能推出△ABC≌△DEF,故本选项符合题意;
D、根据AB=DE,∠A=∠E,∠B=∠F不能推出△ABC≌△DEF,故本选项不符合题意;
故选:C.
4.解:A、在△ABC和△DCB中,
,
∴△ABC≌△DCB(AAS),故本选项不符合题意;
B、在△ABC和△DCB中,
,
∴△ABC≌△DCB(ASA),故本选项不符合题意;
C、根据两边和其中一边的对角不能判断两三角形全等,故本选项符合题意;
D、在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS),故本选项不符合题意;
故选:C.
5.解:∵∠1=∠2,
∴∠B=∠D,
∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,
即∠ACB=∠ECD,
在△ACB和△ECD中,
,
∴△ACB≌△ECD(AAS),
∴AB=ED.
故选:A.
6.解:∵△ABF与△DEC全等,
∴∠DEC=∠AFB,
∴ME=MF,
故选:D.
7.解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS).
故选:B.
8.解:如图所示,
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出△ABG,△ABM,△ABH三个三角形和原三角形全等.
以AC为公共边不可以画出一个三角形和原三角形全等,
所以可画出6个.
故选:B.
二.填空题
9.解:在△ABS与△CBD中,
,
∴△ABS≌△CBD(ASA),
∴AS=CD,
∵CD=90米,
∴AS=CD=90米,
答:在A点处小明与游艇的距离为90米,
故答案为:90米.
10.解:∵CD=6,且CE:DE=1:2,
∴CE=2,DE=4.
在Rt△BCE和Rt△DAE中,
.
∴Rt△△BCE≌Rt△DAE(HL).
∴AE=CE=2,BE=DE=4.
∴AB=BE﹣AE=2.
故答案是:2.
11.解:∵AB∥DE,
∴∠B=∠DEF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴BC=EF,
∵BF=10,BC=6,
∴EF=6,CF=BF﹣BC=4,
∴EC=EF﹣CF=2,
故答案为:2.
12.解:在△ABD和△ACE中,
,
∴△ABD≌△ACE(SSS),
∴∠BAD=∠EAC,
∴∠1=∠2,
∵∠1=30°,
∴∠2=30°.
故答案为30°.
13.解:∵OE是∠AOB的平分线,BD⊥OA,AC⊥OB,
∴ED=EC,
在Rt△OED和△OEC中,
,
∴Rt△OED≌Rt△OEC(HL);
∴OD=OC,
在△AED和△BEC中,
,
∴△AED≌△BEC(ASA);
∴AD=BC,
∴OD+AD=OC+BC,即OA=OB,
在△OAE和△OBE中,
,
∴△OAE≌△OBE(SAS),
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS).
故答案为4.
14.解:①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
,
解得;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得;
综上所述,当x=3或时,△ACP与△BPQ全等.
故答案为3或.
三.解答题(共6小题)
15.证明:在△ABC与△DCB中,
,
∴△ABC≌△DCB(ASA).
16.证明:∵AB∥EF,
∴∠B=∠E,
在△ACB和△FDE中,
,
∴△ACB≌△FDE(SAS),
∴AC=DF.
17.证明:连接BC,
∵∠A=∠D=90°,
∴△ABC和△DCB都是直角三角形.
在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL).
∴AB=CD.
18.证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE.
19.解:(1)∵CE⊥AD,BF⊥AF,
∴∠CED=∠BFD=90°,
∵AD是△ABC的中线,
∴BD=CD,
在△CED和△BFD中,
,
∴△CED≌△BFD(AAS),
∴BF=CE;
(2)∵AD是△ABC的中线,
∴S△ABD=S△ACD,
∵S△ACE=4,SCED=3,
∴S△ACD=S△ABD=7,
∵△BFD≌△CED,
∴S△BDF=S△CED=3,
∴S△ABF=S△ABD+S△BDF=7+3=10.
20.(1)证明:如图①,∵PD⊥BD,
∴∠PDB=90°,
∴∠BDC+∠PDA=90°,
又∵∠C=90°,
∴∠BDC+∠CBD=90°,
∴∠PDA=∠CBD,
又∵AE⊥AC,
∴∠PAD=90°,
∴∠PAD=∠C=90°,
又∵BC=6cm,AD=6cm,
∴AD=BC,
在△PAD和△DCB中,
,
∴△PDA≌△DBC(ASA);
(2)解:如图②,∵PD⊥AB,
∴∠AFD=∠AFP=90°,
∴∠PAF+∠APF=90°,
又∵AE⊥AC,
∴∠PAF+∠CAB=90°,
∴∠APF=∠CAB,
在△APD和△CAB中,
,
∴△APD≌△CAB(AAS),
∴AP=AC,
∵AC=8cm,
∴AP=8cm,
∴t=8.
