2.3.2一元二次不等式的应用课件(共11张PPT)-2021--2022学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 2.3.2一元二次不等式的应用课件(共11张PPT)-2021--2022学年高一上学期数学人教A版(2019)必修第一册 |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 12:32:12 | ||
图片预览




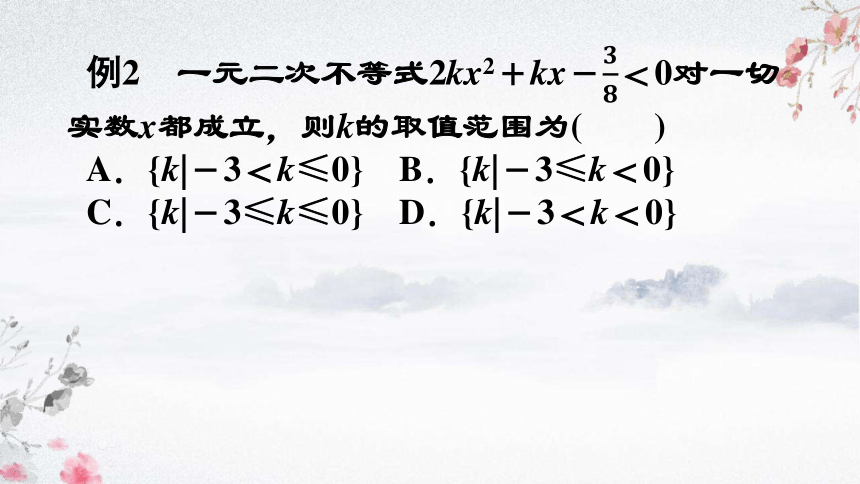
文档简介
(共11张PPT)
一元二次不等式的应用
题型1 简单分式不等式的解法
例1 解下列不等式:
(1)<0;(2)≥0;(3)>1.
新知生成
解分式不等式时,要注意先移项,使右边化为0,要注意含等号的分式不等式的分母不为0.
等价转化为一元二次不等式或者一元一次不等式组求得.
跟踪训练1 (1)不等式≥0的解集为( )
A.{x|-6≤x≤1}
B.{x|x≥1或x≤-6}
C.{x|-6≤x<1}
D.{x|x>1或x≤-6}
(2)不等式≤2的解集为__________.
题型2 不等式恒成立问题
角度1 在R上恒成立问题
思考1:一元二次不等式ax +bx+c≥0的解集为R,则二次函数y=ax +bx+c的图象是怎样的?
思考2:若一元二次不等式ax +bx+c≤0的解集为R,则a、b、c应满足什么关系?
例2 一元二次不等式2kx2+kx-<0对一切实数x都成立,则k的取值范围为( )
A.{k|-3<k≤0}
B.{k|-3≤k<0}
C.{k|-3≤k≤0}
D.{k|-3<k<0}
跟踪训练2 (1)设a为常数, x∈R,ax2+ax+1>0,则a的取值范围是( )
A.{x|0<a<4}
B.{x|0≤a<4}
C.{x|a>0}
D.{x|a<4}
角度2 在给定范围内的恒成立问题
一般地,“不等式ax +bx+c>0在{x|}
上恒成立”的几何意义是
函数y=ax +bx+c在{x|}上的图象全部在x轴上方.
{x|}是不等式ax +bx+c>0的解集的子集.
例3 设函数y=mx2-mx-1.
(1)若对于一切实数x,y<0恒成立,求m的取值范围;
(2)对于x∈{x|1≤x≤3},y<-m+5恒成立,求m的取值范围.
跟踪训练2
(2)若对于任意x∈{x|m≤x≤m+1},都有x2+mx-1<0成立,则实数m的取值范围是______________.
题型3 一元二次不等式的实际应用
例4 某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品x(百台),其总成本为p万元(总成本=固定成本+生产成本),并且销售收入y满足
y=
假定该产品产销平衡,根据上述统计规律求:
(1)要使工厂有盈利,产品数量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?
课堂小结
1.分式不等式转化为一元二次不等式,但要注意分母为不为0.
2.不等式恒成立求参数范围问题
常用方法是分离参数法或者利用不等式与二次函数的关系通过函数关系直观判断
对于y=ax +bx+c恒成立的不等式问题
k≥y恒成立 k≥y的最大值
k≤y恒成立 k≤y的最小值
3.实际应用问题
建立数学模型,找准不等关系,用不等式表示不等关系,解不等式,回答实际问题.
一元二次不等式的应用
题型1 简单分式不等式的解法
例1 解下列不等式:
(1)<0;(2)≥0;(3)>1.
新知生成
解分式不等式时,要注意先移项,使右边化为0,要注意含等号的分式不等式的分母不为0.
等价转化为一元二次不等式或者一元一次不等式组求得.
跟踪训练1 (1)不等式≥0的解集为( )
A.{x|-6≤x≤1}
B.{x|x≥1或x≤-6}
C.{x|-6≤x<1}
D.{x|x>1或x≤-6}
(2)不等式≤2的解集为__________.
题型2 不等式恒成立问题
角度1 在R上恒成立问题
思考1:一元二次不等式ax +bx+c≥0的解集为R,则二次函数y=ax +bx+c的图象是怎样的?
思考2:若一元二次不等式ax +bx+c≤0的解集为R,则a、b、c应满足什么关系?
例2 一元二次不等式2kx2+kx-<0对一切实数x都成立,则k的取值范围为( )
A.{k|-3<k≤0}
B.{k|-3≤k<0}
C.{k|-3≤k≤0}
D.{k|-3<k<0}
跟踪训练2 (1)设a为常数, x∈R,ax2+ax+1>0,则a的取值范围是( )
A.{x|0<a<4}
B.{x|0≤a<4}
C.{x|a>0}
D.{x|a<4}
角度2 在给定范围内的恒成立问题
一般地,“不等式ax +bx+c>0在{x|}
上恒成立”的几何意义是
函数y=ax +bx+c在{x|}上的图象全部在x轴上方.
{x|}是不等式ax +bx+c>0的解集的子集.
例3 设函数y=mx2-mx-1.
(1)若对于一切实数x,y<0恒成立,求m的取值范围;
(2)对于x∈{x|1≤x≤3},y<-m+5恒成立,求m的取值范围.
跟踪训练2
(2)若对于任意x∈{x|m≤x≤m+1},都有x2+mx-1<0成立,则实数m的取值范围是______________.
题型3 一元二次不等式的实际应用
例4 某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品x(百台),其总成本为p万元(总成本=固定成本+生产成本),并且销售收入y满足
y=
假定该产品产销平衡,根据上述统计规律求:
(1)要使工厂有盈利,产品数量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?
课堂小结
1.分式不等式转化为一元二次不等式,但要注意分母为不为0.
2.不等式恒成立求参数范围问题
常用方法是分离参数法或者利用不等式与二次函数的关系通过函数关系直观判断
对于y=ax +bx+c恒成立的不等式问题
k≥y恒成立 k≥y的最大值
k≤y恒成立 k≤y的最小值
3.实际应用问题
建立数学模型,找准不等关系,用不等式表示不等关系,解不等式,回答实际问题.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
