12.2三角形全等的判定 同步能力提升训练 2021-2022学年八年级数学人教版上册(Word版含答案)
文档属性
| 名称 | 12.2三角形全等的判定 同步能力提升训练 2021-2022学年八年级数学人教版上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 15:09:55 | ||
图片预览

文档简介
2021-2022人教版八年级数学上册《12.2三角形全等的判定》同步能力提升训练(附答案)
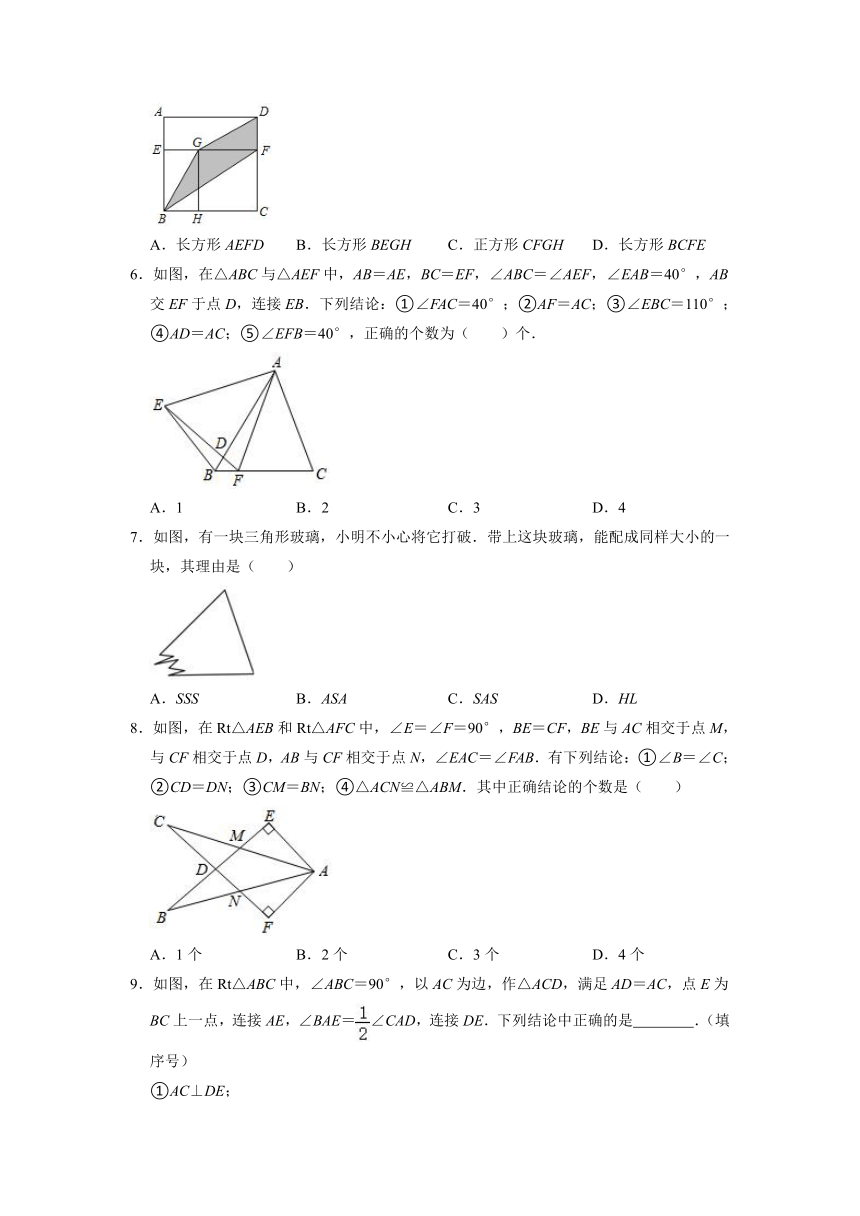
1.如图,BC⊥AC,BD⊥AD,且AB平分∠CAD,则利用( )可说明△ABC与△ABD全等.
A.AAS
B.ASA
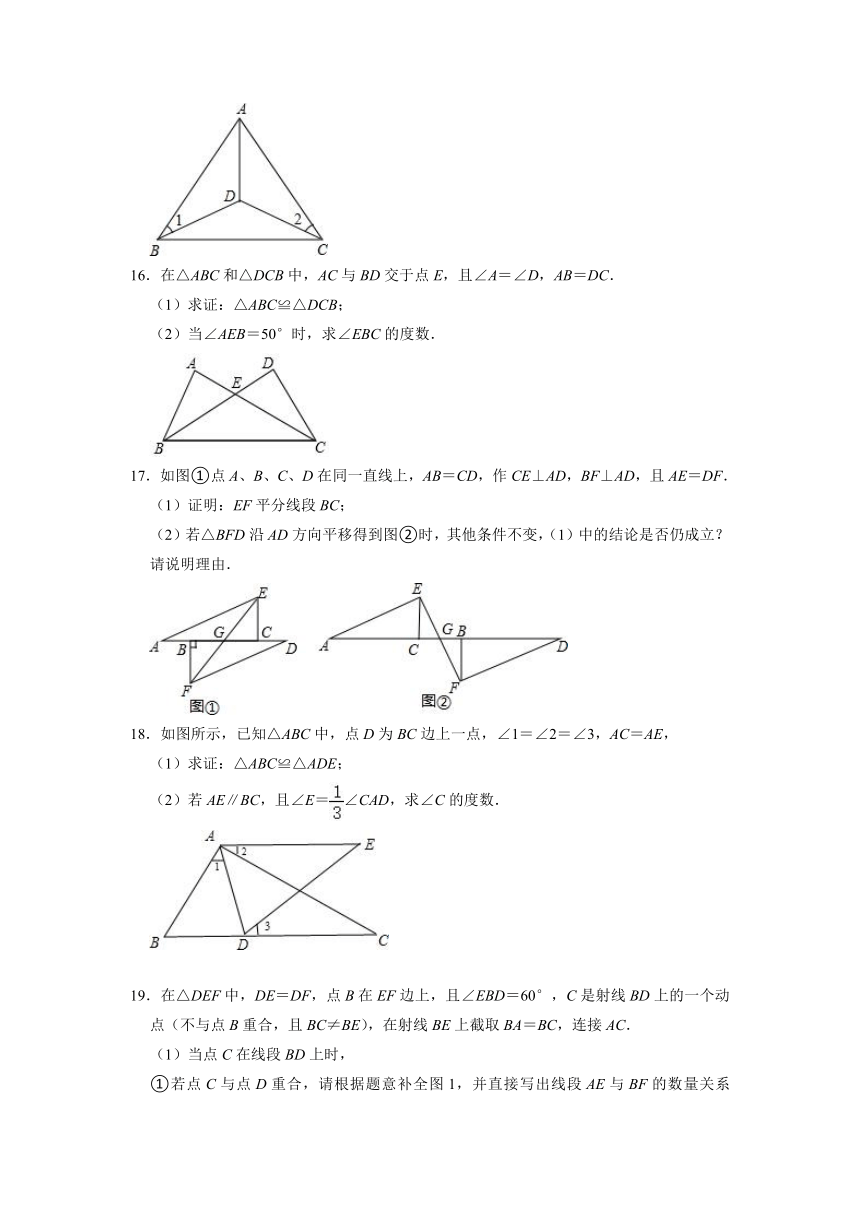
C.SAS
D.SSA
2.如图,BC∥EF,BC=EF,要使得△ABC≌△DEF,需要补充的条件不能是( )
A.∠B=∠E
B.AB=DE
C.AD=CF
D.AB∥DE
3.如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.那么C,D两点间的距离就是在A点处小明与游艇的距离.在这个问题中,可作为证明△SAB≌△DCB的依据的是( )
A.SAS或SSS
B.AAS或SSS
C.ASA或AAS
D.ASA或SAS
4.如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6.5,则BD的长为( )
A.1
B.2
C.2.5
D.3
5.如图,正方形ABCD被分割成2个长方形和1个正方形,要求图中阴影部分的面积,只要知道下列图形的面积是( )
A.长方形AEFD
B.长方形BEGH
C.正方形CFGH
D.长方形BCFE
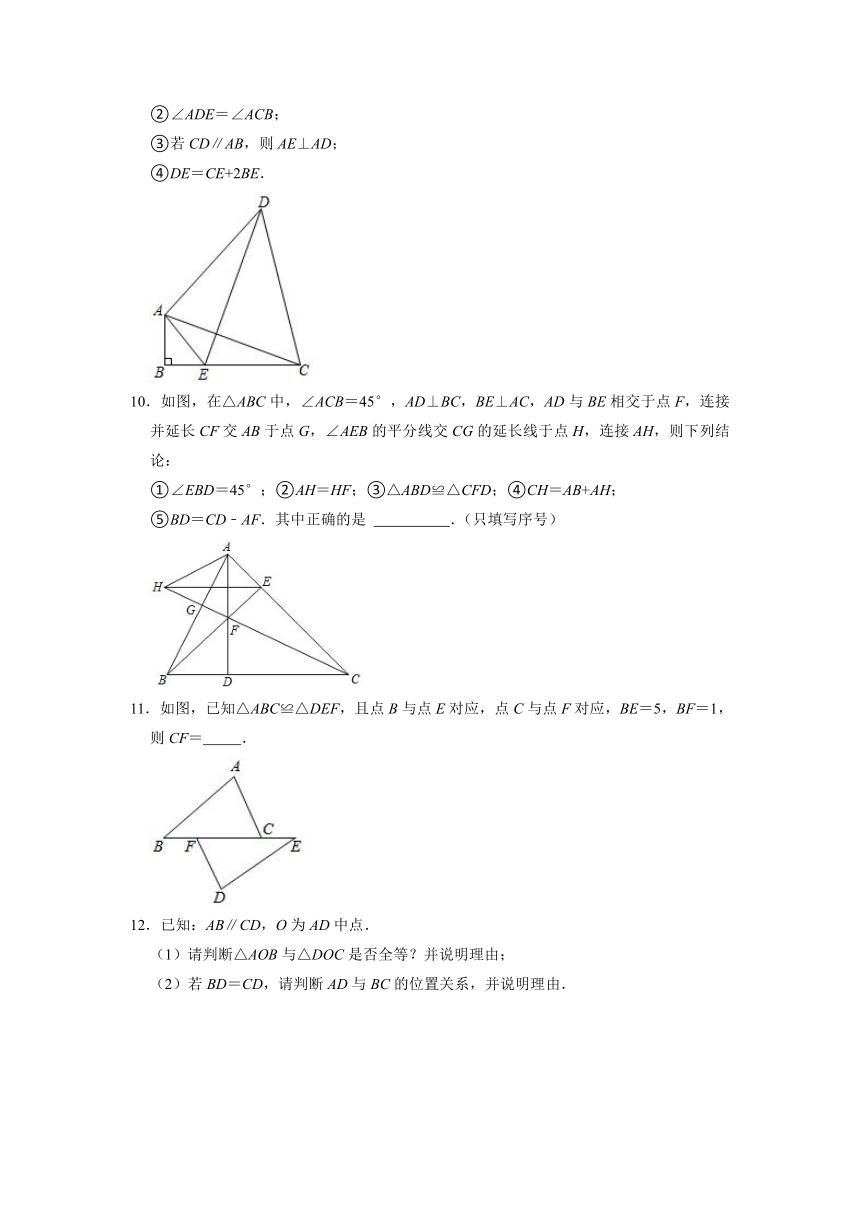
6.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EBC=110°;④AD=AC;⑤∠EFB=40°,正确的个数为( )个.
A.1
B.2
C.3
D.4
7.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A.SSS
B.ASA
C.SAS
D.HL
8.如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
9.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,点E为BC上一点,连接AE,∠BAE=∠CAD,连接DE.下列结论中正确的是
.(填序号)
①AC⊥DE;
②∠ADE=∠ACB;
③若CD∥AB,则AE⊥AD;
④DE=CE+2BE.
10.如图,在△ABC中,∠ACB=45°,AD⊥BC,BE⊥AC,AD与BE相交于点F,连接并延长CF交AB于点G,∠AEB的平分线交CG的延长线于点H,连接AH,则下列结论:
①∠EBD=45°;②AH=HF;③△ABD≌△CFD;④CH=AB+AH;
⑤BD=CD﹣AF.其中正确的是
.(只填写序号)
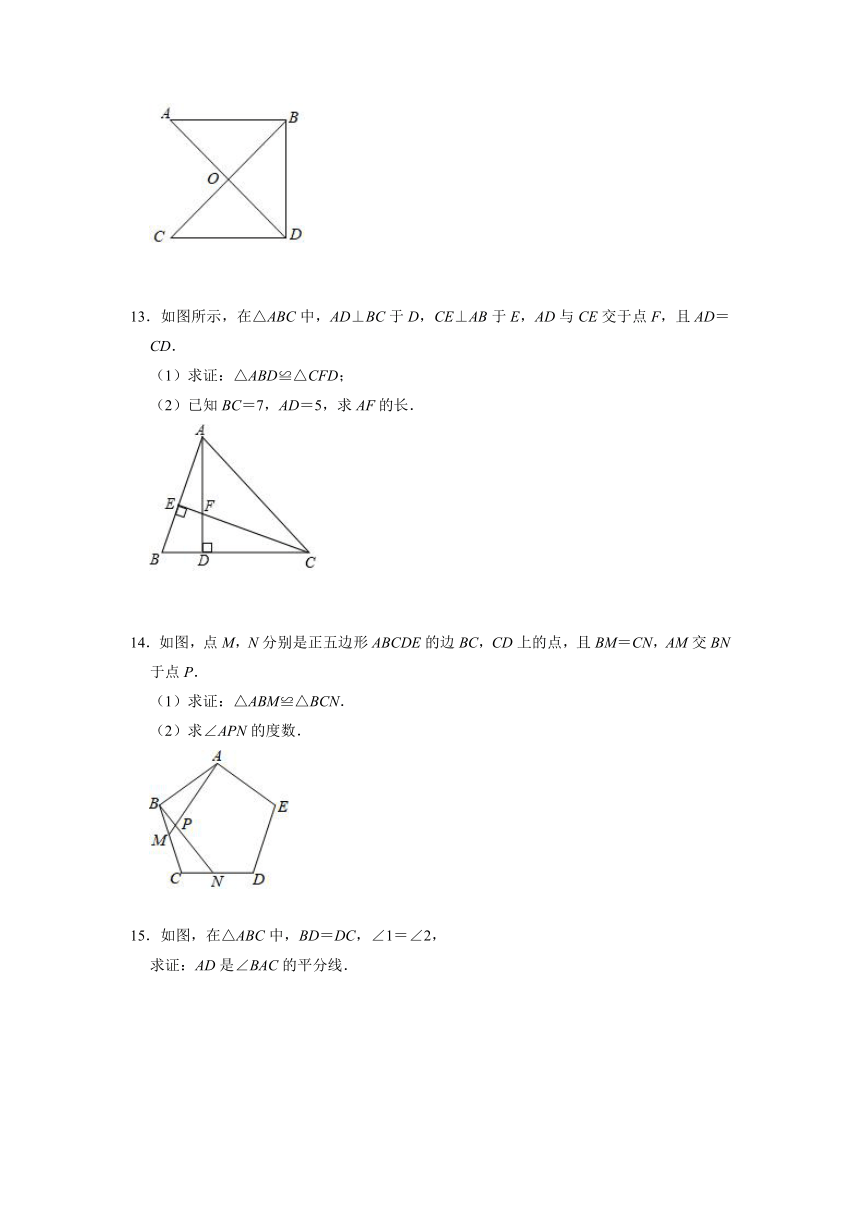
11.如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF=
.
12.已知:AB∥CD,O为AD中点.
(1)请判断△AOB与△DOC是否全等?并说明理由;
(2)若BD=CD,请判断AD与BC的位置关系,并说明理由.
13.如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
14.如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN.
(2)求∠APN的度数.
15.如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
16.在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABC≌△DCB;
(2)当∠AEB=50°时,求∠EBC的度数.
17.如图①点A、B、C、D在同一直线上,AB=CD,作CE⊥AD,BF⊥AD,且AE=DF.
(1)证明:EF平分线段BC;
(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由.
18.如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE,
(1)求证:△ABC≌△ADE;
(2)若AE∥BC,且∠E=∠CAD,求∠C的度数.
19.在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为
;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).
20.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
21.如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,α=90°,则BE
CF;
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件
,使①中的结论仍然成立,并说明理由;
(2)如图3,若线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
参考答案
1.解:∵BC⊥AC,BD⊥AD,AB平分∠CAD,
∴∠ACB=∠ADB=90°,∠CAB=∠DAB,
在△ABC和△ABD中,
,
∴Rt△ABC≌Rt△ABD(AAS),
故选:A.
2.解:∵BC∥EF,
∴∠ACB=∠F,
A.∠B=∠E,BC=EF,∠ACB=∠F,符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
B.AB=DE,BC=EF,∠ACB=∠F,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
C.∵AD=CF,
∴AD+DC=CF+DC,
即AC=DF,
AC=DF,∠B=∠E,BC=EF,∠ACB=∠F,符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;
D.∵AB∥DE,
∴∠A=∠EDF,
∴∠A=∠EDF,∠ACB=∠F,BC=EF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项不符合题意;
故选:B.
3.解:在△ABS与△CBD中,
,
∴△ABS≌△CBD(ASA);
或∵AS∥CD,
∴∠S=∠D.
在△ABS与△CBD中,
,
∴△ABS≌△CBD(AAS);
综上所述,作为证明△SAB≌△DCB的依据的是ASA或AAS.
故选:C.
4.证明:∵CF∥AB,
∴∠1=∠F,∠2=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB﹣AD=9﹣6.5=2.5,
故选:C.
5.解:如图所示:在△GDF与△BGE中,
,
∴△GDF≌△BGE(SAS).
∴S△GDF=S△BEG,
则S阴影=S△EFB=S矩形BCFE.
所以只要知道长方形BCFE的面积即可求得答案.
故选:D.
6.解:在△AEF和△ABC中,
,
∴△AEF≌△ABC(SAS),
∴∠EAF=∠BAC,AF=AC,故②正确
∴∠EAB=∠FAC=40°,故①正确,
∴∠C=∠AFC=∠AFE=70°,
∴∠EFB=180°﹣70°﹣70°=40°,故⑤正确,
∵AE=AB,∠EAB=40°,
∴∠AEB=∠ABE=70°,
若∠EBC=110°,则∠ABC=40°=∠EAB,
∴∠EAB=∠ABC,
∴AE∥BC,显然与题目条件不符,故③错误,
若AD=AC,则∠ADF=∠AFD=70°,
∴∠DAF=40°,这个显然与条件不符,故④错误.
故选:C.
7.解:破玻璃保留了原来三角形的两个角和一边,则可以根据ASA来配一块一样的玻璃,
故选:B.
8.解:∵∠EAC=∠FAB,
∴∠EAB=∠CAF,
在△ABE和△ACF,
,
∴△ABE≌△ACF(AAS),
∴∠B=∠C.AE=AF.
由△AEB≌△AFC知:∠B=∠C,AC=AB;
在△ACN和△ABM,
,
∴△ACN≌△ABM(ASA)(故④正确);
∴CM=BN,
由于条件不足,无法证得②CD=DN;
综上所述,正确的结论是①③④,共有3个.
故选:C.
9.解:如图,延长EB至G,使BE=BG,设AC与DE交于点M,
∵∠ABC=90°,
∴AB⊥GE,
∴AB垂直平分GE,
∴AG=AE,∠GAB=∠BAE=∠DAC,
∵∠BAE=∠GAE,
∴∠GAE=∠CAD,
∴∠GAE+∠EAC=∠CAD+∠EAC,
∴∠GAC=∠EAD,
在△GAC与△EAD中,
,
∴△GAC≌△EAD(SAS),
∴∠G=∠AED,∠ACB=∠ADE,
∴②是正确的;
∵AG=AE,
∴∠G=∠AEG=∠AED,
∴AE平分∠BED,
当∠BAE=∠EAC时,∠AME=∠ABE=90°,则AC⊥DE,
当∠BAE≠∠EAC时,∠AME≠∠ABE,则无法说明AC⊥DE,
∴①是不正确的;
设∠BAE=x,则∠CAD=2x,
∴∠ACD=∠ADC==90°﹣x,
∵AB∥CD,
∴∠BAC=∠ACD=90°﹣x,
∴∠CAE=∠BAC﹣∠EAB=90°﹣x﹣x=90°﹣2x,
∴∠DAE=∠CAE+∠DAC=90°﹣2x+2x=90°,
∴AE⊥AD,
∴③是正确的;
∵△GAC≌△EAD,
∴CG=DE,
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE,
∴④是正确的,
故答案为:②③④.
10.解:①∵∠ACB=45°,BE⊥AC,
∴∠BEA=∠BEC=90°,
∴∠EBD=45°,故①正确;
②∵EH是∠AEB的角平分线,
∴∠HEB=∠AEB=45°,
∴∠HEB=∠EBC=45°,
∴EH∥BC,
∵AD⊥BC,
∴AD⊥EH,
∴EH是AF的垂直平分线,
∴AH=HF;故②正确;
(3)∵∠BDF=90°,∠FBD=45°,
∴∠DFB=45°,
∴DB=DF,
∵∠ACB=45°,AD⊥BC,
∴∠DAC=45°,
∴AD=CD,
在△ABD与△CFD中,
,
∴△ABD≌△CFD(SAS),故③正确;
④∵△ABD≌△CFD,
∴AB=CF,
∴CH=CF+FH=AB+AH;故④正确;
⑤∵DF=AD﹣AF,
∴BD=CD﹣AF.
∵BD=DF+BF,故⑤正确.
综上所述①②③④⑤正确.
故答案为:①②③④⑤.
11.解:∵△ABC≌△DEF,且点B与点E对应,点C与点F对应,
∴BC=EF,
∵BE=5,BF=1,
∴EF=BE﹣BF=4,
∴BC=4,
∴CF=BC﹣BF=4﹣1=3,
故答案为3.
12.解:(1)△AOB与△DOC全等,理由如下:
∵AB∥CD,
∴∠A=∠ODC,
∵O为AD中点.
∴AO=DO,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(ASA);
(2)AD与BC互相垂直,理由如下:
∵△AOB≌△DOC,
∴OB=OC,
∵BD=CD,
∴AD⊥BC.
13.(1)证明:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CDF=∠CEB=90°,
∴∠BAD+∠B=∠FCD+∠B=90°,
∴∠BAD=∠FCD,
在△ABD和CFD中,
,
∴△ABD≌△CFD(ASA),
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
14.证明:(1)∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
,
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°.
即∠APN的度数为108°
15.证明:∵BD=DC,
∴∠DBC=∠DCB,
∵∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD与△ACD中
,
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD是∠BAC的平分线.
16.(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AE=DE,BE=CE,
∴AC=DB,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS);
(2)解:∵△ABC≌△DCB,
∴∠ACB=∠DBC,
∵∠AEB=∠ECB+∠EBC=50°,
∴∠EBC=25°.
17.(1)证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB+BC=BC+CD,即AC=DB,
在Rt△ACE和Rt△DBF中,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC;
(2)(1)中结论成立,理由为:
证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB﹣BC=CD﹣BC,即AC=DB,
在Rt△ACE和Rt△DBF中,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC.
18.解:(1)∵∠1=∠2=∠3,
∴∠1+∠DAC=∠DAC+∠2,即∠BAC=∠DAE,
又∵∠1+∠B=∠ADE+∠3,则可得∠B=∠ADE,
在△ABC和△ADE中
,
∴△ABC≌△ADE(AAS);
(2)∵AE∥BC,
∴∠E=∠3,∠DAE=∠ADB,∠2=∠C,
又∵∠3=∠2=∠1,令∠E=x,
则有:∠DAE=3x+x=4x=∠ADB,
又∵由(1)得
AD=AB,∠E=∠C,
∴∠ABD=4x,
∴在△ABD中有:x+4x+4x=180°,
∴x=20°,
∴∠E=∠C=20°.
19.解:(1)①如图1,∵BA=BC,∠EBD=60°,
∴△ABC是等边三角形,
∴AD=AB=BC,∠DAB=∠ABC=60°,
∴∠EAD=∠FBD=120°,
∵DE=DF,
∴∠E=∠F,
在△AEC与△BCF中,,
∴△ADE≌△BDF(AAS),
∴AE=BF;
故答案为:AE=BF;
②证明:在BE上截取BG=BD,连接DG,
∵∠EBD=60°,BG=BD,
∴△GBD是等边三角形.
同理,△ABC也是等边三角形.
∴AG=CD,
∵DE=DF,∴∠E=∠F.
又∵∠DGB=∠DBG=60°,
∴∠DGE=∠DBF=120°,
在△DGE与△DBF中,,
∴△DGE≌△DBF(AAS),
∴GE=BF,
∴AE=BF+CD;
(2)如图3,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=EG﹣AG;
∴AE=BF﹣CD,
如图4,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=AG﹣EG;
∴AE=CD﹣BF.
20.证明:(1)延长BD交CE于F,
在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠AEC+∠ACE=90°,
∴∠ABD+∠AEC=90°,
∴∠BFE=90°,即EC⊥BD;
(2)延长BD交CE于F,
∵∠BAD+∠CAD=90°,∠CAD+∠EAC=90°,
∴∠BAD=∠EAC,
∵在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABC+∠ACB=90°,
∴∠CBF+∠BCF=∠ABC﹣∠ABD+∠ACB+∠ACE=90°,
∴∠BFC=90°,即EC⊥BD.
21.解:(1)∵∠BEC=∠CFA=α=90°,
∴∠BCE+∠CBE=180°﹣∠BEC=90°.
又∵∠BCA=∠BCE+∠ACF=90°,
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
(2)α+∠BCA=180°,理由如下:
∵∠BEC=∠CFA=α,
∴∠BEF=180°﹣∠BEC=180°﹣α.
又∵∠BEF=∠EBC+∠BCE,
∴∠EBC+∠BCE=180°﹣α.
又∵α+∠BCA=180°,
∴∠BCA=180°﹣α.
∴∠BCA=∠BCE+∠ACF=180°﹣α.
∴∠EBC=∠FCA.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
(3)EF=BE+AF,理由如下:
∵∠BCA=α,
∴∠BCE+∠ACF=180°﹣∠BCA=180°﹣α.
又∵∠BEC=α,
∴∠EBC+∠BCE=180°﹣∠BEC=180°﹣α.
∴∠EBC=∠FCA.
在△BEC和△CFA中,
∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.
∴EF=EC+CF=FA+BE,即EF=BE+AF.
1.如图,BC⊥AC,BD⊥AD,且AB平分∠CAD,则利用( )可说明△ABC与△ABD全等.
A.AAS
B.ASA
C.SAS
D.SSA
2.如图,BC∥EF,BC=EF,要使得△ABC≌△DEF,需要补充的条件不能是( )
A.∠B=∠E
B.AB=DE
C.AD=CF
D.AB∥DE
3.如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.那么C,D两点间的距离就是在A点处小明与游艇的距离.在这个问题中,可作为证明△SAB≌△DCB的依据的是( )
A.SAS或SSS
B.AAS或SSS
C.ASA或AAS
D.ASA或SAS
4.如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6.5,则BD的长为( )
A.1
B.2
C.2.5
D.3
5.如图,正方形ABCD被分割成2个长方形和1个正方形,要求图中阴影部分的面积,只要知道下列图形的面积是( )
A.长方形AEFD
B.长方形BEGH
C.正方形CFGH
D.长方形BCFE
6.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EBC=110°;④AD=AC;⑤∠EFB=40°,正确的个数为( )个.
A.1
B.2
C.3
D.4
7.如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A.SSS
B.ASA
C.SAS
D.HL
8.如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
9.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,点E为BC上一点,连接AE,∠BAE=∠CAD,连接DE.下列结论中正确的是
.(填序号)
①AC⊥DE;
②∠ADE=∠ACB;
③若CD∥AB,则AE⊥AD;
④DE=CE+2BE.
10.如图,在△ABC中,∠ACB=45°,AD⊥BC,BE⊥AC,AD与BE相交于点F,连接并延长CF交AB于点G,∠AEB的平分线交CG的延长线于点H,连接AH,则下列结论:
①∠EBD=45°;②AH=HF;③△ABD≌△CFD;④CH=AB+AH;
⑤BD=CD﹣AF.其中正确的是
.(只填写序号)
11.如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF=
.
12.已知:AB∥CD,O为AD中点.
(1)请判断△AOB与△DOC是否全等?并说明理由;
(2)若BD=CD,请判断AD与BC的位置关系,并说明理由.
13.如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
14.如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN.
(2)求∠APN的度数.
15.如图,在△ABC中,BD=DC,∠1=∠2,
求证:AD是∠BAC的平分线.
16.在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABC≌△DCB;
(2)当∠AEB=50°时,求∠EBC的度数.
17.如图①点A、B、C、D在同一直线上,AB=CD,作CE⊥AD,BF⊥AD,且AE=DF.
(1)证明:EF平分线段BC;
(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由.
18.如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE,
(1)求证:△ABC≌△ADE;
(2)若AE∥BC,且∠E=∠CAD,求∠C的度数.
19.在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为
;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).
20.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
21.如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.
①如图1,若∠BCA=90°,α=90°,则BE
CF;
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件
,使①中的结论仍然成立,并说明理由;
(2)如图3,若线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.
参考答案
1.解:∵BC⊥AC,BD⊥AD,AB平分∠CAD,
∴∠ACB=∠ADB=90°,∠CAB=∠DAB,
在△ABC和△ABD中,
,
∴Rt△ABC≌Rt△ABD(AAS),
故选:A.
2.解:∵BC∥EF,
∴∠ACB=∠F,
A.∠B=∠E,BC=EF,∠ACB=∠F,符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
B.AB=DE,BC=EF,∠ACB=∠F,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
C.∵AD=CF,
∴AD+DC=CF+DC,
即AC=DF,
AC=DF,∠B=∠E,BC=EF,∠ACB=∠F,符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;
D.∵AB∥DE,
∴∠A=∠EDF,
∴∠A=∠EDF,∠ACB=∠F,BC=EF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项不符合题意;
故选:B.
3.解:在△ABS与△CBD中,
,
∴△ABS≌△CBD(ASA);
或∵AS∥CD,
∴∠S=∠D.
在△ABS与△CBD中,
,
∴△ABS≌△CBD(AAS);
综上所述,作为证明△SAB≌△DCB的依据的是ASA或AAS.
故选:C.
4.证明:∵CF∥AB,
∴∠1=∠F,∠2=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB﹣AD=9﹣6.5=2.5,
故选:C.
5.解:如图所示:在△GDF与△BGE中,
,
∴△GDF≌△BGE(SAS).
∴S△GDF=S△BEG,
则S阴影=S△EFB=S矩形BCFE.
所以只要知道长方形BCFE的面积即可求得答案.
故选:D.
6.解:在△AEF和△ABC中,
,
∴△AEF≌△ABC(SAS),
∴∠EAF=∠BAC,AF=AC,故②正确
∴∠EAB=∠FAC=40°,故①正确,
∴∠C=∠AFC=∠AFE=70°,
∴∠EFB=180°﹣70°﹣70°=40°,故⑤正确,
∵AE=AB,∠EAB=40°,
∴∠AEB=∠ABE=70°,
若∠EBC=110°,则∠ABC=40°=∠EAB,
∴∠EAB=∠ABC,
∴AE∥BC,显然与题目条件不符,故③错误,
若AD=AC,则∠ADF=∠AFD=70°,
∴∠DAF=40°,这个显然与条件不符,故④错误.
故选:C.
7.解:破玻璃保留了原来三角形的两个角和一边,则可以根据ASA来配一块一样的玻璃,
故选:B.
8.解:∵∠EAC=∠FAB,
∴∠EAB=∠CAF,
在△ABE和△ACF,
,
∴△ABE≌△ACF(AAS),
∴∠B=∠C.AE=AF.
由△AEB≌△AFC知:∠B=∠C,AC=AB;
在△ACN和△ABM,
,
∴△ACN≌△ABM(ASA)(故④正确);
∴CM=BN,
由于条件不足,无法证得②CD=DN;
综上所述,正确的结论是①③④,共有3个.
故选:C.
9.解:如图,延长EB至G,使BE=BG,设AC与DE交于点M,
∵∠ABC=90°,
∴AB⊥GE,
∴AB垂直平分GE,
∴AG=AE,∠GAB=∠BAE=∠DAC,
∵∠BAE=∠GAE,
∴∠GAE=∠CAD,
∴∠GAE+∠EAC=∠CAD+∠EAC,
∴∠GAC=∠EAD,
在△GAC与△EAD中,
,
∴△GAC≌△EAD(SAS),
∴∠G=∠AED,∠ACB=∠ADE,
∴②是正确的;
∵AG=AE,
∴∠G=∠AEG=∠AED,
∴AE平分∠BED,
当∠BAE=∠EAC时,∠AME=∠ABE=90°,则AC⊥DE,
当∠BAE≠∠EAC时,∠AME≠∠ABE,则无法说明AC⊥DE,
∴①是不正确的;
设∠BAE=x,则∠CAD=2x,
∴∠ACD=∠ADC==90°﹣x,
∵AB∥CD,
∴∠BAC=∠ACD=90°﹣x,
∴∠CAE=∠BAC﹣∠EAB=90°﹣x﹣x=90°﹣2x,
∴∠DAE=∠CAE+∠DAC=90°﹣2x+2x=90°,
∴AE⊥AD,
∴③是正确的;
∵△GAC≌△EAD,
∴CG=DE,
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE,
∴④是正确的,
故答案为:②③④.
10.解:①∵∠ACB=45°,BE⊥AC,
∴∠BEA=∠BEC=90°,
∴∠EBD=45°,故①正确;
②∵EH是∠AEB的角平分线,
∴∠HEB=∠AEB=45°,
∴∠HEB=∠EBC=45°,
∴EH∥BC,
∵AD⊥BC,
∴AD⊥EH,
∴EH是AF的垂直平分线,
∴AH=HF;故②正确;
(3)∵∠BDF=90°,∠FBD=45°,
∴∠DFB=45°,
∴DB=DF,
∵∠ACB=45°,AD⊥BC,
∴∠DAC=45°,
∴AD=CD,
在△ABD与△CFD中,
,
∴△ABD≌△CFD(SAS),故③正确;
④∵△ABD≌△CFD,
∴AB=CF,
∴CH=CF+FH=AB+AH;故④正确;
⑤∵DF=AD﹣AF,
∴BD=CD﹣AF.
∵BD=DF+BF,故⑤正确.
综上所述①②③④⑤正确.
故答案为:①②③④⑤.
11.解:∵△ABC≌△DEF,且点B与点E对应,点C与点F对应,
∴BC=EF,
∵BE=5,BF=1,
∴EF=BE﹣BF=4,
∴BC=4,
∴CF=BC﹣BF=4﹣1=3,
故答案为3.
12.解:(1)△AOB与△DOC全等,理由如下:
∵AB∥CD,
∴∠A=∠ODC,
∵O为AD中点.
∴AO=DO,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(ASA);
(2)AD与BC互相垂直,理由如下:
∵△AOB≌△DOC,
∴OB=OC,
∵BD=CD,
∴AD⊥BC.
13.(1)证明:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CDF=∠CEB=90°,
∴∠BAD+∠B=∠FCD+∠B=90°,
∴∠BAD=∠FCD,
在△ABD和CFD中,
,
∴△ABD≌△CFD(ASA),
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
14.证明:(1)∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
,
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°.
即∠APN的度数为108°
15.证明:∵BD=DC,
∴∠DBC=∠DCB,
∵∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD与△ACD中
,
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD是∠BAC的平分线.
16.(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AE=DE,BE=CE,
∴AC=DB,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS);
(2)解:∵△ABC≌△DCB,
∴∠ACB=∠DBC,
∵∠AEB=∠ECB+∠EBC=50°,
∴∠EBC=25°.
17.(1)证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB+BC=BC+CD,即AC=DB,
在Rt△ACE和Rt△DBF中,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC;
(2)(1)中结论成立,理由为:
证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB﹣BC=CD﹣BC,即AC=DB,
在Rt△ACE和Rt△DBF中,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC.
18.解:(1)∵∠1=∠2=∠3,
∴∠1+∠DAC=∠DAC+∠2,即∠BAC=∠DAE,
又∵∠1+∠B=∠ADE+∠3,则可得∠B=∠ADE,
在△ABC和△ADE中
,
∴△ABC≌△ADE(AAS);
(2)∵AE∥BC,
∴∠E=∠3,∠DAE=∠ADB,∠2=∠C,
又∵∠3=∠2=∠1,令∠E=x,
则有:∠DAE=3x+x=4x=∠ADB,
又∵由(1)得
AD=AB,∠E=∠C,
∴∠ABD=4x,
∴在△ABD中有:x+4x+4x=180°,
∴x=20°,
∴∠E=∠C=20°.
19.解:(1)①如图1,∵BA=BC,∠EBD=60°,
∴△ABC是等边三角形,
∴AD=AB=BC,∠DAB=∠ABC=60°,
∴∠EAD=∠FBD=120°,
∵DE=DF,
∴∠E=∠F,
在△AEC与△BCF中,,
∴△ADE≌△BDF(AAS),
∴AE=BF;
故答案为:AE=BF;
②证明:在BE上截取BG=BD,连接DG,
∵∠EBD=60°,BG=BD,
∴△GBD是等边三角形.
同理,△ABC也是等边三角形.
∴AG=CD,
∵DE=DF,∴∠E=∠F.
又∵∠DGB=∠DBG=60°,
∴∠DGE=∠DBF=120°,
在△DGE与△DBF中,,
∴△DGE≌△DBF(AAS),
∴GE=BF,
∴AE=BF+CD;
(2)如图3,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=EG﹣AG;
∴AE=BF﹣CD,
如图4,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=AG﹣EG;
∴AE=CD﹣BF.
20.证明:(1)延长BD交CE于F,
在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠AEC+∠ACE=90°,
∴∠ABD+∠AEC=90°,
∴∠BFE=90°,即EC⊥BD;
(2)延长BD交CE于F,
∵∠BAD+∠CAD=90°,∠CAD+∠EAC=90°,
∴∠BAD=∠EAC,
∵在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABC+∠ACB=90°,
∴∠CBF+∠BCF=∠ABC﹣∠ABD+∠ACB+∠ACE=90°,
∴∠BFC=90°,即EC⊥BD.
21.解:(1)∵∠BEC=∠CFA=α=90°,
∴∠BCE+∠CBE=180°﹣∠BEC=90°.
又∵∠BCA=∠BCE+∠ACF=90°,
∴∠CBE=∠ACF.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
(2)α+∠BCA=180°,理由如下:
∵∠BEC=∠CFA=α,
∴∠BEF=180°﹣∠BEC=180°﹣α.
又∵∠BEF=∠EBC+∠BCE,
∴∠EBC+∠BCE=180°﹣α.
又∵α+∠BCA=180°,
∴∠BCA=180°﹣α.
∴∠BCA=∠BCE+∠ACF=180°﹣α.
∴∠EBC=∠FCA.
在△BCE和△CAF中,
∴△BCE≌△CAF(AAS).
∴BE=CF.
(3)EF=BE+AF,理由如下:
∵∠BCA=α,
∴∠BCE+∠ACF=180°﹣∠BCA=180°﹣α.
又∵∠BEC=α,
∴∠EBC+∠BCE=180°﹣∠BEC=180°﹣α.
∴∠EBC=∠FCA.
在△BEC和△CFA中,
∴△BEC≌△CFA(AAS).
∴BE=CF,EC=FA.
∴EF=EC+CF=FA+BE,即EF=BE+AF.
